新型准零刚度非线性悬置座椅特性分析与参数匹配

2023-01-16赵雷雷于曰伟曹建虎高尚鹏周长城

中国机械工程 2023年1期

赵雷雷于曰伟曹建虎高尚鹏周长城袁建

1.山东理工大学交通与车辆工程学院，淄博，255000 2.北京北汽越野车研究院有限公司，北京，101300

0 引言

农用车辆、工程车辆等工作环境复杂、路况多变，路面及动力总成激励等引起的振动极易导致车辆及座椅零部件损坏，降低驾乘舒适性[1-3]，损害驾驶员健康[4-6]。目前广泛应用的剪式座椅作为减小车辆振动关键的一环，其悬置隔振性能和使用可靠性显得尤为重要[7]，然而，生产成本在一定程度上制约了其性能提高。如何提高剪式座椅隔振性能和可靠性并降低其生产成本，已成为当前各车企亟待解决的关键问题之一[8-9]。

现有剪式座椅中，传统座椅采用螺旋弹簧作为悬置弹性元件，成本低、可靠性好，但隔振性能较差[10]，其承载能力与隔振效果之间的矛盾难以调和[11-12]。为有效提高传统座椅隔振性能，研究人员从电流变[13]、磁流变[14]等可控阻尼的角度进行了有益探索并在一定程度上提高了座椅振动舒适性，但可控减振器成本高且性能可靠性尚待提高[15]，故应用较少。

准零刚度隔振理论为提高传统座椅性能提供了一条有效路径，目前在理论上已有很多可行方案[16-17]。闫振华等[18]基于线性螺旋弹簧和球面滚子机构设计了非线性悬置座椅；王勇等[19]研究了基于准零刚度隔振器的车-椅-人耦合系统动态特性；DANH等[20]提出了基于气动弹簧负刚度的主动座椅系统。在现有诸多方案中，实际工程应用的依然是传统准零刚度隔振系统，它由一对在垂向产生负刚度的横置线性弹簧、一个垂向放置的线性弹簧并辅之以定位、导向零部件组成[21-22]。然而，实际工程中该类座椅准零刚度结构零部件易失效，如某个横置弹簧失效易导致座椅系统运动不稳定、垂向运动摩擦卡滞等，从而使隔振性能恶化，在极大程度上限制了其推广应用[23-25]。该类座椅推广应用的关键在于保证其隔振性能，优化其隔振拓扑结构并降低复杂性，减少精密零部件种类和数量，建立关键参数匹配理论和快速设计方法，这是降低座椅批量制造成本和提高使用可靠性的有效途径[26]。然而，虽然这种传统非线性座椅隔振性能好且可有效解决线性座椅弊端，但现有研究依然没能有效解决其成本高和可靠性差的问题。

针对现有研究的不足，本文在传统座椅剪式机构基础上增加连杆和辅助弹簧，提出一种新型非线性悬置座椅系统。

1 新型非线性悬置座椅构型与工作原理

1.1 构型

为解决传统线性座椅隔振性能差、非线性座椅成本高且可靠性差的问题，在传统线性座椅剪式机构基础上增加一个垂置副簧和连杆，提出图1a所示新型非线性悬置座椅[26]，其中，剪式机构(由剪杆构成)、线性主簧、减振器等均为传统线性座椅原有组成部分。

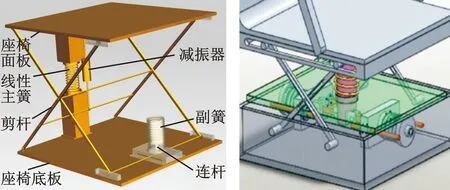
(a)新型非线性悬置座椅 (b)传统非线性悬置座椅图1 准零刚度非线性悬置座椅系统示意图Fig.1 The schematic diagram of the quasi-zero-stiffness nonlinear suspension seat system

图1b所示为传统非线性悬置座椅[27]，主要包括剪式机构、一个垂置弹簧和减振器、两个横置副簧(辅助弹簧)、两个连杆及两套定位零部件。对比可知，新型座椅结构更简单紧凑，比传统结构少用一个辅助弹簧、一个连杆及一套定位零部件，仅在传统线性悬置座椅系统增加副簧和连杆。通过安装/拆除副簧和连杆，可实现传统线性悬置座椅和新型非线性座椅转换，便于工程上实现高低选配。因此，若新型座椅副簧等失效，也能提供传统剪式线性座椅性能，而传统非线性悬置座椅中若一个副簧失效，则易导致性能严重恶化。可见，新型座椅在结构上决定了其成本仅为传统非线性悬置座椅系统的一半且可靠性更高。

1.2 工作原理

新型非线性悬置座椅工作原理如下：座椅负刚度机构由常规剪式机构、连杆及副簧组成，它提供座椅垂向运动导向和负刚度隔振双重功能，主簧提供正刚度，主簧与负刚度机构的共同作用使座椅悬置系统垂向变形与弹性回复力关系曲线的中间呈较长平直段，两侧呈现强非线性特性。在驾乘人员重力作用下，主簧与副簧发生压缩变形，连杆运动至与座椅底板相垂直位置。车辆受振动激励时，悬置系统由静平衡位置开始发生压缩和复原运动，连杆在垂直位置发生左右摆动，协同减振器的阻尼作用，隔离低频振动。其中，当悬置系统发生压缩运动时，主簧的压缩量增大，副簧的压缩量减小；当悬置系统发生复原运动时，主簧的压缩量减小，副簧的压缩量增大，即在不同工作位置时主簧与副簧始终协同工作。

主簧与副簧的协同作用可实现高静态刚度和低动态刚度。在静平衡位置时，新型悬置系统的垂向动刚度接近于零。当座椅在静平衡位置附近振动时，新型悬置系统动刚度低于传统线性悬置系统动刚度，可有效衰减座椅垂向振动，此时，新型悬置系统呈现高静态刚度特性，静态刚度大于传统线性悬置系统静刚度，可实现较好静态承载。当远离静平衡位置时，新型悬置系统具有强动刚度且大于传统线性悬置系统动刚度，可较好地限制座椅大幅度振动，实现悬置系统限位，有效避免极限工况下座椅悬置撞击现象。此外，在剪杆与座椅底板之间安装橡胶防撞块，也可避免撞击现象。

2 新型非线性悬置座椅系统建模

2.1 物理模型

图2所示为图1a中新型非线性悬置座椅系统的简化物理模型。设座椅整体坐标系Oxyz原点与座椅初始位置时剪杆与底板上导轨铰接点S重合，x轴水平向前，z轴垂直向上。设PS=QR=L，AS=a，BR=r，BQ=c。座椅初始位置时，剪杆PS与SR夹角为θ0。在载荷作用下，剪杆PS与SR夹角为θ。座椅初始位置及任意位置各点坐标如表1所示。初始位置几何尺寸如图2所示。

图2 座椅系统力学模型示意图Fig.2 The schematic diagram of mechanical model of the seat system

表1 座椅在初始位置及任意位置时各点的坐标Tab.1 The coordinates of each point of the seat at the initial position and at any position

2.2 数学模型

2.2.1力-位移静力学建模

如图2所示，座椅初始位置时，设辅助弹簧上下安装点间距为l0，则高度h0可表示为

(1)

若座椅面板由初始位置产生向下位移u，点P移动到P′点。根据几何关系可知

zP0-zP=u

(2)

将zP=Lsinθ及zP0=Lsinθ0代入式(2)，可得

Lsinθ0-Lsinθ=u

(3)

由式(3)，可得

sinθ0-u/L=sinθ

(4)

若座椅面板由初始位置产生向下位移量u，则此时B点坐标zB表示为

(5)

此时，R点坐标xR表示为

(6)

将式(6)代入式(5)，可得

zB=

(7)

辅助弹簧由初始位置发生变形后，其安装点之间距离

l=zA-zB=l0+h0-

(8)

若座椅面板由初始位置产生向下位移u，则辅助弹簧变形量

Δl=l0-l=

(9)

采用螺旋弹簧作为辅助弹簧，则其任意位置弹性压缩力

Fs=Ks(l0-l)=Ks·

(10)

式中，Ks为辅助弹簧刚度。

在座椅系统中撤去主弹簧，则当辅助弹簧弹性力为Fs时，座椅面板所受外力记为Fn，根据虚功原理，可得

Fnδu-Fsδ(Δl)=0

(11)

根据式(9)～式(11)，虚位移δ(Δl)及负刚度机构垂向力Fn的解析表达式分别为

(12)

Fn=

(13)

在座椅系统中，若主弹簧采用螺旋弹簧且考虑其预变形量u0，则当座椅面板产生位移u时，其弹性力

Fp=Kv(u+u0)

(14)

式中，Kv为主弹簧刚度。

座椅系统中主弹簧和辅助弹簧产生的总垂向弹性力Ft可表示为

Ft=Fp+Fn

(15)

将式(13)及式(14)代入式(15)，可得总垂向弹性力Ft的解析表达式。

2.2.2力-刚度建模

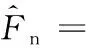
(16)

为满足座椅隔振及人机工程需求，在座椅剪式负刚度机构设计时，需基于座椅额定载荷匹配合理的座椅悬置垂向变形ue及剪杆与座椅底板夹角θe，故需将式(16)中参数γ1和γ2用ue和θe表示。根据几何关系，可得

(17)

(18)

由式(18)，可得

(19)

将(18)代入式(19)，可得

(20)

2.2.3座椅系统动力学建模

新型座椅系统采用液压减振器，其阻尼力Fc可表示为[28]

(21)

式中，C0为减振器线性阻尼系数；v1f、v1r分别为减振器复原和压缩初次开阀速度；v2f、v2r分别为减振器复原和压缩二次开阀速度；γf、γr分别为复原和压缩比例系数；vt为减振器相对运动速度。

设座椅在自身和驾驶员总有效质量m作用下，主弹簧产生垂向变形ue后达到静平衡位置。设座椅垂向位移激励为q，座椅面垂向位移为z。将Ft中变量u替换为ue-(z-q)并加mg，可得座椅系统以静平衡位置为零点的整体垂向弹性回复力Fte表达式。根据牛顿第二定律，座椅系统振动微分方程为

(22)

3 新型非线性悬置座椅系统特性分析

3.1 可变承载特性分析

座椅系统承载特性直接影响其隔振性能。驾驶员重量变化可能恶化悬置隔振性能，故需对新型悬置座椅系统的承载特性进行分析。图1a所示的新型悬置座椅系统参数如下：Kv=20 N/mm，Ks=50 N/mm，θ0=49°，β0=36°，L=600 mm，r=40 mm。在u0依次取值0，5，10，15 mm的情况下，根据式(15)，总垂向弹性力Ft随相对位移u的变化曲线如图3所示。

图3 总垂向弹性力Ft随相对位移u的变化曲线Fig.3 The curve of the vertical elastic restoring force Ft vs. the displacement u

图3中曲线中间呈现较长平直段，两侧呈现强非线性特性，其中，平直段对应的Ft值表征座椅系统静态承载能力。当主簧预变形量u0增大时，Ft值随之增大，悬置可承载的有效质量依次为60，70，80，90 kg。可见，新型悬置座椅系统可通过主簧3的安装来调节其预变形量u0，以适应不同体重的驾驶员。

3.2 负刚度机构静力学特性分析

表2 量纲一变量的取值范围Tab.2 The value range of the dimensionless variables

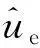
对的影响

对的影响图4 不同取值时和随变化曲线Fig.4 The curves of and vs. different values of

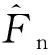
(a)γ2e对的影响

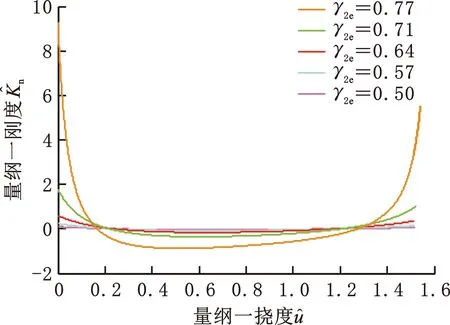
(b)γ2e对的影响图5 不同γ2e取值时和随变化曲线Fig.5 The curves of and vs. at different values of γ2e

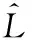
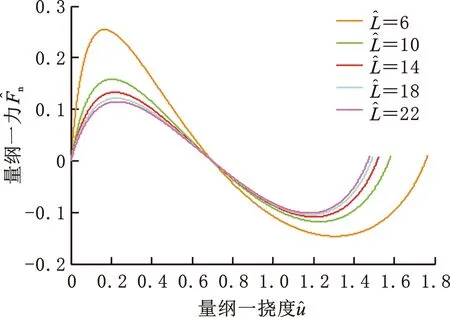
对的影响

对的影响图6 不同取值时和随变化曲线Fig.6 The curves of and vs. at different values of

3.3 低频振动传递特性分析

新型座椅系统是一个强非线性振动系统，故本文采用正弦扫频方法进行精确求解。基于所建座椅系统动力学模型，在正弦幅值A0分别为3，7，11 mm三种情况下进行扫频仿真。其中，扫频间隔为0.02 Hz，扫频区间为0.1～5.0 Hz，仿真时间设置为120 s。计算每个频率下加速度稳态输出与输入幅值比值，得悬置系统加速度传递率T。图7所示为减振器线性阻尼系数C0=500 N·s/m时不同激振强度下的传递率曲线，图8所示为A0=3 mm时不同C0值下的传递率曲线。

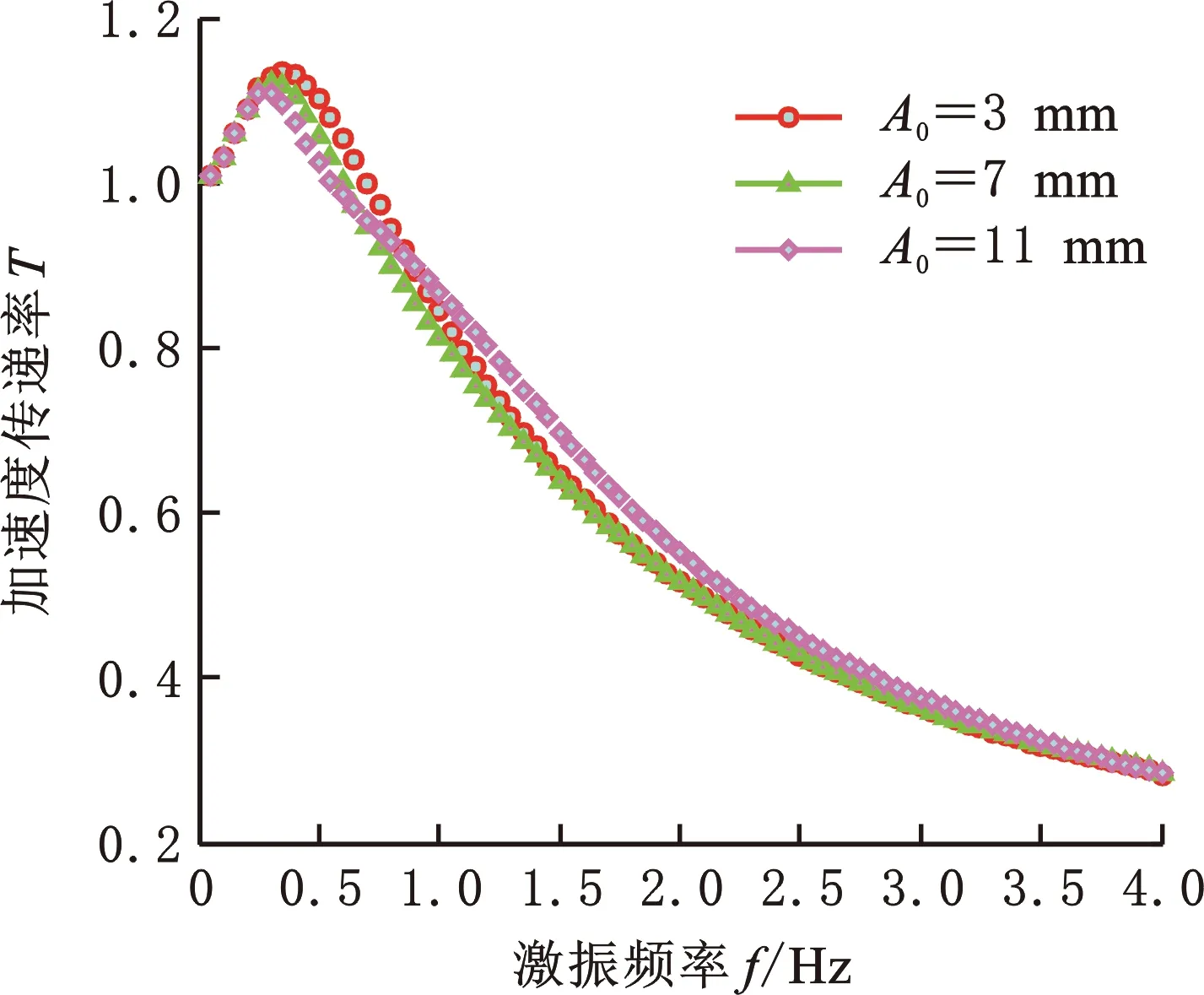
图7 不同A0时传递率T对比Fig.7 A comparison of the transmissibility T at different A0

图8 不同C0时传递率T对比Fig.8 A comparison of the transmissibility T at different C0

由图7可知，当C0=500 N·s/m时，不同激振强度下座椅加速度传递率T在0.3～2 Hz低频区内差异较为明显，其他区域差异较小。可见，激励幅值A0对系统振动传递特性在低频区影响较大。分析图8可知，C0=300 N·s/m时，T曲线有两个峰值。第一个在0～0.5 Hz范围内，峰值较小；第二个在1～2 Hz范围内，峰值较大且发生共振频率转移现象，导致系统不稳定。这是由新型悬置座椅系统非线性较强且在静平衡点两侧刚度不完全对称而造成的。进一步分析可知，随着C0值增大，第二个共振峰消失；C0值越大，第一个共振峰值越小，但在非共振区T值明显增大。综上，C0值不宜过小或过大。

4 非线性悬置刚度与阻尼优化匹配

在探明新型座椅系统特性影响规律基础上，建立悬置刚度与阻尼匹配模型并进行实例设计。

4.1 刚度解析匹配模型

4.1.1悬置主弹簧刚度参数匹配

根据座椅承载有效质量m及静平衡位置时座椅悬置垂向变形量ue，确定新型悬置座椅系统主簧刚度Kv设计值，即

Kv=mg/ue

(23)

Kv值根据质量m额定值确定(此时主弹簧预变形量u0=0)，通过调节主弹簧预变形量u0，可满足其他质量需求。例如，某驾驶员乘坐后，m比额定值大Δm，则主弹簧预变形量u0可调整为u0=Δmg/Kv。

4.1.2悬置副弹簧刚度参数匹配

主弹簧刚度Kv确定之后，副弹簧刚度Ks将由座椅结构参数、额定载荷位置要求、主簧刚度Kv及等效垂向刚度Ke共同确定。

已知ue和L，根据式(4)，剪杆与座椅底板初始夹角

θ0=arcsin(sinθe+ue/L)

(24)

确定θ0后，根据式(1)，连杆与座椅底板初始夹角

β0=arcsin(h0/r)=

(25)

对前述整体垂向弹性回复力Fte表达式求相对位移u的导数，得等效垂向刚度Ke表达式，即

(26)

式中，χ1、χ2、χ3、χ4均为u的函数表达式。

将式(26)变形并令u=0，则χ1、χ2、χ3、χ4均确定且Kv、θ0及β0已知，此时副簧刚度

(27)

其中，Ke由额定载荷m下静平衡位置座椅系统要求固有频率f0确定。

4.2 阻尼匹配数学模型

4.2.1评价指标及其计算方法

根据ISO2631标准，采用座椅面垂向加权加速度均方根aw评价座椅舒适性，其计算式如下：

(28)

滤波网络W(f)用如下传递函数实现[29]，即

(29)

4.2.2阻尼匹配数学模型构建

为提高座椅振动舒适性，以座椅减振器阻尼参数X(X=(C0，v1f，v1r，γf，γr))为优化设计变量，以aw最小为优化目标，建立目标函数：

(30)

式中，Ω为X设计域。

为避免车辆行驶过程中座椅面与其导轨撞击，须满足概率约束条件[30]：

(31)

式中，fd为座椅悬置动挠度；[fd]为座椅悬置限位行程，[fd]=0.03 m；σ(fd)为fd的均方根。

基于目标函数J及约束条件，新型悬置座椅系统阻尼参数匹配数学模型为

(32)

上述数学问题属于有约束优化问题，可基于文献[30]提供的流程，采用全局优化算法求解，如遗传算法、粒子群算法等。

4.3 参数匹配设计实例

为提高某4×2农用车驾乘舒适性[30]，根据额定载荷65 kg下静平衡位置座椅系固有频率0.3 Hz及行驶路况要求，为该试验车辆配置了新型非线性悬置座椅系统并进行了样机试制。具体设计如下：根据座椅安装空间要求和结构参数对负刚度机构静力学特性影响规律，得额定载荷下静平衡时主簧变形设计值ue=30 mm、剪杆长度L=600 mm、连杆长度r=40 mm。根据刚度解析匹配数学模型，得剪杆与座椅底板初始夹角θ0=49°，连杆与底板初始夹角β0=36°，主簧刚度Kv=20 N/mm、副簧刚度Ks=50 N/mm。基于所建座椅系统动力学模型，以文献[30]实测砂石路况下试验车辆座椅底板垂向振动加速度为输入，利用减振器阻尼匹配方法进行参数匹配，结果为：C0=756 N·s/m，v1f=0.11 m/s，v1r=0.09 m/s，γf=0.71，γr=0.62。加工得到图9所示的试验样机。其中，主簧采用线性螺旋弹簧TF50；副簧为线性螺旋弹簧TF40；主簧可调安装座采用Q235螺纹铁管，用于调整主簧预紧变形量u0；连杆采用关节轴承SA12T/K；滚轮采用滚针轴承CF10/KR22。

图9 试验样机Fig.9 The test prototype

5 试验验证与能效分析

为验证所建理论模型和参数匹配方法的正确性并检验新型悬置座椅的隔振能力和效果，下文进行了静力学、扫频及随机振动试验对比分析。

5.1 静力学试验对比分析

试验设备为长春试验机研究所生产的30 kN综合试验台，如图10所示，该试验台可自动进行数据采集和试验数据打印。试验之前，拆除减振器并在各运动副涂润滑油，将座椅面板与试验台架横梁固定，将座椅底板与试验台架的作动器固定；随后，通过作动器加载并跑合20次，取最后一次数据为最终试验结果。加载速度对试验结果影响较大，而本试验主要目的是测试静态力下位移-力关系，因此，试验过程中加载速度设定为5.0 mm/min。试验测试结果对比如图11所示。

图10 座椅静力学试验Fig.10 seat static test

图11 位移-力曲线对比Fig.11 Ft-u curve comparison

由图11可知，u-Ft试验曲线与理论设计曲线平直段吻合较好，其他部分存有一定差异。对比结果表明，所建新型悬置座椅位移-力静力学模型能够较好地反映悬置系统真实静力学特性。曲线存有差异主要是运动副存在间隙和干摩擦且试验样机加工尺寸有一定偏差所致。此外，因干摩擦导致卸载试验曲线呈现滞回现象。

5.2 扫频试验对比分析

用65 kg配重代替驾驶员并固定在新型座椅面上，在综合试验台施加幅值为6.0 mm的正弦激励以进行扫频试验；然后，拆除副簧和连杆，将新型座椅转换为传统剪式线性机械座椅并进行扫频试验。其中，扫频间隔为0.05 Hz，扫频区间为0.1～6 Hz。图12所示为加速度传递率试验与仿真对比曲线。

图12 加速度传递率试验与仿真曲线对比Fig.12 A comparison of T curves between the test and the simulation

由图12可知，新型座椅加速度传递率仿真与试验曲线吻合较好，两者在0～4 Hz几乎重合，仅在4～6 Hz略有差异。结果验证了所建新型座椅系统动力学模型的正确性。与传统剪式线性机械座椅相比，新型座椅最大传递率和固有频率分别降低了31.2%和80.6%，对比结果表明新型座椅隔振性能明显优于线性座椅。

此外，因试验中线性座椅由新型座椅拆除副簧而来，拆除副簧后负刚度机构摩擦力几乎消失，故线性座椅T试验曲线比新型座椅的更光滑。对比结果也说明，新型座椅若副簧失效，可提供传统剪式线性座椅隔振性能，确保性能不严重恶化，从而提高新型悬置座椅系统实用性和可靠性。

5.3 随机振动试验对比分析

为进一步对比验证新型非线性座椅减振性能，将前期试验所测砂石和沥青两种路况下座椅底板加速度转换为位移信号[30]，以此驱动综合试验台作动器，分别对新型非线性座椅、传统非线性座椅及传统线性座椅施加振动激励，进行随机振动试验，如图13所示。同时，为对比分析非线性悬置座椅系统失效情况下隔振性能，将新型非线性座椅副簧拆除，将传统非线性座椅其中一侧副簧拆除，复现实际工程中最常见失效形式并分别进行试验。试验之前拆除各座垫，消除坐垫对座椅性能对比的干扰。沥青路况下新型非线性座椅垂向加速度试验与仿真时间历程对比如图14所示，不同座椅垂向加权加速度均方根aw及悬置动挠度均方根σ对比如表3所示。

图13 随机振动试验Fig.13 The random test

图14 加速度对比Fig.14 Acceleration comparison

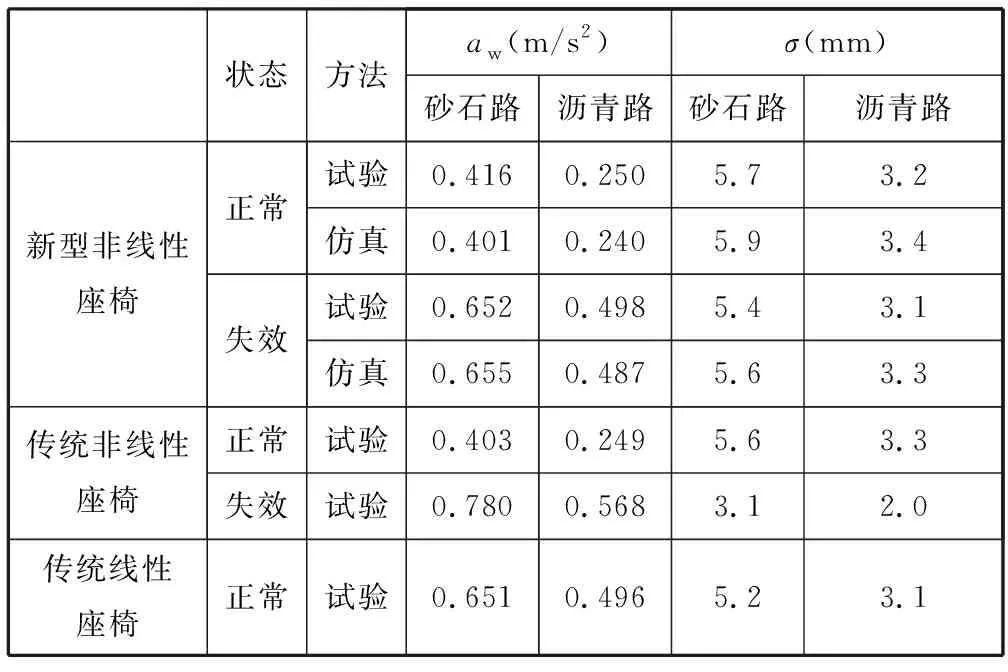
表3 座椅减振性能对比Tab.3 A comparison of the seat performance

由图14可知，沥青路况下新型非线性座椅垂向加速度试验与仿真时间历程吻合较好，表明所建座椅系统动力学模型能有效复现座椅在随机路况下的真实动力学响应。分析表3可知，砂石和沥青两种路况下新型非线性座椅垂向加权加速度均方根aw仿真值与试验值相对偏差分别为3.6%和4.0%，悬置动挠度均方根σ仿真值和试验值相对偏差分别为3.5%和6.3%，对比结果进一步验证了所建动力学模型的正确性。误差主要是由所建座椅系统动力学模型没有考虑运动副摩擦和间隙造成的。

进一步分析表3可知，正常工作状态下，两种路况下新型非线性座椅的σ值和aw值与传统非线性座椅的相当；与传统线性座椅相比，虽然新型非线性座椅的σ值略有增大，但砂石和沥青路况下aw值分别降低了36.0%和49.6%。在失效状态下，与传统线性座椅相比，两种路况下传统非线性的aw值分别增大了19.8%和14.5%，而新型非线性座椅的σ值仅分别增大了0.2%和0.4%。可见，正常工作下新型非线性座椅减振性能与传统非线性座椅相当，但失效状态下新型非线性座椅减振性能与传统线性座椅相当，且明显优于传统非线性座椅。进一步分析可知，因失效状态下，新型非线性座椅转化为了传统线性座椅，故其性能没有严重恶化；而传统非线性座椅在横置副簧侧向力作用下导致座椅垂向运动产生一定卡滞，故σ值明显减小且aw值增大。

综上分析，与传统线性座椅相比，新型非线性座椅振动舒适性显著提高且与传统非线性座椅相当；与传统非线性座椅相比，新型非线性座椅不仅结构简单、成本低、便于工程上实现高低选配，而且使用可靠性更高。