一种结构解耦型变刚度驱动软体手抓握能力分析
2023-01-16尹海斌
尹海斌 陶 鉴 李 骞 周 佳
1.数字制造湖北省重点实验室,武汉,430070 2.武汉理工大学机电工程学院,武汉,430070
0 引言
机器人要完成预定的工作任务,一般需要一个末端执行器(机械手),从这点上来讲,大量应用于机器人技术中的机械手具有重要的作用。然而,现有的大多数机械手主要是针对特定作业环境和操作对象而设计的刚性机械手,缺乏适应性和安全性[1],不能满足机器人高性能的需求。软体机械手的研究符合新一代机器人技术的发展趋势,具有重要的科学价值和意义。
但是,也正是因为软体机械手容易变形而存在刚度不足或出力不够的问题。为充分利用软体机械手的适应性优点,需研究其刚度不足等问题的解决方法,因此,研究软体机械手的变刚度驱动原理或方法具有重要的科学意义和工程实践的价值。国内外学者对软体机械手的变刚度驱动进行了大量的针对性研究。查阅已发表的文献,根据变刚度与变形驱动的实现方式可归纳为如下4类:
(1)不对称受力变形驱动。该类研究的特点是软体由在不对称结构或不对称作用力(统称“不对称受力”)下产生的变形驱动。LOW等[2]研究了气压驱动的非对称结构软体手指抓握物体的情况,指出多根软体手指将物体缠绕可以抓紧一定重量物体。王超[3]采用电机收放绳索产生不对称力,驱动仿象鼻软体产生弯曲变形。气体驱动需要泵站打压,绳驱动需要电机拖放,这些方法存在整体驱动功率密度低的问题。李健等[4]研究了形状记忆合金(SMA)直接电驱的仿象鼻软体机械手,指出SMA具有较大驱动力,提高了软体机械手的驱动功率密度。不对称受力可变形驱动软体,但实际中的软体机械手还需要刚度可变,以适应不同的环境。
(2)对称受力变形驱动与变刚度。这类机构的特点是不仅可以变形驱动还可以变刚度驱动。当对称力作用于变结构时,它属于等张力变形驱动;当对称力作用于不变结构时,它属于等长变刚度。上述两种情况统称为拮抗控制[5]。第一种情况与流体驱动的非对称结构弯曲变形本质上是一致的,但拮抗控制中的变形驱动是可逆的,能让关节在对称中心两边一定范围内转动。手指关节不需要对称驱动,因此,为了提高驱动材料变形的利用率,软体手指关节的驱动控制一般不用拮抗控制方式。拮抗控制的第二种情况可以帮助理解变刚度的方法,理解如下:当流体压力作用于一个对称的软体型腔时,压力的调整可以改变软体型腔的刚度。如HART等[6]在柔软的纤维内嵌入SMA,并通过调整SMA张力来控制纤维刚度,这一方法中,SMA的长度基本不变,整个纤维体结构没有变化,属于等长调整张力变刚度。
(3)材料特性变刚度。除了调整软体材料内的张力可以控制其刚度外,还可以通过调整材料内其他特性来实现刚度控制。PETTERSSON等[7]利用磁场能作用软体内磁流变液体介质使其黏度可调的原理,设计了软体刚度可控的机械手爪。SHINTAKE等[8]针对受热的低熔点合金可在固态与液态之间转变的机理,研究了介电弹性体与低熔点合金组合的可变刚度软体驱动器(VSDEA)。另外,还有一种广泛应用的形状记忆高分子(SMP)材料,通过控制温度改变材料内部相组织来调节控制刚度[9]。YAMANO等[10]利用形状记忆凝胶(SMG)构建了变刚度的软体机器人结构,通过改变SMG材料的相组织来实现刚度控制。这些低熔点金属或凝固态物质可以实现变刚度控制,具有结构简单紧凑、功率密度大的优点,但是它们存在拉伸强度不够的问题,因此,利用这类材料时通常需要其他材料作为封装固化环境。上述纤维内嵌SMA中通过张力调整实现变刚度其实也是通过材料的相组织变化导致弹性模量的变化来实现结构刚度变化,其中SMA具有很高的拉伸强度。只有变刚度结构,不能形成驱动,需考虑变刚度机构与变形驱动的配合。
(4)解耦型变刚度与变形驱动。利用独立的材料结构实现变形驱动和变刚度控制,它们在结构上是独立解耦的,组合后可以实现变刚度与变形驱动,被称为结构解耦型变刚度与变形驱动。实现变刚度与变形驱动的方式有多种,所以组合成结构解耦型变刚度驱动控制方法也有多种。HAO等[11]采用气动肌肉与低熔点合金分别实现变形驱动与变刚度控制,设计了一款变刚度软体手;WEI等[12]采用气动肌肉与SMP实现了软体手的变刚度抓取。这些方法虽然在结构上解耦实现了变刚度与变形驱动,但是气动肌肉在变形驱动时会伴随产生微小的刚度变化。LI等[13]采用两种SMA材料分别实现了软体手指的变刚度与变形驱动,驱动特性与刚度特性在结构上是完全解耦的。
上述文献只研究了材料的力学特性,初步设计了相应软体手指的实验装置,实现了变刚度驱动。目前需要进一步研究增大变刚度范围的其他拓扑结构,也需要进一步研究软体机械手变刚度驱动系统的设计方法和对应的抓握能力。
1 手指指尖力模型
图1是软体手指尖抓握物体的示意图与任一手指的坐标图。软体手的受力状态在三维空间中进行描述:三根手指沿Y轴方向上的摩擦力共同承担指尖所抓握物体的重力,在抓握平面上三根手指指尖对所抓握物体表面的正压力矢量之和为0。根据力平衡原理,抓握操作可以描述为

(a)指尖抓握示意图 (b)任一手指坐标图图1 软体手指尖抓取Fig.1 Fingertip grasping of soft hand
(1)
(2)
式中,Fmg为被抓物体的重力;FYi、FXi为第i个手指分别受到的Y向和X向作用力。
式(2)表示抓握时多个手指水平方向分力应满足力封闭条件。满足该条件时,能抓握起来的物体重力Fmg为软体手的抓握力。
对于第i个手指,如果被抓物体表面在与手指指间接触点处的法线与X轴平行,那么,FXi是指尖力,由滑动摩擦知,FYi=μFXi。如果被抓物体表面在与手指接触点处的法线与X轴成φ角,那么,FNi是指尖力,由滑动摩擦知,Ffi=μFNi,且FXi=FNisinφ-μFNicosφ,FYi=FNicosφ+μFNi·sinφ。由此可知,只要能够确定接触点的指尖力及摩擦因数,手指的抓握力就可以确定。
1.1 手指指尖力模型
为了计算手指的指尖力,需要给定被抓物体表面曲线方程H(X,Y)。在力矩Td的作用下,手指与物体接触产生的指尖力与X轴平行,这个过程可建立指尖力模型。
图2所示为软体手指的坐标系,OXY是与底座固定的全局坐标系,oxy是手指中任一点的局部坐标系。手指中任一点由参数s表征,表示o点到O点的未伸长度。手指上任一点在全局坐标系中表示为r(s),附在手指任一点的局部坐标oxy相对全局坐标OXY旋转了角度θ(s)。根据运动学可知:
r′(s)=(sinθ,cosθ)T
(3)
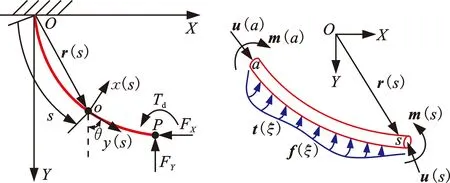
(a)手指整体受力图 (b)局部受力、力矩图图2 坐标系内的手指受力、力矩图Fig.2 Force and moment balance of finger in coordinate system
如图2b所示,从a到s的一段手指中任一点的位置变量为ξ,任一点的集中力和力矩表示为u和m,该段手指上的分布力和力矩记为f和t。由力和力矩平衡,可得静力学方程:
u′(s)+f(s)=0
(4)
m′(s)+r′(s)×u(s)+t(s)=0
(5)
手指不受分布力矩作用,t=0,考虑任一点的弯矩与角度的关系,可得本构方程:
m(s)=EIθ′(s)
(6)
式中,EI为等效刚度。
手指重力为分布力,记f(ξ)=(0,-ρAgξ)(ρ为等效密度;A为等效横截面积;g为重力加速度)。手指与物体接触力为集中力u(L)=[FXFY],由式(4)可得
(7)
式中,L为手指长度。
由式(3)~式(7)可得
(8)
为了求解上述微分方程,给定边界条件如下:
(9)
式中,Fd为软体手指的驱动力;hSMA为软体手指与软体手指骨架中性面的距离。
在手指弯曲力矩作用下,可以计算手指的弯曲变形和抓握时的受力情况,包括手指指尖力FX。
1.2 手指指尖力实验结果分析
手指的具体结构及材料参数参考文献[14],此外,手指参数中等效密度ρ、等效横截面积A以及等效刚度EI如表1所示,由已知的手指结构参数即可计算指尖力。为了验证上述理论模型与计算结果的正确性,实验测试了手指指尖力。实验平台及原理如图3所示。根据SMA-3驱动规律通电,SMA-3纤维的弹性模量24,37,47 GPa对应通电电流分别为0,0.7,1.0 A。SMA-2纤维U形嵌入手指的外一端固定在传感器1上,通电会收缩变形。两个力传感器分别测量指尖力FX和驱动力Fd。

表1 结构参数与材料参数Tab.1 Structural and material parameters

(a)实验装置 (b)实验原理图3 指尖力实验Fig.3 Experimental of fingertip force
手指长度L应为关节间距lSMA的整数倍,因此当手指长度为80 mm且末端发生接触时,手指与接触物体在X方向的距离为30 mm时手指指尖力的计算结果如图4所示。在刚度一定时,指尖力随着驱动力的增大而增大;最大指尖力随着刚度的增加而增大。仿真计算结果显示,SMA-3的弹性模量E3从24 GPa增大到47 GPa,最大指尖力从0.65 N增大到0.98N,增大了50.8%。

图4 变长度的双股和四股SMA-2纤维驱动手指指尖力结果Fig.4 Results of grasping force of finger actuated by two-ply fiber and four-ply fiber with various SMA-2 length
图4中的离散点数据为实验测试数据。由于SMA-2纤维的应变小于4%,故需要足够的纤维长度才能获得足够的变形来驱动手指弯曲。如图4所示,前面三个图分别采用了三种不同长度的驱动纤维,驱动纤维的长度增大能够增大手指的抓握力,但是驱动纤维长度增大到一定极限(1000 mm)后,手指的抓握力不会再继续增大;手指最大的抓握力保持在0.65 N左右,不能体现变刚度的作用。这是因为驱动纤维的收缩变形量不仅与长度有关,还与其负载有关。为了进一步增大手指的抓握力,采用双U形SMA-2纤维嵌入手指,降低每根纤维的负载,保证它足够的收缩变形。图4中后面两个图的实验数据显示,多股纤维驱动能够进一步增大手指抓握力。当采用双U形驱动纤维的长度为1000 mm时,E3=47 GPa下的手指最大的抓握力增大到0.8 N;当其长度增大到1100 mm时,E3=37 GPa下的手指最大的抓握力能达0.98 N,而且抓握力的测试数据变得更加容易分辨。这说明多股驱动纤维不仅可以提高驱动能力,而且能够将驱动力的非线性变得更加平缓,易于分辨与测试。
手指抓握力实验能够发现理论预测的规律,而且能够证明理论模型和计算具有一定的预测精度。本文基于手指抓握力模型对软体手的结构进行设计并对抓握力进行研究。
2 软体手结构设计
本文设计的软体手具有三根手指,其整体结构如图5所示。每根手指由球形指甲、支架、变刚度骨架SMA-3和驱动SMA-2组成[14]。软体手最上端为手掌,手掌左侧布置了两根长度为L1且结构相同的小指,小指之间的距离e=40 mm,右侧布置了一根长度为L2的大指。小指和大指与Y轴正向的夹角分别为θ1和θ2,其延长线交于Q点,夹角满足β=θ1+θ2。以小指的指根位置建立平面坐标系原点O,那么大指的指根位置坐标为P(XP,YP),而交点Q与大指、小指之间的距离LQO、LQP可表示为

(a)正视图 (b)侧视图图5 软体手的设计模型Fig.5 Designed model of soft robot hand
(10)
由式(10)可知,XP、YP、θ1、θ2这4个参数值可用于描述软体手的整体结构尺寸,其中XP定为50 mm。
图6所示为软体手指尖力作用点与驱动力之间的关系,手指在自然伸长状态a时,当受到驱动力Fd1时刚好发生接触,如b,此时指尖力为0,作用点位置为Y1,当增大驱动力,手指继续弯曲,指尖向上滑动,如c,不断增大驱动力,直到手指脱离接触,可得到一组FXi与Yi之间的对应模型,该模型同样可由式(8)和式(9)给出。图7所示为大小手指长度分别为100 mm和80 mm,倾角θ1、θ2均为25°时一组指尖力位置关系。在手指SMA-3纤维刚度从24 GPa到47 GPa之间变化时,小指的抓取域U1和大指的抓取域U2可定义为

图6 软体手指指尖力作用点与驱动力变化关系Fig.6 Relationship between torque and action point
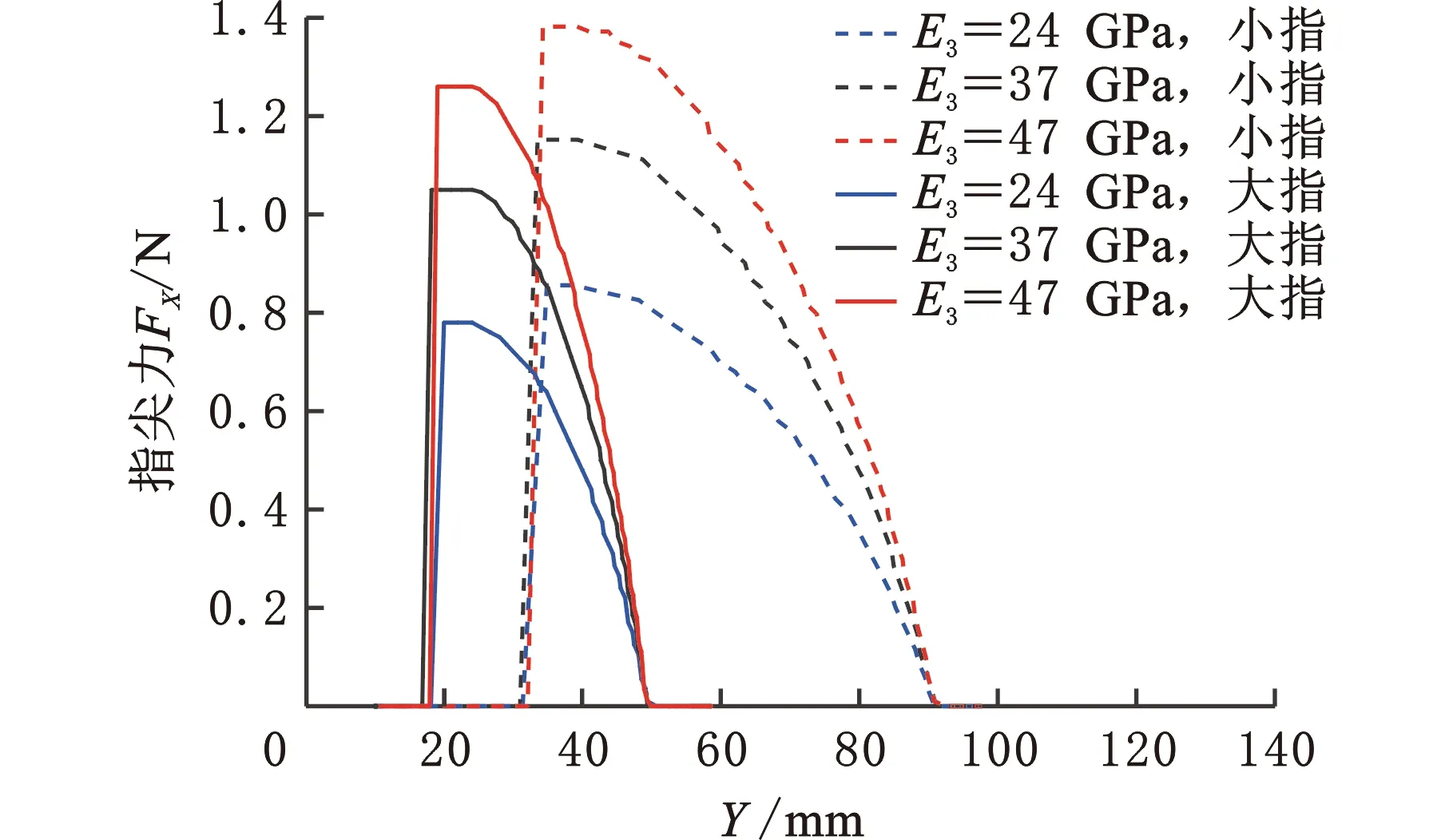
图7 指尖力与作用点关系Fig.7 Relationship between fingertip force and action point

(11)

(12)
式中,Fds1为E3=47 GPa时小指的驱动力;Fds2为E3=24 GPa时小指的驱动力;Fdb1为E3=47 GPa时大指的驱动力;Fdb2为E3=24 GPa时大指的驱动力。
U1和U2的重合度越好,抓取软体手力学性能越强,重合度T可定义为
由前面的分析可知,软体手系统设计的要素在于强化软体手抓握性能,也就是重合度T。在边界条件的设置下通过迭代优化得到全局最大重合度及此重合度下的设计变量最优值。设计变量需考虑大小手指的长度以及手指与手掌间的夹角,另外还考虑了手指与手掌的位置关系,因此设计变量为
(L1,L2,θ1,θ2,YP)
(13)
优化目标为
submax=T{L1,L2,θ1,θ2,YP}
(14)
结合实际进行分析,软体手的设计过程中还需要满足以下要求:①大指抓握力约为小指的2倍(力封闭);②θ1+θ2为45°左右(仿人手结构);③考虑驱动性能的限制,大指的指尖力不大于1.2 N(驱动力限制);④手指长度均为20 mm的整数倍,且实际长度不宜偏离人手指过多。将以上要求通过数学式表达为
(15)
图8为优化计算的流程图,初始条件下大指小指长度均为60 mm、倾角为0°,计算此时的手指抓握域并判断指尖力是否分别满足FN1≤1.2 N,FN2≤1.2 N,不满足时增大倾角θ1,当θ1增大时指尖力逐渐减小。满足条件后再判断是否均满足条件|FN1-2FN2|<0.1 N,40°≤θ1+θ2≤50°。当同时满足以上约束条件时,经过优化调整,计算得到此时的重合度T并与记录的TM进行比较,更替更大的T并记录此时的手指选型。不满足时不断更替小指的倾斜角θ2以及长度,计算所有小指可能的情况之后,对大指进行重新迭代,直到计算所有情况并得到最大重合度T。

图8 优化计算流程图Fig.8 Optimization flow chart
将流程图编入到MATLAB程序中进行计算,得到重合度T的迭代结果,如图9a所示,对应的最优指尖力模型如图9b所示。10次迭代计算之后重合度取最大值0.954,此时小指的长度为100 mm,倾斜角θ1=35°,大指长度为80 mm,倾斜角θ2=15°,大指指根沿着Y正方向移动11 mm,即P点坐标为(50,11)mm,LQP和LQO分别为62 mm和59.6 mm。依据图5所示模型及优化结果,制作了图9c所示的软体手样机。
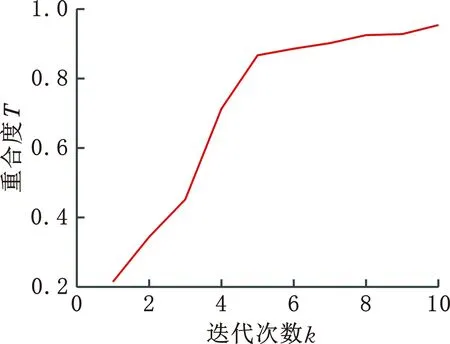
(a)最大重合度计算

(b)指尖力最优模型

(c)软体手样机图9 优化结果Fig.9 Optimization result
软体手样机的驱动SMA-2通电收缩,软体手指相应弯曲,实现包裹物体而抓取,由于不同重量物体需要不同抓握力,故还需要软体手的变刚度骨架SMA-3在通电状态下实现变刚度,这样软体手就能够实现变刚度抓取。
3 软体手的抓握力
图10为指腹抓取的抓握力示意图,当手指腹部与截面为圆形、质量为mg的被抓物体接触时,接触面产生指向圆心的正压力FN(下标L表示小指,R为大指)以及与正压力垂直的摩擦力Ff,所有手指正压力与摩擦力在垂直方向分力的合力即为抓握力Fg,抓握力与物体重力平衡。与指尖力接触相比,指腹抓取的抓握力同时受到正压力和摩擦力的影响,因此数值上会更大,此外其接触形式也更加复杂,这导致传统的分析方法难以预测指腹抓握力大小,本文选用ABAQUS软件对抓握力进行建模分析。
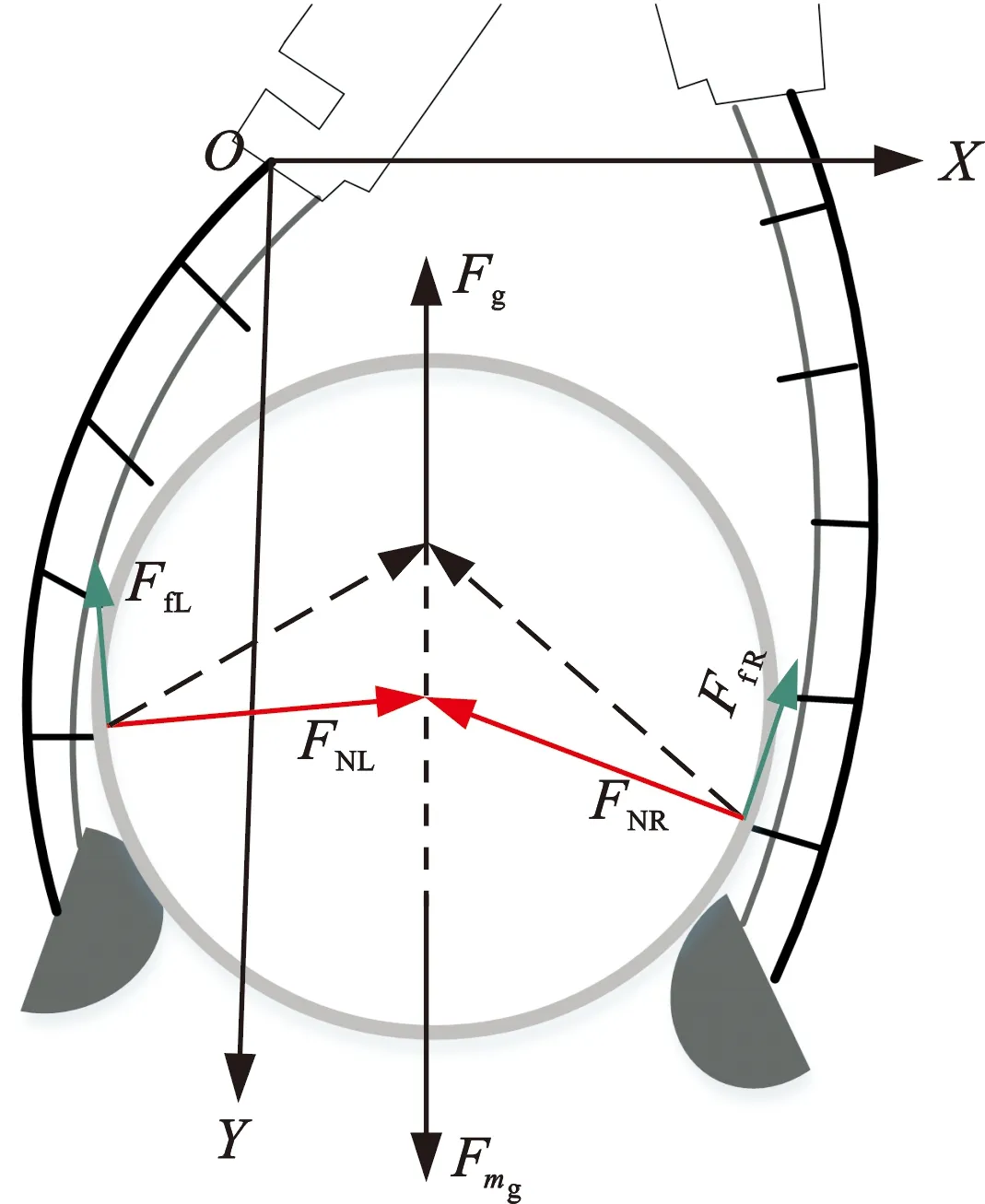
图10 指腹抓取示意图Fig.10 Grasping of finger pulp
3.1 抓握力仿真分析
在对抓握力进行仿真分析之前,首先对仿真变量进行确定。除等效刚度EI和驱动力Fd会对抓握力产生较大影响外,被抓物体在Y方向移动过程中,接触表面的变化也会导致抓握力的改变,因此被抓物体Y方向位置的变化量ΔY也是仿真变量。
与指尖力一致,分别选取E=24,37,47 GPa进行仿真。对于驱动力的选择,由于图4中的指尖力实验结果中单股驱动SMA长度1000 mm时驱动力不超过5 N,因此驱动力矩Td的最大值不应超过40 N·mm。表2所示为仿真中刚度和驱动力的具体对照关系。三组刚度下纵向比较驱动力存在一个4 N·mm的梯度差,这可以使驱动力的仿真具有一个更大的对比范围。

表2 仿真力矩参数Tab.2 Torque parameters of simulation
将手指简化成弹性杆,并根据表1中的软体手指尺寸参数计算其等效刚度。被抓物体圆形坐标P在Y方向不同位置的仿真结果如图11所示,被抓物体为直径60 mm的壳体,其圆心坐标为(25 mm,Yi),Yi表示被抓物体在Y方向变化。在图11a中,被抓物体上表面刚好不与手掌接触,此时圆心坐标为(25,34)mm,图11d中,被抓物体刚好与手指不脱离,此时圆心坐标为(25,94)mm,图11b和图11c则为Y=54 mm和Y=74 mm时的中间状态。从Y=34 mm到Y=94 mm之间,依据2 mm的间隔一共被分为31等份计算其抓握力,得到被抓物体从Y=34 mm到Y=94 mm移动过程中抓握力变化关系,如图12所示。

(a)Y=34 mm (b)Y=54 mm (c)Y=74 mm (d)Y=94 mm图11 抓握力仿真Fig.11 Simulation of grasp force
(a)E=24 GPa
(b)E=37 GPa

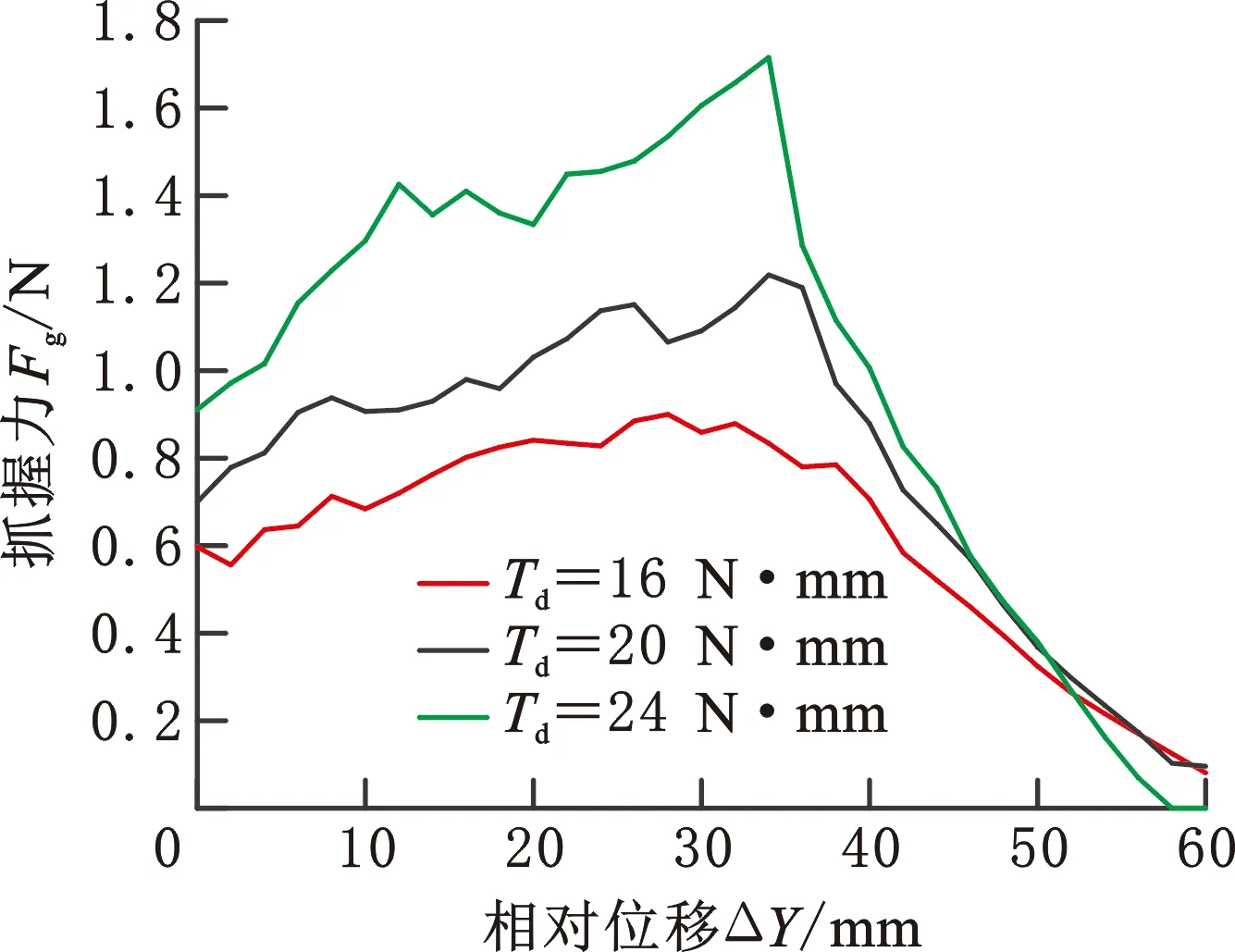
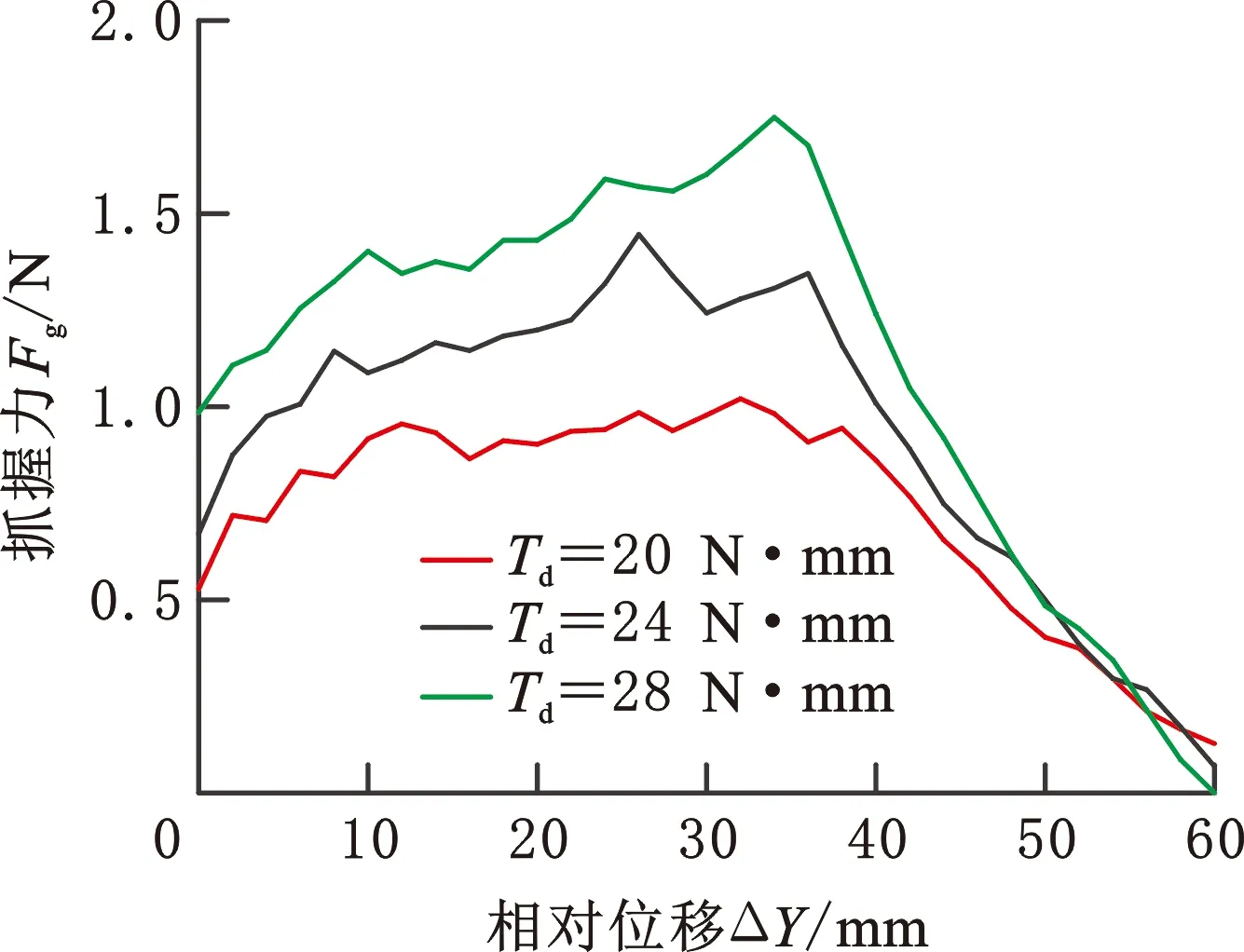
(c)E=47 GPa图12 软体手抓握力模型Fig.12 Grasp force model of soft hand
图12中,摩擦因数为实际测得,统一取0.35。ΔY=0即Y=34 mm时的仿真点,ΔY从0~60 mm变化用于描述Y从34~94 mm的过程。在三种不同刚度下,抓取力均呈先增大后减小的趋势。ΔY在30 mm附近时达到最大值1.716 N、1.75 N和1.895 N,之后逐渐降低到0,当刚度增大时,驱动力对抓握力的增幅减小,但手指刚度大时手指承受较大驱动力时不会发生变形。
3.2 抓握力实验
图13所示为验证指腹抓握力模型正确性所设计的实验平台。在手指结构内部,三根手指的驱动SMA-2丝末端均与1 kg量程的驱动力传感器相连接,通过PID控制驱动电流的大小对传感器测量的驱动力进行反馈控制。抓握力的测量则通过布置在软体手上端和被抓物体下端的抓握力传感器1和抓握力传感器2实现,本实验中,软体手和抓握力传感器1固定在实验平台上方,在测量过程中始终保持恒定。被抓物体和测力传感器2固定在垂直位移计上,通过调节垂直位移计可以控制被抓物体垂直向下缓慢匀速移动。以软体手小指的指根O为坐标系原点,被抓物体中心坐标(X,Y)沿着Y轴移动时,可以通过抓握力传感器测量此时软体手的抓握力和位移计测量对应的位移值。图14所示为抓握状态与相对位移的关系,其中相对位移0,20,40,60 mm分别对应Y轴的34,54,74,94 mm。

(a)实验原理 (b)实验装置图13 抓握力测量实验Fig.13 Experimental for grasping force measurement

(a)ΔY=0 (b)ΔY= (c)ΔY= (d)ΔY= 20 mm 40 mm 60 mm图14 抓握状态与相对位移关系Fig.14 Relationship between grasping state and relative displacement
由于抓握力传感器1测量时存在一个较大的初始值(软体手自重),而抓握力传感器2在测量过程中被抓物体的波动会影响传感器测量精度,且传感器1和传感器2测量的对象为一组支反力,因此可以通过同时比较传感器1和传感器2的测量结果来判断实验测量的准确性,图15所示为手指SMA-3丝刚度为37 GPa、驱动力矩为28 N·mm时的测量结果,两个传感器的最大差异为0.03 N。

图15 传感器测量结果对比Fig.15 Comparison of sensor measurement results
在图16所示的仿真模型中,每组刚度分别选取一组对应下的驱动力矩,调节实验装置中的位移计,使被抓物体圆心从Y=34 mm到Y=94 mm之间移动,得到三组仿真与实验的对照结果。抓握力实验测量与仿真结果仅在ΔY=30 mm附近吻合,并且在ΔY>30 mm时误差恒定。分析认为这种恒定的误差形式来自于摩擦力,即仿真中摩擦力为动摩擦,而实际中,其摩擦形式为静摩擦甚至无摩擦,从而导致实验测得的抓握力普遍小于仿真值。

(a)E=24 GPa,Td=16 N·mm
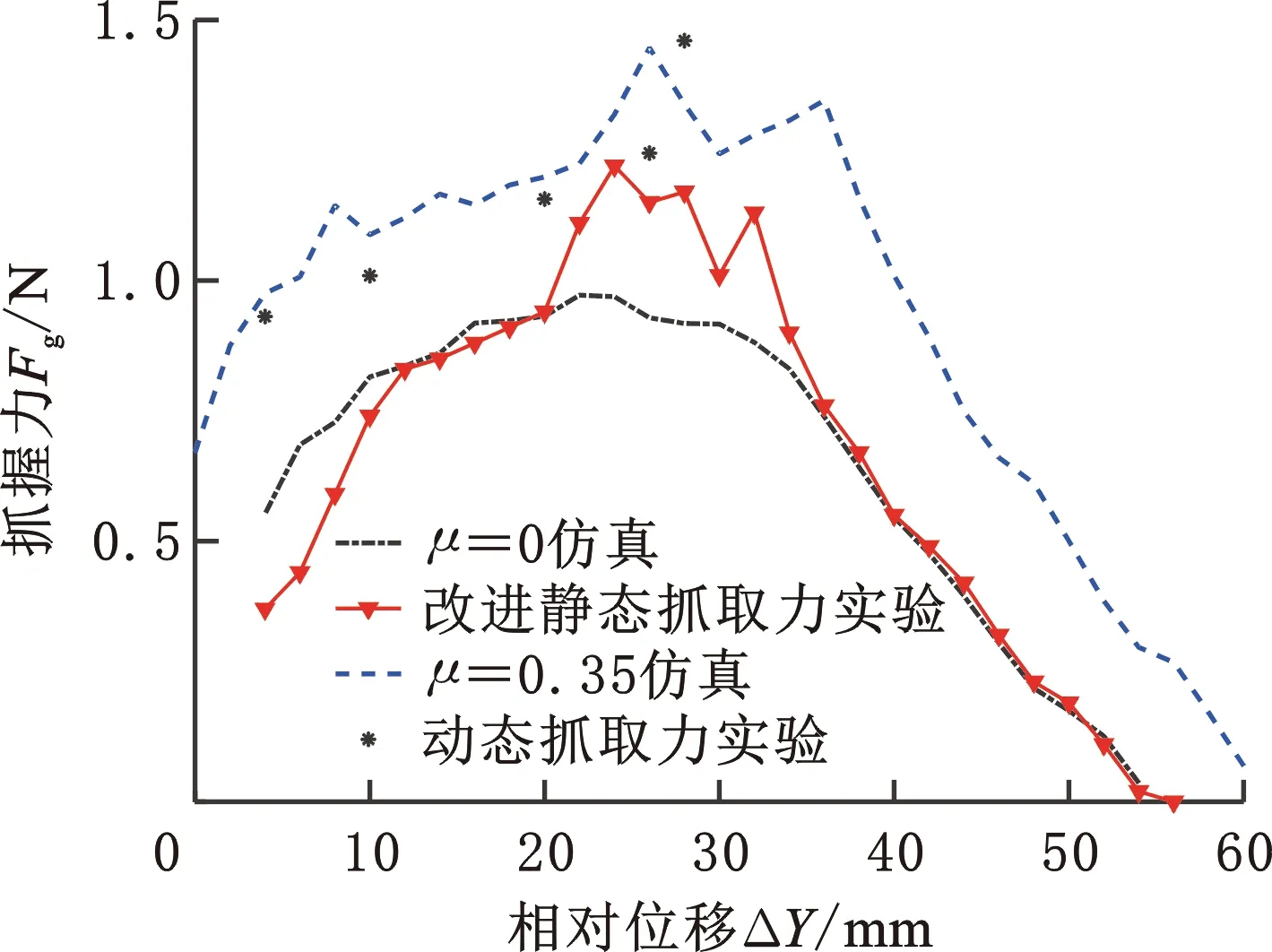
(b)E=37 GPa,Td=24 N·mm

(c)E=47 GPa,Td=32 N·mm图16 仿真与实验结果对比Fig.16 Comparison of simulation and experiment
基于以上猜想,本文进行了一组摩擦因数μ=0的抓握力仿真,如图16所示,实验中抓握力和μ=0仿真在ΔY>30 mm区间吻合。这表明:当ΔY>30 mm时,软体手的抓取形式为手指头和圆柱物体的面接触,此时为无摩擦模型;当ΔY≤30 mm时,软体手的抓取形式为指腹的包裹抓取,其抓取力为指腹和圆柱体贴合处产生的分布力,此时接触力为无摩擦或微量摩擦。整体来看,实验测量的抓握力在指腹抓取和指尖抓取时摩擦力均很小,而在两种抓取状态切换时,摩擦力急剧增大,最大可与μ=0.35模型吻合。实验结果与μ=0以及μ=0.35模型的贴合可以证明μ=0仿真模型的准确性,但是在实际抓取过程中,软体手和被抓物体之间存在相对运动,μ=0.35仿真模型能否预测此时抓握力的大小还需进一步验证。图16中的离散点即为动态抓取的验证结果,其原理如图17a所示,图17b所示为其中质量为mi时的抓取状态。首先给被抓物体一定质量m1,将它放在ΔY=0的位置,通电时缓慢放落,待被抓物体被抓紧时测量其坠落位移ΔY1,之后在图17b所示的被抓物体蜂巢中添加螺钉以增加质量Δm,被抓物体继续下落,待它稳定时测量此时的位移ΔY2,依次增加被抓物体质量,直到软体手无法承托,被抓物体脱离。将被抓物体质量换算为抓握力,图16中的动态抓取离散点分布在μ=0.35仿真中的ΔY<30 mm区间,从而验证μ=0.35 模型的正确性。

(a)实验原理 (b)实验平台图17 动态抓取实验Fig.17 Dynamic grasping experiment
4 结论
本文设计了一款变刚度软体手指并研究了其驱动力与指尖力之间的关系,并针对驱动力不足的问题对SMA的驱动性能进行了研究,得到了SMA 的指尖力模型。根据指尖力模型对软体手抓的结构进行了优化设计,使软体手在指尖抓取时各手指具有最大的抓取重合度。最后针对更加复杂的指腹包裹抓取,本文通过ABAQUS软件进行仿真分析,通过静态抓握力测量实验以及动态抓握实验进行验证,并将实验得到的结果和μ=0、μ=0.35两组仿真模型进行对比。其中,静态实验和μ=0.35模型的对比结果表明仿真与实验的误差主要来自于摩擦力的处理以及实验原理等的影响,静态改进实验表明实验结果基于无摩擦模型,动态抓握实验证实了软体手抓握力和μ=0.35模型相符。
研究得出,当刚度一定时指尖力随着驱动力的增大而增大,当刚度增加时最大指尖力会随着刚度的增大而增大。
