矮塔斜拉桥墩高对摩擦摆支座隔震性能的影响研究

2023-01-16王富强季日臣夏修身

公路工程 2022年6期

王富强，季日臣，夏修身

(兰州交通大学土木工程学院，甘肃兰州 730070)

0 引言

近年来矮塔斜拉桥在工程建设中越来越常见，相比较于梁桥，它的跨越能力更大、外形更加优美，这使得矮塔斜拉桥在未来有很大的发展空间[1]。在大中跨桥梁的建设中，矮塔斜拉桥受到了众多设计者的青睐。

在我国西部地区，地震活动比较频繁，随着西部交通运输的不断发展，桥梁抗震必将成为该地区的技术难题。如何提高桥梁的抗震性能成为迫在眉睫的问题。在2008年汶川地震以后，国内开始大力发展减隔震技术[2]。桥梁的减隔震技术主要是运用减隔震装置隔绝地面运动对桥梁的破坏，进而保护桥梁安全工作[3]。减隔震支座在实际工程中运用广泛，其中摩擦摆支座就是之一，其工作原理是延长结构周期从而减小地震对结构的影响[4]。摩擦摆支座的使用，不仅减小了地震对桥梁的影响，而且使不同桥墩的内力平均[5]。不过在一些学者的研究中发现随着桥梁墩高的变化，摩擦摆支座的减隔效果也会发生变化。王黎园等[6]发现，随着墩高的增加，墩顶变形和支座变形的比值也增加。王建强等[7]发现，运用隔震支座，桥墩高度的变化对桥墩的内力影响较大，对主梁的影响较小。田玉文等[8]研究了在不同桥墩高度下的连续刚构桥抗震性能，结果显示一个桥墩高度的增加会使较矮的桥墩底和主梁根部的内力值最大。吴迪等[9]发现墩高对桥梁的隔震性能有一定的影响，在桥墩矮时影响较大，随着桥墩变高，影响程度呈下降趋势。陈克坚等[10]分析了在不同支座情况下铁路简支梁桥的模型，进而得到了各个桥墩的位移和内力，确定了这种桥型在使用隔震支座时适用的桥墩高度范围。KARIM等[11]发现，当桥墩高度较高时，桥梁在地震下会更容易被破坏。肖章权[12]通过研究不对称高墩大跨度连续刚构桥，得到结论，随着桥墩高度的不断增加，桥梁在各个方向的刚度都减小了。本文以(100+168+100)m的靖远金滩黄河大桥主桥为背景，使用Midas/Civil软件建立在不同墩高下的模型。在实际情况下，随着墩高的增加，桥梁各个结构都会随之变化，本文为了定性研究墩高对矮塔斜拉桥摩擦摆减隔震支座的影响，假定桥梁其他参数保持不变，桥墩高度变化，分析设置摩擦摆支座矮塔斜拉桥的隔震效果。

1 工程背景

靖远金滩黄河大桥主桥(100+168+100)m为三跨变截面矮塔斜拉桥，主梁为单箱五室预应力混凝土箱梁，采用C55混凝土。桥面宽度为36.5 m，支点梁高为7 m，跨中梁高为3.3 m，箱梁底板下缘按1.8次抛物线变化。7#墩与8#墩支座的曲率半径为9 m，正常工况下的摩擦系数为0.03，地震工况下的摩擦系数为0.05，主墩竖向设计承载力边支座为80 000 kN，中支座为200 000 kN，主墩地震起始力边支座为6 000 kN，中支座为15 000 kN，减隔震位移为300 mm。其中支座构造图如图1所示。桥墩采用C40混凝土，横桥向设置三肢实体墩身，墩高为7#桥墩、8#桥墩15 m，承台高为5 m，承台底布置12根1.8 m的桩基础，桩长35 m。通过地勘报告得到桥址处地震动峰值加速度为0.20g，相应的地震烈度为Ⅷ度，地震动加速度反应谱特征周期为0.45 s。其中摩擦摆支座构造图见图1，桥型布置图见图2，主墩横断面图见图3。

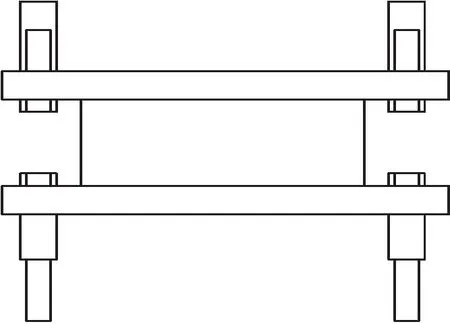
图1 摩擦摆支座构造图

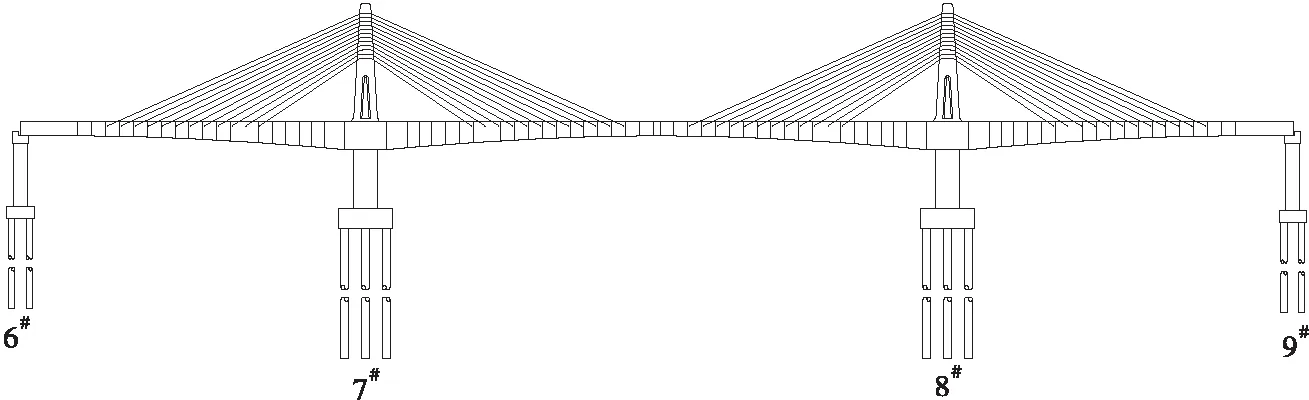
图2 桥型布置图

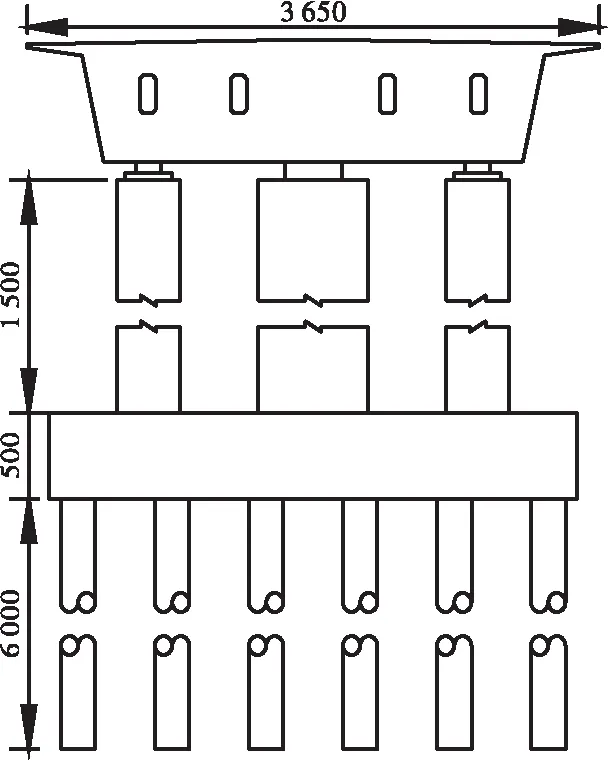
图3 主墩横断面图

2 有限元模型

在有限元建模时，分别建立4种墩高变化的隔震桥梁模型和4种相应的非隔震桥梁模型。本文主要研究8#桥墩中肢的内力和位移，桥墩高度变化分别为：工况一15 m；工况二20 m；工况三25 m；工况四30 m。

本文使用Midas/Civil建模软件来进行数值模拟计算。主梁用弹性梁单元模拟。摩擦摆支座的模拟用一般连接特性中的内力型，在一般连接单元分析中，根据非线性的特性计算出来的内力置换成外部荷载，间接的考虑非线性。其中7#墩中支座X，Y，Z方向的有效刚度为108kN/m，边支座X，Z方向的有效刚度为108kN/m，Y方向为22 220 kN/m；8#墩中支座X，Y方向的有效刚度为108kN/m，Z方向为55 500 kN/m，边支座X方向有效刚度为108kN/m，Y，Z方向为22 220 kN/m。摩擦摆支座的功能是延长结构的基本周期，减小桥梁结构的地震响应，桥墩处于线弹性状态，采用弹性梁单元模拟。桩基模拟采用梁单元模拟，桩土效应通过“土弹簧”模拟。在非隔震桥梁中除了支座采用一般支座，用一般支撑模拟，其他构件模拟都与隔震桥梁相同。图4为实际工程下的有限元模型。

图4 有限元模型

3 地震动输入

本桥型选用的地震波是根据进行过桥址安全性评价的评估报告给出的3条地震波，依据规范要求将3条地震波中对桥梁影响最大的一条地震波选取出来，通过计算对每个方向的地震波放大系数进行调整。最终本文选取了Elcent地震波，地震波从X、Y方向输入。用非线性动力时程分析方法，比较分析不同工况下主桥结构的地震响应。图5是波形时程函数图。

图5 Elcent 波时程函数图

4 结果分析

4.1 自振频率

为了对比在不同墩高下的矮塔斜拉桥自振频率的变化规律，分别对本文的4个工况采用多重Ritz向量法进行动力特性的研究。选取了4个工况的前五阶自振特性结果。自振特性前五阶结果见表1～表4。

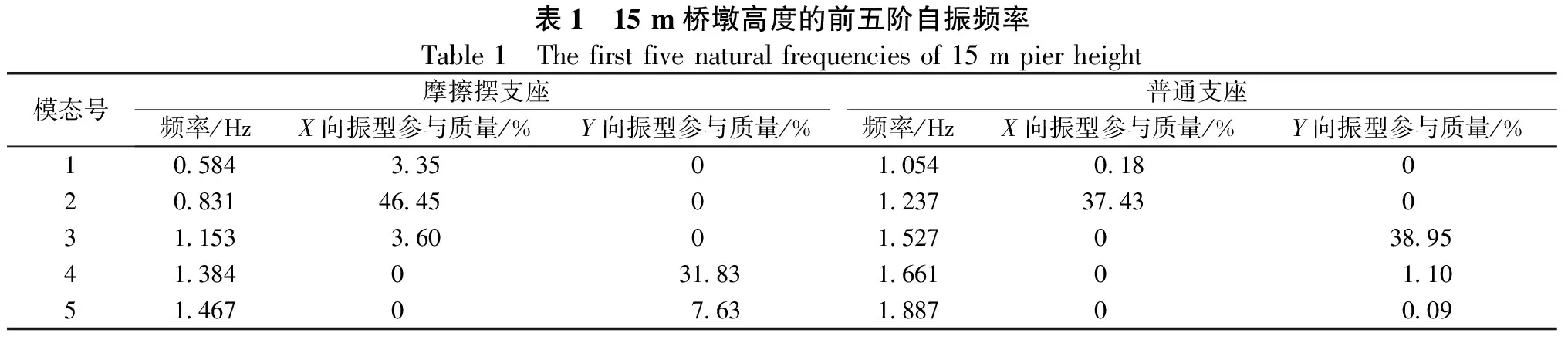
表1 15 m桥墩高度的前五阶自振频率Table 1 The first five natural frequencies of 15 m pier height模态号摩擦摆支座普通支座频率/HzX向振型参与质量/%Y向振型参与质量/%频率/HzX向振型参与质量/%Y向振型参与质量/%10.5843.3501.0540.18020.83146.4501.23737.43031.1533.6001.527038.9541.384031.831.66101.1051.46707.631.88700.09

表2 20 m桥墩高度的前五阶自振频率Table 2 The first five natural frequencies of 20 m pier height模态号摩擦摆支座普通支座频率/HzX向振型参与质量/%Y向振型参与质量/%频率/HzX向振型参与质量/%Y向振型参与质量/%10.57511.6201.0180.42020.67440.4401.13745.07031.132046.941.321046.7741.1330.7801.53000.8251.2700.003.451.85200.27

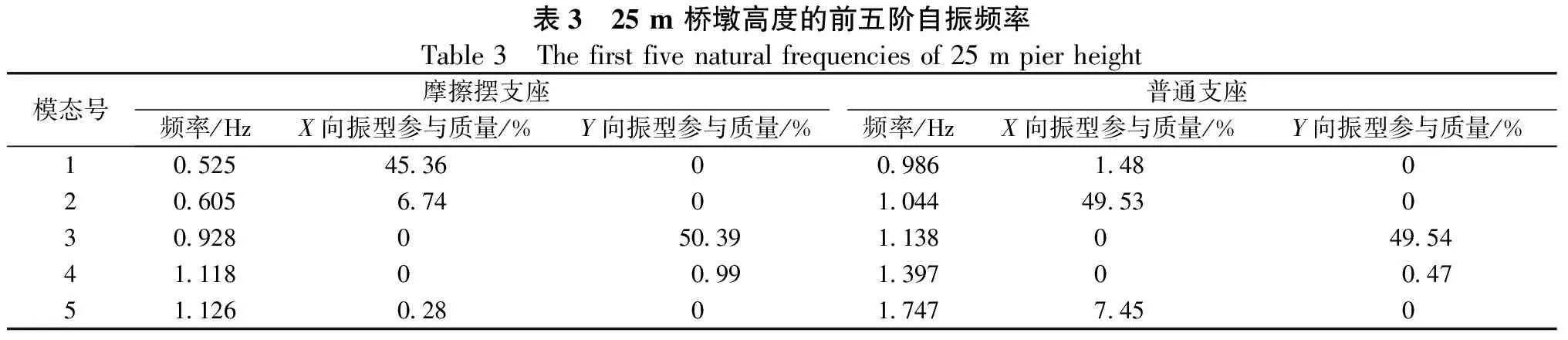
表3 25 m 桥墩高度的前五阶自振频率Table 3 The first five natural frequencies of 25 m pier height模态号摩擦摆支座普通支座频率/HzX向振型参与质量/%Y向振型参与质量/%频率/HzX向振型参与质量/%Y向振型参与质量/%10.52545.3600.9861.48020.6056.7401.04449.53030.928050.391.138049.5441.11800.991.39700.4751.1260.2801.7477.450

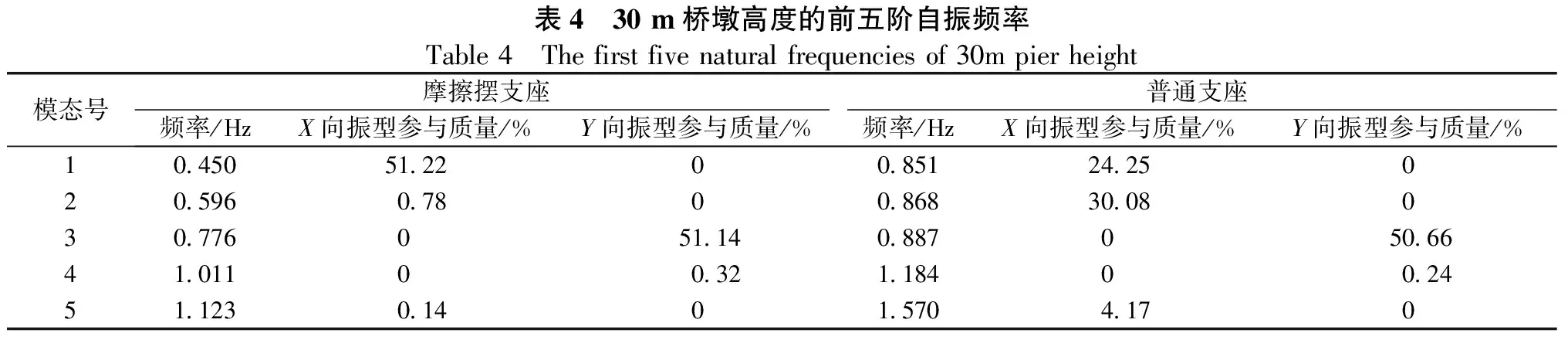
表4 30 m桥墩高度的前五阶自振频率Table 4 The first five natural frequencies of 30m pier height模态号摩擦摆支座普通支座频率/HzX向振型参与质量/%Y向振型参与质量/%频率/HzX向振型参与质量/%Y向振型参与质量/%10.45051.2200.85124.25020.5960.7800.86830.08030.776051.140.887050.6641.01100.321.18400.2451.1230.1401.5704.170

从表1～表4中可以得出，随着桥墩高度的增加，隔震桥梁与非隔震桥梁的自振频率随之减小。当8#桥墩高度从15 m增大至30 m时，隔震桥梁的五阶模态自振频率从1.467下降到1.123，非隔震桥梁的三阶模态自振频率从1.887减小至1.570。当桥墩高度大于25 m 时，非隔震桥梁自振频率减小的速率更快。

4.2 顺桥向内力与位移

当地震波输入，可以得到顺桥向和横桥向的内力和位移动力响应幅值。图6～图9分别列出地震波作用下，桥墩高度的变化对隔震和非隔震桥梁顺桥向墩底剪力、弯矩和墩顶位移的影响。

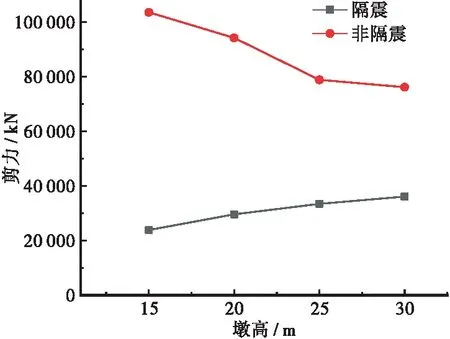
图6 顺桥向墩底剪力与墩高的关系

图7 顺桥向墩底弯矩与墩高的关系

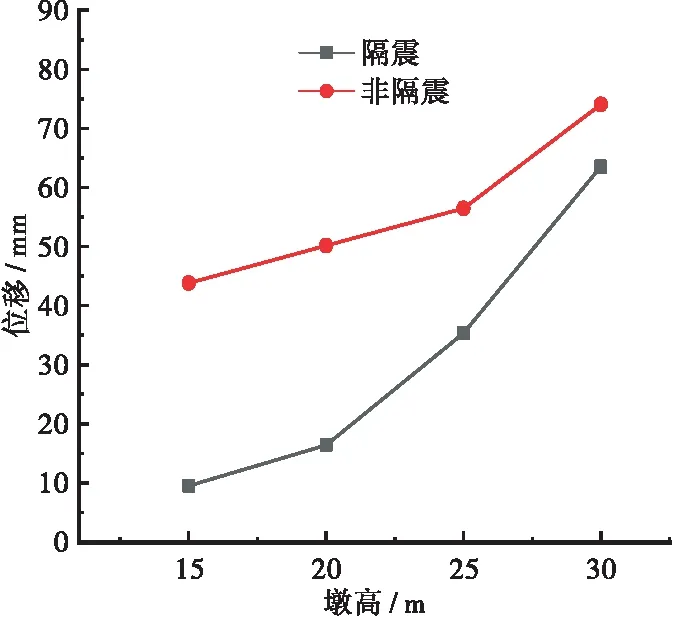
图8 顺桥向墩顶位移与墩高的关系

图9 顺桥向支座处梁体位移与墩高的关系

非隔震桥梁的顺桥向剪力和弯矩都随着桥墩高度的增加而逐渐减小，当桥墩高度15 m时，剪力为1.04×105kN，弯矩为1.15×106kN·m；当桥墩高度30 m时，剪力为7.62×104kN，弯矩为9.83×105kN·m，剪力减小了26.7%，弯矩减小了14.5%。而隔震桥梁的顺桥向剪力和弯矩随着桥墩高度的增加逐渐增大，当桥墩高度15 m时，剪力为2.38×104kN，弯矩为2.08×105kN·m；当桥墩高度30 m时，剪力为3.61×104kN，弯矩为7.02×105kN·m，剪力增大了51.7%，弯矩增大了237.5%。墩底的弯矩受剪力影响较大，隔震桥梁的墩底剪力变大幅度不明显，但弯矩增大很明显，这是因为受桥墩高度增加所导致，桥墩越高，墩底弯矩增大越明显。在非隔震桥梁中，其剪力和弯矩都同时减小，但变化幅值不大。这说明桥墩高度的增加对隔震桥梁抗震性能的减弱更为明显。

隔震桥梁与非隔震桥梁的墩顶位移都随着墩高的增大而增大。墩高15 m时，非隔震和隔震桥梁顺桥向墩顶位移分别为43.8、9.5 mm。墩高30 m时，非隔震和隔震桥梁横桥向墩顶位移分别为74.1、63.5 mm。顺桥向支座处梁体位移随墩高的增加位移也逐渐增加，相比于非隔震桥梁，隔震桥梁的位移较大，在隔震桥梁中支座处桥墩与梁体相对位移最大值为223.6 mm，没有超过摩擦摆支座的限值位移。因为随着墩高的增加，桥墩柔度变大，地震作用下墩顶位移也增大。在隔震桥梁中，桥墩高度在增大的过程中，已成为一个影响桥梁抗震的关键因素。桥墩依靠自身柔度的增大使地震传输至上部结构的能量减小，摩擦摆支座不能充分发挥作用。

4.3 横桥向内力与位移

图10～图13分别列出地震波作用下，桥墩高度变化对横桥向的墩底剪力、弯矩和墩顶位移的影响。

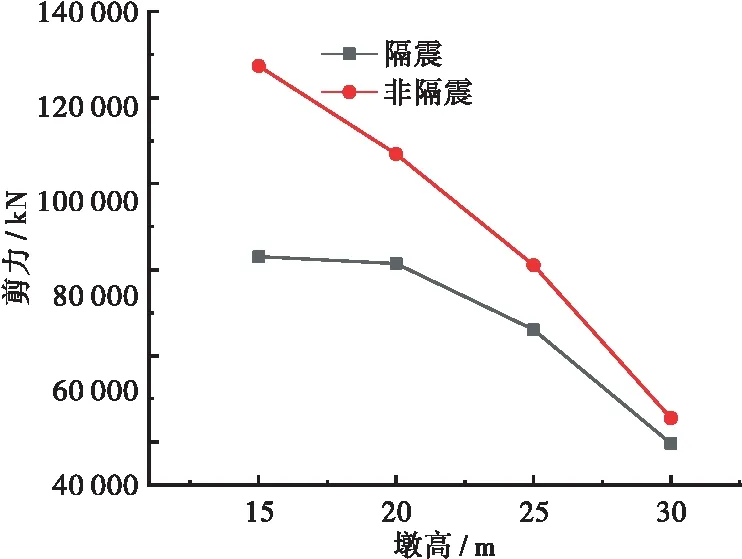
图10 横桥向墩底剪力与墩高的关系

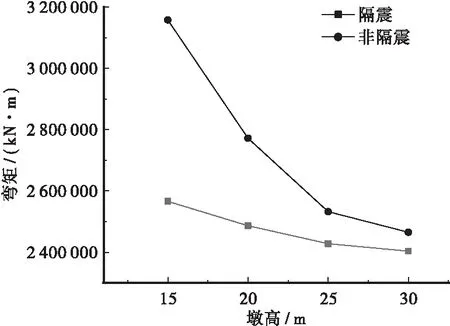
图11 横桥向墩底弯矩与墩高的关系

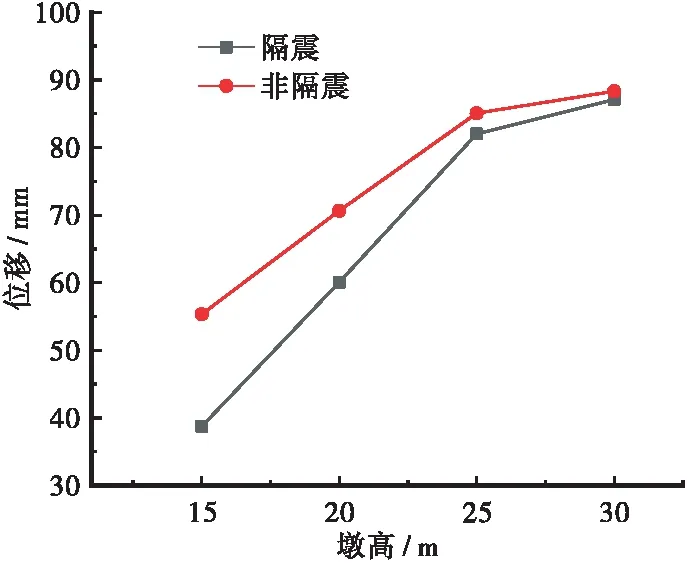
图12 横桥向墩顶位移与墩高的关系

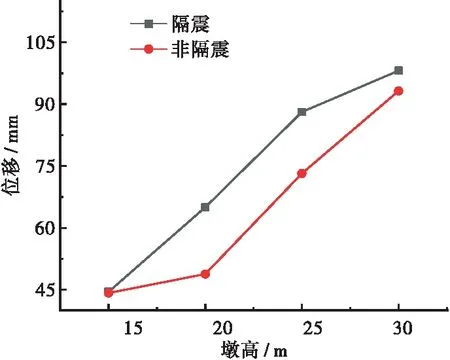
图13 横桥向支座处梁体位移与墩高的关系

在非隔震桥梁中，随着墩高的增加，墩底剪力和弯矩都逐渐减小。墩高15 m时，剪力为1.274×105kN，弯矩为3.158×106kN·m；墩高为30 m时，剪力为4.55×104kN，弯矩为2.465×106kN·m。其中剪力减小了64.29%，弯矩减小了21.94%，剪力减小的幅度较大，弯矩减小的幅度较小。在隔震桥梁中，随墩高增加，剪力和弯矩都逐渐减小。墩高15 m时，剪力为8.307×104kN，弯矩为2.566×106kN·m；墩高为30 m时，剪力为3.957×104kN，弯矩为2.404×106kN·m。其中剪力减小了52.37%，弯矩减小了6.31%，剪力减小幅度较大，弯矩减小幅度较小。与顺桥向墩底内力相比，横桥向内力值大于顺桥向。

隔震桥梁与非隔震桥梁的墩顶位移随着墩高的增大而增大。墩高15 m时，非隔震和隔震桥梁横桥向墩顶位移分别为55.3、38.7 mm。墩高30 m时，非隔震和隔震桥梁横桥向墩顶位移分别为88.3、87.1 mm。横桥向支座处梁体位移随着墩高的增加位移也逐渐增加，在隔震桥梁中支座处桥墩与梁体相对位移最大值为198.3 mm，没有超过摩擦摆支座的限值位移。与顺桥向墩顶位移相比，横桥向的位移值都大于顺桥向。

4.4 隔震率

为了方便比较不同工况下的隔震效果，以隔震率作为评价标准，选择墩底剪力、弯矩和墩顶位移3项指标进行计算。隔震率计算公式如下：

其中，λ表示隔震率，X0和X分别表示非隔震桥梁和隔震桥梁的地震响应幅值。

图14、图15分别展示了顺桥向和横桥向的剪力、弯矩、位移和隔震率的变化关系。

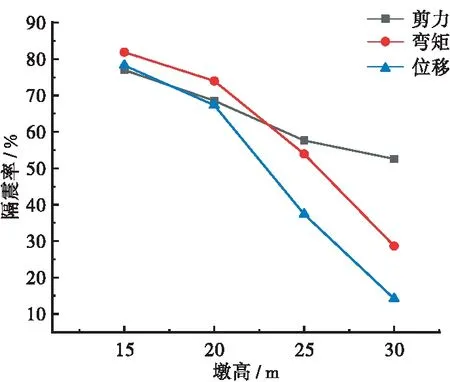
图14 顺桥向隔震率与墩高的关系

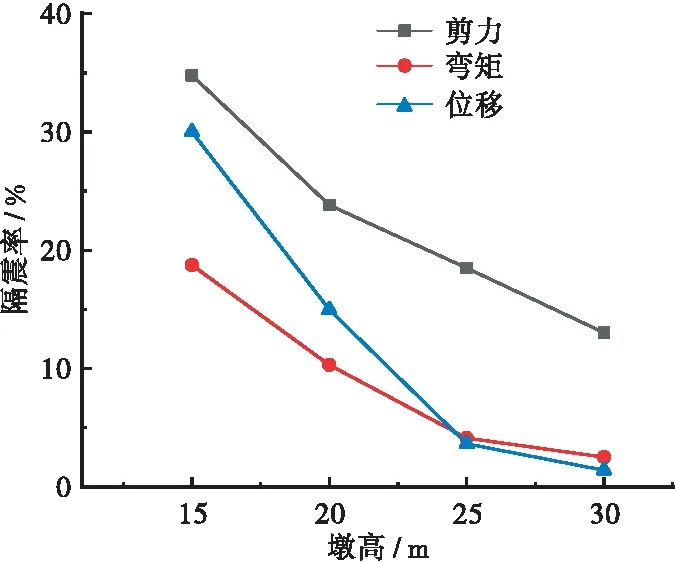
图15 横桥向隔震率与墩高的关系

当墩高从15 m增加到30 m时，顺桥向墩底剪力的隔震率从73.99%下降到52.58%，墩底弯矩的隔震率从81.89%下降到28.63%，墩顶位移的隔震率从78.25%下降到14.20%。横桥向墩底剪力的隔震率从34.79%下降到13.02%，墩底弯矩的隔震率从18.74%下降到2.50%，墩顶位移的隔震率从30.01%下降到1.39%。

由图14、图15可以看出，顺桥向隔震率大于横桥向；顺桥向隔震率下降幅度大于横桥向。随着墩高的增加，顺桥向和横桥向内力与位移的隔震率逐渐下降。这说明随着墩高的增加，摩擦摆支座逐渐丧失了隔震效果。