钢-混凝土组合箱梁刚构桥弹塑性地震反应分析

刘 军，陈双庆，付 磊

(1.湖南路桥建设集团有限责任公司，湖南 长沙 410075； 2.中南大学 土木工程学院，湖南 长沙 410075；3.湖南文理学院，湖南 常德 415000)

连续刚构桥因桥下净空大、桥跨大、能节省桥墩支座的优点，被大量应用在实际桥梁工程中[1-5]，如图1(a)、图1(b)所示。以往传统的连续刚构桥，桥墩一般采用矩形、圆形或圆端形钢筋混凝土桥墩，主梁一般采用钢筋混凝土箱梁，结构自重较大，延性和抗震性能相对较差，如图1(c)所示。对于需要穿过深阔的峡谷，地况复杂山区的桥梁结构，桥墩同时受到轴力和弯矩的共同作用，既要满足极限承载力的要求，又要满足桥墩在高速动荷载下动力性能的要求，还要满足抗震的要求，因此要求桥墩柱要有足够刚度和较好的延性和优良的抗震性能[6-7]。

近年来，连续刚构桥的抗震研究主要集中在对钢筋混凝土桥墩-钢筋混凝土预应力梁连续刚构桥进行反应谱动力时程分析的线弹性计算、静力弹塑性计算、基于杆件的纤维模型分析计算，且多数研究都基于实际工程为背景，如樊健生等[8]基于Opensees软件对钢筋混凝土桥墩与钢-混凝土组合箱梁的组合刚构桥进行了静力弹塑性研究，分析了地震波不同输入方向和地震波随机性对桥梁地震响应的影响，并对桥梁最大位移响应进行评价和预测；周淑芬等[9]利用有限元软件Midas Civil和XTRACT程序比较了钢管混凝土桥墩和钢筋混凝土桥墩非线性动态时程分析的动力特性与耗能性能，结果表明：钢管混凝土桥墩可以很好地降低结构地震响应，对结构抗震较为有利，可以作为高地震烈度区域桥梁墩柱的理想形式，如图1(d)所示。为此，综合考虑经济因素和满足刚度、承载力与抗震性能等要求，可采用圆端形钢管混凝土桥墩代替钢筋混凝土桥墩，因为相同截面尺寸下，钢管混凝土柱比钢筋混凝土柱的承载力和刚度高、延性好、抗震性能强，且很方便地通过焊接将组合梁底部与钢管混凝土顶部固结。文华斌等[10]采用ANSYS有限元软件进行了圆钢管混凝土格构柱桥墩-钢筋混凝土箱梁桥的动力特性、反应谱和动力时程分析，考虑了地震波输入方向和行波效应的影响，探讨了墩顶位移、墩底轴力、剪力和弯矩等内力在地震作用下的特征，为工程的抗震设计提供了借鉴；胡靖等[11]基于试验和采用MIDAS建立的钢管混凝土格构柱高墩大跨连续刚构桥有限元模型，分析了其动力特性分析和地震响应，评估了其抗震性能。综上所述，地震作用下传统的反应普法仅关注承载力是否满足抗震要求，基于杆件截面层次的纤维模型分析方法难以合理反映桥墩、组合箱梁中各材料之间的相互作用特性，也无法分析组合桥梁的地震耗能与其耗能机制。

(a)传统的连续刚构桥(日本下浜鮎川)

随着组合刚构桥在我国桥梁中应用日益增多，为保证生命交通线的安全，需要进行更加精细地计算和研究其抗震性能。为此，本文开展工作如下：①在既有研究的基础上，采用ABAQUS有限元软件建立圆端形钢管混凝土桥墩-钢混凝土组合箱梁刚构桥三维实体有限元模型；②开展4种地震工况下组合刚构桥地震弹塑性时程分析，探讨各关键部位的绝对位移、绝对加速度、墩底剪力与钢管、钢箱梁、钢筋、栓钉、混凝土的应力应变等变化规律，揭示桥墩钢管与混凝土相互作用关系；③比较箱梁双重组合作用、不同墩高和截面尺寸、地震作用方向等工况下组合刚构桥耗能分配机理，为工程设计提供参考。

1 研究背景与设计条件

本文在文献[12]中的组合刚构桥既有研究基础上，以圆端形钢管混凝土桥墩-组合箱梁刚构桥为研究对象，组合刚构桥由桥面主梁、墩柱和两者之间的固结节点3部分组成，桥梁整体跨度和各构件截面形状尺寸如图2所示，跨度为50 m+75 m+50 m三跨组合刚构桥，桥墩柱采用圆端形钢管混凝土墩柱，高度为40 m+60 m+60 m+40 m，截面尺寸为2.5 m×1.5 m，截面含钢率为4%；桥面板采用变截面钢-混凝土组合箱梁的形式，其中箱形组合梁在桥墩支座两端各15 m的负弯矩区域的箱梁底部钢板内浇筑300 mm厚的混凝土和布置栓钉，既可以发挥混凝土抗压作用，又可以提高钢箱梁底板和腹板的稳定性，从而使连续组合梁桥在中支座附近形成双重的组合作用并减小钢板厚度。

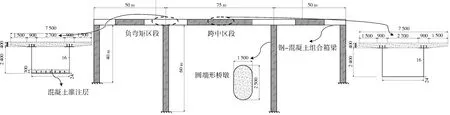
图2 三跨组合刚构桥整体尺寸和截面示意图(单位：mm)

其中组合箱梁的总高度为2.8 m、宽度为7.5 m，箱梁上翼缘为变截面的混凝土桥面板，同时布置3排栓钉，并在负弯矩区域布置混凝土面板和7排栓钉，混凝土板的厚度为400 mm，纵向和横向分别配φ22@200和φ16@200的受力钢筋，腹板采用16 mm厚钢板，高度为2 400 mm，箱梁底部钢板厚度为24 mm，宽度为3 500 mm，并在箱梁内部设置横向隔板以提高箱梁的整体稳定性。

结构中混凝土采用C40，钢材采用Q235，栓钉和钢筋均采用HRB335，各材料属性见表1。考虑桥梁结构的自重，取重力加速度为9.8 m/s2，根据《公路桥涵设计通用规范》(CJJ D60—2015)[13]中公路-I级荷载的相关规定、《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTGD62—2015)[14]中相关规定，本文所设计的主梁各部位的抗力和最大挠度均满足规范设计要求。

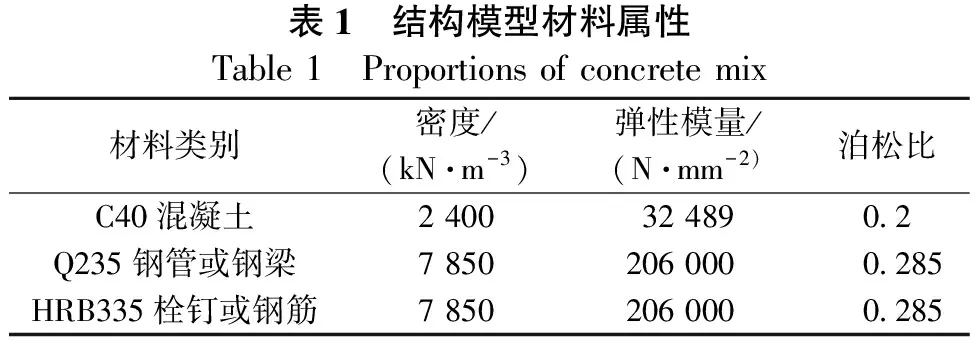
表1 结构模型材料属性Table 1 Proportions of concrete mix材料类别密度/(kN·m-3)弹性模量/(N·mm-2)泊松比C40混凝土2 40032 4890.2Q235钢管或钢梁7 850206 0000.285HRB335栓钉或钢筋7 850206 0000.285

2 组合刚构桥有限元模型

2.1 有限元模型建立

考虑模型中钢管与核心混凝土的套箍约束作用与地震荷载的损伤累计效应，本文采用ABAQUS有限元软件，材料本构关系参考文献[15]。在既有研究的基础上，钢-混凝土组合箱梁和框架的抗震性能在文献[16]中做了有限元分析验证，均取得了良好的计算结果；参照相同的建模分析方法，采用实体单元(C3D8R)模拟混凝土柱、板，采用壳单元(S4R)模拟钢管、钢梁，桥面板中的钢筋和栓钉分别采用桁架单元(T3D2)和梁单元(B31)，建立三跨圆端形钢管混凝土桥墩-钢混凝土组合箱梁刚构桥非线性三维实体有限元模型。

对全桥模型进行抗震分析时，桥墩底部的边界条件采用全固结的方式，即在圆端形桥墩柱底部对U1、U2、U3、UR1、UR2、UR3这6个方向的自由度进行限制约束，而对桥墩柱与箱梁采用绑定(Tie)的约束方式，即桥墩柱与箱梁全固结；将组合梁受力筋与箍筋进行合并(merge)，再与桥面板采用内置(embedded region)约束形式；对于钢管与混凝土柱的界面，采用库伦摩擦型接触，由切线方向的黏结滑移和法线方向的硬接触构成，摩擦系数取0.5，并采用有限滑移(finited sliding)以满足计算效率。在进行刚构桥地震加载时，采用不同峰值加速度下地震波来分析组合刚构桥三维实体有限元模型在各种设防烈度等级下的弹塑性动力性能时程反应。有限元模型如图3所示。

图3 三跨刚构桥有限元模型

2.2 模态分析

圆端形钢管混凝土桥墩-钢混凝土组合箱梁刚构桥模态分析的前4阶阵型的特征值、圆频率、固有频率和广义质量见表2。本文中主要给出了前4阶模态分析的结果，前4阶典型的阵型基本均表现出整体振动的特性，第一阶阵型和第二阶阵型均为地震波输入向X轴方向的平动，第三阶阵型和第四阶阵型表现为X轴向平动和Z轴向的整体单波形扭转振动。前4阶阵型图如图4所示。

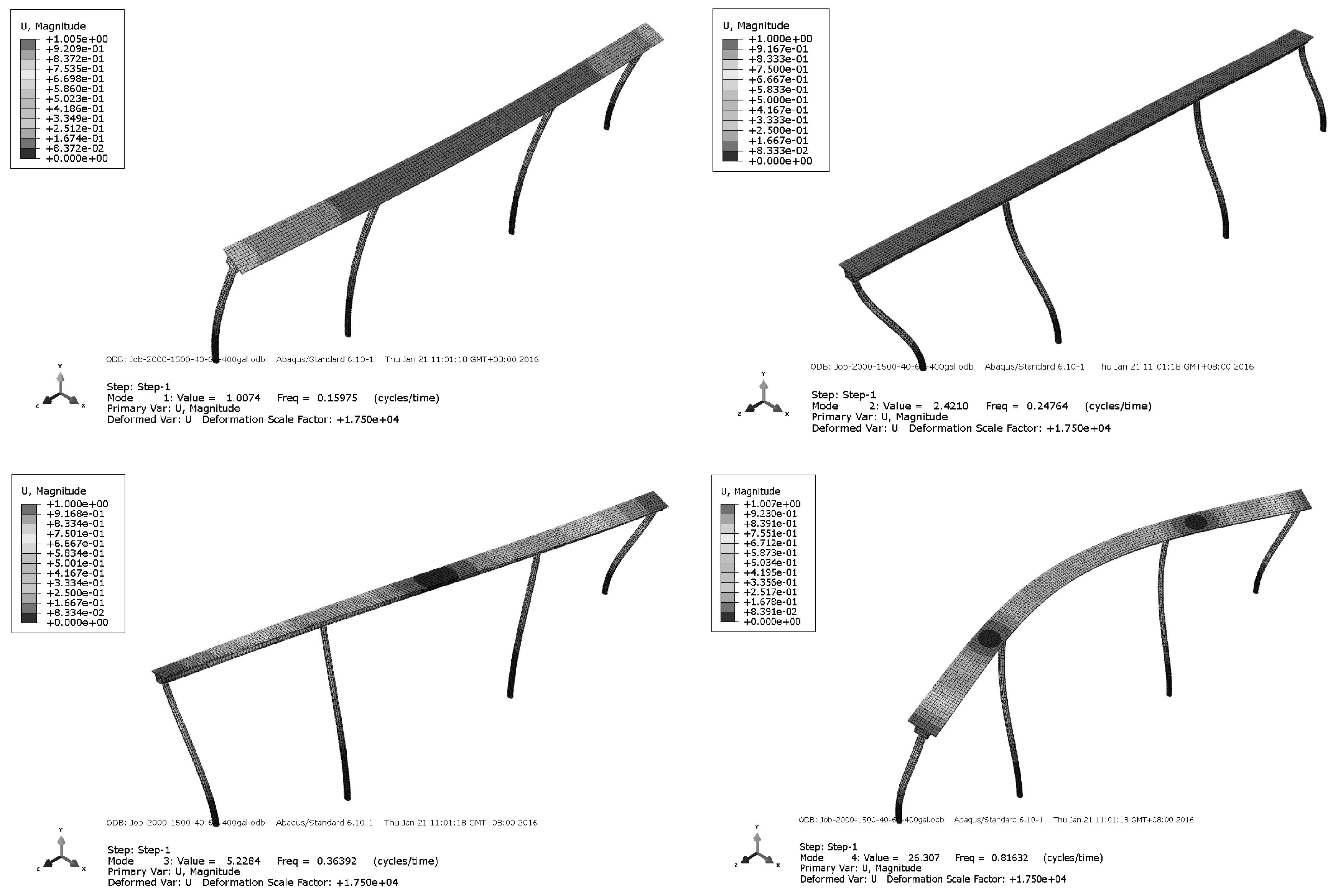
图4 刚构桥前4阶阵型

表2 结构模型的自振频率Table 2 Natural vibration frequency of structural model阵型编号特征值圆频率ω固有频率f广义质量11.81.30.21 867.123.11.70.32 443.237.82.70.41 003.3430.75.50.9688.1

2.3 阻尼参数设置

ABAQUS有限元软件在对结构动力弹塑性分析中通常使用Rayleigth阻尼[15]：

[C]=α[M]+β[K]

(1)

其中，[C]为阻尼矩阵；[M]为质量矩阵；[K]为刚度矩阵。通过模态分析，可计算出结构的圆频率(ωi，ωj)，取值见表2；α和β分别为与质量成比例和与刚度成比例的Rayleigth阻尼系数，按照下式计算，取阻尼比ξi=ξj=0.03，可得α=0.04、β=0.02。

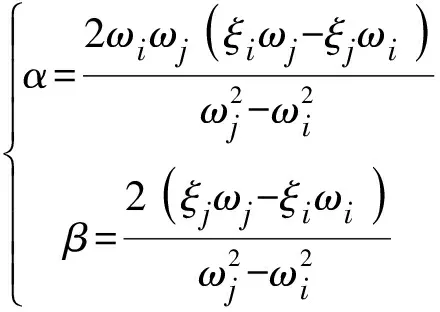
(2)

3 全桥结构弹塑性时程分析原理

对本文中的刚构桥进行地震加载时，采用不同峰值加速度下地震波来分析在各种设防烈度等级下的地震作用的弹塑性动力性能时程反应，按照《公路桥梁抗震设计规范》(JTG/T 2231-01—2020)[17]中的相关规定，可对地震动进行比例调幅，将实际地震记录的峰值加速度[a(t)max]折算成所需的基本烈度即可使用。本章选取地震波类型为EL-Centro波(N-S)，见表3，地震波持续时间为20 s，调整之后的峰值加速度分别为100、200、300和400 Gal，见图5。

表3 所选用地震波Table 3 Seismic waves are selected地震波名称方向日期加速度峰值/Gal时间间隔/sEL-Centro波N-S1940-5-18341.70.02

图5 EI-Centro波N-S向在各种地震烈度下的地震动加速度

全桥结构在横桥向(X向)地震波输入下的振动方程为[29]：

(3)

4 组合刚构桥地震分析结果

4.1 横桥向地震作用下绝对位移和加速度时程响应分析

4种地震烈度下各关键部位处的水平位移和加速度时程曲线对比分别见图6和图7，最大绝对位移、加速度值和发生时间见表4。可知：①4种地震烈度下正、负向的绝对最大位移和加速度表现出一致的规律，即接近跨中部位的位移较边跨的大，为最不利部位；桥面板的绝对加速度要大于边跨和中跨桥墩；②边跨桥墩的正向绝对最大位移发生的时刻较为接近，基本在11.2～14.2 s范围内；地震强度越大，负向最大绝对位移发生时刻要早，分别为13.3、12.7、4.5、4.4 s；中跨桥墩和桥面板中心点的正、负向最大绝对位移发生时刻均比较接近。

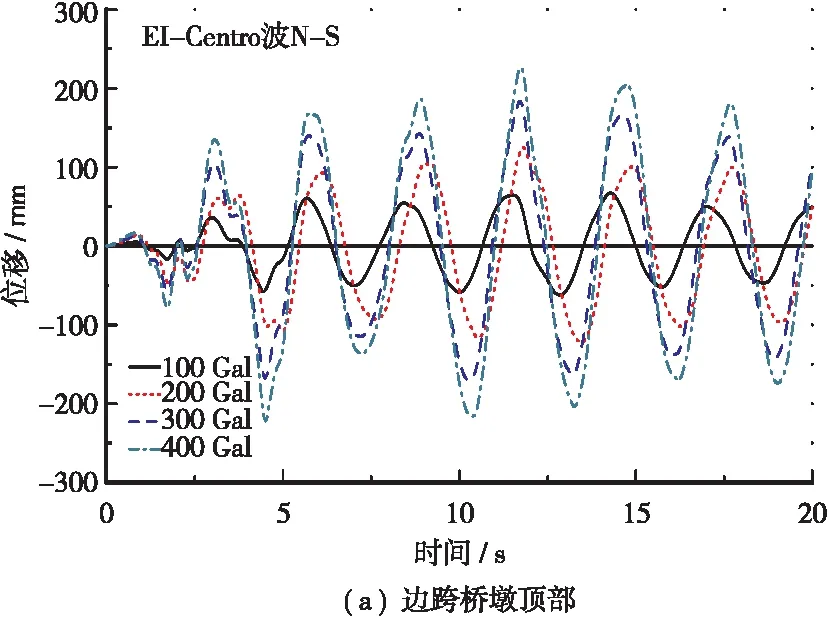
图6 刚构桥各关键部位处的绝对位移时程曲线

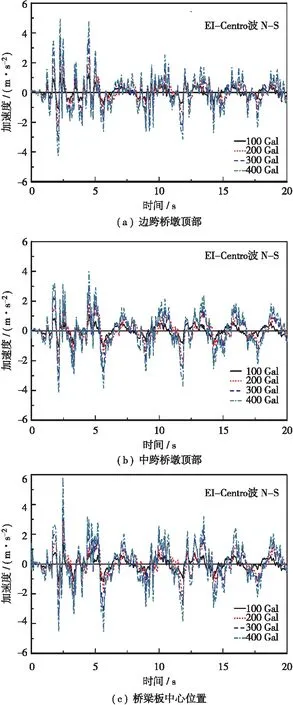
图7 刚构桥各关键部位处的绝对加速度时程曲线

4.2 横桥向地震作用下柱底剪力时程反应

四种地震烈度下边跨和中跨墩底的剪力时程曲线对比见图8，剪力和其墩顶绝对位移的关系曲线见图9，最大剪力值和对应时刻见表5。可知：①边跨墩底的峰值剪力均大于中跨墩底的峰值剪力，且边跨墩底的峰值剪力发生的时刻均滞后于中跨墩底，地震烈度越大，对中跨墩底峰值剪力发生时刻的影响要大于边跨墩底；②随着地震烈度的增大，对于边跨墩底的峰值剪力，后者相对前者分别增大1.7、1.4和1.2倍，而对于中跨墩底的峰值剪力，分别增大2.1、1.3和1.3倍；③边跨、中跨墩底的总剪力和其墩顶绝对位移的滞回环主要呈现在二四象限内，都相对较为扁平，但在400 Gal地震波作用下，其滞回环相对前3种都饱满。

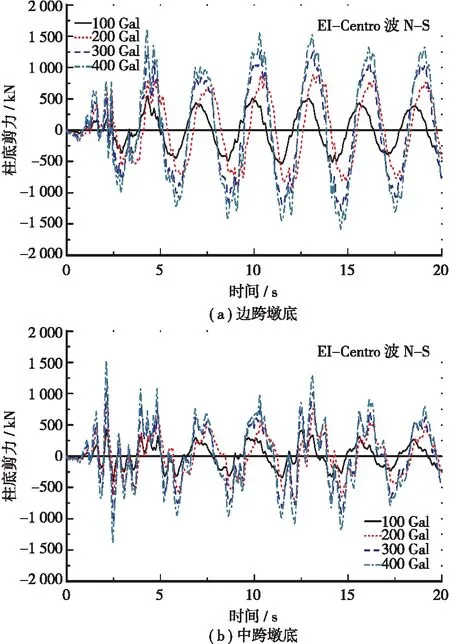
图8 刚构桥墩底剪力时程曲线

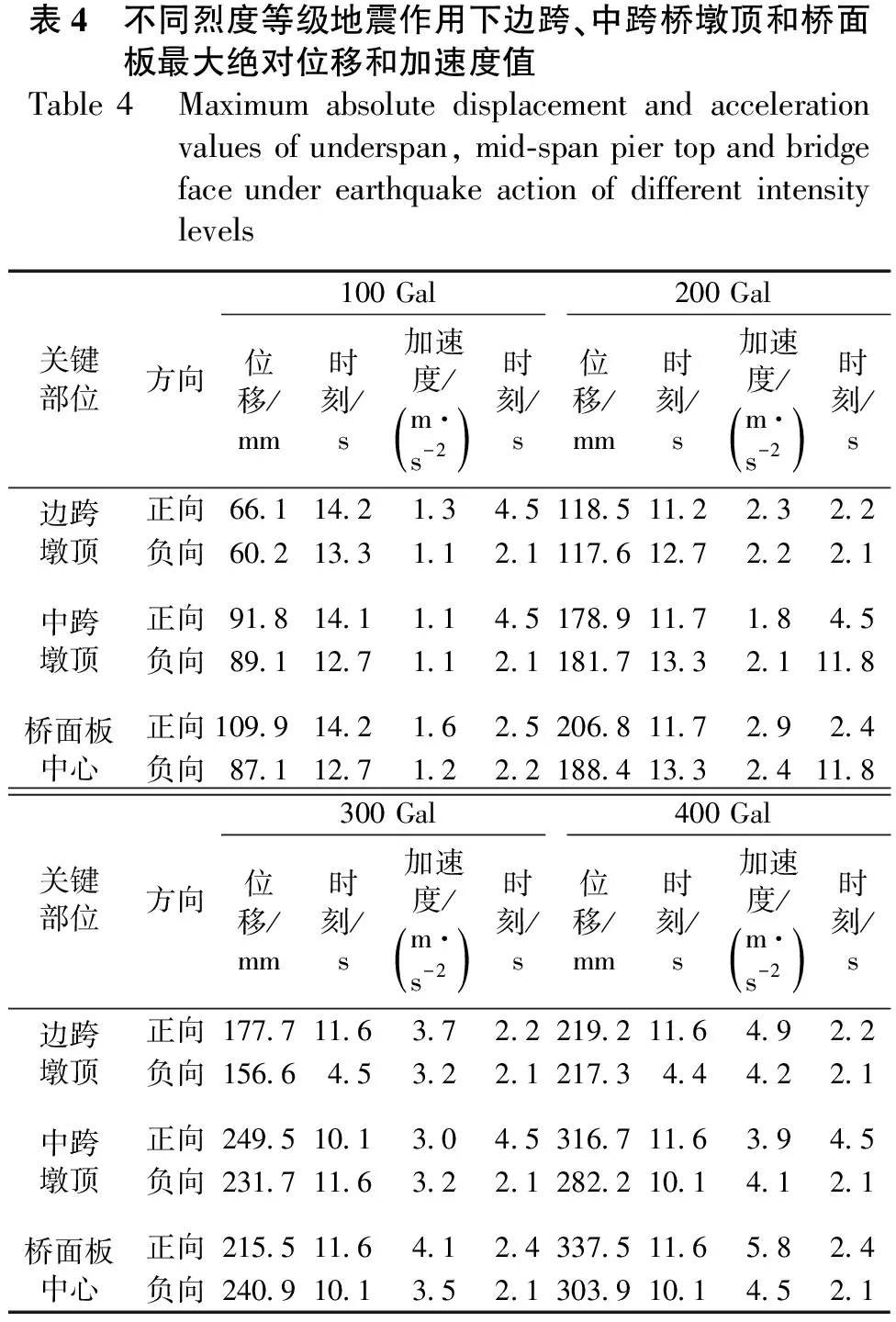
表4 不同烈度等级地震作用下边跨、中跨桥墩顶和桥面板最大绝对位移和加速度值Table 4 Maximum absolute displacement and acceleration values of underspan, mid-span pier top and bridge face under earthquake action of different intensity levels关键部位方向100 Gal200 Gal位移/mm时刻/s加速度/m·s-2()时刻/s位移/mm时刻/s加速度/m·s-2()时刻/s边跨墩顶正向66.114.21.34.5118.511.22.32.2负向60.213.31.12.1117.612.72.22.1中跨墩顶正向91.814.11.14.5178.911.71.84.5负向89.112.71.12.1181.713.32.111.8桥面板中心正向109.914.21.62.5206.811.72.92.4负向87.112.71.22.2188.413.32.411.8关键部位方向300 Gal400 Gal位移/mm时刻/s加速度/m·s-2()时刻/s位移/mm时刻/s加速度/m·s-2()时刻/s边跨墩顶正向177.711.63.72.2219.211.64.92.2负向156.64.53.22.1217.34.44.22.1中跨墩顶正向249.510.13.04.5316.711.63.94.5负向231.711.63.22.1282.210.14.12.1桥面板中心正向215.511.64.12.4337.511.65.82.4负向240.910.13.52.1303.910.14.52.1

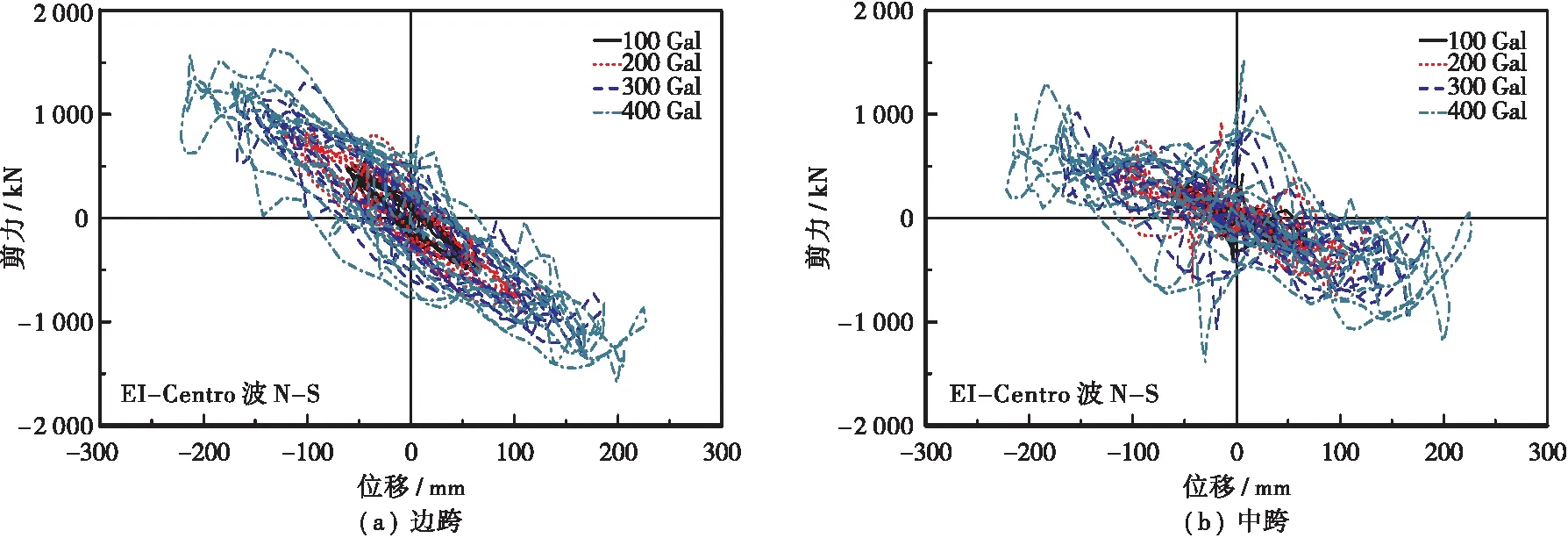
图9 刚构桥各关键点处的柱底剪力时程曲线

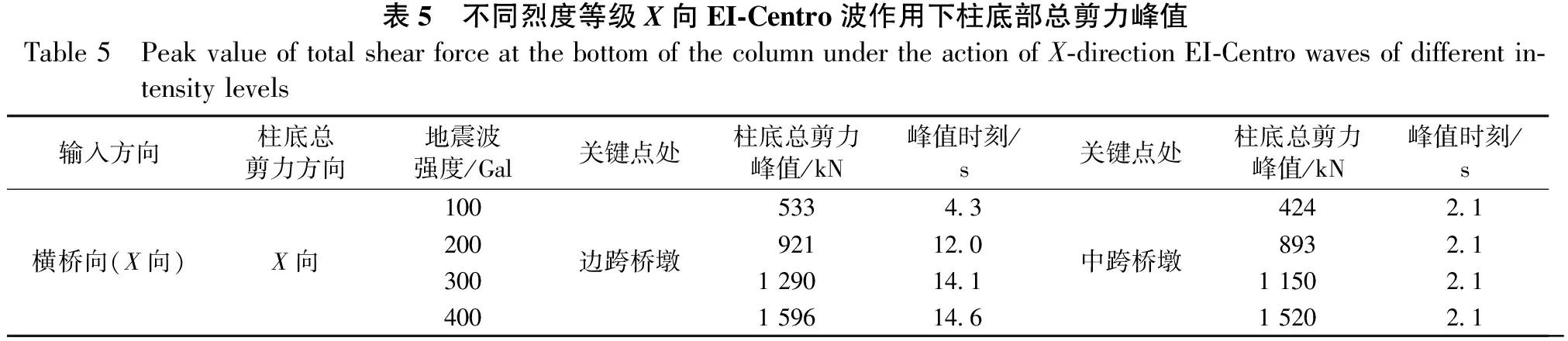
表5 不同烈度等级X向EI-Centro波作用下柱底部总剪力峰值Table 5 Peak value of total shear force at the bottom of the column under the action of X-direction EI-Centro waves of different in-tensity levels输入方向柱底总剪力方向地震波强度/Gal关键点处柱底总剪力峰值/kN峰值时刻/s关键点处柱底总剪力峰值/kN峰值时刻/s1005334.34242.1横桥向(X向)X向200边跨桥墩92112.0中跨桥墩8932.13001 29014.11 1502.14001 59614.61 5202.1

4.3 横桥向地震作用下应力-应变响应分析

该三跨连续刚构桥呈对称结构，为此只对其中一个边跨桥墩柱、箱梁和一个中跨桥墩柱、箱梁的关键部位进行应力应变时程分析，根据400 Gal地震波作用下桥梁模型应力云图，找到最不利控制点。可知：①如图10和表6所示，边跨桥墩的钢管最大应力值要大于中跨桥墩，且在地震后期，边跨墩顶处钢管的应力表现出非线性的增大，并达到钢材的屈服强度(235 MPa)，钢管进入了塑性阶段；②边跨桥墩顶、墩底和中跨墩底的混凝土应力均达到轴心抗压强度(39.3 MPa)，表明在钢管对混凝土产生套箍约束作用，各关键部位处混凝土的应力-应变曲线均表现了良好的滞回性能，也能产生较多的耗能；③如图11和表7、表8所示，中跨支座负弯矩处钢箱梁翼缘板、中跨跨中钢箱梁底板与相应处栓钉的应力值均已屈服，说明该部位在地震作用下受力较大；④如图12和表9所示，在地震前期，上部桥面板钢筋处于弹性工作阶段，后期中跨墩顶负弯矩处、中跨跨中处的桥面钢筋与箱梁底部中跨支座负弯矩处钢筋逐渐屈服(大于335 MPa)，说明箱梁的双重组合作用对桥梁结构的抗震是有利的。

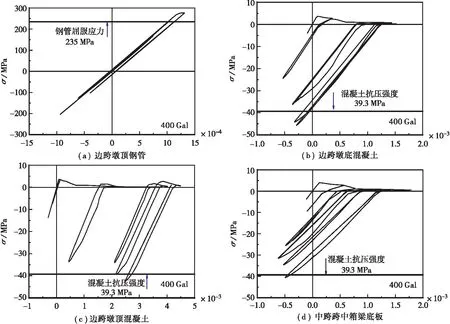
图10 钢管混凝土墩柱控制点处的应力-应变曲线

表6 钢管混凝土墩柱各控制点处最大应力值(σmax)和出现时刻(t)Table 6 Maximum stress value (σmax) and occurrence time (t) at each control point of concrete-filled steel tube pier column钢管各控制点σmax/MPat/s混凝土各控制点σmax/MPat/s边跨墩底197.910.3边跨墩底44.214.6边跨墩顶269.011.6边跨墩顶40.513.3中跨墩底182.013.1中跨墩底40.614.7中跨墩顶42.614.4中跨墩顶22.8 13.4

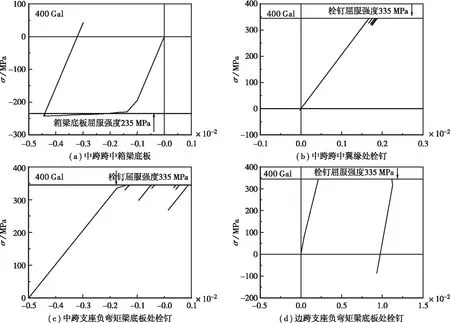
图11 钢箱梁各控制点处的应力时程曲线

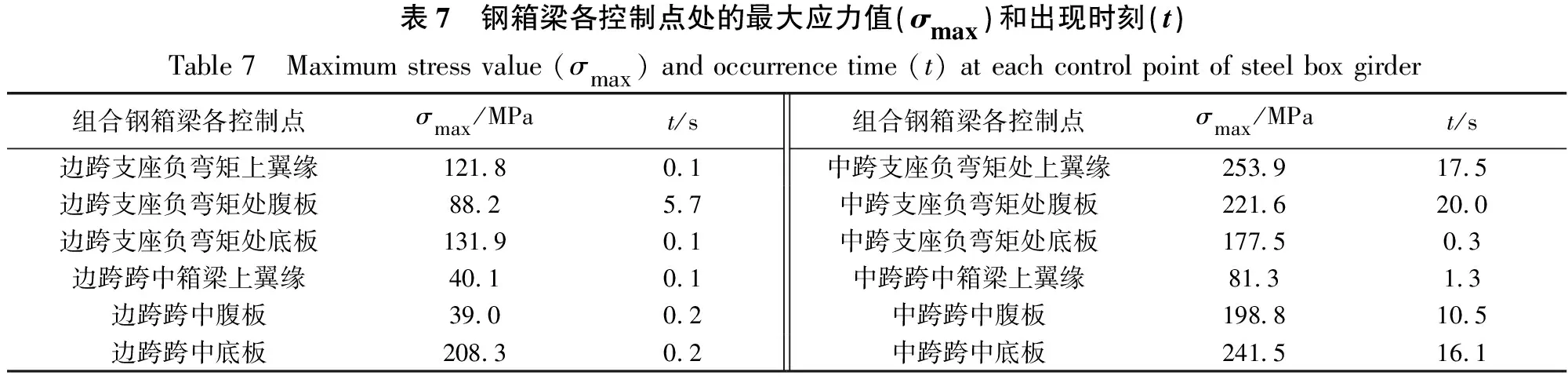
表7 钢箱梁各控制点处的最大应力值(σmax)和出现时刻(t)Table 7 Maximum stress value (σmax) and occurrence time (t) at each control point of steel box girder组合钢箱梁各控制点σmax/MPat/s组合钢箱梁各控制点σmax/MPat/s边跨支座负弯矩上翼缘121.80.1中跨支座负弯矩处上翼缘253.917.5边跨支座负弯矩处腹板88.25.7中跨支座负弯矩处腹板221.620.0边跨支座负弯矩处底板131.90.1中跨支座负弯矩处底板177.50.3边跨跨中箱梁上翼缘40.10.1中跨跨中箱梁上翼缘81.31.3边跨跨中腹板39.00.2中跨跨中腹板198.810.5边跨跨中底板208.30.2中跨跨中底板241.516.1

表8 栓钉各控制点处的最大应力值(σmax)和出现时刻(t)Table 8 Maximum stress value (σmax) and occurrence time (t) at each control point of bolt栓钉各控制点σmax/MPat/s栓钉各控制点σmax/MPat/s边跨支座负弯矩翼缘板处259.00.2边跨支座负弯矩梁底板处305.00.1边跨跨中翼缘板处264.30.2中跨支座负弯矩梁底板处335.00.4中跨支座负弯矩翼缘板处335.00.5距中跨墩顶中心线位置最远梁底板处310.00.3中跨跨中翼缘板处335.05.5

图12 上部和底部钢筋混凝土板各控制点处的应力-应变关系曲线

表9 上部和底部钢筋混凝土板各控制点处的最大应力值(σmax)和出现时刻(t)Table 9 Maximum stress value (σmax) and occurrence time (t) at each control point of the upper and bottom RC slabs箱梁上部钢筋和混凝土各控制点σmax/MPat/s箱梁底部钢筋和混凝土各控制点σmax/MPat/s中跨墩顶负弯矩处钢筋368.020.0边跨墩顶负弯矩处钢筋238.95.4中跨跨中处钢筋357.614.4中跨墩顶负弯矩处钢筋371.314.7中跨墩顶负弯矩处混凝土板2.40.1边跨墩顶负弯矩处混凝土板7.210.1中跨跨中处混凝土板23.22.5中跨墩顶负弯矩处混凝土板29.13.1

4.4 横桥向地震作用下桥墩柱横向变形系数分析

图13给出了4种地震波作用下边跨、中跨墩底控制点处的横向变形系数时程曲线，可知：①随着地震波强度的增大，边跨、中跨墩底的横向变形系数的峰值分别为0.64、0.92、0.97、0.98和0.66、0.91、0.96、0.97，说明钢管的环向应变就越大，即环向应变与纵向应变的比值就越大(均大于0.5)，钢管对核心混凝土的套箍约束作用也越大；②地震初期，边跨桥墩的横向变形系数最大值达0.75，而中跨桥墩柱其值在0～0.5，随后两者相差较小，说明在地震作用前期，边跨桥墩地震响应更大，钢管表现出较强的约束性能。

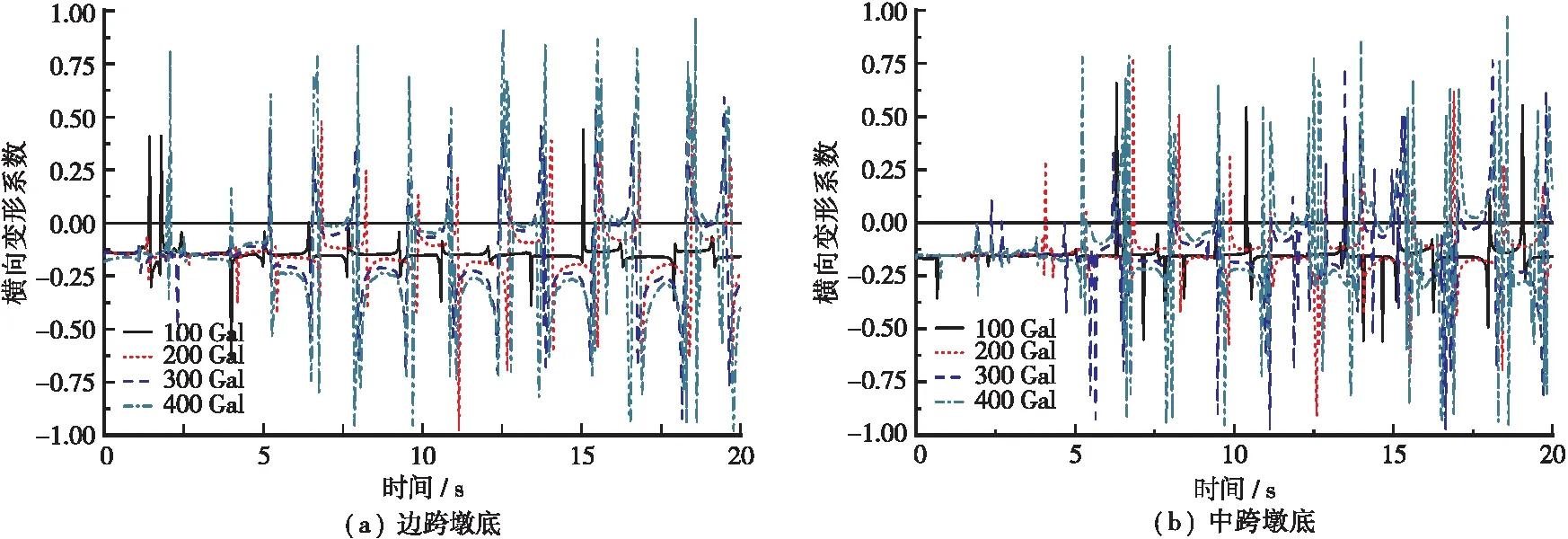
图13 刚构桥桥墩横向变形系数时程曲线

4.5 地震作用下刚构桥塑性耗能分析

图14给出了400 Gal地震作用下刚构桥各构件塑性耗能占比情况，据此可知：①图14(a)所示为组合箱梁塑性耗能分配，钢箱梁的耗能最大，其次为钢筋混凝土桥面板，栓钉耗能最小；②边跨和中跨桥墩、桥墩钢管和混凝土的塑性耗能见图14(b)和图14(c)，表明边跨桥墩塑性耗能占比大于中跨桥墩，达到67.56%，钢管和混凝土塑性耗能分别为28.65%和71.35%，混凝土塑性耗能大于钢管；③桥墩和组合钢箱梁的塑性耗能见图14(d)，该刚构桥总塑性耗能为1 381.2 kJ，组合箱梁和桥墩占比分别为68.1%和31.9%，表明墩强梁弱。

图14 地震作用下刚构桥各构件的塑性耗能占比

图15～图18分别为400 Gal地震作用下双重组合作用、地震作用方向、桥墩高和截面尺寸对刚构桥梁和柱耗能分配机制的影响，可知：①箱梁底板布置栓钉和混凝土后形成双重组合作用可增大组合箱梁的塑性耗能；②地震波沿横桥向和顺桥向作用，两者均以组合箱梁耗能为主，且顺桥向的组合箱梁的塑性耗能比值大于横桥向，顺桥向由于各桥墩柱和组合箱梁之间的相互作用，刚度较大进而各塑性耗能值较小；③随着桥墩高度的增大，桥墩占刚构桥塑性耗能的比例增大，组合箱梁占比减小，表明桥墩越低其刚度越大，在地震中以组合箱梁耗能为主；④桥墩截面越大，可以提高刚构桥总塑性耗能和桥墩塑性耗能。

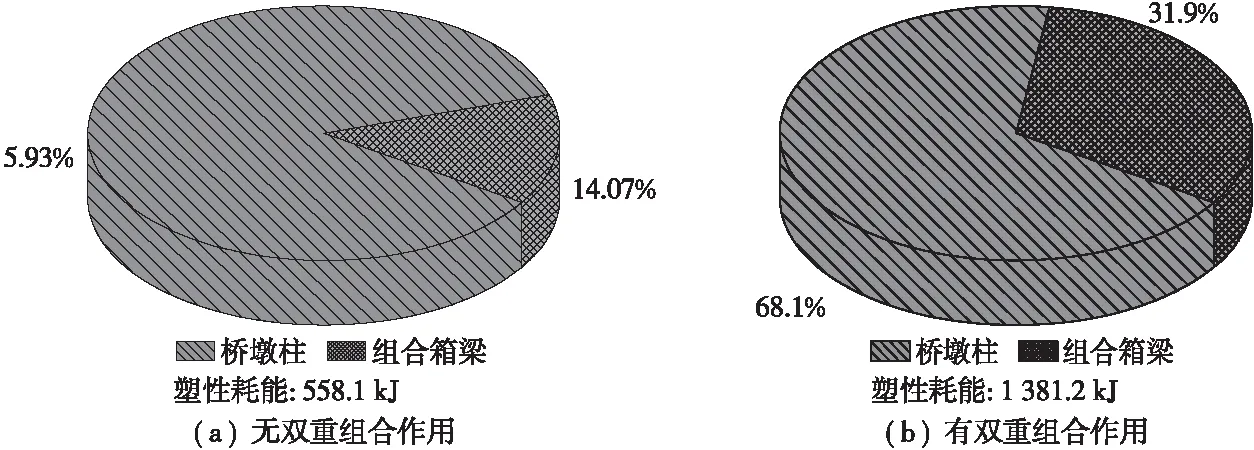
图15 双重组合作用对梁和墩塑性梁耗能的影响

图16 地震作用方向对梁和墩塑性耗能的影响

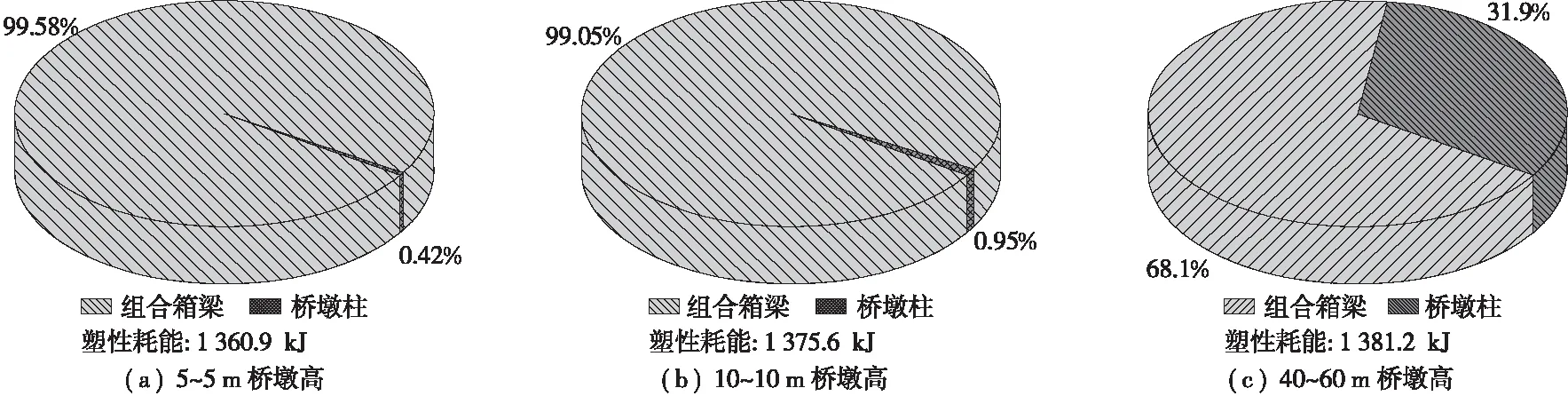
图17 不同墩高对刚构桥塑性耗能的影响

图18 不同墩截面对刚构桥塑性耗能的影响

5 结论

本文运用ABAQUS有限元软件对钢-混凝土组合箱梁连续刚构桥三维实体模型进行了地震动力弹塑性时程分析，主要结论如下：

a.地震烈度越大，其水平位移、加速度和墩底剪力等地震响应越大；桥面板中心的水平位移和加速度比边跨、中跨桥墩柱顶大，边跨桥墩柱底的剪力比中跨墩底大，且墩底剪力-墩底水平位移曲线均表现出良好的滞回性能。

b.对于组合箱梁，中跨墩顶负弯矩处和跨中位置处应力较大，箱梁双重组合作用效果更明显，而边跨墩顶位置处应力较小；对于桥墩，边跨桥墩墩顶、墩底和中跨桥墩墩顶、墩底处应力较大，伴随钢管屈服和混凝土被压碎，同时钢管表面的横向变形系数最大达到0.98，表明钢管对混凝土产生较强的约束，建议对桥墩支座、下部区域增加构造措施以加强桥墩抗震能力。

c.通过对刚构桥的塑性耗能分析表明，横桥向的地震塑性耗能高于顺桥向，箱梁的双重组合作用可以增大刚构桥塑性耗能，墩高越高、墩截面越大，桥墩的塑性耗能占比就越大。