大跨悬索桥主缆钢丝腐蚀后可靠性能评估
2023-01-16徐世桥马如进陈艾荣钟仁亮
徐世桥,马如进,陈艾荣,钟仁亮
(1.中国建筑第八工程局有限公司,上海 200122; 2.同济大学 土木工程学院,上海 200092)
1 概述
随着桥梁设计和计算理论的发展与施工建造技术的提高,现代桥梁正朝着复杂大跨的方向发展。从上世纪90年代开始,我国桥梁建设取得了世人瞩目的成就,先后建成了江阴大桥、西堠门大桥、泰州大桥、港珠澳大桥等多座复杂的千米级缆索承重桥梁[1]。随着越来越多的大跨桥梁投入运营,桥梁工程研究的科学问题也逐渐从设计理论、建造方法转移到运维管养研究[2]。特别是,大跨悬索桥结构造价昂贵,投资规模大,在其长达百年的服役期间,环境侵蚀、材料老化和荷载的长期效应,极易导致其技术状况呈下降趋势,从而影响桥梁的正常运营,甚至发生严重的安全事故,造成巨大的经济损失和人员伤亡。主缆是大跨悬索桥的主要承重构件,而腐蚀是影响主缆高强钢丝力学性能退化的主要原因[3]。悬索桥主缆钢丝的腐蚀与其内部的湿度有很大的关联,然而限于主缆内部钢丝的隐蔽性和现有检测技术的局限性,管理人员往往无法完全掌握内部钢丝的真实技术状态。虽然主缆由护套等防护系统包裹防止其内部钢丝腐蚀,但主缆从架设完成至最后的紧缆过程中会经历各种天气,从而导致完工后的主缆内部不可避免的存在水分。主缆钢丝腐蚀严重时会发生断丝,几乎所有大跨悬索桥都存在由于主缆钢丝腐蚀引起强度损失问题,严重的甚至已危及到桥梁的安全性能[4-5]。日本、美国等对其早期建设的部分悬索桥主缆进行了开缆检查,检查结果表明运营一段时间的主缆,其内部钢丝均存在一定程度的腐蚀。1989年日本对运营6 a的因岛大桥主缆进行开缆,检测发现主缆底部存有积水,主缆外围的钢丝出现明显的腐蚀,而且外层钢丝比内层腐蚀严重[6]。1996年美国对早期修建的几座悬索桥主缆进行了详细地检测,检测结果表明:美国大量的悬索桥包括Bear Mountain桥、Williamsburg桥、Brooklyn桥等都存在一定的强度损失问题,常见的情况是外层钢丝腐蚀严重,越往内层腐蚀逐渐减少[7]。
针对腐蚀后钢丝的性能退化和主缆性能评估等问题,国内外学者进行了一系列的理论与试验研究。曾严红等[8]通过静力拉伸试验研究直流电流加速腐蚀钢绞线的力学性能,随着腐蚀程度的增大,钢绞线极限强度迅速减小。KARAMCI等[9]从一座腐蚀严重的高架桥中取下一些受腐蚀钢丝做拉伸试验,结果表明钢丝强度随着腐蚀度的加大而明显降低。CAMO[10]收集并分析了美国和其它各地30多座大跨度缆索承重桥梁的力学参数与相关信息,以最小相关性为指标提出了一套系统的缆索安全性能评估方法。李陆蔚[11]借助室内试验模拟钢丝的腐蚀,提出了一种概率方法来估计缆索钢丝的残余强度。缆索钢丝腐蚀导致的性能退化问题是全世界关注的一个热点,也是一个世界性的难题。因为,钢丝容易与它所处的环境介质之间发生物理、化学和电化学作用,在潮湿环境下受到腐蚀影响,其可靠性不仅与钢丝自身性能相关,还与钢丝的荷载效应有着很强的相关性。因此,对钢丝发生腐蚀后主缆的可靠性进行评价,必须将主缆承受的外力与内部钢丝腐蚀后可以提供的抗力进行结合。鉴于此,本文以某大跨悬索桥主缆为研究对象,通过试验获取不同腐蚀程度下主缆钢丝的本构关系,建立主缆抗力概率模型,结合大桥所承受的外部荷载与Rice外推理论,获取不同运营期主缆的荷载效应模型,最终应用可靠度理论获取主缆的时变可靠度,以对不同运营时间的主缆可靠性进行评价,并为大跨悬索桥主缆运营过程中的管养决策提供理论支持。
2 主缆时变抗力概率模型
2.1 依托工程
本研究依托工程为某大跨悬索桥,桥梁主跨1 650 m,北边跨578 m,南边跨485 m,主缆从北锚碇到南锚碇的通长索股有169股,每根索股由127根直径为5.25 mm,公称抗拉强度为1 770 MPa的高强度镀锌钢丝组成。主缆在架设时竖向排列成尖顶的近似正六边形,紧缆后主缆为圆形,主缆索股的组成和编号如图1所示。
2.2 钢丝加速腐蚀试验
主缆是由成千上万根钢丝组成的,各根钢丝在生产加工、存储运输过程中存在一定的差异,处于不同位置不同环境的钢丝遭受的腐蚀也不一致。此外,不仅各根钢丝的初始性能不可能完全一致,运营一段时间后的钢丝性能差异更加显著。因此,通过多对根钢丝的力学性能进行测试,并采用统计参数描述不同钢丝的变异性。对于钢丝的力学性能,需要通过腐蚀模拟试验得到腐蚀后钢丝材料并进行力学拉伸试验统计分析获得。在这其中,需要分析的关键参量是明确的,例如弹性模量、屈服应力、屈服应变、极限应力、极限应变等。
经过对各种室内加速试验方案的比选,最终选择电解加速腐蚀的试验方案对高强钢丝进行腐蚀试验,该试验方法可以较真实模拟出腐蚀后的形态。试验采用的高强钢丝与该大跨悬索桥的主缆钢丝一致。此外,该大桥实际运营中的主缆应变水平介于2 000×10-6与3 000×10-6之间,所以设计的腐蚀钢丝的应变为2 500×10-6。考虑到试验数据离散性,为保证数据的有效性,每组试件设置为3个,共48根试件。加速腐蚀池设计为半封闭的溶液槽盛,放浓度为5%的NaCl电解液,试验现场如图2(a)所示。根据相关试验的经验,本试验将加速腐蚀的时间设置为4 d,通过记录不同腐蚀天数后钢丝的形态如图2(b)所示。显然,随着腐蚀程度的增大,钢丝表面出现明显变化,截面面积不断缩小。

(a)加速腐蚀试验装置
《NCHRP Report 534》是关于悬索桥主缆健康检测和性能评估的权威著作,其通过对美国30多座悬索桥开缆检查,根据腐蚀钢丝截面损失的比例,将主缆钢丝腐蚀程度划分为4个等级(钢丝横截面损失分别为0~5%,5%~10%,10%~15%,15%~20%)[12]。显然,对实际运营的主缆开缆检查获取的结果最能体现主缆的真实状态。因此,为了与《NCHRP Report 534》的试验结果进行对比分析,将试验后的钢丝按照与其相同的腐蚀等级划分标准,将腐蚀后钢丝划分为4个等级(Ⅰ-Ⅳ),并通过室内试验获取了不同腐蚀状态下钢丝的力学性能参数。试验数据分析发现,不同腐蚀等级下的钢丝弹性模量、极限应力、应变与弹性极限应力均服从对数正态分布,不同腐蚀等级钢丝随机本构模型参数如表1所示。由表1可知腐蚀对于钢丝的弹性模量影响较小,但对钢丝的极限应力影响很大,腐蚀等级越高,钢丝的极限应力越低,离散性越大。

表1 不同腐蚀等级的主缆钢丝力学性能参数Table 1 Mechanical properties parameters of main cable steel wire with different corrosion grades参数弹性模量E/MPa弹性极限应变εe弹性极限应力σe/MPa极限应力σμ/MPa腐蚀等级均值u标准差σ均值u标准差σ均值u标准差σ均值u标准差σ等级Ⅰ-4.7590.002 611 71217.121 78517.85等级Ⅱ-4.7710.003 581 69233.841 76335.262×1054×104等级Ⅲ-4.8100.004 411 62748.811 68950.67等级Ⅳ-4.8740.005 821 52676.29157 578.75
2.3 腐蚀后钢丝本构模型
主缆钢丝无论是否腐蚀,其均存在完全弹性阶段与应变强化阶段。在弹性阶段,高强钢丝除了在有缺陷的部位基本表现出完全的弹性,在经过屈服平台后,进一步加载将使得高强钢丝进入应变强化阶段。因此,描述钢丝应力与应变之间本构关系一般采用如下式所示的四参数曲线弹塑性模型:
σ=Eε, ifσ<σe
(1)
(2)
(3)
其中,σ为钢丝应力;E为弹性模量;ε为应变;C为材料参数;εe为弹性极限应变;εμ为钢丝极限应变;σμ为极限应力。通过对四参数钢丝本构曲线模型分析,以及钢丝加速腐蚀试验结果,利用Matlab软件编写4个腐蚀等级的钢丝本构关系曲线随机生成程序,模拟生成各个腐蚀等级钢丝的本构模型曲线,所得的结果如图3所示。显然,不同腐蚀等级的钢丝模拟出的钢丝应力-应变曲线均存在完全弹性阶段与应变强化阶段,且腐蚀等级越高,钢丝的极限应力越小。

图3 主缆钢丝腐蚀后本构模型曲线
2.4 主缆抗力时变模型
主缆抗力模型的建立,主要是基于蒙特卡洛理论,随机产生169×127=21 463个数据,每产生一个随机数(代表一根模拟的钢丝)其落在每层索股中(图1中的索股层编号1-6)的概率按照每层索股数的比例进行确定,即1~6层分别为:24.85%,21.30%,17.75%,14.20%,17.75%,4.15%。此外,由于不同索股层的湿度不同,其内部钢丝处于每个腐蚀等级的比例也存在差别,越外层的索股其内部钢丝腐蚀越严重(即处于高腐蚀等级的钢丝占比高),而越往内部索股层钢丝腐蚀程度越轻(即处于高腐蚀等级的钢丝占比低)。由此,可根据《NCHRP Report 534》中给出的处于不同运营时间时,各索股层中各个腐蚀等级钢丝的比例,将不同运营时间的主缆等效抗力频数与生成的各腐蚀等级的钢丝本构模型进行综合。通过上述分析,计算获得的不同运营年限时主缆的抗力时变模型,如图4所示。显然,不同运营年限时主缆抗力概率分布模型均符合正态分布,但随着运营年限的不断增长,主缆抗力均值逐渐减小,离散性逐渐增大,说明腐蚀对主缆的抗力产生了显著影响。
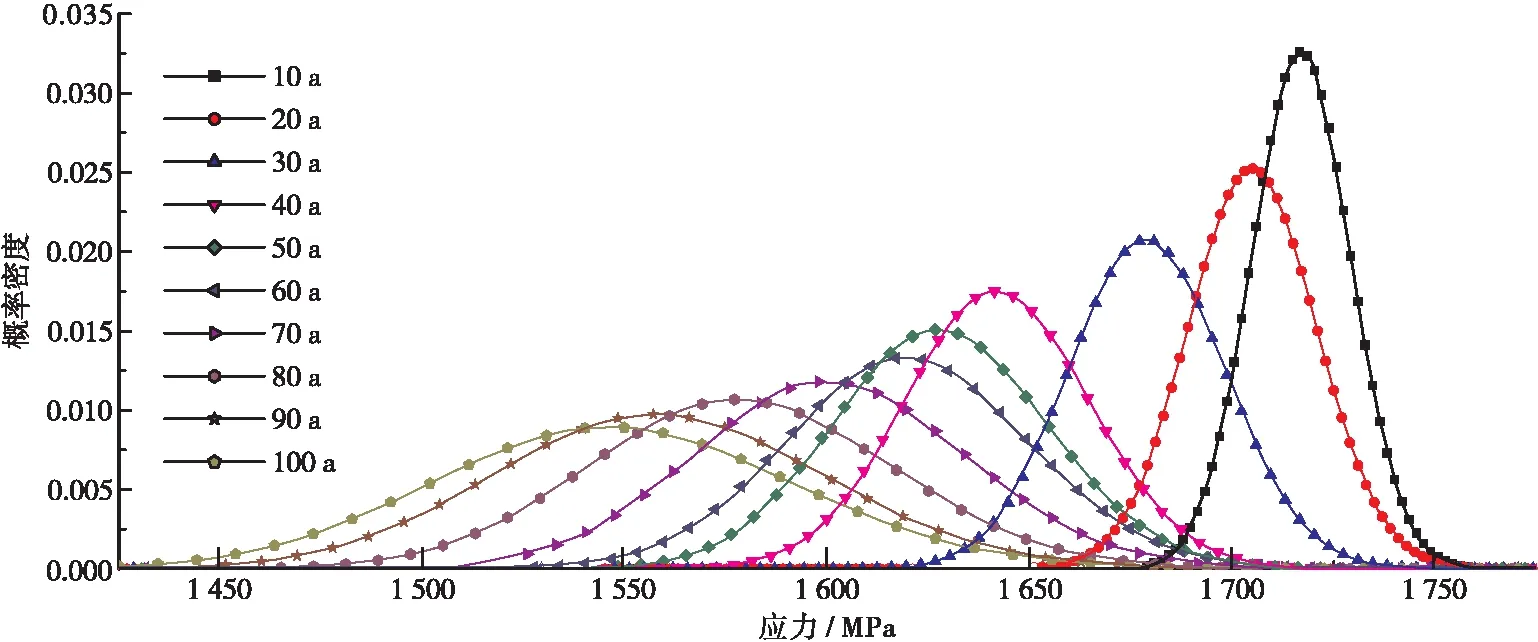
图4 主缆时变等效抗力概率模型
3 主缆荷载效应概率模型
3.1 荷载作用下主缆应力
桥梁在运营过程中主要承受温度荷载、风荷载,以及车辆荷载。根据《公路桥涵设计通用规范JTG D60—2015》中对承载能力极限状态的荷载组合规定[13]。本文采用的荷载作用效应组合式为:1.1×(1.2×恒载效应+1.4×车辆荷载效应+1.4×0.75×温度荷载效应+1.1×0.75×风荷载效应)。通过对该桥监测系统采集的不同工况的风荷载数据、温度荷载数据,以及动态称重系统采集的车辆荷载数据,将上述荷载分别施加到大桥有限元模型,可以获得多个工况下的主缆应力,其中部分工况的结果如图5所示。
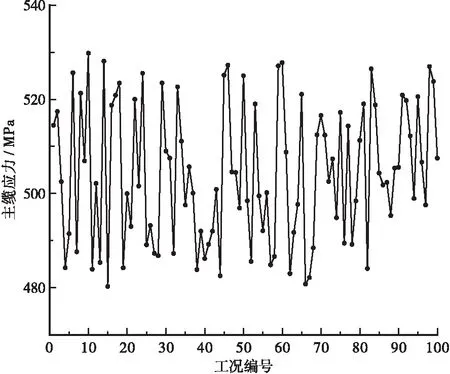
图5 外荷载作用下主缆应力响应
3.2 主缆荷载效应模型外推
为确定不同运营时期的主缆应力响应,并最终获取主缆应力响应的概率模型,必须将主缆应力响应进行外推。Rice外推理论起源于上世纪中叶,最初用于噪声的预测研究,直至1995年法国学者CREMONA[14]首次将Rice外推理论用于桥梁荷载效应的预测。对于大跨径桥梁,描述荷载效应随时间变化的随机过程X常被视作平稳高斯过程,部分较大跨径桥梁的车辆荷载效应亦被证明服从这一假定。对于满足高斯过程的荷载效应,可根据相应的时程曲线绘制水平穿越次数(频次)直方图,其穿越次数应满足式(4)所示的Rice公式,这一特点可以用于推断任意重现期内的荷载效应
(4)

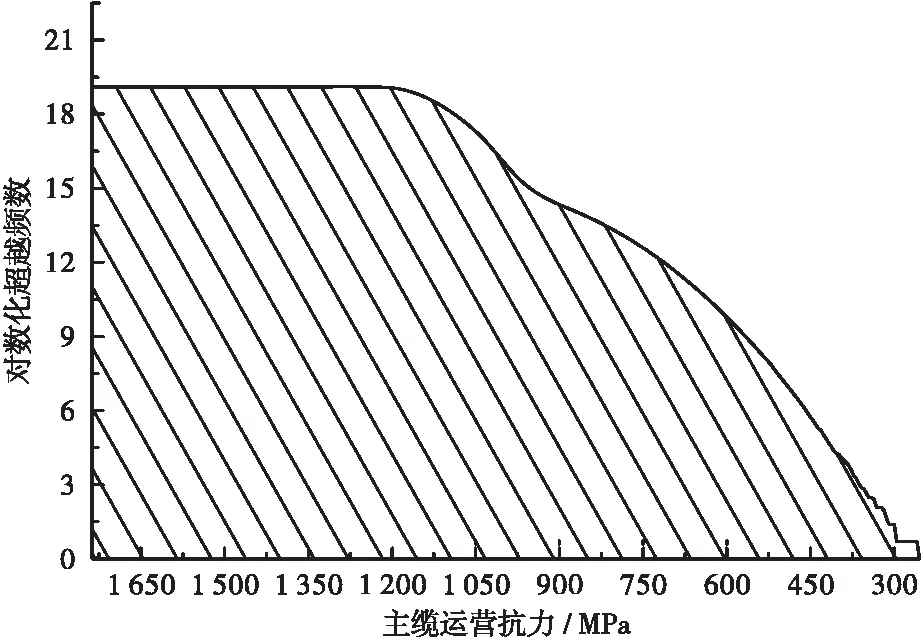
图6 主缆运营50 a应力响应对数化频数分布图
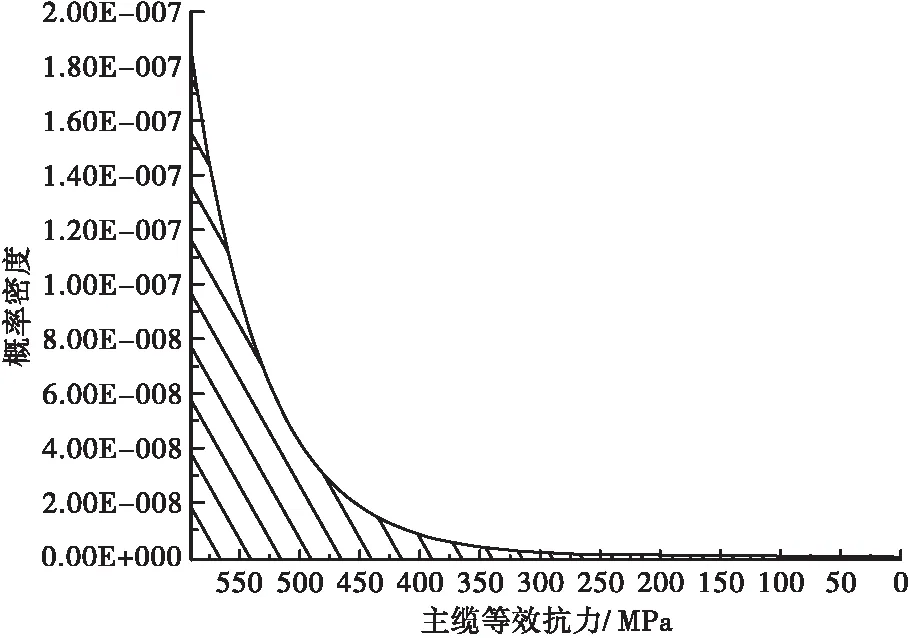
图7 主缆运营50 a荷载效应(应力)概率分布图
4 考虑腐蚀因素的主缆时变可靠度分析
对于结构而言能否满足功能要求主要是看结构可以提供的抗力R,能否满足各类荷载作用组合而形成的作用效应S,由此可以定义如式(5)所示的功能函数:
Z(R,S)=R-S
(5)
显然,对于大跨度桥梁主缆而言,荷载的不确定性会导致作用效应S的不确定性,由于钢丝腐蚀导致性能退化会引起结构抗力R的不确定性。可靠度理论充分考虑了结构在运营过程中荷载作用与抵抗力的诸多不确定性,并计算结构服役过程中无法满足功能要求的概率。因此,针对内部钢丝腐蚀后主缆的时变可靠度分析,其抗力R通过不同腐蚀等级钢丝的本构模型和其占比综合计算获得,而作用效应S分析中,采用Rice外推的方法对多种荷载组合作用下的主缆荷载效应进行分析。由此,可以构造功能函数并获得功能函数的概率分布,将功能函数小于零的部分进行数值积分后,可获得不同运营年限下的主缆构件失效概率,在此基础上得到主缆结构可靠度指数和其对应的失效概率随时间的变化规律,如图8所示。
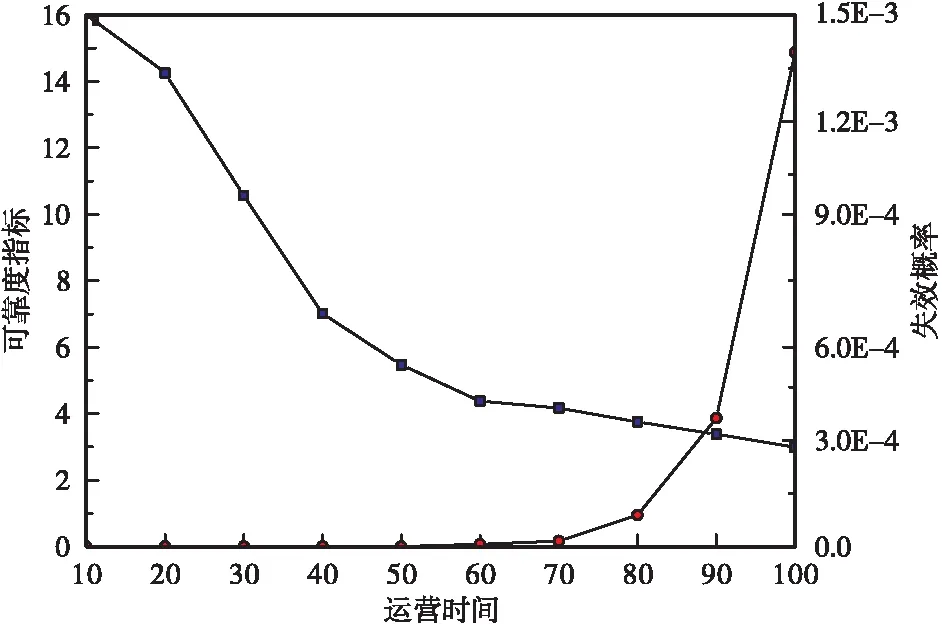
图8 主缆可靠度指标随桥梁运营时间变化规律
5 结论
针对大跨悬索桥运营期主缆钢丝腐蚀引起的主缆性能退化,可靠性降低的问题,结合钢丝腐蚀加速试验,建立了内部钢丝腐蚀后主缆的可靠性评估的方法,给出了大跨悬索桥主缆钢丝可靠性指标随运营时间的变化规律,主要结论如下:
a.通过设置电解加速腐蚀的试验,对主缆钢丝腐蚀进行模拟发现腐蚀后钢丝的弹性模量、弹性极限应变、弹性极限应力、极限应力等均符合对数正态分布,且腐蚀对于钢丝的弹性模量影响较小,但对钢丝的极限应力影响很大,腐蚀等级越高,钢丝的极限应力越低,离散性越大。
b.不同运营年限时主缆抗力概率分布模型均符合正态分布,但随着运营年限的不断增长,主缆抗力均值逐渐减小,离散性逐渐增大,腐蚀对主缆的抗力产生了显著影响。
c.主缆的可靠性与外部荷载引起的主缆荷载效应有关,外部荷载与桥梁有限元模型相结合可以获取荷载作用下主缆的应力响应,借助于Rice外推公式,可对不同运营时间时的主缆的荷载效应进行预测,进而可建立主缆荷载效应模型。
d.主缆不同运营时间下可靠性评估结果表明,主缆可靠度指标由10 a时的15.83下降至100 a时的2.99,对应的失效概率由9.66×10-57升高至1.4×10-3。因此,在大跨悬索桥日常运维管养中应采用适当的措施与设备(如主缆除湿系统),减缓或控制主缆内部钢丝的腐蚀。
