兼顾超低频振荡抑制和调频性能的自动发电控制参数优化
2023-01-14王雅军程杨帆聂强丁仁山王渝红朱杰
王雅军, 程杨帆, 聂强, 丁仁山, 王渝红*, 朱杰
(1.雅砻江流域水电开发有限公司, 成都 610051; 2.四川大学电气工程学院, 成都 610065)
直流异步联网工程投运以后,高水电占比直流送端电网的安全稳定运行风险由功角稳定问题转变为频率稳定问题[1]。例如,2016年3月28日云南电网异步联网试验期间发生振荡周期约为20 s的超低频振荡现象[1]。该振荡与水轮机调速器强相关,是一次调频过程小干扰不稳定的表现,退出水电机组一次调频后振荡平息,此类由机组一次调频引发的频率振荡被称为一次调频(primary frequency regulation, PFR)振荡模式[2]。2016年5月19日,云南电网发生由自动发电控制(automatic generation control, AGC)功率超调导致的超低频振荡现象,频率波动周期约在1 min[3]。该次振荡与AGC环节动作关系紧密,退出AGC环节后振荡平息,由电网AGC环节引发的频率振荡被称为AGC振荡模式[4]。
当前,关于PFR模式超低频振荡的产生机理、分析方法及抑制措施已有较多的研究。文献[5-7]指出水电机组的调速器响应过于灵敏及水锤效应产生的负阻尼是造成PFR模式超低频振荡的主要原因。为抑制PFR模式超低频振荡,文献[8-9]改进了电力系统稳定器结构用于实现对水电机组调速器的相位补偿,增加了调速器控制系统的阻尼;文献[7,10-12]分析了水电机组调速器参数对超低频振荡的影响,提出了通过优化大型水电机组的调速器参数抑制PFR模式超低频振荡的方法并在实际工程中得到有效应用。然而,调速器参数优化后水电机组一次调频能力下降,为缓解这一矛盾,文献[13-15]提出兼顾阻尼振荡与一次调频动态响应性能的综合优化方法并验证了其有效性。完整的电力系统有功频率控制包含一次调频与二次调频,上述文献均未考虑AGC环节。与抑制PFR模式超低频振荡前相比,水电机组一次调频能力仍有下降且伴随有发生AGC模式超低频振荡的风险,为保证送端电网的频率稳定,AGC控制系统肩负的责任更大[16]。
文献[3]提出了两种AGC模式抑制策略:一是调整AGC系统比例积分控制器的增益系数以降低调频机组的参与程度;二是调整AGC的调频模式,减少参与调频的发电机数目从而降低AGC的超调水平。该文献所提方法能有效抑制AGC模式超低频振荡,但缺乏对抑制机理的深层分析。文献[16]针对云南电网的AGC模式超低频振荡问题提出了用于高水电占比系统的B参数整定方法,该整定方法虽然有效地抑制了AGC模式的超低频振荡,但B参数整定过小导致扰动发生后频率恢复速度较慢,系统调频性能降低。文献[17]为提升AGC性能指标提出了基于AGC考核指标的控制器参数整定方法。文献[18-21]针对不同的运行场景改进互联电网的AGC系统控制器结构并使用智能算法对控制参数进行优化整定。上述文献所提出的AGC系统控制参数优化整定方法虽然能有效提高电网AGC的动态响应性能,但并未考虑AGC环节发生超低频振荡的风险。
基于上述背景,为了解决高水电占比送端电网的AGC模式超低频振荡问题,现参考文献[22]提出兼顾AGC模式超低频振荡抑制和二次调频性能的AGC系统控制参数整定方法。首先,建立高水电占比送端电网的负荷频率控制模型,基于该模型分别推导系统一次调频环节和AGC调频环节的传递函数,并使用参数根轨迹法分析AGC系统控制参数对全系统小干扰稳定性的影响。在此基础上定义表征超低频振荡风险的特征阻尼系数CDI,提出以CDI和时间绝对偏差乘积积分(integral of time multiplied absolute error, ITAE)为综合目标函数的AGC系统控制参数优化模型并采用粒子群优化算法进行求解。最后,通过算例分析从系统主导特征根、阻尼水平以及动态性能3个方面验证本文方法的有效性。
1 AGC模式超低频振荡分析
1.1 负荷频率控制模型
为了分析AGC模式的超低频振荡,首先建立系统负荷频率控制模型(图1)。该模型由调速系统、水轮机、等值发电机和AGC系统4部分组成。其中,调速器采用经典的GH型调速器简化模型,包含调差系数倒数Ggov1、控制等效环节Ggov2两部分,如式(1)和式(2)所示;原动机选择水轮机模型,如式(3)所示,式(4)是等值发电机数学模型。式(2)~式(4)是以复频率s为自变量的函数。
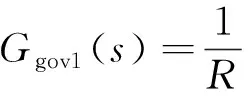
(1)
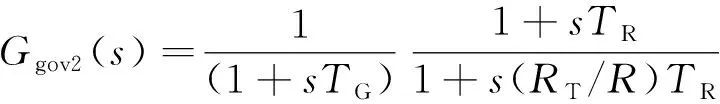
(2)
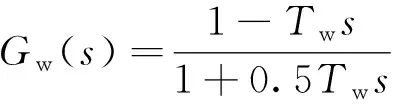
(3)
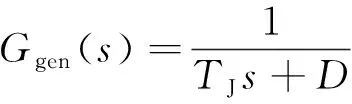
(4)
式中:R为一次调频调差系数;TG、TR、RT分别为调速器响应时间常数、软反馈时间常数和软反馈环节系数;Tw为水流惯性时间常数;TJ为发电机惯性时间常数;D为机组阻尼与负荷频率调节效应之和;ΔPL为系统负荷变化量。
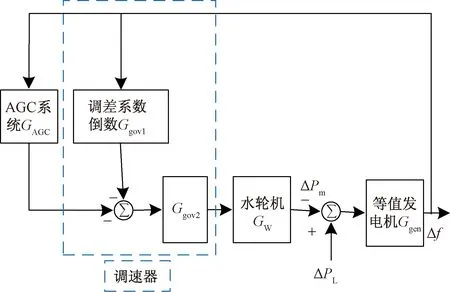
图1 负荷频率控制模型Fig.1 Load frequency control model of the sending power system with high proportion hydropower
AGC模型的结构如图2所示,包含:B系数模块、PI控制器、延时环节和零阶保持器。频率响应系数B受电源结构、调速器及负荷等因素的影响,由电力系统固有的频率响应特性决定[22];PI控制器用于系统功率调节量的计算,包含Kp和Ki两个控制参数;延时环节和零阶保持器分别对应AGC系统信息延迟及控制周期,其中τ、T分别代表信息传输延迟时间和AGC系统控制命令周期;ΔPm为水轮机输出机械功率的变化量;Δf代表系统频率偏差。

图2 AGC结构图Fig.2 Structure of AGC system
模型中,AGC系统采用定频率控制(flat frequency control, FFC)模式,输入信号Δf是送端电网的频率偏差。区域控制偏差(area control error, ACE)的计算公式为
ACE=B(fa-fs)=BΔf
(5)
式(5)中:fa为电网实际频率;fs为电网额定频率。
假设AGC环节无频差死区,一次调频环节频差死区为±fdb,系统频率控制满足以下要求[23]:①机组执行AGC调节命令时不受一次调频的影响;②一次调频动作过程中若有新的AGC命令,机组应立即执行AGC调节命令;③在没有新的AGC调节命令且一次调频正在动作时,一次调频正常动作。
1.2 AGC控制参数对系统小干扰稳定性的影响
超低频振荡是系统小干扰不稳定的表现,使用特征值法可以对系统的稳定性进行判断。PI参数是AGC系统重要的控制参数,因此有必要分析PI参数对AGC环节小干扰稳定性的影响。
首先,使用pade展开将AGC系统的延时环节和零阶保持器线性化,线性化后的AGC结构如图3所示,并写出AGC系统的传递函数,如式(6)所示。

图3 线性AGC结构图Fig.3 Structure of linearized AGC system
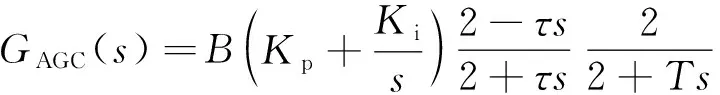
(6)
式(6)中:t为信息延迟时间;T为AGC系统控制命令周期。
由于一次调频环节设有死区±fdb,因此频差处于不同范围时有不同的控制器参与调频。当|Δf|
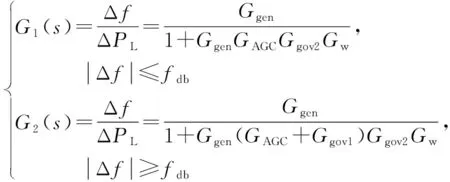
(7)
1+GgenGAGCGgov2Gw=0, |Δf|≤fdb
(8)
1+Ggen(GAGC+Ggov1)Ggov2Gw=0, |Δf|≥fdb
(9)
通过求解式(8)和式(9)的特征值可以分析不同频段下系统的小干扰稳定性。若特征值均为负,则说明系统在运行点是渐近稳定的;若至少存在一个为正的特征值,说明系统在运行点处不稳定。
参数根轨迹分析可以直接看出参数变化对系统小干扰稳定性的影响趋势[24]。基于线性化负荷频率控制模型分析AGC控制参数对全系统小干扰稳定性的影响,采用的初始参数如表1所示。由于是在调速器参数优化后的基础上研究AGC模式超低频振荡,因此一次调频环节是稳定的,AGC环节的失稳必然会对整体系统的稳定性产生消极影响。分别改变AGC系统PI控制器的比例系数Kp和积分系数Ki,不考虑一次调频死区,通过求解式的主导特征根,即可画出Kp参数和Ki参数的根轨迹图,结果如图4所示。
由图4看出,主导特征根随着Kp、Ki参数的增大逐渐向右复半平面移动,系统整体稳定性下降。由此说明,AGC系统控制参数设置过大不利于维持系统的小干扰稳定性,系统发生超低频振荡的风险将增大。
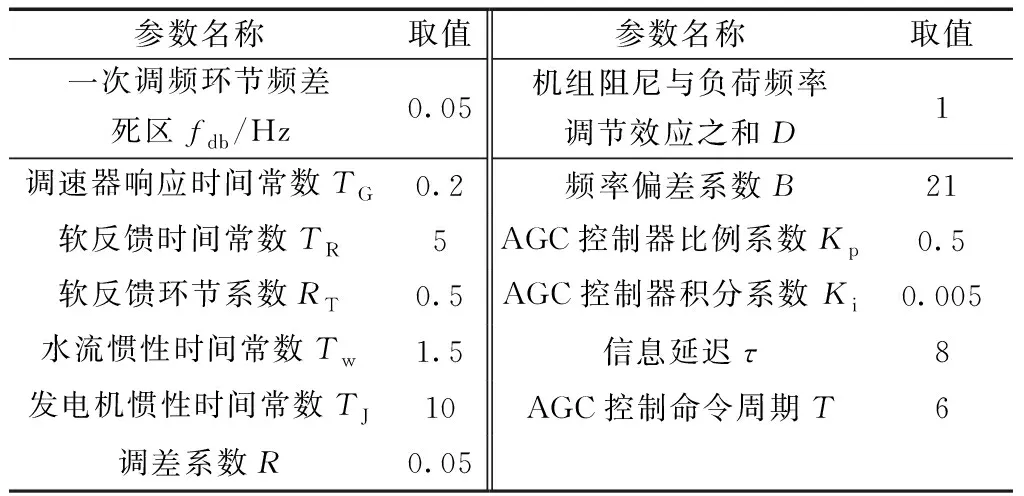
表1 负荷频率控制模型参数初始取值
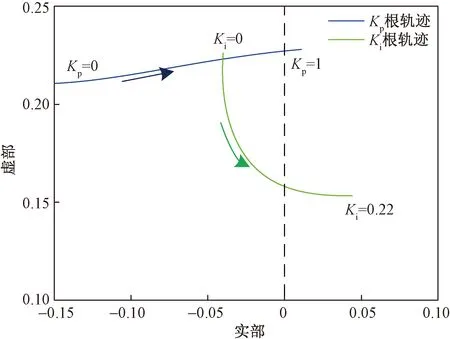
图4 PI参数根轨迹图Fig.4 The root locus of PI controller’s parameters
异步联网后,高水电占比送端电网频率稳定问题突出,增大AGC系统控制参数能改善电网二次调频性能,但同时也增大了系统发生超低频振荡的风险。因此,AGC系统控制参数的设计需兼顾考虑其调频性能和抑制AGC模式的超低频振荡。
2 基于PSO算法的AGC系统PI控制参数优化方法
2.1 优化目标分析
为了在设计AGC控制参数时兼顾考虑AGC调频性能和抑制AGC模式超低频振荡的需求,本文研究中建立如式(10)所示的综合优化目标函数。该综合优化目标函数由两部分组成:一部分是衡量系统阻尼水平的特征阻尼系数CDI;另一部分是衡量AGC调频性能的ITAE指标,k1、k2分别是两个指标的权重系数,其取值与优化目的的侧重选择、仿真时间长短有关。优化AGC系统PI控制参数即在搜索空间中寻找一组PI参数可以使目标函数值J最小。
minJ=k1CDI+k2ITAE
(10)
(1)特征阻尼系数CDI。求解式(8)得AGC闭环过程的各个特征根λi,进而由λi的实部σi和虚部ωi可求出每个特征根λi对应的阻尼比ξi。基于ξi定义CDI指标,其计算公式为
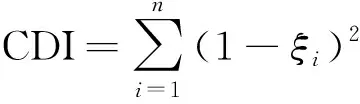
(11)
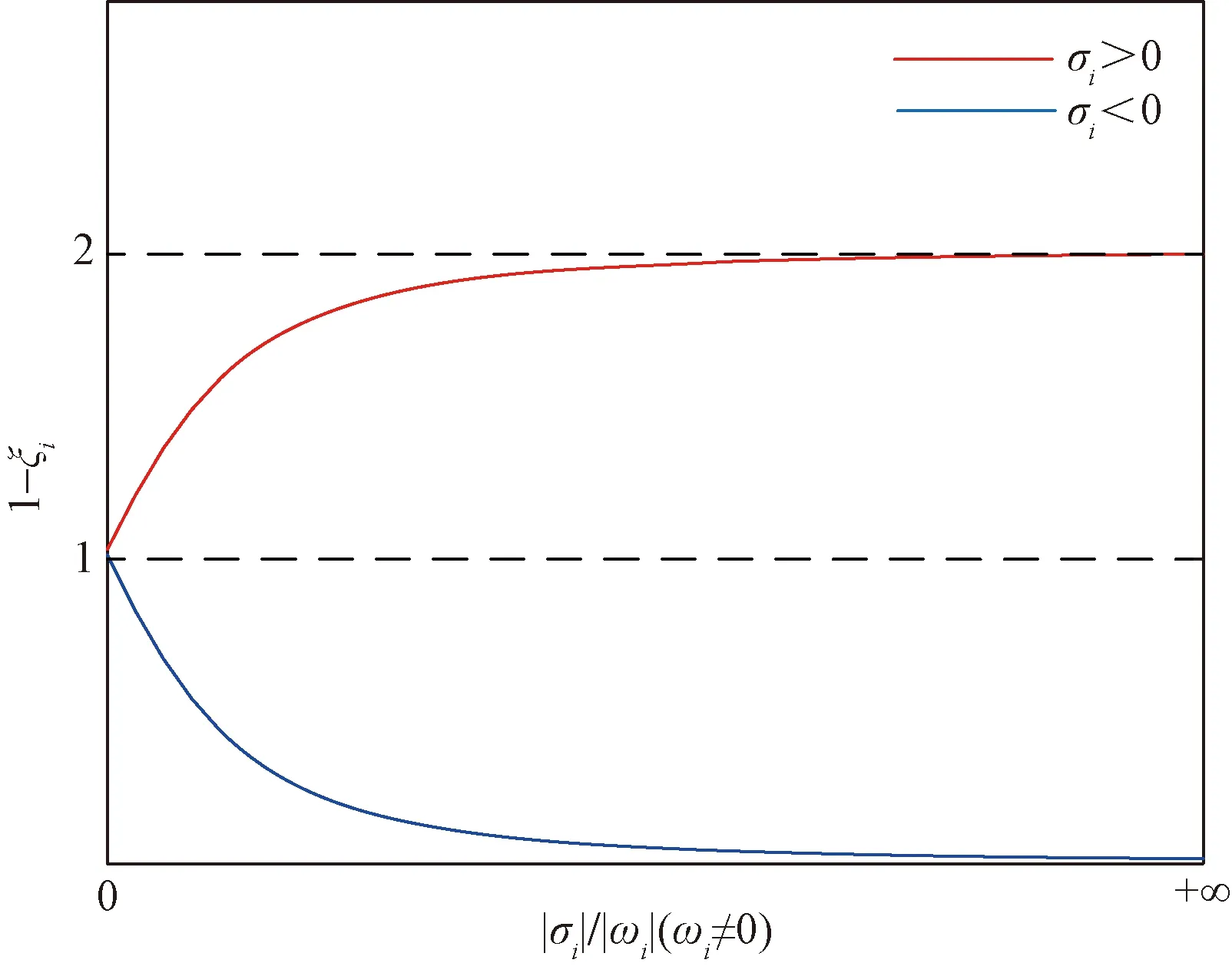
图5 (1-ξi)变化特性Fig.5 The characteristic of (1-ξi)
观察图5,CDI指标分析如下:①σi≤ 0且ωi≠ 0时,ξi随着|σi|/|ωi|单调递增,取值范围为[0,1],因此1-ξi单调递减且取值范围为[0,1],(1-ξi)2数值减小;②σi≥ 0且ωi≠ 0时,ξi随着|σi|/|ωi|单调递减,取值范围为[-1,0]。1-ξi单调递增且取值范围为[1,2],(1-ξi)2数值放大;③ωi=0时,若σi< 0,ξi=1,1-ξi=0;若σi>0,则ξi=-1,1-ξi=2。
综上分析可知,为维持控制系统的小干扰稳定,系统的特征阻尼系数CDI应越小越好。
(2)偏差性能指标。自动发电控制系统需要对系统频率偏差进行控制,由于频率偏差的变化与时间有较大关联,因此选择ITAE指标作为目标函数中的偏差积分性能指标,即选用时间与输出信号Δf的绝对值乘积积分作为目标函数的一部分,具体的计算公式为
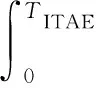
(12)
式(12)中:TITAE为仿真时间长度;t为时间变量。
此外,优化过程中PI控制器还应满足的约束条件如式(13)所示。
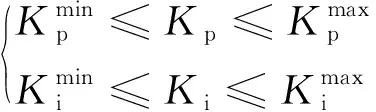
(13)
2.2 PSO算法原理
粒子群优化(particle swarm optimization, PSO)算法的基本思想是模拟鸟类的捕食行为,算法中的粒子通过对个体极值和全局极值的学习实现速度和位置的更新。粒子之间的相互学习使得该算法有较快的收敛速度,其全局搜索能力也较强。
假设在一个维数为D的搜索空间中有一个种群大小为N的搜索群体,设第i个粒子飞行的速度和位置为
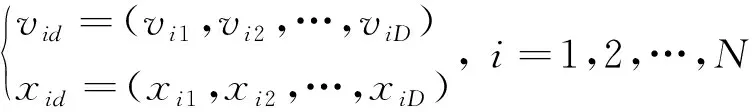
(14)
个体最优位置为
Pid=(Pi1,Pi2,…,PiD),i=1,2,…,N
(15)
全局最优位置为
Pgd=(Pg1,Pg2,…,PgD)
(16)
PSO算法中种群的每一次迭代都需要对粒子的位置和速度进行更新,更新的原理为
vid=wvid+c1r1(Pid-xid)+c2r2(Pgd-xid)
(17)
xid=xid+vid
(18)
式中:w为惯性权重;c1、c2分别为个体学习因子、群体学习因子;r1、r2为[0, 1]上的随机数字。此外,若自变量有取值范围要求,还需设置搜索空间范围x-limit。
2.3 优化算法流程
采用PSO算法对上述目标函数进行求解,优化计算流程如图6所示。具体步骤如下。
步骤1设置模型参数并初始化算法参数以及粒子种群的位置和速度。
步骤2计算各粒子的适应度。
步骤3在步骤2的基础上根据各个粒子的适应度值寻找个体历史极值并记录对应的位置与适应度值。
步骤4基于步骤3在所有个体极值中寻找全局极值。
步骤5根据公式、更新粒子的状态。
步骤6计算AGC闭环各特征值及特征阻尼系数CDI;计算AGC调频性能指标ITAE值。
步骤7判断主导特征根实部是否小于0及综合性能指标是否收敛。若满足结束条件,输出优化PI参数,算法结束;若不满足,回到步骤2。
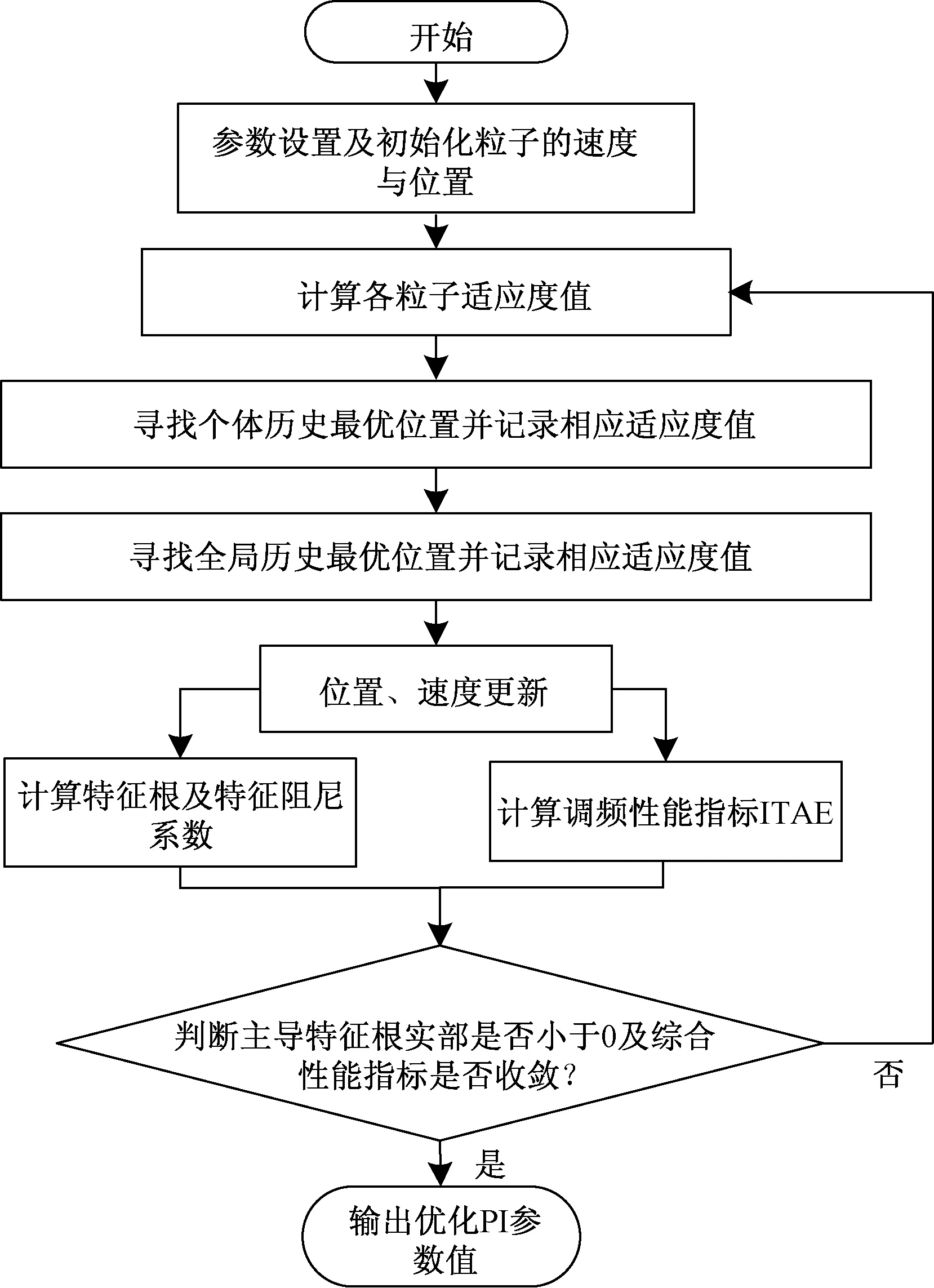
图6 优化算法流程图Fig.6 The process of optimization algorithm
2.4 算例分析
为验证所提方法的有效性,在MATLAB/Simulink中搭建了如图1所示的AGC系统仿真模型,模型参数设置如表1所示,PSO算法参数取值如表2所示。经上述参数优化方法寻优后,得到一组优化PI参数,分别是:Kp=0.095 983,Ki=0.001 663 2。下面从控制系统的主导特征根、AGC调频环节阻尼特性及动态响应性能3个方面做优化前后的对比分析。
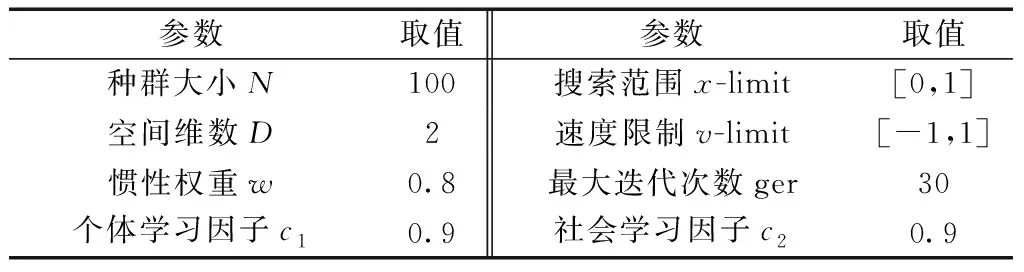
表2 PSO优化算法参数取值
2.4.1 系统主导特征根对比
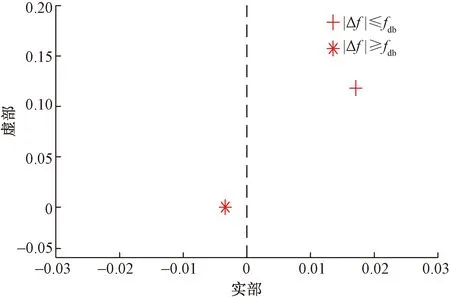
图7 不同频段的系统主导特征根(初始PI参数)Fig.7 The dominant characteristic roots of system (initial PI parameters)
基于表1求解式、得到初始PI参数下不同频段对应的系统主导特征根,如图7所示。从图7可知:当|Δf|≤fdb时,仅AGC参与频率调整,系统主导特征根实部为正,因此AGC闭环控制环节不稳定;当|Δf|≥fdb时,AGC与一次调频共同参与频率调整,主导特征根实部为负,系统是稳定的。
优化PI参数后不同频段的系统主导特征根如图8所示。可以看出,PI参数优化后不同频段的主导特征根实部均为负,不同控制器参与调频时系统均是稳定的。因此,从图7和图8的分析可得:优化AGC系统的PI控制参数能够有效提高AGC闭环控制环节的小干扰稳定性。

图8 不同频段的系统主导特征根(优化PI参数)Fig.8 The dominant characteristic roots of system (optimized PI parameters)
2.4.2 AGC调频环节阻尼特性对比
基于图1模型根据阻尼转矩法推导出仅AGC调频时发电机向系统提供的阻尼DAGC,具体的推导过程[25]为
已知发电机转子运动方程为
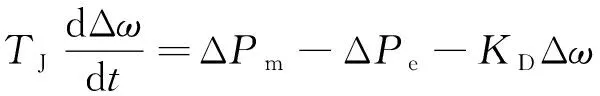
(19)
式(19)中:ω为发电机转速;KD为机组阻尼;Pe为电磁功率。其余参数前面已详细介绍,此处不再赘述。
由于原动机传递函数如式(20)所示,因此机械功率为
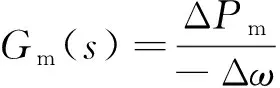
(20)
ΔPm=Gm(s)(-Δω)
(21)
将式(19)进行Laplace变换,令s=jω并把式(20)和式(21)代入式(19)中,得到
{Re[-Gm(jω)]-Re[Ge(jω)]-KD}Δω
(22)
从式(22)可看出,-Gm(jω)的实部与Re[Ge(jω)]、KD作用相反,而Re[Ge(jω)]+KD=D。因此,Re[Gm(jω)]和D的作用相同。当Re[Ge(jω)]>0,发电机提供正阻尼;Re[Ge(jω)]<0时,发电机提供负阻尼。系统总阻尼Dsum计算公式为
Dsum=Re[Gm(jω)]+D
(23)
仅AGC参与调频时,机械功率提供的阻尼DAGC计算公式为
DAGC=Re[Gm(jω)]
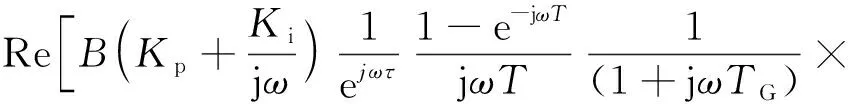
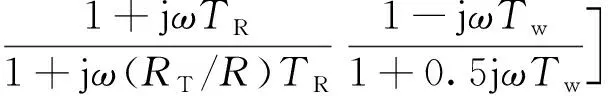
(24)
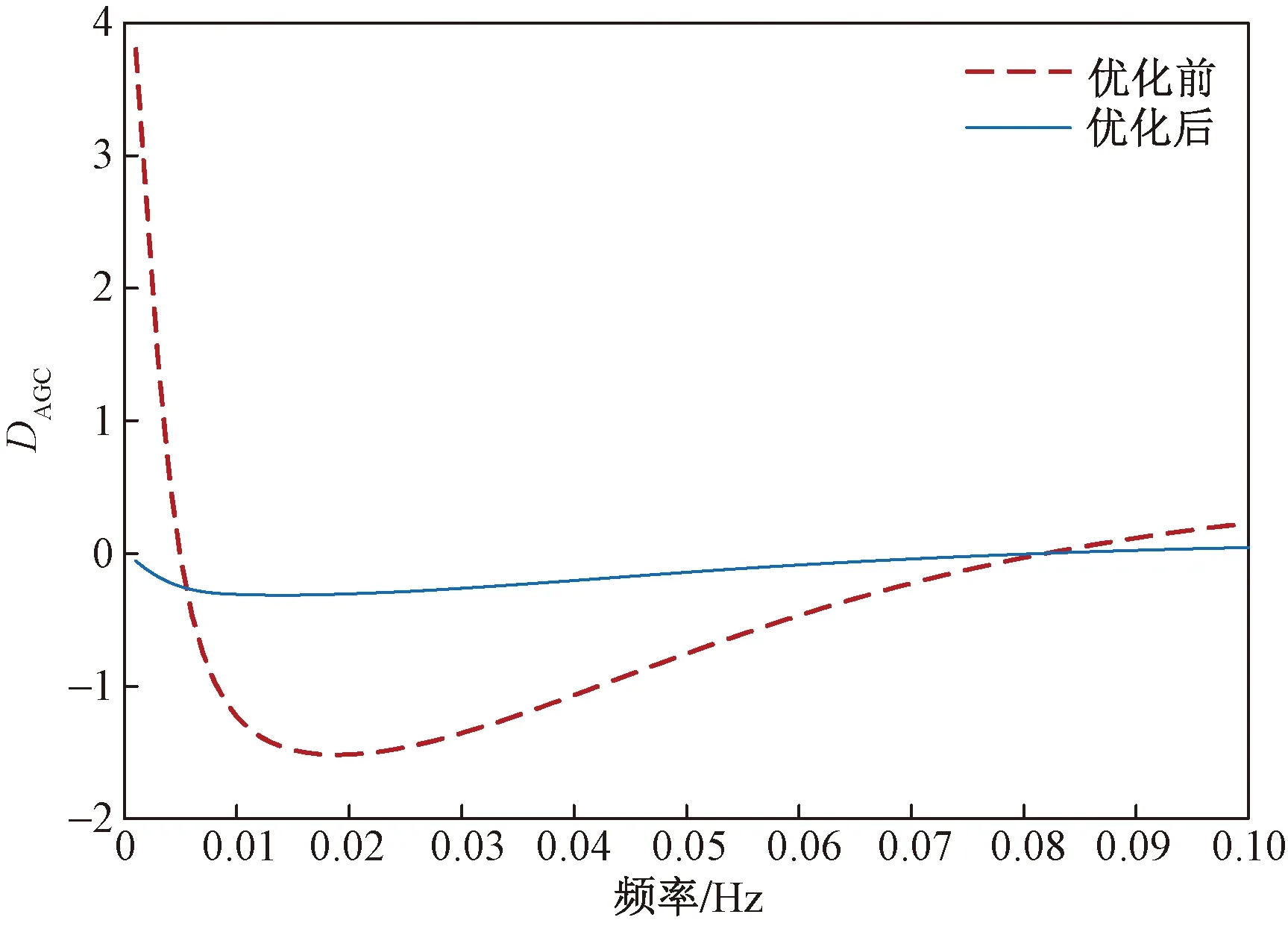
图9 优化前后AGC环节阻尼特性Fig.9 The comparison between initial damping characteristics and optimized damping characteristics of AGC
根据式(24)画出优化前后的DAGC曲线,如图9所示。图9中红色虚线为优化前的DAGC曲线,蓝色实线为优化后的DAGC曲线。
从图9可以看出:优化前,AGC调频环节在0.019 Hz时向系统提供最多的负阻尼,为-1.518;PI控制参数经本文方法优化后,AGC调频环节在0.014 Hz时提供最多的负阻尼,为-0.314 1。由此得到结论:PI控制参数经本文方法整定后,AGC调频环节向系统提供的负阻尼大大减小,达到了抑制AGC模式超低频振荡的目的。
2.4.3 动态响应性能对比
假设在负荷侧添加阶跃扰动,采用本文方法整定的PI参数,并与初始参数、文献[16]进行比较,结果如图10和图11所示。
图10、图11验证了图7的主导特征根分析。由图10看出,初始参数下,当|Δf|≤fdb时仅AGC参与频率调整,AGC闭环控制环节不稳定,受到小干扰时频率振荡发散。当频差振幅越过死区fdb后,一次调频参与频率调整,系统小干扰稳定,振荡被抑制,直到频差恢复至死区以内,系统再次不稳定,如此反复,系统频率表现为如图11红色实线所示的等幅振荡。由此可知,初始参数下,AGC环节不稳定引发AGC模式超低频振荡,二次调频不能实现无差调频。
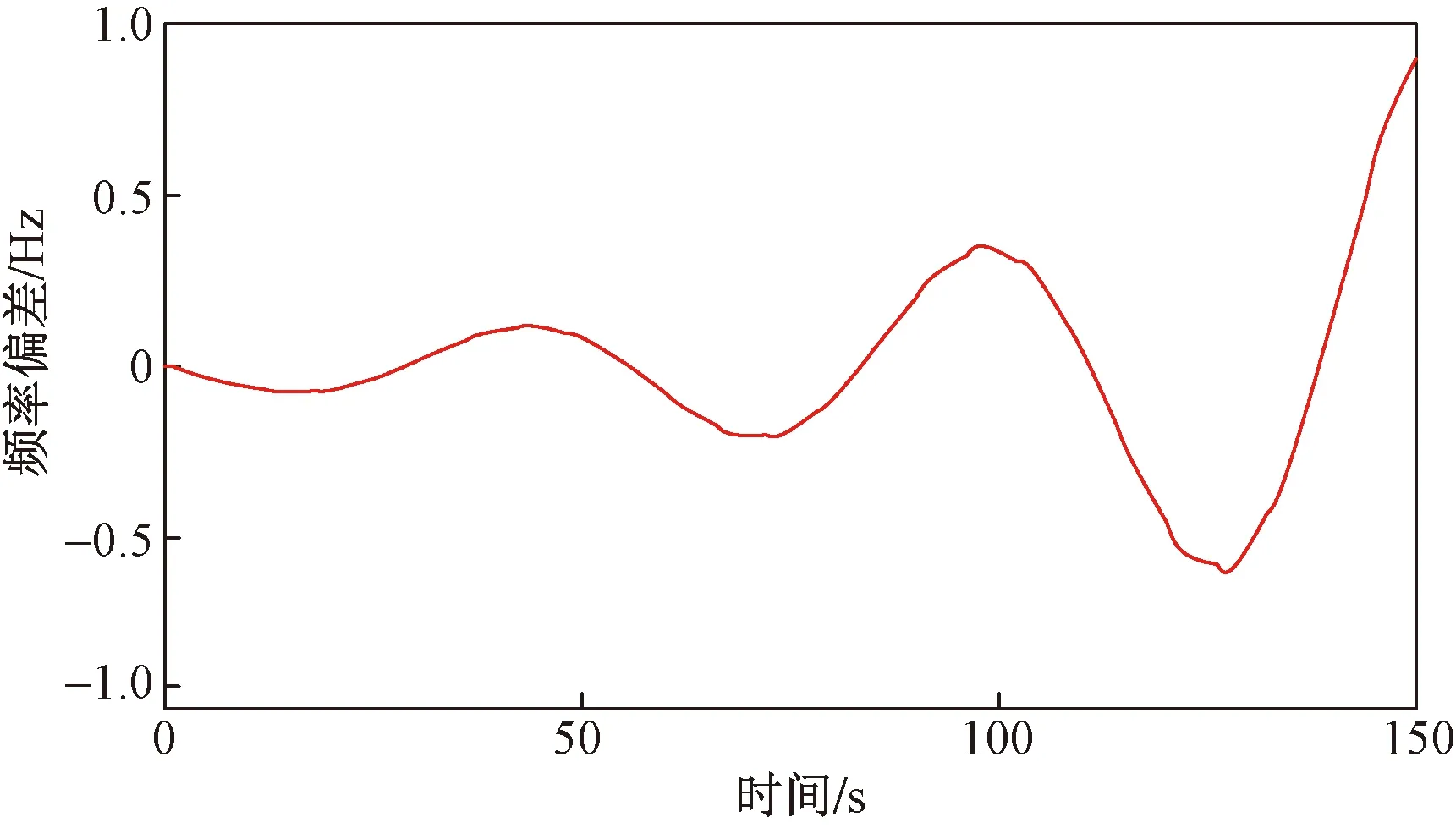
图10 初始参数下仅AGC调频系统频率偏差Fig.10 Frequency deviation of AGC withinitial parameters
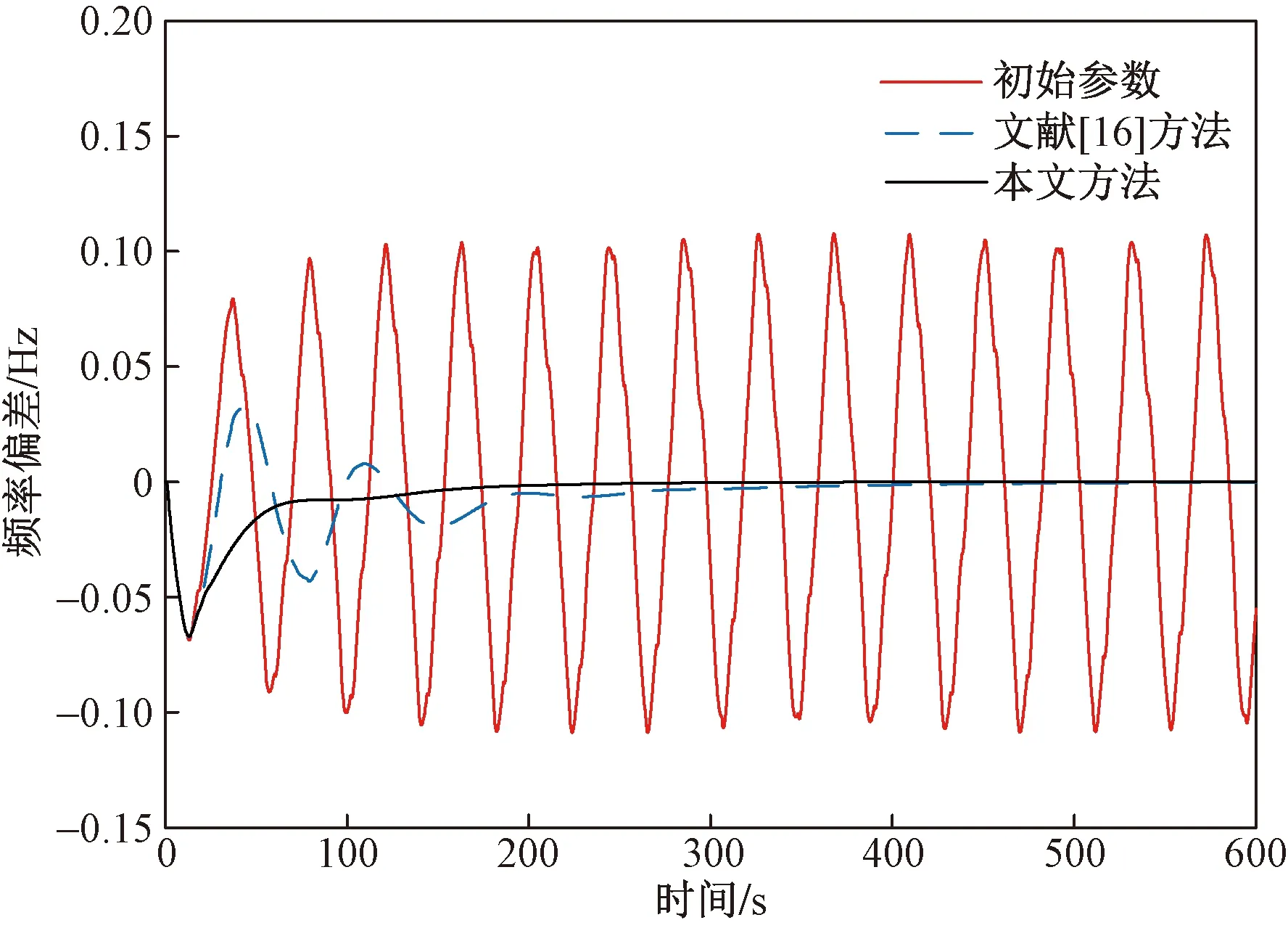
图11 不同参数整定方法下系统频率偏差Fig.11 Frequency deviation of AGC and PFR under different parameters’ setting methods
图11中黑色实线是采用本文方法整定的PI参数的仿真结果。可以看出,当系统受到扰动导致频差越过一次调频死区时,一次调频环节快速响应将系统频差控制在死区以内。系统频差不再越限后,一次调频环节退出频率调整,由AGC调整机组出力使频率恢复至额定值。与初始参数的仿真结果相比,本文方法设计的PI控制器能有效提升系统AGC闭环过程的小干扰稳定性,恢复二次调频的无差调节能力。此外,观察图11知,本文方法下系统频率经过232 s恢复至额定值,较文献[16]方法提高了46.67%。由此可得结论:相比于文献[16]方法,本文方法不仅提高了AGC环节的稳定性,而且能使系统频率更快速、平稳不振荡地恢复至额定值,有效地兼顾了AGC调频性能和抑制AGC模式超低频振荡两种需求。
3 结论
通过理论推导和仿真分析对AGC模式超低频振荡进行研究,并提出了相应的振荡抑制方法,得到如下结论。
(1)基于线性化负荷频率控制模型并使用参数根轨迹法分析发现,系统的小干扰稳定性随着AGC系统Kp参数、Ki参数的增大而降低。
(2)通过对不同频段下系统的主导特征根进行分析可知,AGC模式超低频振荡的实质是AGC闭环控制过程小干扰不稳定。
(3)定义了表征AGC环节阻尼水平的CDI指标,提出兼顾AGC模式超低频振荡抑制和调频性能的AGC系统PI参数优化方法。基于阻尼转矩法分析证明了经本文方法设计的PI控制器能有效减少AGC调频环节向系统提供的负阻尼,使振荡得到了有效抑制。并且与文献[16]相比,本文方法在提高AGC闭环过程小干扰稳定性的前提下频率恢复更平稳、恢复速度更快。
