由一道考研题引起的对随机变量独立性的探讨
2023-01-14刘可为宁荣健
刘可为, 宁荣健
(合肥工业大学 数学学院, 合肥 230601)
1 引 言
2022年全国硕士研究生入学统一考试数学一第10题为
引例设X~N(0,1),在X=x的条件下,Y~N(x,1),则X与Y的相关系数为( ).


所以
下面给出两种解法.
解法1由于二维正态分布的密度函数为

解法2由于X~N(0,1),则EX=0, DX=1,而
则Y~N(0,2),E(Y)=0,D(Y)=2.由于
所以X与Y的相关系数为
故选(D).
对于大多数考生来说,解法1的计算量虽然不大,但是其中二维正态分布的密度函数却难以记住,影响正常解题.作为填空题,解法2的计算量过大,不宜采用.
本文通过该问题中的有关独立性的讨论,给出本题方法简单,计算量适中的解题方法.
2 主要结论
引例中,在X=x的条件下,Y~N(x,1),可得Y-X=Y-x~N(0,1),表明Y-X的条件分布与X取值无关,能否由此断言X和Y-X相互独立?其答案是肯定的,给出下列定理.
定理1设函数z=z(x,y)具有一阶连续偏导数,且z′y≠0,y=y(x,z).X和Y为随机变量,X的密度函数为fX(x).如果对满足fX(x)>0的任意实数x,当X=x时,Z=z(X,Y)的条件密度函数fZ|X(z|x)与x无关,并记fZ|X(z|x)为g(z),则
(i)X和Z相互独立,且Z的密度函数fZ(z)=g(z);

证(i)记(X,Z)的密度函数为f(x,z),-∞
f(x,z)=fX(x)fZ|X(z|x)=fX(x)g(z), -∞ 对满足fX(x)=0的任意实数x,f(x,z)对z几乎处处为0,因此对任意(x,z)∈2,f(x,z)=fX(x)g(z)几乎处处成立.由于fX(x)dx=1,得g(z)=f(x,z)dx=fZ(z),故f(x,z)=fX(x)fZ(z)在2内几乎处处成立,所以X和Z相互独立,且Z的密度函数fZ(z)=g(z). (ii)由于X和Z相互独立,故由文献[1]定理2知Y的密度函数为 定理2设函数z=z(x,y)具有一阶连续偏导数,且z′y≠0,y=y(x,z).X和Y为随机变量,X的分布律为P{X=xi}=pi,i=1,2,….如果对满足pi>0的任意实数xi,当X=xi时,Z=z(X,Y)的条件分布律与xi无关,并将其记为P{Z=zj|X=xi}=qj,j=1,2,…,则 (i)X和Z相互独立,Z的分布律为P{Z=zj}=qj,j=1,2,…; (ii)记Y=y(X,Z)的取值为y1,y2,…,yk,…,Y的分布律为 证(i)记(X,Z)的分布律为 P{X=xi,Z=zj}=pij,i=1,2,…;j=1,2,…. 对满足pi>0的任意实数xi, pij=P{X=xi,Z=zj}=P{X=xi}P{Z=zj|X=xi}=piqj,j=1,2,…; P{X=xi,Z=zj}= P{X=xi}P{Z=zj}, 所以X和Z相互独立,Z的分布律为P{Z=zj}=qj,j=1,2,…. (ii)由于X和Z相互独立,故(X,Z)的分布律为 P{X=xi,Z=zj}=piqj,i=1,2,…;j=1,2,…, 进而得Y的分布律为 定理3设函数z=z(x,y)具有一阶连续偏导数,且z′y≠0,y=y(x,z).X和Y为随机变量,X的分布律为P{X=xi}=pi,i=1,2,….如果对满足pi>0的任意实数xi,当X=xi时,Z=z(X,Y)的条件密度函数fZ|X(z|xi)与xi无关,将其记为g(z),则 (i)X和Z相互独立,且Z的密度函数fZ(z)=g(z); 证(i)记(X,Z)的分布函数为F(x,z),X的分布函数为FX(x),Z的分布函数为FZ(z),-∞ 对满足pi=0的任意实数xi,P{X=xi,Z≤z}=0,所以对任意的i=1,2,…,-∞ P{X=xi,Z≤z}=P{X=xi}P{Z≤z}. 进而对任意的-∞ 即F(x,z)=FX(x)FZ(z),所以X和Z相互独立,Z的密度函数为fZ(z)=g(z). (ii)由于X和Z相互独立,故有 有了上面相关结论,再来看引例.记z=y-x,z′y=1≠0.由于在X=x条件下,Y~N(x,1),故Z=Y-X=Y-x~N(0,1),与x无关,所以由定理1(i)知X和Z相互独立,Z~N(0,1).进而由Cov(X,Z)=Cov(X,Y-X)=0,得Cov(X,Y)=DX=1.又Y=X+Z~N(0,2),DY=2,所以所求相关系数为 显然,利用本文结论既不需要利用解法1中难以记住的二维正态分布的密度函数,又避免了解法2中繁杂的计算. 例1(根据2004年全国硕士研究生入学统一考试数学四第23题改编) 设随机变量X~U(0,1),在X=x∈(0,1)的条件下,Y~U(0,x), (ii)求Y密度函数fY(y). 证法1(i)由于在X=x∈(0,1)的条件下,Y~U(0,x),故 所以 进而得 由于 (ii)由于 所以 (ii)由于X和Z相互独立,以及X~U(0,1),Z~U(0,1),由定理1(ii)知 例2(根据2015年全国硕士研究生入学统一考试数学一第22题改编) 设随机变量X的分布律为P{X=i}=p(1-p)i-1,i=1,2,…,在X=i(i=1,2,…)的条件下, P{Y=i+j|X=i}=p(1-p)j-1,j=1,2,…, (i)证明X和Y-X独立同分布; (ii)求Y的分布律. 证(i)记z=y-x,z′y=1≠0.由于在X=i(i=1,2,…)的条件下, P{Z=j|X=i}= P{Y-X=j|X=i}=P{Y=i+j|X=i}=p(1-p)j-1,j=1,2,… 与i无关,故由定理2(i)知X和Z相互独立,且Z的分布律为 P{Z=j}=p(1-p)j-1,j=1,2,…, 进而可知X和Z同分布,因此X和Z独立同分布,即X和Y-X独立同分布. (ii)由定理2(ii),得Y的分布律为 (ii)求Y的密度函数fY(y). 所以 本文主要讨论了X和Y为离散型随机变量和连续型随机变量的情形,如果X和Y中出现非离散型随机变量,也非连续型随机变量,是否仍有类似的结论?这个问题还需进一步研究,欢迎各位同仁给于指导,也期盼能共同探讨. 致谢感谢审稿人给出的宝贵意见,感谢唐烁老师对论文的结构等多方面的指导.
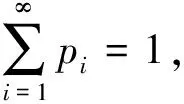


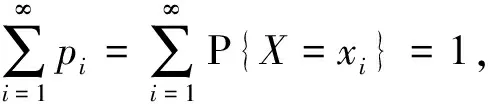
3 应用实例


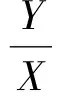






4 结束语
