利用惠更斯作图法解释渥拉斯顿棱镜的工作原理

吴许强

（安徽大学物理与光电工程学院，安徽合肥 230601）

自然光可利用偏振片（二向色性）、布氏角反射、玻璃堆透射、晶体双折射偏振器等原理与器件实现起偏[1]，其中晶体双折射器件使用光学纯的晶体，虽然价格昂贵，但因其出色的消光比、很高的激光损伤阈值，在光学调Q[2]、光谱学[3-4]、偏振成像[5-6]等领域中应用较多。其中，渥拉斯顿棱镜工作波长范围宽，是常用的晶体双折射偏振器之一。在赵凯华版《新概念物理教程光学》教材中，仅给出了渥拉斯顿棱镜的基础工作光路，并未对其结构、工作原理及其应用进行深入讲解，更未说明分离角和棱镜结构参数的量化关系，此章节学生常常难以理解，更勿提开展设计与应用。本文将使用惠更斯作图法，阐述寻常光（o光）、非寻常光（e 光）在晶体的走离机制与过程，解释渥拉斯顿棱镜的工作原理。

1 渥拉斯顿棱镜的结构

渥拉斯顿棱镜可以由两个同种材质的石英（SiO2）、方解石（CaCO3）或钒酸钇（YVO4）棱镜胶粘在一起制成，也可以有两个同种材质的氟化镁（MgF2）或偏硼酸钡（α-BBO）直接光学接触在一起制成[7-8]。直接光学接触比胶粘棱镜光学结构简单，且具有更高的损伤阈值，在超快激光中应用前景良好。图1为索雷博（Thorlabs）公司官网上封装前后渥拉斯顿棱实物图[8]。

图1 封装前后渥拉斯顿棱镜实物图

图2展示了渥拉斯顿棱镜的结构及光轴方向。渥拉斯顿棱镜第一块三棱镜光轴方向平行于入射界面，第二块三棱镜光轴方向垂直于入射光线和第一块三棱镜光轴构成的平面。以直接接触型渥拉斯顿棱镜进行分析，以负晶体（no＞ne,或ve＞vo）为例，采用惠更斯作图法，分析偏振光在棱镜内的传播规律。

2 在第一块三棱镜中光线的传播

假设有一束自然光（用上下两束平行光线表示）沿水平方向，垂直入射到第一块三棱镜，由于光轴方向平行于界面，会发生双折射，以下分别就o光和e光单独分析。

2.1 o光的波面、传播方向与偏振方向

由于o 光各向同性，其次波面为半球面，且经一定时间上下两根光线的半球型次波面半径相等，故其包络面为平行于界面的平面，连接次波源中心和切点并延长，得到o 光的传播方向，仍然沿水平方向没有改变。事实上，上述结果也可以由o光遵从普通的折射定律得到：入射角等于0，则折射角也等于0，光线正透射。根据主平面定义：o 光传播方向和光轴方向构成的面为o 光主平面，故此时纸面即为o 光主平面，又因为o 为线偏振光，且偏振方向垂直于o 光主平面，故o 光的偏振方向垂直于纸面，在图中用小圆点表示，也称为s偏振光。其次波面和偏振方向利用惠更斯作图法得到的结果如图2所示。

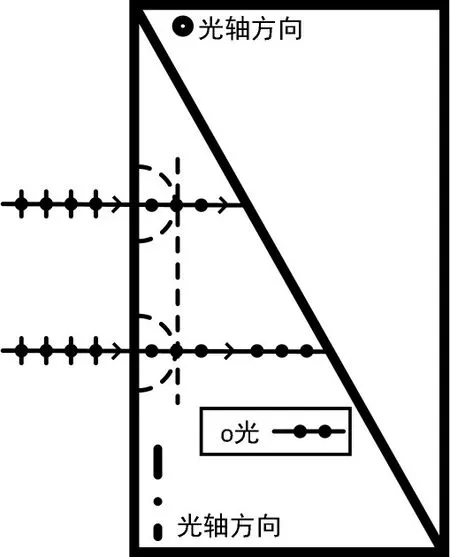
图2 第一块三棱镜中o光的传播

2.2 e光的波面、传播方向与偏振方向

e光在光轴方向（图示竖直方向）和o光的传播速度一致，在与光轴垂直的方向（图示水平方向）上传播速度为ve=，其次波面如图3所示的椭球面，竖直方向上与o光次波面相切，水平方向偏离最大。由于上下两根光线的次波面完全相同，故其包络面也为平行于界面的平面，故e光出射方向与o光一致，亦为水平出射。但由于是负晶体ve＞vo，e光的次波面较o光次波面超前。偏振方向方面，e 光传播方向和光轴方向构成的e光主平面，也为纸面。根据e光主平面性质，e光偏振方向平行于其主平面，故为平行偏振，称作p偏振光，在图上用垂直于光线方向的短线段表示。

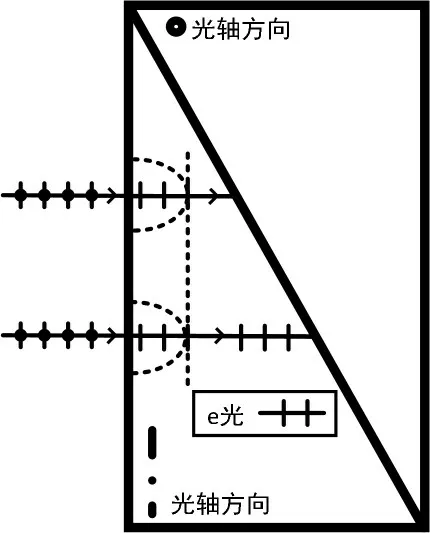
图3 第一块三棱镜中e光的传播

综上，当光线正入射到第一块三棱镜，由于光轴方向平行于界面，偏振光传播规律与波片类似：o 光和e光传播方向一致、不分开，但传播速度不一样，整体传播光路如图4所示。

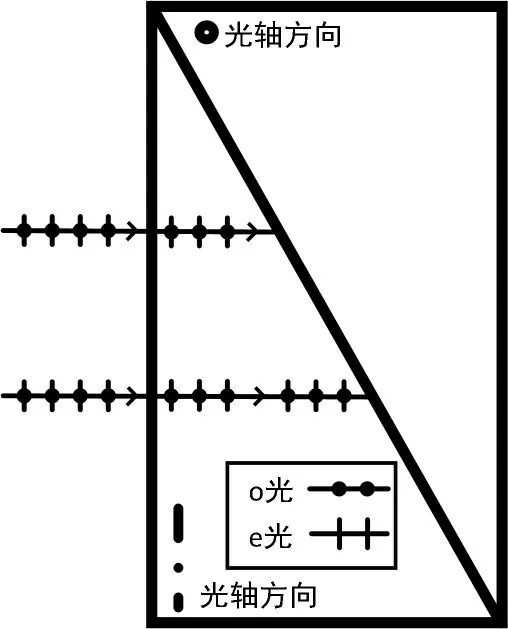
图4 第一块三棱镜中偏振光的整体传播

3 在第二块三棱镜中光线的传播

无论是第一块三棱镜中的s 偏振光还是p 偏振光，其光线方向均垂直于波面，即同时到达如图5 所示的AC 平面。第二块三棱镜的光轴方向垂直于纸面。由图可知，上光线先行达到两三棱镜交汇的棱边，即A 点，下光线还需传播几何长度方才到达棱边B 点。根据惠更斯原理，上光线达到A 时，先行发射球面次波。由于光轴方向垂直于纸面，故在纸面上，o 光、e 光的次波面均为圆形。

3.1 o光的波面、传播方向与偏振方向

对于第二块三棱镜中的o光，由于是负晶体其传播速度较小，球面次波的半径小于或者等于，可初步画出图5 中的半圆形次波面，过B 点作半圆的切线，设切点为D，BD 即代表第二块三棱镜中的o 光的次波面的包络面，即为新的波面。连接A、D 并延长，即为上光线o 光的出射方向。过B 点作AD 平行线，即为下光线o 光的出射方向。由于为o 光，其偏振方向应该垂直于其主平面（此时为通过BD，且垂直于纸面的面），故此时的o光为p偏振光，传播速度为vo。而p 偏振光在第一块三棱镜内表现为e 光，传播速度为ve，对负晶体，ve＞vo，故现可以确定o 光次波面半径应为小于而不是等于，此时的p 偏振光向上偏折。根据作图过程（含几何关系、波速与折射率的关系），有

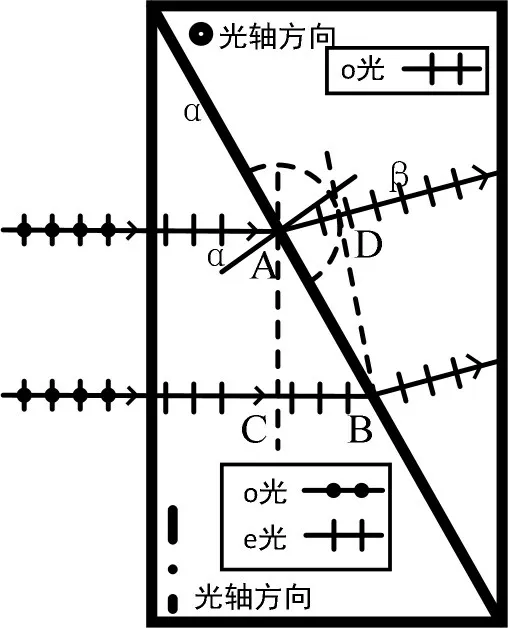
图5 第二块三棱镜中o光的传播

其中α代表三棱镜的顶角，亦为此时的入射角，β代表与界面法向的夹角，即出射角。出射光线与水平方向夹角为α-β。

3.2 e光的波面、传播方向与偏振方向

由于是负晶体ve＞vo，故在第二块三棱镜内，e光传播快，A点发出的次波波面的半径将大于或者等于，可初步画出图6中的半圆形次波面。类似地，过B 点作半圆的切线，设切点为E，BE 即代表第二块三棱镜中的e 光的次波面的包络面，即为新的波面。连接A、E 并延长，即得上光线e 光的出射方向。过B点作AE 平行线，即为下光线e 光的出射方向。同3.1，可以分析出第二块三棱镜中的e 光为s 偏振光，而s偏振光在第一块三棱镜中体现为o光。根据作图过程，有：

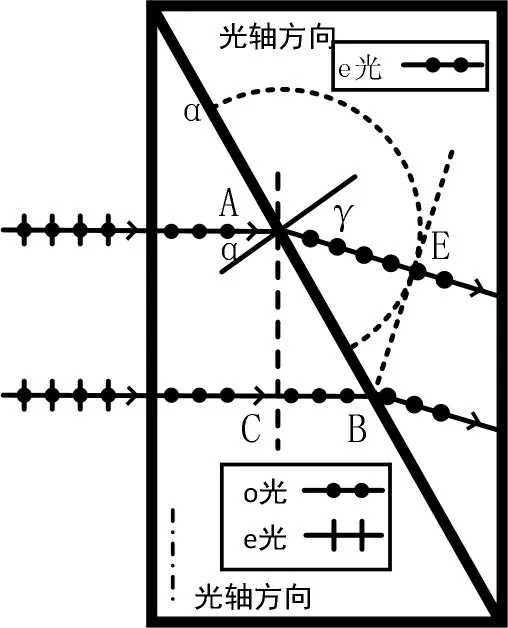
图6 第二块三棱镜中e光的传播

其中γ代表出射e 光与界面法向的夹角，即出射角。出射光线与水平方向夹角为γ-α。

综上，如果入射到晶体的为自然光，同时含有s和p 两个本征偏振态，进入晶体后即使发生了双折射，这两个本振偏振态不会互相串扰：s 线偏光在第一块三棱镜中体现为o光的传播规律，在第二块三棱镜中体现为e 光的传播规律；而p 线偏光在第一块三棱镜中体现为e光的传播规律，在第二块三棱镜中体现为o光的传播规律。本征偏振态的概念，对理解双折射至关重要，而该教材中对此鲜有表述。此外，从图7 可以看出，进入第二块三棱镜后，p 线偏光和s线偏光分别朝上和朝下走离。

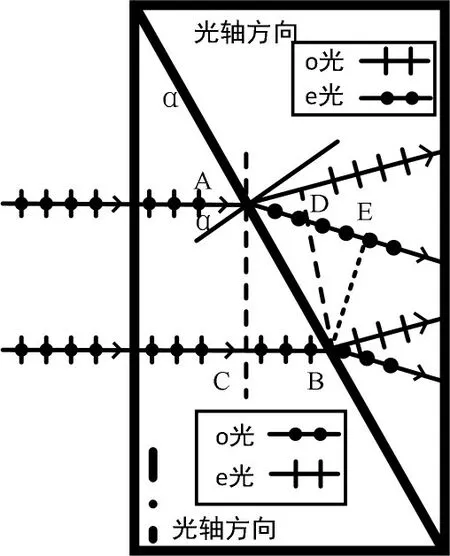
图7 第二块三棱镜中偏振光的整体传播

4 光从渥拉斯顿棱镜出射

假设渥拉斯顿棱镜外为空气等各向同性介质，折射率为n0。一般情况下，n0＜no,ne。

4.1 p偏振光的波面、传播方向与偏振方向

在第二块三棱镜中，o 光为p 偏振线偏光，波线垂直于波面。如图8 所示，假设下光线、上光线分别与出射界面交汇于B'点和F 点，过B’作BD 的平行线，交上光线与D'。B'D'亦为o 光的波面。当下光线到达界面B'点时，上光线需传播的几何长度才能到达界面。根据假设，渥拉斯顿棱镜外光传播速度快且各向同性，故以B'点为次波源中心的球面次波半径大于，过F 点作此半球面的切线，设切点为G。连接B'和G，并延长，即得到下光线的出射方向，过F 作B'G 的平行线，即得到出射的上光线。

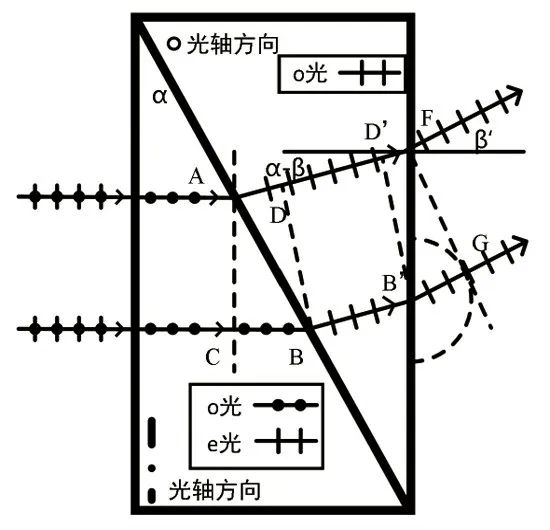
图8 从渥拉斯顿棱镜出射的p偏振光

考虑到p 偏振为本征偏振态，出射的光线仍为p 偏振光。但由于最终出射光已经是在各向同性纸介质中，不再有o 光和e 光说法。根据作图过程，有：

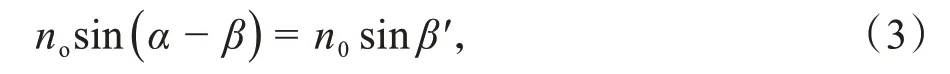
其中α-β为此次折射的入射角，n0为棱镜外介质折射率，β'为出射角。由于no＞n0,光线进一步向上走离。

4.2 s偏振光的波面、传播方向与偏振方向

在第二块三棱镜中，s 线偏光为e 光，波线垂直于波面。如图9 所示，假设上光线、下光线分别与出射界面交汇于E'点和H 点，过E'作EB 的平行线，交下光线与B'。E'B'亦为e 光的波面。当上光线到达界面E'点时，下光线需传播的几何长度才能到达界面。根据假设，渥拉斯顿棱镜外光传播速度快且各向同性，故以E'点为次波源中心的球面次波半径大于，过H 点作此半球面的切线，设切点为I。连接E'和I，并延长，即得到上光线的出射方向，过H 作E'I 的平行线，即得到出射的下光线。考虑到s 偏振为本征偏振态，出射的光线仍为s 偏振光。但由于最终出射光已经是在各向同性纸介质中，同理不再有o 光和e 光说法。根据作图过程，有：

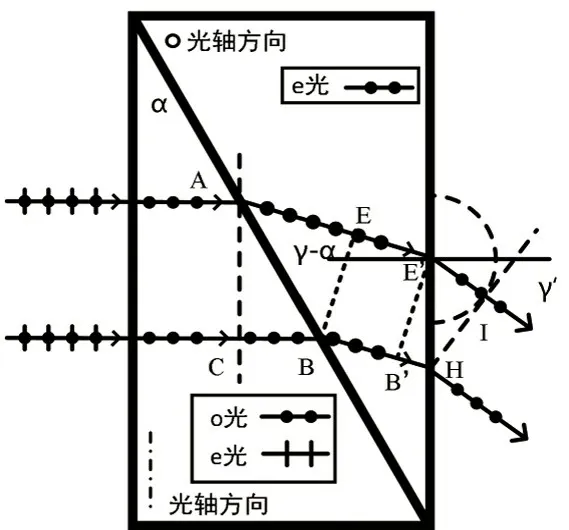
图9 从渥拉斯顿棱镜出射的s偏振光

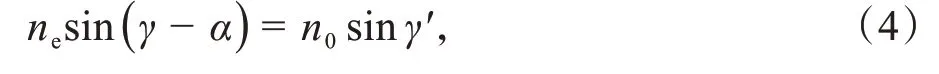
其中γ-α为入射角，γ'为出射角。由于ne＞n0,光线进一步向下走离。

根据式（1）～（4），可以计算出最终出射的s 偏振光和p偏振光的分离角：

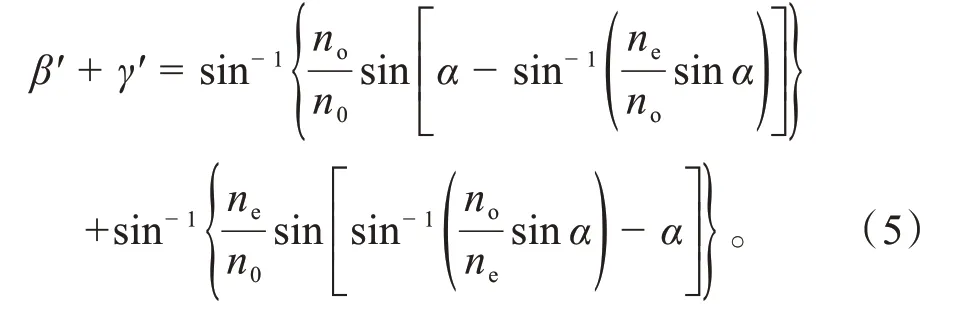
由式5 可知，当光线垂直入射到渥拉斯顿棱镜时，在已知棱镜顶角α、o光折射率no、e光折射率ne及渥拉斯顿棱镜外介质折射率n0等参数前提下，最终分离角可以唯一确定。

5 小结

通过惠更斯作图法，以负晶体为例，详细阐明偏振光在渥拉斯顿棱镜中的传播过程，分析了偏振光的走离机制和原因，特别是光线从第一块三棱镜入射到第二块三棱镜o光变e光，e光变o光的过程，得到了光线的最终出射角与棱镜顶角α、o光折射率no、e光折射率ne等参数的定量计算关系式。相关过程和结果可为正在从事相关思考的师生、科研人员提供一定参考。