模糊拟度量空间中的一种序关系及其在最优化问题中的应用
2023-01-13吴健荣
唐 肖,吴健荣
(苏州科技大学 数学科学学院,江苏 苏州 215009)
Menger[1]首次提出概率度量空间的定义,利用分布函数来刻画空间中两点间的距离。然而,许多情况下,测量两点间距离的不确定性不一定是由随机性引起的。1975年,Kramosil等[2]将两点之间的距离表示成一个模糊集,提出了模糊度量的概念,并以此建立了模糊度量空间(通常被称为KM模糊度量空间)的基本框架。1994年,George等[3]改进了模糊度量并以此建立了GV模糊度量空间。
2004年,Gregori等[4]去掉了GV模糊度量定义中的对称性,提出了模糊拟度量的概念,并且证明了每一个拟度量都可以诱导生成一个模糊拟度量,每一个模糊拟度量空间都可以拟度量化。2005年,Gregori等[5]利用柯西序列研究了模糊拟度量空间的完备性和完备化问题。随后,他们研究了模糊拟度量空间的双完备化问题[6],给出了可双完备化的充要条件。2010年,Rodriguez-Lopez等[7]研究了Hausdorff模糊拟度量的性质及应用。2011年,Castro-Company等[8]在双拓扑空间框架下,证明了每个模糊拟度量空间在等距同构意义下都有唯一的双完备化空间。随后文献[9]研究了预序完备的模糊拟度量空间上一类广义压缩的不动点定理以及在算法中的应用。2018年,Sánchez等[10]进一步研究了模糊拟伪度量的代数结构。在拟度量空间中,可以自然地诱导出一个偏序关系[11]。但在模糊拟度量空间中,相应的问题还没有得到有效开展。受此启发,本文在模糊拟度量空间中引入一种偏序关系,对其性质进行比较深入的研究,并以此为工具,讨论模糊拟度量空间上的优化问题。
1 预备知识
本文中,X是一非空集合,∅表示空集,N表示自然数集。
定义1[12]称二元算子*:[0,1]×[0,1]→[0,1]为连续t-模,如果:
1)*满足结合律和交换律;
2)*是连续的;
3)a*1=a,∀a∈[0,1];
4)当a≤c且b≤d(a,b,c,d∈[0,1])时,a*b≤c*d。
引理1[13]设算子*:[0,1]×[0,1]→[0,1]是连续t-模,
1)若r1>r2,则存在r3∈(0,1),使得r1*r3>r2,其中r1,r2∈(0,1);
2)若r4∈(0,1),则存在r5∈(r4,1),使得r5*r5>r4。
定义2[3]设X是一非空集合,*是连续t-模,如果映射M:X2×(0,∞)→(0,1]满足以下条件:∀x,y,z∈X,
MQ1)∀t>0,M(x,x,t)=1;
MQ2)∀t>0,M(x,y,t)=M(y,x,t)=1⟹x=y;
MQ3)∀s,t>0,M(x,y,t)*M(y,z,s)≤M(x,z,t+s);
MQ4)M(x,y,·):(0,∞)→(0,1]是连续的;
则称(M,*)为X上的一个GV模糊拟度量,称(X,M,*)为GV模糊拟度量空间。
以下除非特别指明,所称模糊拟度量(空间)均指GV模糊拟度量(空间)。
若模糊拟度量M满足对称性,即∀x,y∈X,∀t>0,都有M(x,y,t)=M(y,x,t),则称其为模糊度量,称(X,M,*)为模糊度量空间。
引理2[3]∀x,y∈X,M(x,y,·)是递增的。
定义3[3]设(X,M,*)是一个模糊拟度量空间,x∈X,r∈(0,1),t>0,分别称
BM(x,r,t)={y∈X|M(x,y,t)>1-r},
(1)
BM[x,r,t]={y∈Y|M(x,y,t)≥1-r}
(2)
为X的以x为中心、r为半径的开球和闭球。
设A⊆X,若∀x∈A,都存在t>0和r∈(0,1),使得BM(x,r,t)⊆A,则称A是开集。Gregori等[4]指出,(X,M,*)上开集的全体构成X上一个拓扑,称其为由模糊拟度量M诱导的拓扑,记为τM。

对于模糊拟度量空间(X,M,*),令M-1(x,y,t)=M(y,x,t),x,y∈X,显然M-1也是模糊拟度量;令Ms(x,y,t)=min{M(x,y,t),M-1(x,y,t)},x,y∈X,则Ms是模糊度量,由Ms导出的拓扑记为τMs。
X中的子集A关于拓扑τM和τM-1的闭包分别记为cMA和cM-A。
定理1设(X,M,*)为模糊拟度量空间,则
1)拓扑τM是T0分离的;
2)拓扑τM是T1分离的充要条件是M满足
∀t>0,M(x,y,t)=1⟹x=y;
(3)
3)当M是模糊度量时,拓扑τM是T2分离的。
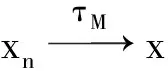
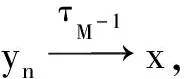
证明1)设x,y∈X,且x≠y。由MQ2)知,∃t0>0,使得0 2)先证充分性。设x,y∈X,且x≠y。由(3)式知,∃t1,t2>0,使得0 再证必要性。用反证法,假设τM是T1分离的,且∀t>0,M(x,y,t)=1,但x≠y。由于τM是T1分离的,所以{y}关于τM是闭集,于是存在x的开邻域BM(x,r0,t0),使得BM(x,r0,t0)∩{y}=∅,即y∉BM(x,r0,t0),亦即M(x,y,t0)≤1-r0,这与M(x,y,t)=1(∀t>0)矛盾。 3)设x,y∈X,且x≠y,由MQ2)知,∃t0>0,使得 0 (4) 由引理1,∃(1-r0)*(1-r0)>m0。而BM(x,r0,t0/2)、BM(y,r0,t0/2)分别为x、y的开邻域,但 BM(x,r0,t0/2)∩BM(y,r0,t0/2)=∅。 (5) 事实上,若∃z∈BM(x,r0,t0/2)∩BM(y,r0,t0/2),则M(x,z,t0/2)>1-r0,M(y,z,t0/2)>1-r0,从而 M(x,y,t0)≥M(x,z,t0/2)*M(y,z,t0/2)≥ (1-r0)*(1-r0)>m0, 这与(4)式矛盾,所以(5)式成立。由此可见,拓扑τM是T2分离的。证毕。 注1满足条件3)的模糊拟度量空间,称为T1模糊拟度量空间。 文献[9]在KM模糊拟度量空间中引入了一种序关系,但对其性质没有作讨论。类似地,本文在(GV)模糊拟度量空间中引入对应的序关系。 定义4设(X,M,*)是模糊拟度量空间,在其上定义一个关系“≤”如下: x≤y当且仅当∀t>0,都有 M(x,y,t)=1。 (6) 根据定义4容易得到以下结论。 定理2设(X,M,*)是模糊拟度量空间,则 1)“≤”满足自反性、传递性和反对称性,即“≤”是X上的一个偏序; 2)“≤”为相等关系当且仅当(X,M,*)为T1分离的模糊拟度量空间。 ∀y∈X,令 K(y)={x∈X:x≤y}, (7) 即x∈K(y)当且仅当x≤y。 定理3设(X,M,*)是模糊拟度量空间,y∈Y,则K(y)=cM{y},从而K(y)关于拓扑τM是闭集。 M(x,y,t)≥M(x,xn,t/2)*M(xn,y,t/2)→1(n→∞), 于是x∈K(y)。所以K(y)关于τM是闭集,由此可知cM{y}⊆K(y)。 反之,设x∈K(y),则∀t>0,有M(x,y,t)=1。于是,对x的任意一个邻域BM(x,1/n,1/n),总有y∈BM(x,1/n,1/n),即{y}∩BM(x,1/n,1/n)≠∅,于是x∈cM{y}。由x的任意性得到K(y)⊆cM{y},从而K(y)=cM{y}。证毕。 设A为模糊拟度量空间(X,M,*)中的子集,记 ↑A={y∈X:∃x∈A,x≤y}, ↓A={y∈X:∃x∈A,y≤x}。 定理4设A为模糊拟度量空间(X,M,*)中的子集。 1)若A关于拓扑τM为开集,则A为上闭集,即↑A=A; 2)若A关于拓扑τM为闭集,则A为下闭集,即↓A=A。 证明1)任取y∈↑A,则∃x∈A,使得x≤y。若A为开集,则存在x的开邻域BM(x,r0,t0),使得BM(x,r0,t0)⊆A。由于x≤y,所以M(x,y,t0)=1,从而y∈BM(x,r0,t0)⊆A。由y的任意性知↑A⊆A,于是↑A=A。 2)任取y∈↓A,则∃x∈A,使得y∈↓{x}。由定理2,y∈cM{x}⊆cMA。若A为闭集,则y∈A。由y的任意性知↓A⊆A,于是↓A=A。证毕。 定理5设A为模糊拟度量空间(X,M,*)中的子集,则 ↑A=∩{B∈τM:A⊆B}。 证明显然“↑”为单调增的集值算子,因此由定理4的1)可得 ↑A⊆∩{B∈τM:A⊆B}。 任取y∉↑A,则∀x∈A,都有xy,从而存在tx>0,使得0 ∩{B∈τM:A⊆B}⊆↑A。 综上所述,↑A=∩{B∈τM:A⊆B}。证毕。 M(x,y,t)≥M(x,xn,t/2)*M(xn,y,t/2)→1(n→∞)。 所以M(x,y,t)=1。从而x≤y。证毕。 证明∀t>0,由xn≤zn≤yn得∀n∈N,M(zn,yn,t/2)=1,M(xn,zn,t/2)=1。 M-1(zn,x,t)≥M(x,xn,t/2)*M(xn,zn,t/2)= M(x,xn,t/2), M(zn,x,t)≥M(zn,yn,t/2)*M(yn,x,t/2)=M(yn,x,t/2), 定理8设(X,M,*)是模糊拟度量空间,x,y∈X。若x≤y,则∀t>0,∀z∈X,总有M(x,z,t)≥M(y,z,t)。 证明∀t>0,由x≤y得到M(x,y,t)=1,所以∀s>t,总有 M(x,z,s)≥M(x,y,s-t)*M(y,z,t)= M(y,z,t)。 由于映射M(x,y,·)连续,从而M(x,z,t)≥M(y,z,t)。证毕。 先利用上节引入的序关系,给出模糊拟度量空间上集合的极小点和极大点的概念。 定义5设(X,M,*)是模糊拟度量空间,A⊆X。令 minA={a∈A:A∩K(a)={a}}, (8) maxA={a∈A:A∩K-1(a)={a}}, (9) 其中K-1(a)={x∈X:M(a,x,t)=1,∀t>0},则分别称minA和maxA中的点为A的极小点和极大点。 定理9设(X,M,*)是模糊拟度量空间,A⊆X。a∈minA当且仅当 1)a∈A, 2)如果y∈A且y≤a,则y=a。 证明必要性。假定A⊆X,a∈minA。由(8)式得到a∈A且A∩K(a)={a}。如果y∈A且y≤a,则y∈A∩K(a),故y∈{a},即y=a。 充分性。由条件1)知a∈A,从而A∩K(a)⊇{a}。由条件2)知,A∩K(a)⊆{a}。由minA的定义知,a∈minA。证毕。 设X是一个非空集合,(Y,M,*)、(Z,M′,*′)是模糊拟度量空间。考虑如下带约束条件的最优化问题: minf(x),g(x)≤a,x∈P。 (10) 其中:f:X→Y;g:X→Z;a∈Z;P⊆X。 令C=P∩{x∈X:g(x)≤a},则上述问题(10)的解集即为minf(C)。由于向量最优化问题、向量集值最优化问题均可用模糊拟度量空间中最优化问题来表述,所以问题(10)具有很大的一般性。 定义6设(X,M,*)是一个模糊拟度量空间,A⊆X,分别称infA=min(cM-A)和supA=max(cMA)为A的下确界和上确界。 注2上述上、下确界概念不同于由偏序“≤”导出的上、下确界概念。 定义7设f:X→Y是拓扑空间X到模糊拟度量空间(Y,M,*)的映射,D(f)是f的定义域,x0∈D(f)⊆X。 1)如果∀t>0, 则称f在x0处上半连续; 2)如果∀t>0, 则称f在x0处下半连续。 若f在集合C的任意一点处上半(下半)连续,则称f在集合C上是上半(下半)连续的。 定理10设X是一个拓扑空间,C是X中的紧子集,(Y,M,*)是模糊拟度量空间,f:C→Y是上半连续映射。如果f在C上存在下确界,则 1)该下确界是可达的,即对于a∈inff(C),存在x′使得f(x′)=a; 2)minf(C)≠∅。 证明1)由假设,存在a∈inff(C)=min(cM-f(C)),于是 (cM-f(C))∩K(a)={a}。 (11) 及 f(x′)∈f(C)⊆cM-f(C)。 (12) M(f(x′),a,t)≥M(f(x′),f(xni),t/2)* M(f(xni),a,t/2)→1。 于是,M(f(x′),a,t)=1,即f(x′)∈K(a)。结合(11)、(12)式,可得f(x′)=a,这表明f在C上的下确界是可达的。 2)由上述证明过程可知,{a}=f(C)∩K(a),从而f(x′)=a∈minf(C),于是minf(C)≠∅。证毕。 类似地,可以得到以下定理。 定理11设X是一个拓扑空间,C是X中的紧子集,(Y,M,*)是模糊拟度量空间,f:C→X是下半连续映射。如果f在C上存在上确界,则 1)该上确界是可达的; 2)maxf(C)≠∅。2 模糊拟度量空间中的序关系

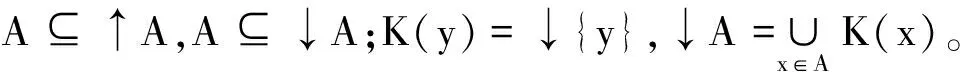





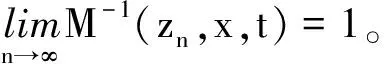

3 序关系在最优化中的应用


