基于FCM聚类的模糊综合评价方法
2023-01-13赵春兰
何 婷,赵春兰,2*,李 屹,王 兵
(1 西南石油大学 理学院,四川 成都 610500;2 西南石油大学 人工智能学院,四川 成都 610500;3 西南石油大学 计算机科学学院,四川 成都 610500)
综合评价是指对事物的多层次、多属性、多方位进行分析评价的过程。基于模糊理论的评价方法能够有效地处理指标因素的模糊性和随机性,近年来在实践中得到越来越多的关注和应用[1]。模糊综合方法(fuzzy comprehension evaluation,FCE)可以综合考虑各影响因素的特点,构造隶属度函数,确定各指标的隶属度,从而得出最终的重要程度排序。这种排序过程是将一些界限不清或定义模糊的指标进行量化,通过模糊函数将那些难以量化的指标转化为量化指标,使评价过程更加合理、准确[2-3]。
模糊综合评价的核心问题包括评价指标权重的确定、隶属函数的构造和综合算子的选择。大部分学者将重点放在如何改进权重计算和合成算子上,对隶属函数的研究相对较少。目前,隶属函数一般根据经验确定[1,4-5],主要有模糊统计、二元对比排序和模糊分布等方法,其中模糊分布最为常见,主要包括矩形分布、梯形分布、K次抛物型或半抛物型分布、高斯分布和柯西分布。但是,上述根据模糊分布确定隶属度的过程难免会受到主观性的较大影响,导致评价结果出现偏差。同时,文献[5]指出隶属函数作为模糊集合论的基础,用精确的函数曲线来处理模糊现象,精确地解决模糊问题,违反了模糊集合论的基本原理。因此,云模型和灰色关联分析法中的灰关联系数[4,6-7]被应用到隶属度矩阵确定过程。在确定隶属度函数后,需根据评价指标的评价标准进行计算得到隶属度值,然而实际生活中部分被评价对象不存在评价指标的等级划分标准,评价时大多是根据经验或行业标准划分指标阈值,缺乏科学的理论依据[6]。因此,现阶段综合评价的主要问题是建立科学的指标分级体系和客观的隶属度矩阵。而模糊聚类算法作为一种理论成熟、应用广泛的无监督聚类学习算法,可以通过无监督学习确定元素属于各个聚类簇的隶属程度,对每一聚类簇进行模糊识别实现数值与模糊语言之间的转换。因此,将模糊C均值聚类(fuzzyC-means,FCM)算法应用到指标阈值和隶属度矩阵的确定过程中,提出一种基于FCM模型的模糊综合评价方法,以解决评估过程中的主观性、模糊性和随机性问题。因为在实际生活中,部分被评价对象的指标具有评价标准,所以本文将分为是否存在评价指标标准两种情况对FCM算法进行研究:当存在指标标准时,根据评价标准确定最佳聚类中心,代入FCM中确定隶属度矩阵;不存在指标标准时,通过AP聚类确定模糊均值聚类的初始聚类中心,改善算法对聚类中心初值选取的随机性及对样本的敏感性,从而减小陷入局部最优解的可能性,根据聚类结果建立合理的指标分级体系和隶属度矩阵。
1 模糊聚类理论
聚类分析是进行分组处理和数据划分的有效方法,模糊聚类方法考虑样本间的相互关系,分析它们之间相互的隶属度,对类与类之间有交叉的数据集进行聚类[8]。模糊C均值(FCM)聚类在分类评价领域已有大量研究成果。FCM聚类分析方法可以定性且定量地确定研究对象间的“亲疏关系”,并能够在分类对象没有预先给定标识的情况下,依据对象间的相似程度,自动将其划分为有意义的类别[9]。
1.1 模糊C均值聚类(FCM)
FCM是用隶属度确定每个数据点属于某个聚类程度的一种聚类算法,把n个对象分为C组,并求每组的聚类中心,用隶属度uki∈[0,1]来确定其属于各个类别的程度,uki满足
(1)
其中:uki表示第i个样本属于第k类的隶属度。FCM算法是寻找使目标函数J达到极小值时的隶属度矩阵U和聚类中心c。目标函数表达式为
(2)

利用拉格朗日乘子法求解(2)式,可得聚类中心ν和隶属度u的迭代公式如下:
(3)
(4)
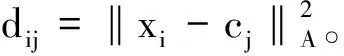
1.2 基于AP聚类改进的FCM聚类算法
FCM 算法需要依据先验知识指定聚类类别数,算法的灵活性受到限制,并且聚类结果对聚类中心的初值十分敏感,依赖性较大。初始聚类中心选择不当将会导致聚类结果陷入局部极值点,得不到全局最优解[10]。因此,文中将近邻传播(AP)聚类算法用于FCM聚类,对初始聚类中心选取进行优化。AP聚类算法[11-13]的优点为无需事先指定聚类个数和初始聚类中心,可以通过传递数据点的信息找到最佳聚类中心。由此,本文提出将模糊均值聚类算法与AP聚类算法相结合的改进方案,根据AP聚类算法确定FCM聚类算法的初始聚类中心,改善聚类中心初值选取的随机性及敏感性,降低陷入局部最优解的可能性。
1.2.1 AP聚类
AP聚类[12]的基本思想是将全部数据看作网络节点,将所有节点视为潜在聚类中心,通过计算节点间的相似度,构成相似度矩阵,再通过节点间的消息传递,找到最合适的聚类中心。节点间传递的消息分为吸引度和归属度。吸引度γ(i,k)反映k点适合作为i点的聚类中心的吸引程度;归属度a(i,k)反映i点选择k点作为其聚类中心的归属程度。AP聚类分为 4个步骤。
步骤1初始化吸引度和归属度矩阵为0矩阵,并计算相似度矩阵s,确定参考度p。
步骤2计算吸引度和归属度,即
(5)
(6)
步骤3更新吸引度和归属度。为了使算法在迭代过程中避免震荡,在每次迭代更新时加入阻尼系数λ(λ∈(0,1))调节算法收敛速度,更新公式如下:
γt+1(i,k)=λγt(i,k)+(1-λ)γt+1(i,k),
(7)
at+1(i,k)=λat(i,k)+(1-λ)at+1(i,k)。
(8)
步骤4迭代执行步骤2和3,更新γ(i,k),利用迭代后的γ更新a(i,k);然后得到H个聚类中心点,并据此划分出H个聚类,AP聚类结果如图1所示。

图1 AP聚类结果示意图
1.2.2 基于AP聚类改进的FCM聚类算法过程
将AP聚类计算出的聚类中心作为FCM聚类的初始聚类中心,排除因随机选择初始聚类点而对聚类结果造成的影响,进而保证改进得到的聚类中心为全局的最优解,其具体算法步骤如下。
步骤1设定聚类参数,其中包括参考度p、模糊指数权重m、最小误差e,以及最大迭代次数。
步骤2通过AP聚类确定c个初始聚类中心。
步骤3利用公式(2)和(4)计算目标函数和初始隶属度矩阵。
步骤4判断是否停止迭代。如果‖J(k+1)-J(k)‖ 步骤5令k=k+1,根据(3)式和(4)式更新聚类中心和隶属度矩阵,返回步骤4。 因子集是由影响被评价对象的各指标因子组成的集合,用X表示: X={x1,x2,…,xm}。 评价集是评价者对被评价对象做出各种总体评价结果的集合,用V表示: V={v1,v2,…,vn}。 从单因素评价出发,确定被评价对象对评价集的隶属程度,称为单因素模糊评价,进而得到由被评价对象的所有指标评价结果组成的模糊关系矩阵U。现实生活中,部分被评价对象存在一定的评判标准,比如地下水质量,依据我国《地表水环境质量标准GB/T14848-93》将地下水质量划分为5类。所以将改进的FCM算法引入评价模型时,需根据指标阈值是否存在进行分类研究。 2.3.1 存在指标阈值:隶属函数的建立 当被评价对象存在评判标准时,无需确定指标阈值,只需确定隶属度值。对此类被评价对象进行分析,发现该评价对象的各个指标存在相应的等级划分区间,故可将每一等级区间视为一类,那么可以认为每一区间中心对应着每一类的最佳聚类中心。所以,利用FCM算法确定此类情况的隶属度矩阵时,其目的不再是寻找使目标函数J达到极小值时的隶属度矩阵U和聚类中心c,而是在给定最佳聚类中心的前提下,寻找使目标函数J达到极小值时的隶属度矩阵U,将二参数优化问题修正为单参数的条件极值问题,目标函数为 (9) 其中,dij表示第i个样本与第j个聚类中心的欧式距离,可根据指标数据与评判标准计算。同样地,利用拉格朗日乘子法求解(9)式,得到隶属度函数 (10) 显然,当数据点与某一聚类中心距离越接近时,表示该数据点与包含此聚类中心的数据集更相似,那么该数据点隶属于此数据集的可能性就越大,其对应的隶属度值就越高。如图2中数据点x1,其中d11 图2 隶属度示意图 2.3.2 不存在指标阈值:指标阈值和隶属度矩阵的建立 现实生活中,虽然部分被评价对象存在统一的评判标准,但大部分被评价对象并不存在等级划分标准值。故利用模糊分布法确定隶属度函数时,还需人为确定评价等级的阈值,导致评价结果过于主观。FCM聚类算法通过模糊划分将数据自动聚类,最后得到最佳聚类中心和隶属度矩阵。利用每一等级区间为一类的思想,根据改进FCM聚类算法的聚类结果客观确定指标阈值。 根据聚类结果建立等级划分阈值,具体过程如下。 步骤1利用AP聚类算法确定聚类个数c,即通过AP聚类算法得到初始聚类中心Ck(k=1,2,…,c)。 步骤2利用由AP聚类算法得到的初始聚类中心进行FCM聚类,得到最佳聚类中心V={v1,v2,…,vc}(排序后)和隶属度矩阵U。 步骤3根据隶属度矩阵得到所有数据点的聚类结果,计算每类的上下限值si和fi。 步骤4将聚类结果进行适当划分,得到分级界限值。将某一聚类上限si与相邻聚类下限fi+1的中间值ti作为边界值,划分子区间。结合实际情况,对分割好的区间进行相应的语义解释A1,A2,…,Ac,则各区间端点值ti即是分级界限值。如图3所示。 图3 指标阈值划分结果 对权重向量A和模糊关系矩阵R进行模糊合成运算,得到综合评判指标B: B=A*R。 “*”的取法不同,评价结果也不完全相同。在实际应用时,应根据不同的目的选择恰当的运算模型。模糊综合评判的结果是被评价对象对各评价集的综合隶属度,反映了所有因素的综合影响。确定评判对象具体结果常用的原则是最大隶属度原则,但该原则会造成一定的信息损失,导致评判结果区分度低,不能真实反映研究对象间的差异[14]。所以,本次评价采用加权平均原则对结果矩阵进行处理,即 (11) 其中,k为待定系数(k=1或2),目的是控制较大的bj所引起的作用。当k趋于无穷大时,加权平均原则就是最大隶属度原则[5],新模型的流程见图4。 图4 基于改进FCM算法的评价模型流程图 利用四川某流域36个监测断面的化学需氧量、生化需氧量、高锰酸盐指数、氨氮、总磷和溶解氧这6项指标数据来验证新方法的有效性和可行性。选取各个监测面2011—2015年监测数据的年均值数据进行分析评价,如表1所示。 表1 各断面水质指标实测值 本文采用变异系数法[7,15]来计算指标权重。变异系数法是直接利用各项指标所包含信息计算权重的一种客观赋权法,通过计算得到指标权重集:A=[0.474 9,0.116 5,0.180 8,0.084 9,0.027 7,0.115 3]。为将新模型的评价结果与传统的模糊综合评价模型(选择将半梯形函数作为隶属函数)结果进行对比,设置各指标权重值不变。 为验证新模型的有效性,本文讨论水质指标阈值是否存在两种情况:当水质指标阈值已知时,依据《地表水环境质量标准》,水质类别可分为Ⅰ类、Ⅱ类、Ⅲ类、Ⅳ类和Ⅴ类水体,故最终确定FCM算法的聚类个数为5;当水质指标阈值未知时,将指标数据带入AP聚类中,得到FCM的聚类数以及初始聚类中心,再引入FCM模型中,计算各指标的隶属度矩阵,得到所有监测断面的模糊关系矩阵并计算指标阈值建立指标评价体系,如表2所示。然后,根据权重向量和隶属度矩阵进行模糊运算,得到所有断面的水质综合评判指标,最后采用加权平均原则对结果矩阵进行处理,得到最终评价结果。两种情况的各断面等级与排名结果见表3。 表2 水质指标评价体系 表3 四川某水域所有监测断面的两类方法综合评价等级与排名 将2类评价结果与传统的模糊综合评价方法和单因子评价结果进行对比,根据图5和6,4种模型评价趋势基本一致且2类新方法与单因子评价结果的相关系数均在0.7以上,与传统模糊综合评价结果相关系数均在0.85以上,评价结果具有一定的一致性。同时发现2种新模型的评价结果处于传统模糊综合评价方法和单因子评价结果之间,表明新模型可以避免单因子评价模型仅强调最差单项指标导致评价结果较为片面以及传统模糊综合评价中人为选择隶属度函数导致结果主观性较强的问题。 图5 4种模型综合评价等级对比图 图6 4种模型评价等级结果的相关系数热力图 再对传统评价模型与2类新模型的评价结果排名进行分析(见图7),发现2类新模型的排名结果趋势大体一致,而传统评价模型与2类新模型排名结果差异较大,所以对排名差异较大的监测面进行分析。以M和N断面为例,评价结果如表4,传统评价模型认为M断面水质优于N断面,而两类新模型结果相反。分析两断面的指标数据(见表5),可以发现除高锰酸盐指数和总磷指标外,其余指标无明显差别,且高锰酸盐指数均处于地表水环境质量标准的Ⅲ类以下,但是M断面的总磷指标值是N断面总磷指标值的7.6倍,M断面的污染程度应是比N断面严重,可见2类新模型的结果更为合理。 表4 M和N断面的3种模型评价结果 表5 M和N断面的指标数据 图7 3种模型的评价结果排名对比 本文提出一种利用改进的FCM模型优化传统模糊综合评价的新方法,引入模糊聚类的思想解决现阶段综合评价系统中部分指标阈值未知的问题,同时用FCM模型代替评价过程中的精确函数曲线,解决隶属度确定过程的主观性问题和模糊性问题。 本文针对实际生活中评价指标是否存在标准阈值进行分类讨论:1)当被评价对象存在评价标准时,将FCM模型简化为单纯的条件极值问题,根据评价指标等级划分区间计算出最佳聚类中心,在给定最佳聚类中心的条件下,求解目标函数,得到对应的隶属度矩阵;2)当被评价对象不存在评价标准时,不能运用精确函数计算隶属度矩阵,本文首先利用AP聚类算法得到初始聚类中心,降低FCM聚类结果对初始聚类中心的依赖;再通过改进的FCM模型对数据进行模糊划分,客观确定隶属度矩阵,并且根据得到的聚类结果建立一套评判标准。 将指标数据通过改进后的FCM模型进行划分,对其进行分级,得到等级阈值,使得分级更加科学。同时,精确隶属函数计算过程繁琐,易出现误差且耗时长,而使用改进后的FCM模型计算隶属度矩阵时计算过程简单,不易出现误差且耗时短。不过对于综合评价问题,评价结果大多是相对的。因此在解决实际问题时,人们应结合问题背景知识多层次、多角度建立评价模型。2 基于改进FCM算法的评价过程
2.1 因子集和评价集的确定
2.2 权重向量的确定
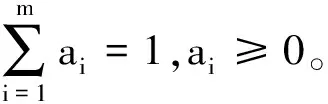
2.3 指标等级阈值和模糊评判矩阵的确定


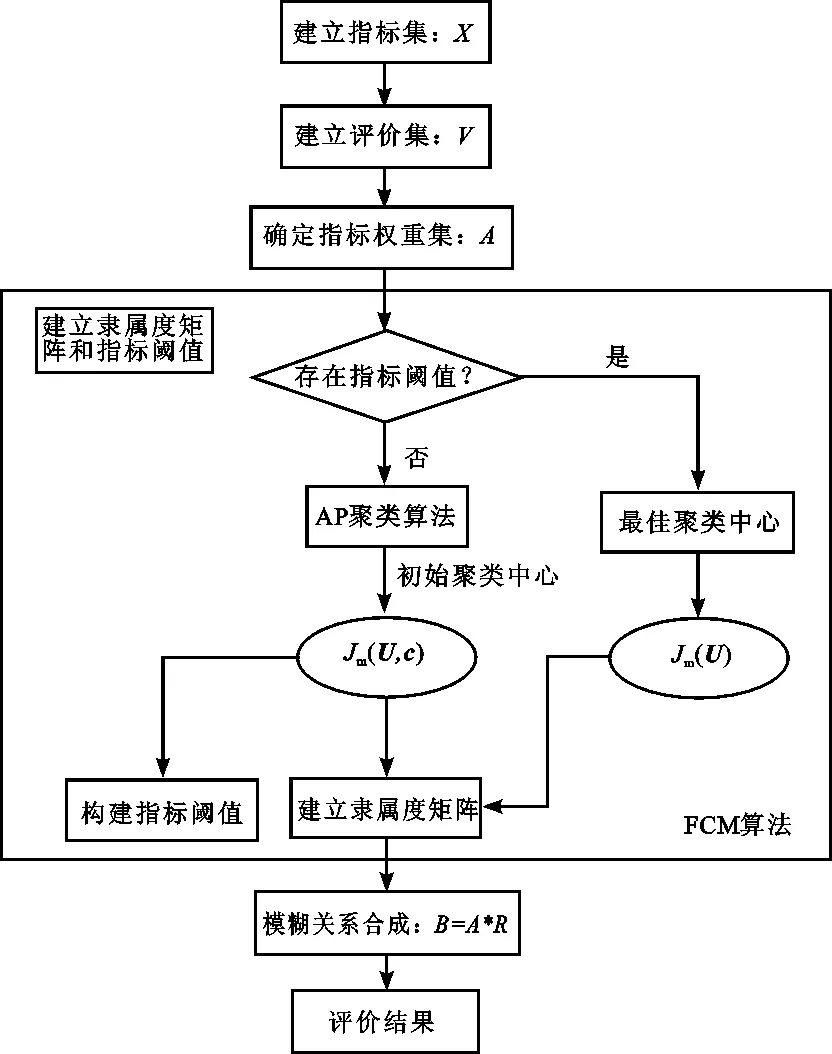
2.4 模糊综合评判
3 案例应用与结果分析
3.1 实例研究


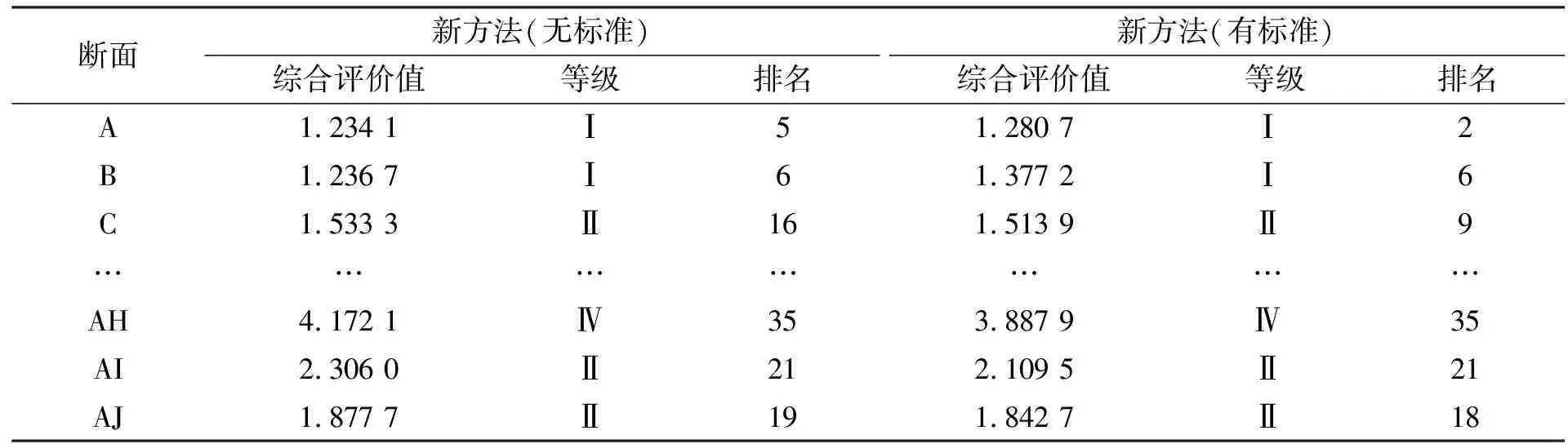
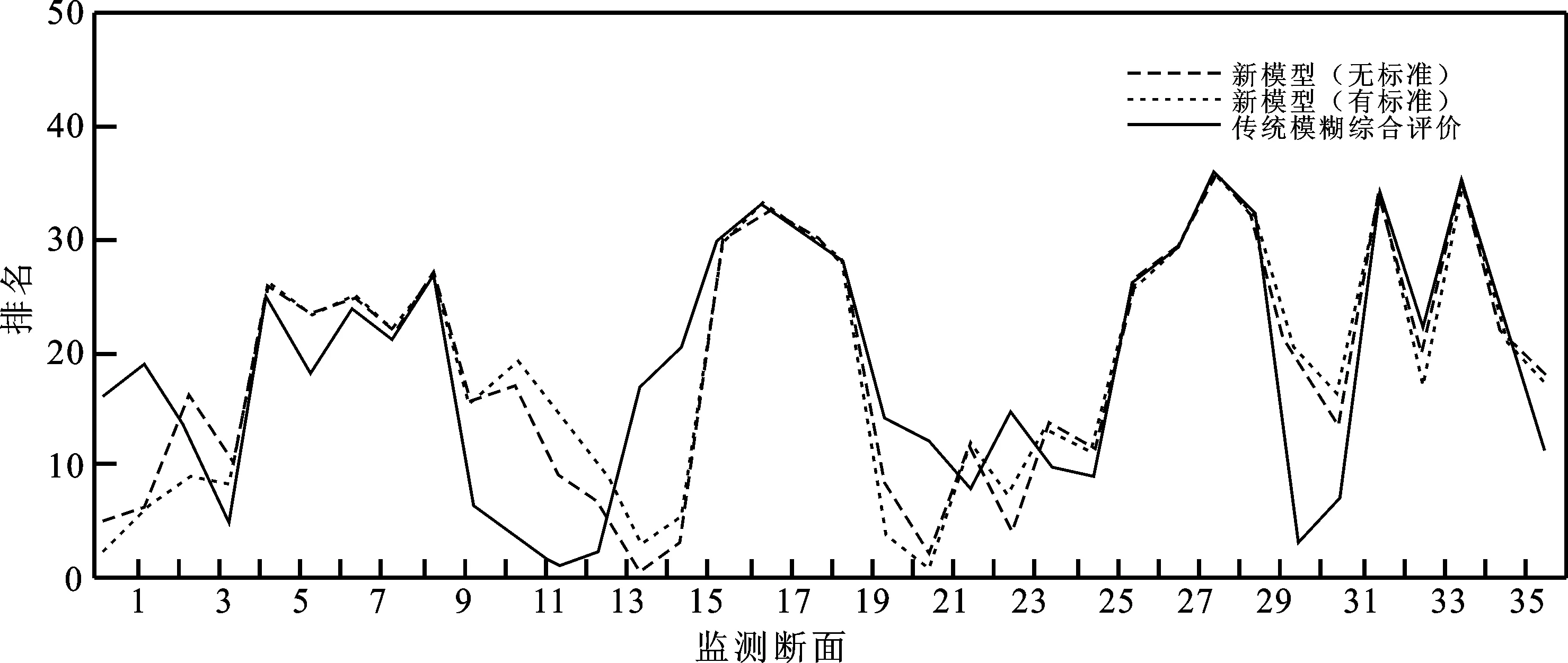
3.2 结果分析




4 结论
