开裂式阻力方向舵流固耦合机理分析
2023-01-12李永昌戴玉婷杨超
李永昌, 戴玉婷, 杨超
(北京航空航天大学 航空科学与工程学院, 北京 100191)
开裂式阻力方向舵(简称阻力舵)是目前飞翼式飞机的主要航向操纵装置之一[1-3]。 飞翼式飞机在飞行时,阻力舵会对局部流动造成较大的扰动,与升力、俯仰力矩及滚转力矩耦合较大且变化规律复杂。 大开裂角状态下的流场类似于大迎角的流场绕流,可能会引起气流分离和涡流等复杂的流场状态[4-5],对飞机的气动特性造成很大的影响,可能会导致气动弹性问题。
针对这种特殊的操纵装置,国内外开展了不同方向的研究。 Mohamad 等[6]讨论了阻力舵对飞翼式飞机偏航运动的影响,并给出了低速状态下阻力舵的操纵效率随开裂角的变化规律。 张子军等[7]通过风洞试验的方法探究了阻力舵对飞翼式飞机气动特性的影响,试验表明,在给定的迎角和来流马赫数范围内,阻力舵的舵效基本不变,并且阻力舵可以在对升力、侧力、俯仰力矩影响较小的情况下产生较大的偏航力矩。 刘其琛等[8]对阻力舵动态打开过程的非定常气动特性进行了研究,得到了升阻力系数等数据在阻力舵打开过程中的变化趋势。 韩鹏等[9]针对二维阻力方向舵模型的气动弹性问题开展了工作,为这种特殊的气动外形建立了新的颤振计算方法。
目前的流场分解手段主要有2 种:本征正交分解(proper orthogonal decomposition,POD)方法和动力学模态分解(dynamic mode decomposition,DMD)方法。 20 世纪60 年代,Lumley[10]将POD方法应用于流体力学。 POD 方法的核心思想是通过样本数据得到一组恰当的正交基函数,使得样本数据在该正交基上的投影分量依次迅速衰减,从而可以用较少的基展开获得高维数据的近似描述,构造低维动力学模型。 DMD 方法是由Schmid 等[11-12]在Koopman 分析的基础上提出的一种低维系统分解方法,基于流场的动力学特性,对流场快照进行分解,所提取的子结构在时间、空间演化特性上相互正交,可以得到流动在时间和空间上的主要特征。 DMD 方法经过不断改进发展,近年来被广泛地应用于流动现象的机理分析,如台阶流动[13]、方腔流动[14]等。 潘翀等[15]利用DMD 方法对复杂流动的实验数据进行分析,发现DMD 方法不仅能够捕捉流场的主要特征,还可以捕捉其高频谐波。 寇家庆和张伟伟[16]对现有的DMD 方法与POD 方法进行了比较,说明了DMD方法在流场分析中的优势,并讨论了DMD 方法的研究现状及未来发展方向。 Rowley 等[17]对射流流场采用DMD 分析,得到了流场中的剪切层涡和壁涡等结构。 韩亚东和谭磊[18]应用DMD 方法获得空化流场的动力学模态,揭示了空化发展和脱落的结构特征。 Menon 和Mittal[19]对俯仰运动的翼型绕流进行DMD 分析,获得了其主要的流场模态,为流固耦合运动的DMD 分析提供了方法。
本文通过计算流体力学(computational fluid dynamics, CFD)方法得到了不同雷诺数及不同开裂角下的二维阻力舵的流场数据,并基于DMD方法对各流场进行模态分解,分析了各个模态的流动特征及频率变化。 同时,通过流固耦合方法进行了二维阻力舵模型俯仰运动的机理分析,得到了不同开裂角下流固耦合系统运动形式的变化规律。
1 计算对象及方法
本文所用计算模型如图1 所示,是一个带有阻力舵的NACA0015 翼型,弦长c约为0.3 m,阻力舵安装在翼型的3/4 弦长位置,模型在1/2 弦长位置连接有扭转弹簧。 流场来流速度为V,迎角为α,规定阻力舵的开裂角β为单片舵的偏转角度。 流场网格如图2 所示,其为AMI 网格,分为外部区域和内部区域,在进行流固耦合计算时,外部网格不动,内部网格沿着边界进行移动,从而实现模型的俯仰运动。 由于主要关注翼型附近和尾流区的流动特征,主要提取内部区域的计算数据进行DMD 分析。 翼型附近靠近壁面的第1 层网格厚度y+约为1。 流场的入口条件为速度入口,出口条件设置为压力出口,翼型表面为无滑移壁面,计算时间步长为0.000 1 s,计算时选择k-ωSST 湍流模型。
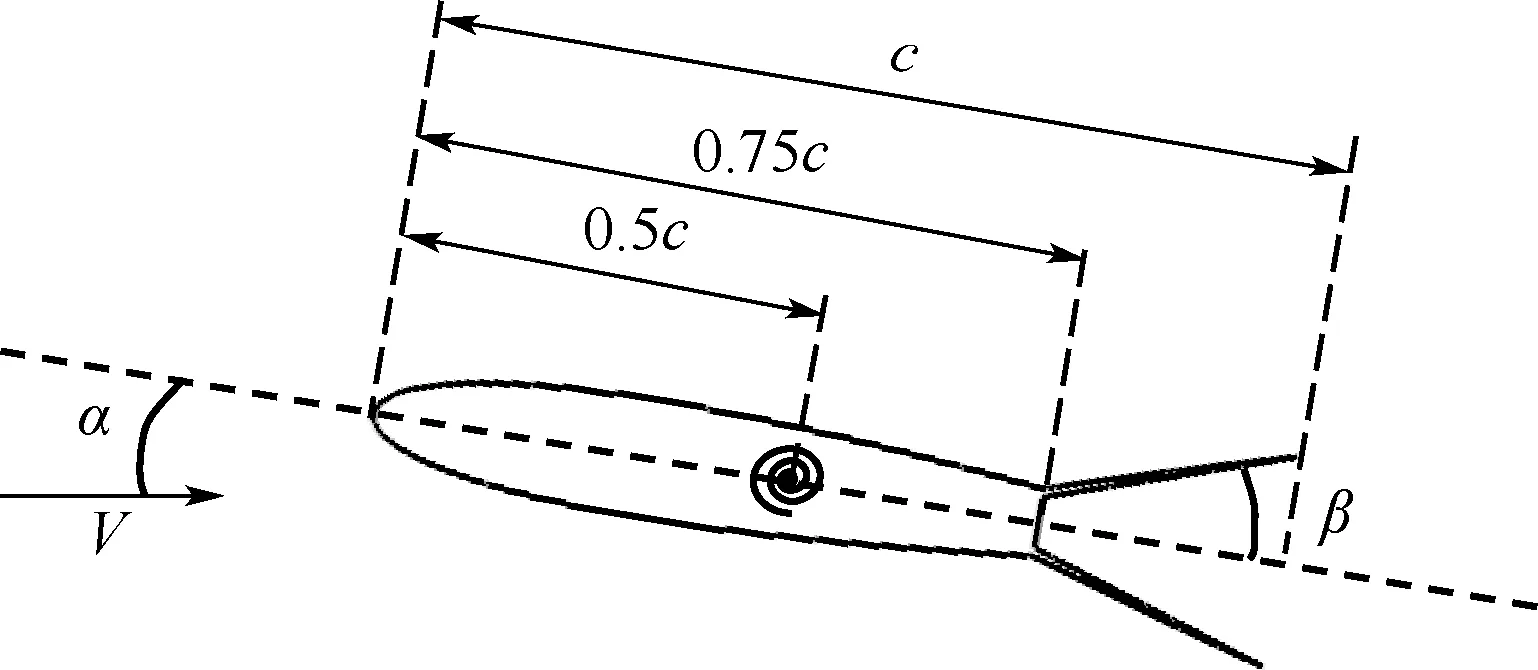
图1 阻力舵模型Fig.1 Drag rudder model
图2 流场网格Fig.2 Flow field grid
为验证数值计算方法的有效性,图3 给出了NACA0012 翼型在动态失速状态下随迎角α变化的升力系数的仿真数据与试验数据的对比。 翼型迎角α随时间t的变化规律为:α(t) =10°+15°sin (Ω t),其中,角频率Ω约为18.67 rad/s。 可以看出,本文选用的转捩SST 模型与文献中的仿真数据[20]及试验数据[21]在20°迎角的范围内相差不大。而在20°迎角以上的范围,2 组数值计算的结果与试验值均有不同程度的误差。 可以认为本文选用的SST 模型在迎角不大时的计算数据是可靠的。
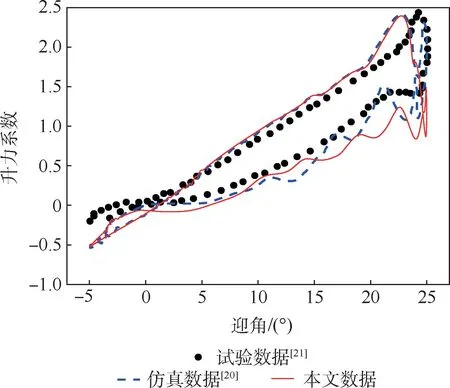
图3 不同迎角时升力系数的计算结果与试验值Fig.3 Numerical and experimental aerodynamic coefficients with different angles of attack
为了确保计算效率的同时保证计算的精度,对阻力舵的流场网格进行了网格无关性验证。 选用了3 套流场网格,其外部网格基本一致,而内部网格边界层向外的网格增长率分别为1.05、1.1、1.15。 各自的网格数量分别为15 万(细网格)、8 万(中等网格)、3 万(粗网格)。 计算选用转捩SST 模型,来流速度为10 m/s,2°迎角,时间步长为1 ×10-4s。 3 套网格在相同流场条件下计算得到的翼型表面俯仰力矩随时间变化曲线如图4 所示,力矩中心为翼型0.5 倍弦长位置。 可以看出,中等密度的网格满足计算精度。 为了保证计算精度的同时兼顾计算效率,因此,选择中等密度、网格数为8 万的网格进行后续计算。
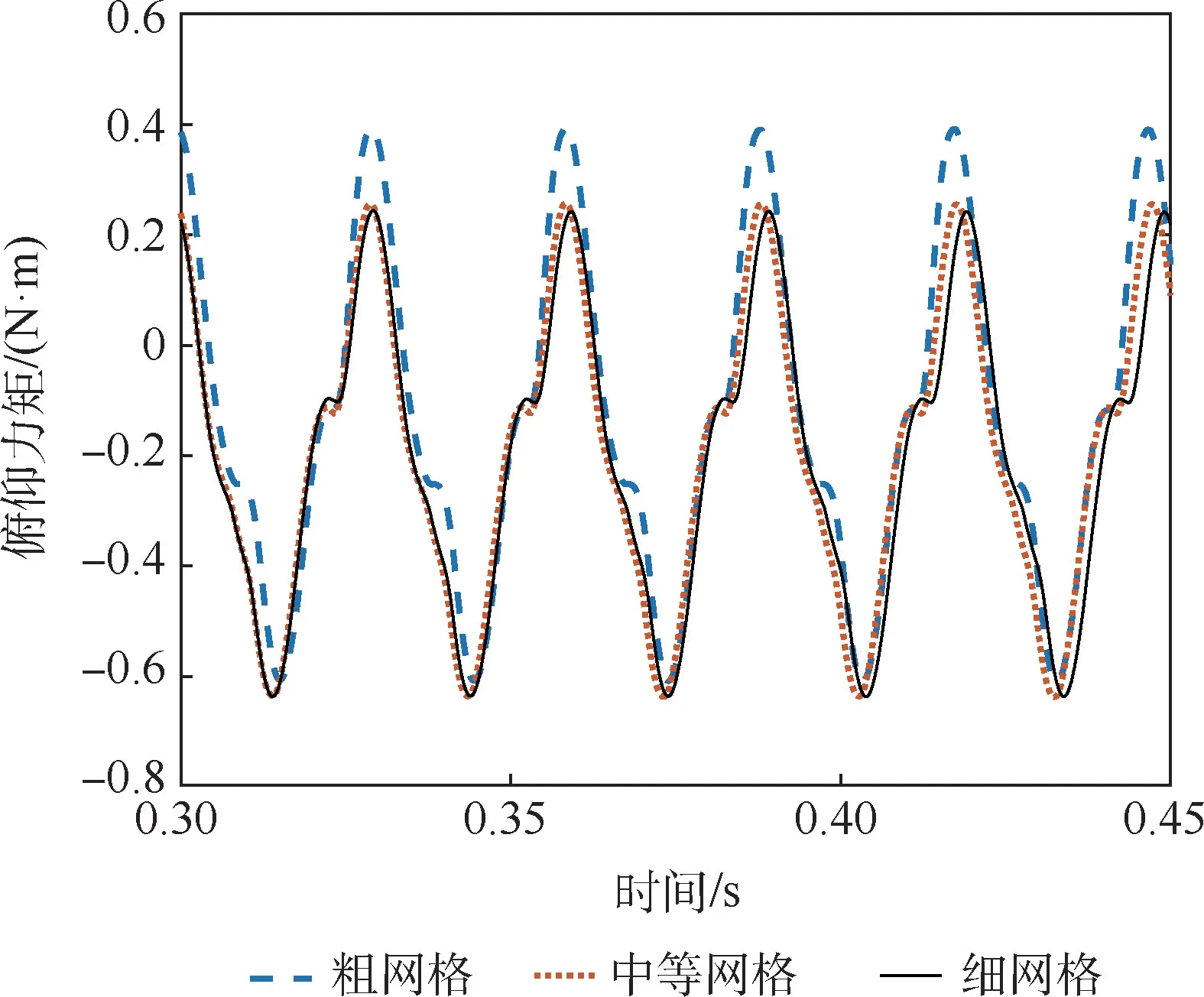
图4 三套网格的俯仰力矩随时间变化曲线Fig.4 Pitching moment of three grids versus time
2 DMD 方法
对于某个流场来说,一系列时间间隔为Δt的流场快照矩阵可以用前N+1 个时刻的流场信息向量xi表示为
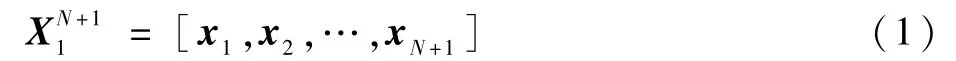
DMD 方法的基本思想是用一个线性算子来近似复杂流动的演化。 也就是寻找一个矩阵A,使得=,这样矩阵A就代表了相邻2 个时刻流场之间的线性关系。 但是在实际计算中,矩阵A是一个高维矩阵,因此,DMD 方法需要用一个低维矩阵来近似代替A。

式中:U、V为酉矩阵;Σ为奇异值对角矩阵;V*为V的共轭转置矩阵。
从而矩阵A的近似矩阵可以表示为


该模态对应的增长率gi和频率ωi分别为

式中:Re 为复数的实部;Im 为复数的虚部。
3 DMD 结果分析
对5°、10°、20°开裂角状态下的二维阻力舵模型进行非定常气动力计算,在流场稳定后提取网格节点处的压强数据。 对采集的流场数据进行DMD 分析。
图5 为来流10 m/s、开裂角5°状态下的原流场及前15 阶DMD 模态重构的流场压强云图,重构流场与原流场基本一致,图6 为DMD 分解得到的前4 阶流场模态,均为稳定的周期模态。

图5 流场压强云图Fig.5 Pressure contours of flow field
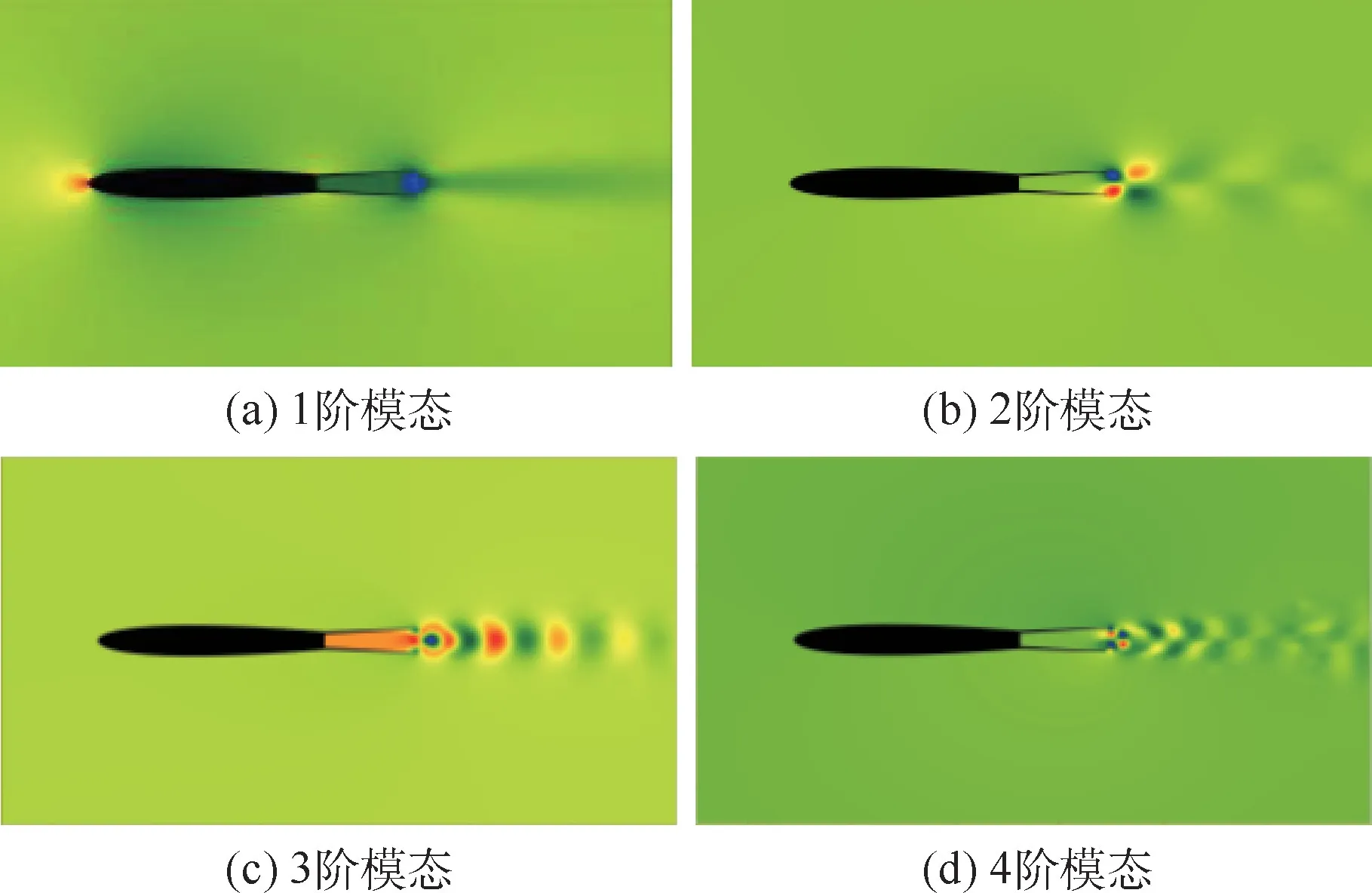
图6 开裂角5°前4 阶DMD 模态压强云图Fig.6 Pressure contours of the first four DMD modes at crack angle of 5°
各阶模态的增长率与频率数据如表1 所示。

表1 前5 阶DMD 模态增长率与频率Table 1 Frequency and magnification of the first five DMD modes
DMD 的1 阶模态表示频率为0 Hz 的平均流场,2 阶模态体现了阻力舵的上下后缘位置交替出现了脱落涡。 这2 个模态代表了流场的主要特征。 可以看出,3 ~5 阶模态频率大致为2 阶模态的整数倍,这说明DMD 分解捕捉到了流场的主要结构,同时提取到了高阶谐波模态。
图7 展示了一个周期T内开裂区的流场演化过程。 可以看到,在开裂区内部共存在a、b、c这3 个涡,其中,a是一直存在于开裂区内的驻涡,b、c分别为上下舵面后缘位置生成的脱落涡,它们分别与流场1、2 阶模态对应。 在0 ~T时段,涡b从上舵面后缘脱落进入流场,涡c由开裂区内逐渐向下舵面后缘移动;时段,涡b离开后缘位置进入流场,涡c继续向后缘移动,涡量逐渐增强;时段,随着涡c向后移动,上舵面逐渐生成了一个新的涡b;T~1T时段,涡b向后缘移动,同时新的涡c也在下舵面开始形成。
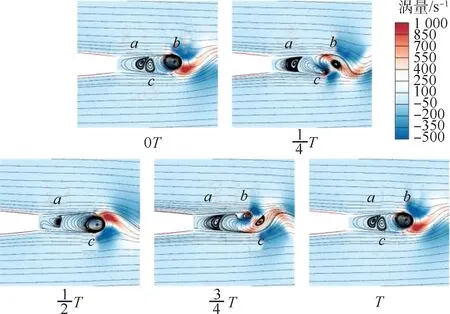
图7 流场演化过程Fig.7 Flow field evolution
对不同来流速度下的流场数据进行分析,结果发现,当来流速度在10 ~60 m/s 时,前5 阶流场模态云图基本一致。 不同来流速度下的DMD模态频率如图8 所示。 可以看出,随着来流速度增加,各阶流场模态频率基本线性增加,且高阶模态频率增加的更快。

图8 不同来流速度下的DMD 模态频率Fig.8 Frequencies of DMD modes versus velocity
在来流速度10 m/s 的状态下,分别对5°、10°、20°开裂角时的DMD 流场模态分解结果进行分析,频率分解结果如图9 所示。 开裂角的增大引起尾流区、回流区的范围变大,但流场结构没有太大差别。
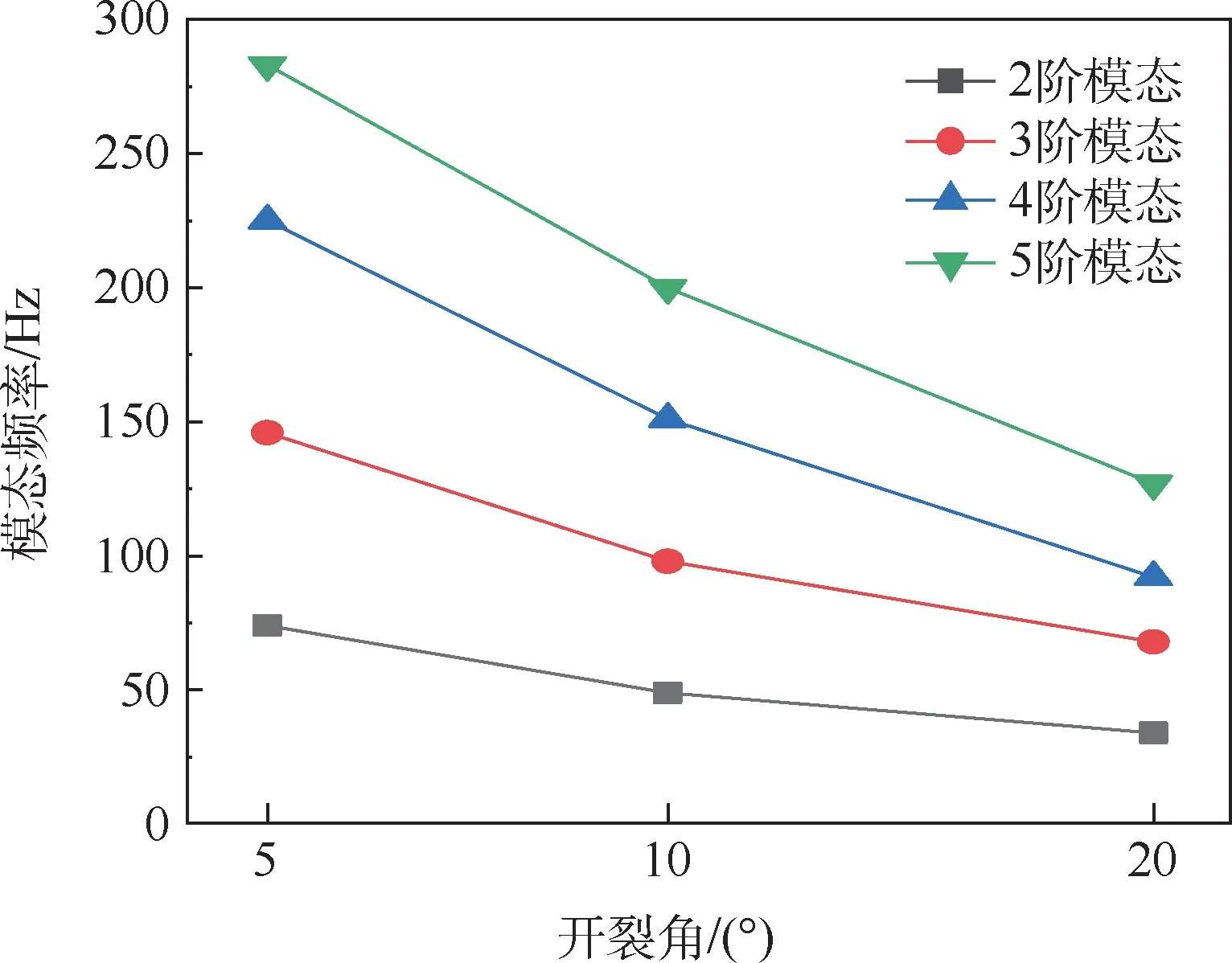
图9 不同开裂角下的DMD 模态频率Fig.9 Frequencies of DMD modes versus crack angles
DMD 分析的结果表明,在给定的速度范围内,流场结构主要表现为开裂区内驻涡与后缘脱落形成的卡门涡的叠加。 由于卡门涡的频率与速度成正比,与物体垂直于来流方向截面的特征尺度成反比,从图8 中的数据可以看出,在固定的开裂角下,DMD 模态频率与来流速度基本呈线性关系; 而图9 则说明了在相同来流速度下,随着开裂角的增大,翼型垂直来流方向的截面长度增加,因此流场模态频率随之下降;2 组结果反应出流场频率与流速和开裂角相关,不同DMD 模态之间频率的增长率不同。
4 流固耦合稳定性分析
当涡脱落的频率降低至与结构的固有频率靠近时,有可能会激发结构的振动,引发流固耦合系统的失稳。
使用Fluent 六自由度求解器进行结构求解计算,在模型的0.5 倍弦长位置安装扭转弹簧。 设置模型的惯性矩I为0.001 35 kg·m2,给定来流速度V为10 m/s,初始迎角为0.5°。 结构固有频率fn可由结构惯性矩I与弹簧刚度K得出:

无阻尼系统俯仰运动方程可以表示为

式中:M为流场计算得到的气动力矩;¨α为俯仰位移。
4.1 5°开裂角阻力舵流固耦合响应分析
图10 为5°开裂角的模型在不同的结构固有频率下俯仰角及俯仰力矩随时间变化的结果,其中f为频域分析中的频率。 从图10 中的结果来看,结构固有频率为6.6 Hz 时,结构响应的主要频率约为67 Hz,α的运动幅值很小,约为0.02°。这与表1 中流场2 阶DMD 模态的频率结果基本一致,因此,可以判断这是由于卡门涡的周期性脱落造成的涡致振动。 而当结构的固有频率为6.2 Hz时,结构的运动频率约为2.5 Hz,α的运动幅值约为3°,涡致振动的影响基本可以忽略,系统处于失稳状态。 此时结构运动频率与固有频率不一致是由于翼型带来的气动附加刚度导致的。
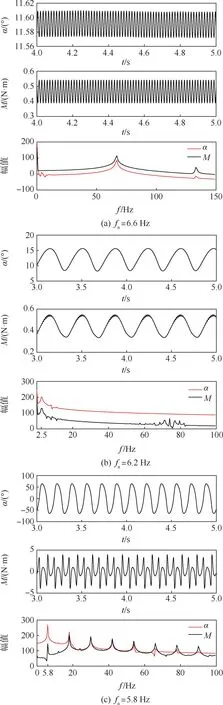
图10 不同固有频率下的响应曲线(5°开裂角)Fig.10 Response curves with different fn values natural frequency(crack angle is 5°)
定义无量纲的折减速度U*[22]为

式中:V为来流速度;fn为结构固有频率;c为翼型弦长。
由此可以得到一系列计算状态下系统的失稳频率fa随U*的变化规律。
对多个状态下的系统响应曲线进行分析,得到图11 所示结果。
从图11 中可以看出,模型的运动大致分为3个状态,当U*较小时,系统不会发生失稳,而是做小振幅的涡致振动,运动频率与涡脱落频率一致。 随着U*增大至5.2 ~5.7 之间,结构的运动形式表现为“浅失速”下的失速颤振,此时流固耦合系统在一定幅值下作俯仰振荡。 由于气动刚度的影响,系统的运动频率略低于结构的固有频率[23]。 当U*继续增大,系统进入“深失速”颤振状态,此时的运动频率约在6 Hz 左右。 这是由于系统无阻尼,同时结构刚度比较小,运动幅值较大,此时的流场特性占主导。 由于来流速度不变,在运动过程中前缘涡以6 Hz 左右的频率脱落、再附,结构响应频率也在6 Hz 左右。
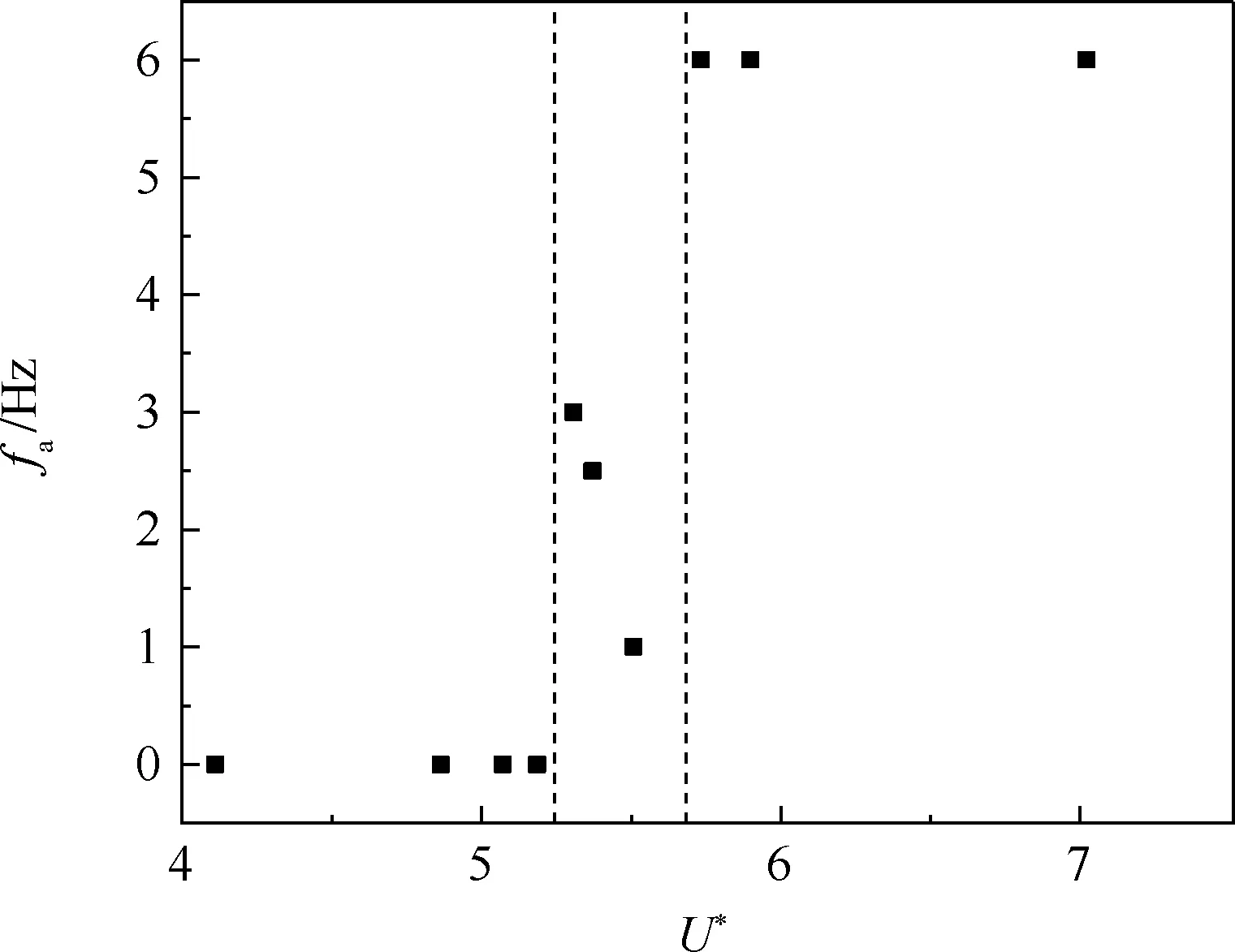
图11 系统失稳频率随折减速度变化(5°开裂角)Fig.11 Instability frequency variations with U*(crack angle is 5°)
4.2 20°开裂角阻力舵流固耦合响应分析
当开裂角为20°时,运动规律如图12 所示。该状态下的运动与5°开裂角相似,结构固有频率为6.1 Hz 时,运动形式为涡致振动,其频率与流场DMD 的2 阶模态一致,为30 Hz 左右,振动幅值很小。 当结构固有频率为5.3 Hz 时,系统运动形式为流固耦合失稳,频率大约为1 Hz,α的运动幅值在15°左右。
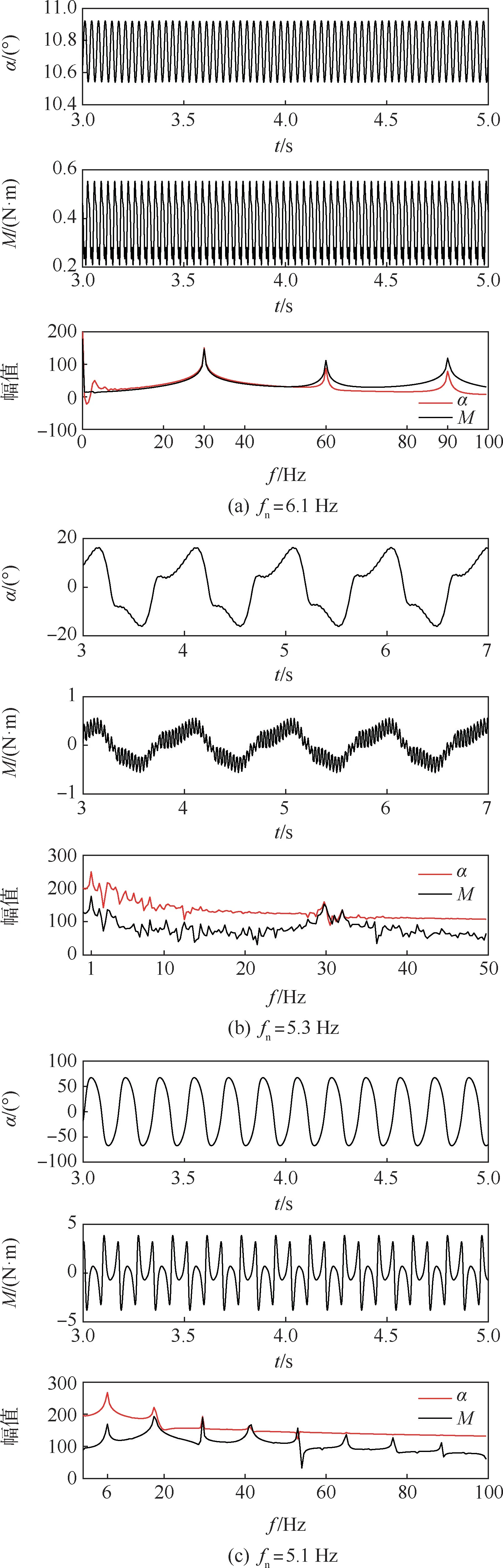
图12 不同固有频率下的响应曲线(20°开裂角)Fig.12 Response curves with different natural frequency(crack angle is 20°)
图13 展示了开裂角20°时fa随U*的变化情况,其规律与5°开裂角基本一致。 但是系统发生失速颤振时,折减速度的范围在5.6 ~6.4 之间,高于5°开裂角的状态。 这个现象说明,在阻力舵打开的过程中,系统的颤振边界提高,也就意味着在大开裂角状态下,阻力舵系统具有更好的稳定性。
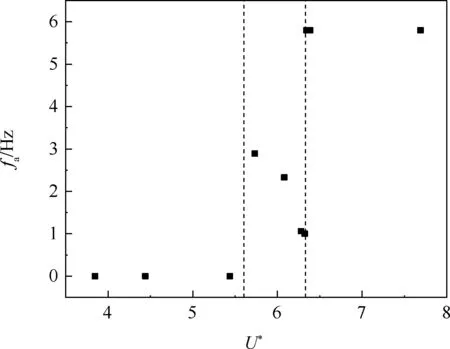
图13 系统失稳频率随折减速度变化(20°开裂角)Fig.13 Instability frequency variations with U*(crack angle is 20°)
5 结 论
1) 采用DMD 方法对二维阻力舵的流场特性进行探究,结果表明二维阻力舵流场的主要特征为开裂区的驻涡与后缘脱落涡的叠加。 流场的DMD 模态频率与来流速度成正相关,与开裂角的大小成负相关。
2) 进行阻力舵单自由度流固耦合运动仿真计算,结果表明,随着折减速度的增加,系统运动的主要形式由涡致振动发展为失速颤振,涡致振动的幅值远远小于失速颤振。 颤振边界随着开裂角的增大而减小,这表明增大开裂角对提高系统的失稳边界有着积极作用。
