机场到港旅客换乘时间效率评价指标优选

罗谦, 李琦, 文涛, 陈丰华, 朱萍

(1. 西华大学 计算机与软件工程学院, 成都 610039; 2. 中国民用航空总局第二研究所, 成都 610041;3. 广州白云国际机场股份有限公司, 广州 510000; 4. 重庆医科大学 教务处, 重庆 400016)

机场地面交通中心(ground transport center,GTC)是空港综合交通枢纽的重要组成部分,是旅客换乘的服务载体,到港旅客的换乘时间效率是决定GTC 换乘服务品质的核心要素之一,直接影响着旅客的换乘体验。 2021 年,中共中央、国务院印发的《国家综合立体交通网规划纲要》指出,预计2021—2035 年旅客出行量年均增速为3.2%左右,民航出行占比不断提升。 民航旅客出行量的逐年增加必然会促进GTC 飞速发展,对GTC的换乘效率无疑会是重大考验。 掌握到港旅客换乘时间效率情况对于提升GTC 的换乘效率有着重大意义,因此迫切需要构建一套科学实用的指标体系,以便对其做出客观正确的评价。

指标优选是指标体系构建过程中的核心关节,目的是通过计算指标数据关系,筛选出“低冗余、高影响”的指标,确保指标体系构建的科学性和合理性。 国内外学者们对此展开了大量的研究,并取得了一定的成果。 李盛阳等[1]通过计算指标扰动对目标值的影响情况来优选指标。 丛玮等[2]采用灰色关联聚类的方法计算指标与指标之间的灰色绝对关联度,筛选最具代表性的指标。Tang 等[3]使用特征提取的方法,从指标集中提取符合要求的指标。 杨柳等[4]通过信息融合的方法计算指标可信度,根据指标可信度对指标进行排序和优选。 张耀天等[5]提出了一种基于层次分析法的可变权重决策方法,对评价指标的权重进行动态修正,降低区分度不高的指标权重,提升区分度高的指标权重。 Zhu 等[6]使用主成分分析法(principal component analysis, PCA)对指标数据集降维,从大量冗余的指标中筛选出部分关键指标。 王丽萍等[7]将PCA 中的协方差矩阵替换为最大互信息系数矩阵,筛选强相关因子。 徐春荣等[8]在专家评分的基础上使用群组决策最大特征根法对指标进行初步筛选,并对初选指标进行相关性分析得到优选的指标体系。 迟国泰等[9]根据指标间相关系数剔除冗余指标,使用PCA 的因子负载来判断剩余指标对评价结果的影响程度,进而得到优选指标。 Zhang[10]根据文献研究法、问卷调查法、专家咨询法等方法对指标的影响因素进行分析,使用DS 证据综合法构建群体决策综合判断矩阵,并结合层次分析法确定指标权重筛选指标。

上述方法虽能达到指标优选的目的,但应用在民航机场到港换乘评价时,仍存在2 个问题:①量化指标数据关系时未紧密结合指标体系结构特征,指标关系反映不够精确,据此得到的指标排序还有优化的余地;②传统指标优选方法常依据经验制定指标筛选规则,缺乏理论支撑,优选模型有待完善。 针对以上问题,本文首先从指标体系结构特征中抽象出重要性、关联均衡性、独立性三重数据关系,使用DS 证据理论融合得到指标综合关系,根据指标综合关系得到更优异的指标排序。 然后,基于指标排序和综合评价方法,定义评估精度并设计优选算法完善优选模型。 最后,通过国内37 个机场的到港旅客换乘时间数据实证分析验证模型的有效性,同时构建科学合理的到港旅客换乘时间效率评价指标体系。

1 指标数据关系量化

当前,应用最广泛的指标体系是立体化塔式结构的3 层指标体系(目标层、因素层、指标层),传统平面化的计算方法难以全面、真实地反映3 层结构指标体系的数据关系。 本文将指标体系

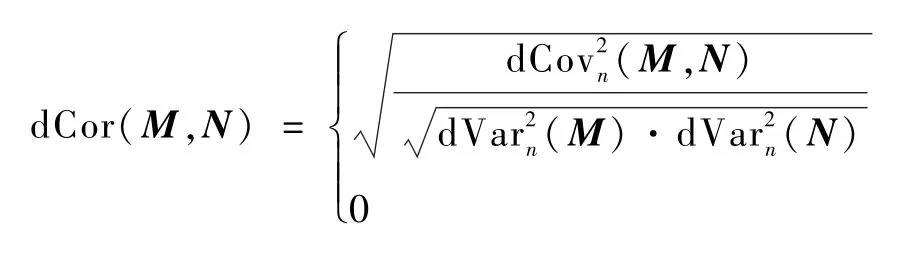
升序排列指标xi对各个因素的关联度表示为qi1,qi2,…,qig,关联均衡性Gi为

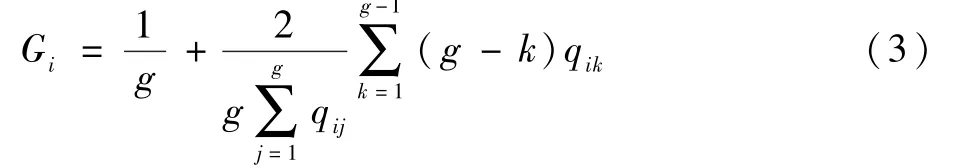
式中:j=1,2,…,k,…,g,g为因素个数;qij、qik分数据关系和指标体系结构特征相关联,从3 层结构指标体系的目标(Y)、因素(Yj,j∈[1,g];g为因素个数)、指标(xi,i∈[1,m];m为指标个数)中对应抽象出指标与目标、指标与因素、指标与指标之间的3 种数据关系,分别表示为:xi↔{x1,x2,…,xm};xi↔Yj,i∈[1,m],j∈[1,m];xi↔xk,i∈[1,m],k∈[1,m]。 3 种数据关系分别反映指标的重要性、关联均衡性和独立性,根据各自特点采取不同方法量化,从而形成全方位、立体化的指标数据关系量化方法。

1.1 重要性

重要性诠释的是指标对目标的影响程度。PCA[5]不仅能够用于降维,其因子载荷矩阵[6-7]也能反映出指标对目标的影响情况。 使用PCA来量化指标与目标之间的数据关系,将指标在各个主成分上因子载荷的绝对值作为指标重要性的评分,值越大,表示该指标对目标影响越大。

首先,将指标数据集标准化,并得到其协方差矩阵Pm×m,m为指标个数。 然后,由P-λa=0得到P的特征值λ及单位特征向量a,并将特征值λi按照大小排序,使得λ1≥λ2≥…≥λm≥0。

设指标xi在第j主成分上因子载荷为bij,则指标xi重要性的计算公式为

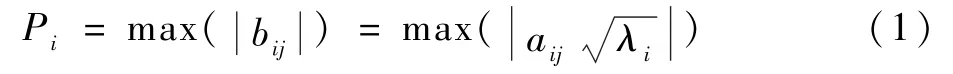
1.2 关联均衡性

关联均衡性诠释的是指标和因素之间的关联情况。 使用距离相关系数[11]计算指标和因素的关联度,引入Gini 系数计算关联度的均衡性[4],关联度越均衡,则指标和因素的关系越稳定。

设有矩阵M、N,其样本距离协方差和样本距离方差分别为和,则有M、N的关联度dCor(M,N)为别为指标xi对因素j、k的关联度。

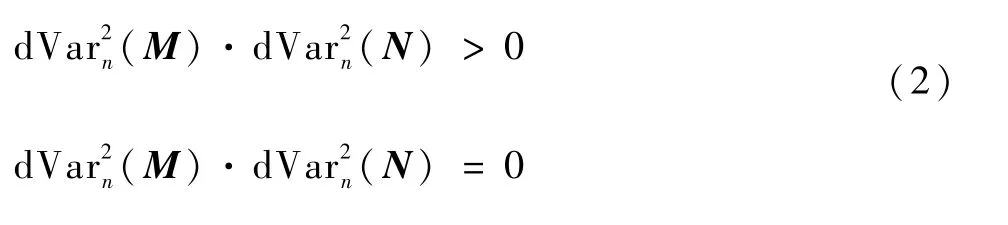
1.3 独立性

独立性诠释的是指标和指标之间的依赖关系,独立性越强,表明指标的依赖越低,越应该保留。 使用最大互信息系数[3](maximal information coefficient, MIC)计算指标和指标之间的相关性来表示指标之间的依赖情况。

给定2 个随机连续变量α和β,假设其概率密度分别为p(α)和p(β),联合概率密度为p(α,β),则α和β之间的互信息I和最大互信息系数MIC 分别为

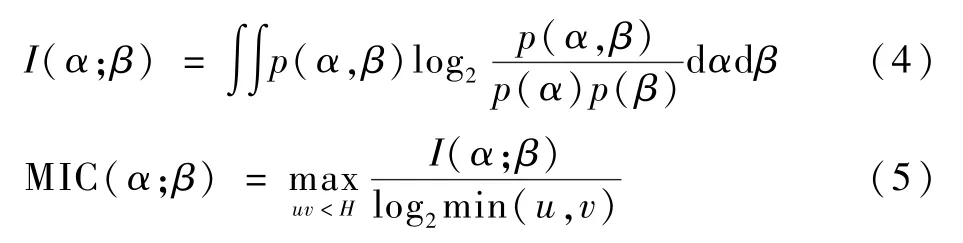
式中:u、v分别为在α、β方向上划分格子的个数;H取值为数据量的0.6 次方。

指标xi独立性计算公式为

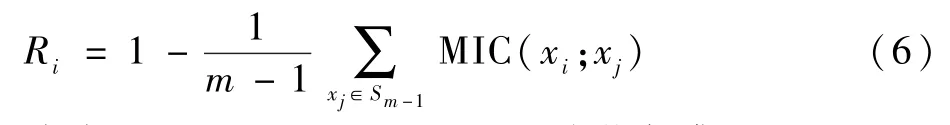
式中:xi∈Q;Sm-1=Q-xi;Q为指标集。

2 基于指标综合关系的优选模型

2.1 指标综合关系

结合指标体系结构特征抽象出来的3 种指标数据关系,一定程度上反映了不同层面的业务关系,3 种数据关系的量化结果可以视为“专家”在不同维度对各个指标的评价值,为了消除“专家”之间的“偏见”,使用DS 证据理论将其融合得到指标的综合关系。 3 种数据关系的定量表示视为DS 证据理论的基本概率赋值函数[12](basic probability assignment, BPA),融合结果视为指标综合关系的量化值。

为了解决DS 证据理论融合过程中证据冲突的难题,使用相容系数[13]优化证据可信度[14]来避免证据冲突。

设识别框架Θ=(A1,A2,…,Aη),证据集E=(E1,E2,…,Eω)对应的BPA 为m1,m2,…,mϖ, 定义证据距离矩阵Dϖ×ϖ= [dij]ϖ×ϖ,其中,dij由相容系数计算得到

式中:ϖ为证据个数;si∈[0,1]。si的大小反映的是证据Ei与其他证据之间的差异程度,si较大时,差异较大,可信度因子εi较小;反之,则差异较小,可信度因子较大。 即si→1 时,εi→0;si→0 时,εi→1。

设εi=f(si),则f(si) 应满足如下条件:①f(si)是单调递减函数;②si较小时f(si)衰减缓慢,si较大时f(si)迅速衰减到零。 综上,f(si)应是一条指数相关单调递减曲线,则可定义可信度因子为

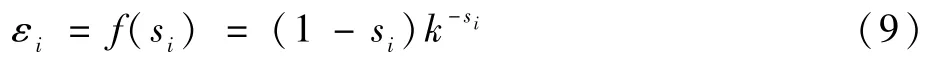
当k= 2. 965-1时,关系曲线最符合要求,则有

设原始证据的BPA 为mi(Aj),修正后的BPA为m″i(Aj),则有

指标综合关系充分考虑了指标的业务关系和数据关系,能够真实反映指标的重要程度,得到优异的指标排序,为指标优选提供了依据。

2.2 优选模型

2.2.1 筛选指标的判定规则

设评价对象集为Y= [y1,y2,…,yn],n为评价对象数量;原始指标集为X= [x1,x2,…,xm],m为原始指标集的指标总数;优选指标集为Xopt;根据指标综合关系将原始指标集降序排序得到排序指标集Xorder;取排序指标集中前k(k≤m)个指标得到评价指标集, 表示为Xorder-k。

指标优选希望使用比原始指标集更少的指标得到相同甚至更优的评价结果。 但一方面,指标数量越多,涵盖目标的信息就越广,试图使用少量的指标得到更优的评价结果显得不切实际。 另一方面,指标之间存在冗余,剔除冗余指标后进行评价,得到与使用原始指标集相同的评价结果却是切实可行的,指标优选的意义即在于此。因此,本文以使用原始指标集的评价结果作为基准,将使用评价指标集的评价结果与之比较,衍生出评估精度的定义,作为指标筛选规则的理论支撑。

为使得筛选指标的标准有效且统一,需要使用综合评价方法进行评价,使用聚类方法给评价结果聚类并据此给评价对象赋标签。 综合评价研究中常采用5 类标签[15]或3 类标签[16],5 类标签标示优、良好、一般、较差、差,3 类标签标示好、中、差。 现有综合评价方法适用条件不同且各有利弊[17],其中熵权TOPSIS 方法[18-20]具有原理简单、数据利用充分、可防止人为赋权影响评价结果等优点,因此本文采用该方法进行综合评价。 为了兼顾各分类中指标的范围和数量尽量相近,采用自然断点法[21]做为聚类方法。

定义1标签集。 标签集是换乘时间效率评价结果的集合,可表示为Fk= [fk1,…,fki,…,fkn]。 其中,n为评价对象个数,k为评价指标集中指标个数;fki表示第i个评价对象的标签值,若是5 类标签,fki∈{1,2,3,4,5},若是3 类标签,fki∈{1,2,3}。

定义2评估精度。 记使用原始指标集进行评价得到的各评价对象的标签值为fmi,设c为Fk中满足fki=fmi的个数,评估精度A可表示为

由于评估精度的定义是以使用原始指标集的评价结果作为基准,当k=m时,A=100%,评估精度必然能够达到100%。 若当k＜m时,A=100%,则可剔除m-k个指标,可以预见的是,指标排序越优异,A=100%时k越小,能够剔除的指标越多。

综上,指标筛选规则为:当评估精度达到100%时,评价指标集即为优选指标集,不在评价指标集之内的指标即可予以剔除。

2.2.2 算法设计

精确全面的指标关系和科学严谨的优选算法是影响指标体系科学性的两大关键点。 目前,大多数学者聚焦在指标关系研究上,缺乏对优选算法的研究。 本文基于指标综合关系和评估精度设计优选算法,从原始指标集中筛选优异指标形成优选指标集,完善优选模型。

优选算法具体步骤如下:

步骤1基于原始指标集X,使用熵权TOPSIS 评价模型综合评价各个目标对象,使用自然断点法将评价结果聚类并据此给评价对象赋予标签,得到基准标签集Fm,令k=1。

步骤2从排序指标集Xorder中取出k(k≤m)个指标形成评价指标集Xorder-k。

步骤3基于Xorder-k,使用熵权TOPSIS 评价模型综合评价各个目标对象,使用自然断点法将评价结果聚类并据此给评价对象赋予标签,得到标签集Fk。

步骤4基于Fk和Fm,计算Xorder-k的评估精度。

步骤5如果评估精度为100%,跳转到步骤6;否则,令k=k+1,跳转到步骤2。

步骤6优选指标集Xopt=Xorder-k, 结束。完整优选模型如图1 所示。

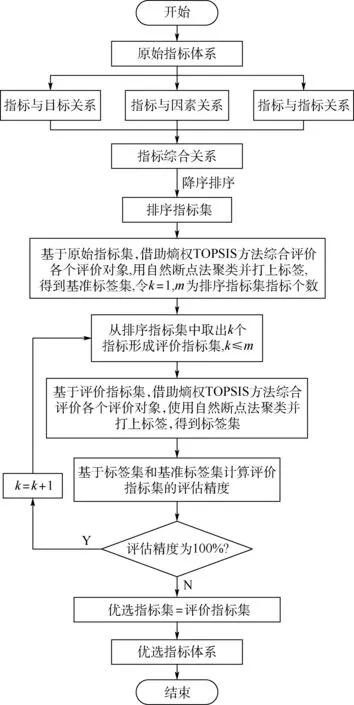
图1 完整优选模型流程示意图Fig.1 Flow diagram of complete optimization model

3 实证分析

3.1 原始指标体系与实验方法

为验证优选模型的有效性,构建科学实用的到港旅客换乘时间效率评价指标体系,根据到港旅客换乘业务特征,将其分为5 个阶段:落地等待、下机摆渡、至行李转盘步行、行李等待、候车。 分别从换乘时间、旅客满意度、预期达标率(可容忍换乘时间内完成换乘的人数占总人数的比率)3 个方面共提取出15 个指标来反映各个机场对于到达旅客换乘时间效率的综合情况,构建出3 层结构的原始指标体系,如表1所示。

表1 原始指标体系Table 1 Original index system

结合原始指标体系结构特征抽象出3 种数据关系。 指标与目标、指标与因素、指标与指标之间的数据关系可分别表示为:xi↔{x1,x2,…,x15},i∈[1,15];xi↔Yj,i∈[1,15],j∈[1,3],Y1= [x1,x2,x3,x4,x5],Y2=[x6,x7,x8,x9,x10],Y3=[x11,x12,x13,x14,x15];xi↔xk,i∈[1,15],k∈[1,15]。

按照5 类标签和3 类标签进行2 组实验,在这2 种情况下分别采用PCA 和MIC 方法计算指标关系与本文的指标综合关系进行优选对比,分析评估精度达到100% 之后的情况。 从CAPSE报告[22]中收集37 个国内机场的到港旅客换乘时间数据进行实验。

3.2 结果与分析

将3 种数据关系视为3 个证据,根据指标数据关系量化方法量化,结果视为各自证据的BPA,使用式(11)对BPA 进行修正,将修正之后的BPA 使用DS 证据理论融合,得到指标综合关系,将指标按照指标综合关系的量化结果排序(见表2)。

由表2 可以看出,行李等待阶段提取的指标在各自因素内排序都是最末,而候车阶段提取的指标在各自因素内排序都较为靠前,这与实际情况相符。 随着智慧机场建设的逐步推进,行李分拣系统等一系列智能系统的广泛应用缩短了旅客等待行李的时间,行李等待时间已不是影响旅客换乘时间效率的关键因素。 而由于GTC 换乘的复杂性,各种交通工具的协调运行控制仍然是一大难题,候车时间仍是旅客关注的重点,极大地影响着到港旅客的换乘时间效率。 在指标综合关系量化结果的指导下,行李等待时间满意度指标x9的指标综合关系值最低,代表在考虑指标的重要性、关联均衡性、独立性之后,指标x9的可保留性最低。 但是否剔除指标x9,不能依据主观臆测,应根据评估精度,比较指标在评估中的作用来判断。

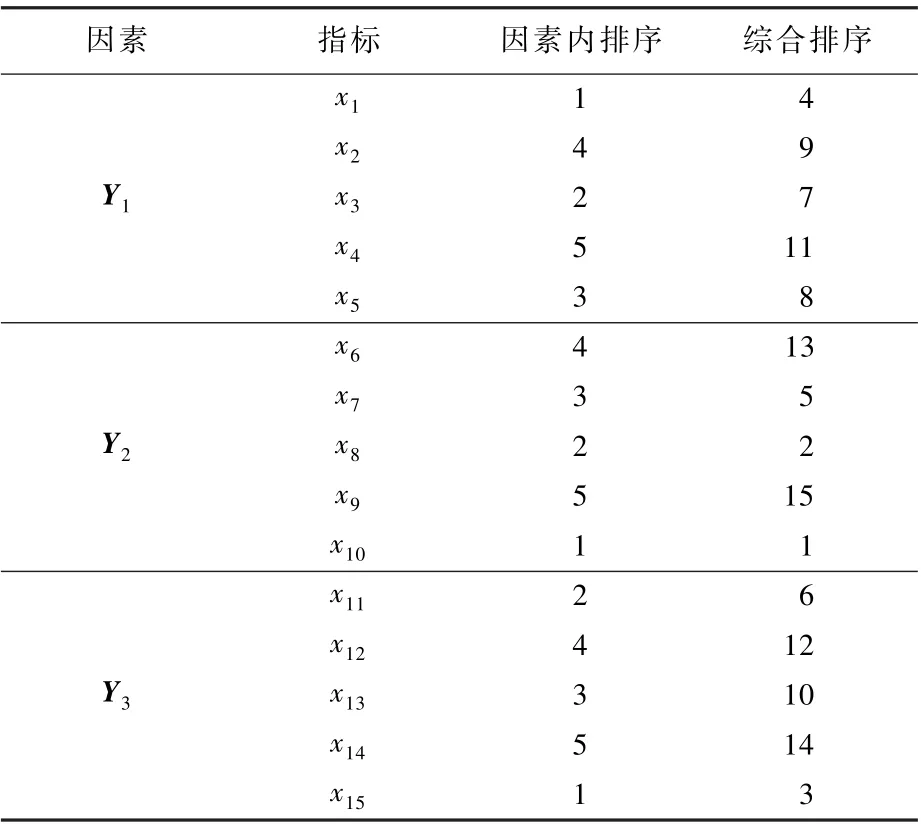
表2 指标综合关系量化结果排序Table 2 Ranking of quantitative results of comprehensive index relationship

分别在5 类标签和3 类标签的情况下,基于指标综合关系、PCA 指标关系、MIC 指标关系使用本文优选算法计算评估精度,比较评估精度达到100% 之后的情况。 其中, PCA 的阈值取85%,即当累积方差贡献率达到85% 时,提取主成分,计算各指标在主成分上的因子载荷作为PCA 指标关系[9]。 过往经验表明[7],MIC 的网格数取15 × 15 时能取得较好的效果,即式(5)中H=0.6,u=v=15。 对比实验结果如图2 和图3所示。

图2 五类标签下评估精度结果比较Fig.2 Comparison of evaluation accuracy results under five kinds of labels

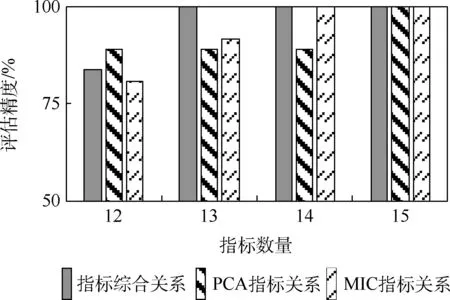
图3 三类标签下评估精度结果比较Fig.3 Comparison of evaluation accuracy results under three kinds of labels

图2 和图3 都能看出,当评估精度达到100%之后,再增加指标并不会影响评价结果,也就是说余下的指标均可剔除。 图2 表示,5 类标签情况下,根据指标综合关系得到的指标排序,使用前14 个指标达到了评估精度的100%,可剔除最后一个指标,而此时依据PCA 指标关系和MIC指标关系得到的指标排序,使用优选算法则无法剔除冗余指标,没有体现出优选效果。 3 类标签相较5 类标签容错的阈值更广,因此有机会剔除更多的指标。 图3 表示,3 类标签情况下,根据指标综合关系得到的指标排序使用前13 个指标达到了评估精度的100%,可剔除后2 个指标,此时基于PCA 指标关系得到的指标排序仍然无法剔除指标,基于MIC 指标关系得到的指标排序只能剔除1 个指标。 上述实验结果表明,将指标体系数据关系和指标体系结构特征结合起来抽象出的重要性、关联均衡性、独立性反映了指标不同层面的特性,融合三者得到的指标综合关系比单一的PCA、MIC 方法得到的指标关系更加真实准确,排序结果更加优异,在100% 评估精度的情况下能够剔除更多的冗余指标,具有更好的优选效果。此外,传统的指标优选算法常以经验制定优选规则,缺乏切实的理论支撑。 本文以原始指标集的评价结果作为基准,从指标优选的意义出发,定义评估精度作为筛选指标的理论支撑,据此提出优选规则及算法,完善了优选模型。 从图2 和图3即可看出,评估精度能够将可剔除的指标直观展示出来,筛选指标有据可依,优选结果清楚明晰。

综上,根据指标综合关系,在5 类标签情况下剔除指标x9,在3 类标签情况下剔除指标x9、x14,得到科学合理的到港旅客换乘时间效率评价指标体系。

4 结 论

本文为构建科学合理的换乘时间效率评价指标体系,基于指标综合关系构建优选模型来筛除冗余指标,研究结果表明:

1) 结合指标体系结构特征抽象出重要性、关联均衡性、独立性三重数据关系,融合得到指标综合关系,能够更加全面地反映指标关系,优化了指标排序。

2) 定义评估精度并设计优选算法完善了指标优选模型,使得在民航机场到港换乘评价领域中筛选指标能够有据可依,优选结果清楚直观。

3) 为空港GTC 的换乘时间效率评估提供了指标体系支撑,在北京首都国际机场、北京大兴国际机场的综合交通运行评估中得到实际应用。 第三方评估也可基于历史评估对象数据,采用本文模型优选指标构建指标体系,对现有评估对象做出科学合理的评价。

下一步考虑在本文构建的指标体系的基础上,结合数据特征和业务实际研究综合评价方法,并对各机场到港旅客换乘时间效率进行评价分析,提出相应优化建议。