基于动态四叉树搜索的民航行李车码放算法

2023-01-12邢志伟侯翔开李彪张涛文涛

北京航空航天大学学报 2022年12期

邢志伟, 侯翔开, 李彪, 张涛, 文涛

(1. 中国民航大学航空工程学院, 天津 300300; 2. 中国民航大学电子信息与自动化学院, 天津 300300;3. 中国民用航空局第二研究所工程技术研究中心, 成都 610041)

航空行李装卸与运输是机场运行保障的重要环节之一。目前,中国机场行李码放装卸仍以人工作业为主,存在效率低、空间浪费大等问题;少数大型机场高价购买国外行李码放系统,每年维护费用高昂。因此,民航行李码放的智能化与自主化将是中国民航行李处理的发展趋势。而行李系统的核心问题是其内部嵌入的码放算法。

民航行李车码放算法的本质某种程度来说可视为三维装箱算法,是典型的NP-hard 问题,此类问题在Dyckhoff[1]与Wäscher[2]等的关于切割和布局问题的综述中有详细的论述。在Bortfeldt 和Wäscher[3]更详细的分类中,行李车码放算法可被具体分入SKP(single knapsack problem) 问题。Fanslau 和Bortfeldt[4]将其按解决方法类型分为3 类:①经典启发式方法。具有代表性的为George 和Robinson[5]首次提出的砌墙算法及Crainic 等[6]提出的“关键点”算法。此类算法运算简单、速度快,但空间利用率不够理想,缺乏对稳定性的考虑,属于早期算法,是之后绝大多数算法的基础。 ②元启发式算法。将模拟退火算法、遗传算法等融入启发式算法得以形成。文献[7-9]中利用模拟退火算法通过不断跳出局部最优改善码放方案;文献[10-13]利用遗传算法找到组合最优解,其中,文献[13]的在线装箱算法更有利于解决现实问题;文献[14]运用了禁忌搜索算法;文献[15]运用了萤火虫算法。此类算法结果利用率高,但往往迭代次数多,运算速度慢。③树搜索算法。文献[4,16-20]是基于树搜索的三维装箱问题求解算法,以树搜索的思想选择不同阶段的码放方案。此类算法计算速度快、空间利用率高,但容易在搜索过程中因选择条件单一产生局部最优。

部分学者从现实应用的角度设计了相应的算法。例如,文献[21]对施加方向约束的大型集装箱装载问题开展了研究,算法更侧重于集重类货物装载;文献[22]专注于解决物流中的打包问题;文献[23]为港口集装箱优化了配载方案。可见,即使是针对现实约束的三维装箱算法,也大都集中于各类集装箱或大型车辆的装载,缺乏面向航空空间约束的民航行李运输研究。

因此,本文提出了一种以民航行李车装载为背景,结合四叉树搜索、动态规划与动态选择算法的民航行李车码放算法,并通过实际行李构型数据和同类算法的对比验证了算法的实用性。

1 问题描述

1.1 数学模型

如图1 所示,民航行李车的长、宽、高分别为L、W、H,体积为V。以民航行李车右后下点为原点,底面为xy平面,垂直底面向上方向为z轴建立坐标系。行李的长、宽、高分别为l、w、h,其体积为v,如图2 所示。 (xi,yi,zi)、(x′i,y′i,z′i)为行李i右后下、左前上坐标。给定行李车和一批待装入行李B={b1,b2,…,bn},ηi为判断行李是否装入的决策变量,若行李i已装入行李车,则ηi=1。装载要求为:在满足实际约束的情况下,得到使行李车空间利用率最大的码放方案。据此,目标函数如下:

图1 民航行李车示意图Fig.1 Schematic diagram of luggage cart for civil aviation

图2 行李摆放姿态Fig.2 Luggage placement

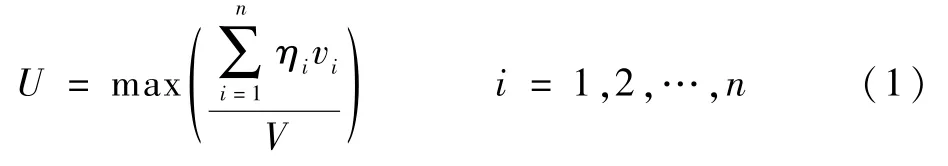
1.2 假设条件

基于航空行李的实际装载过程提出如下假设:

1) 形状均为长方体。

2) 在最大承重范围内可接受多层装载。

3) 不考虑装载过程中出现的挤压变形。

4) 密度均匀,重心位于其几何中心。

1.3 约束条件处理

航空行李装载有其自身独特的特点,如民航旅客行李平均价值高、对运输损失的容忍度低、装卸速度关系着旅客值机时间等。这些特点决定了行李装载独特的空间约束。因此,针对民航行李车码放问题,可以定义为:在行李集合中选出一个子集码放入行李车中,使行李车空间利用率最大,并满足以下约束条件:

1) 边界约束。码放在行李车中的所有行李都必须完全包含在行李车内,即

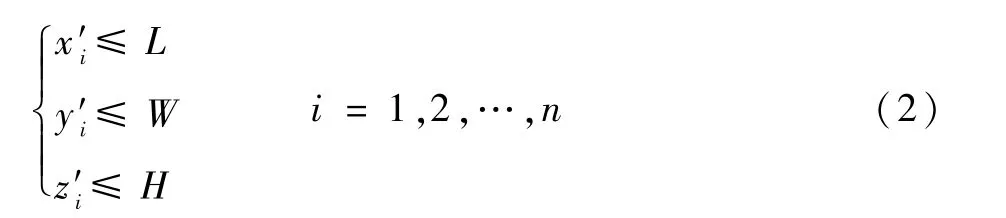
2) 不重叠约束。所有行李不得与其他行李存在重叠的部分,即

或

式中:“∨”代表“或”或者并集。

3) 方向性约束。所有行李只可以以最短边为垂直高度码放,即

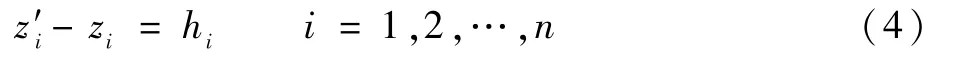
4) 稳定性约束。码放的行李受到其他行李顶面或行李车底部完全支撑,即当行李i放置于行李j之上时满足:

式中:“∧”代表“且”或者交集。

5) 完全切割约束。码放后形成的码放块可以通过多个竖直的平面分割成多个竖层,每个竖层可以通过多个水平的平面分割为最终的行李。所有用于分割的竖直平面与水平平面不能与对应的码放块中的行李相交,即

不存在。

2 动态四叉树搜索码放算法

2.1 算法原理

算法以四叉树为基本框架,在每层设计固定数量节点以提高搜索速度。算法码放界限为民航行李车C,其包含行李车的三维属性为长、宽、高,C= (L,W,H)。

算法搜索过程中的节点对应码放方案con,每层n个。 con 中包含剩余空间F、剩余复合条集合S、所用复合层P等, con= (F,S,P)。剩余空间F是在码放过程中对C完成码放后的剩余空间,尺寸为x_free、y_free,F= (x_free,y_free)。四叉树的顶点对应的码放方案状态为尚未开始码放。码放方案集合表示动态四叉树中所有继续搜索的节点,CON ={con1,con2,…,conn}。

以四叉树顶点即空码放方案为起始开始搜索,在码放方案中添加一个复合层pi生成新码放方案。pi是通过将复合条sj以相同的姿态沿x轴或y轴码放生成的。pi的x、y方向尺寸为其底面的最小外包矩形对应尺寸,高度为H。复合条sj是将多个行李b以动态规划的算法沿z轴码放得到的行李组合,如图3 所示。定义sj尺寸为其最小外包长方体尺寸,高度为H。sj=(Q,l_sj,w_sj)。其中,Q为包含b的集合,l_sj为sj的长,w_sj为sj的宽。行李bi包含行李的三维属性长、宽、高,bi=(li,wi,hi)为码放算法中的最小单元。

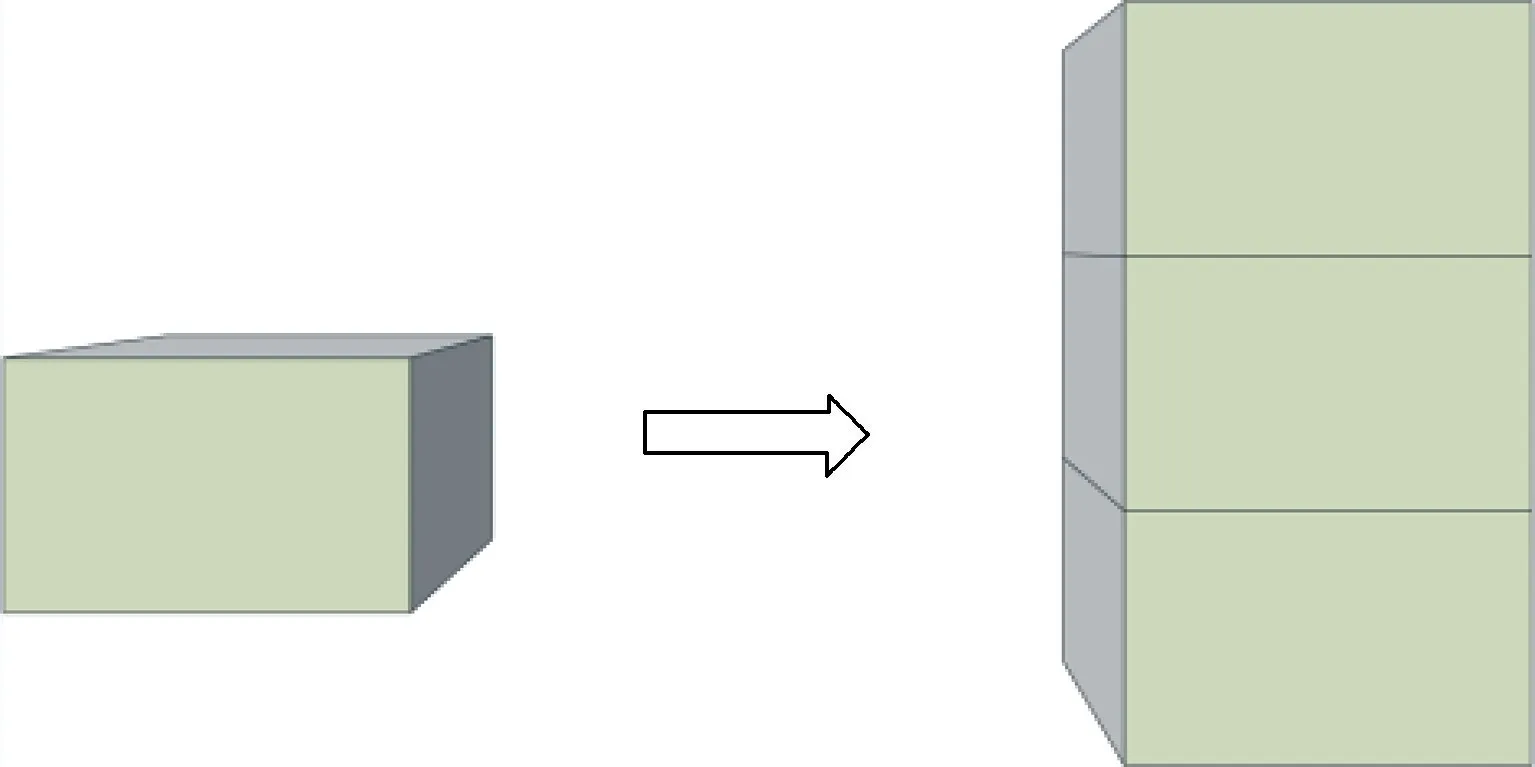
图3 复合条生成示意图Fig.3 Schematic diagram of compound bar generation

生成的sj以填充率fr_sj作为筛选的标准。fr_sj为sj内行李实际体积与定义体积的比值,计算公式如下:

式中:vs为复合条内行李的体积。

以所有行李生成复合条集合S= {s1,s2,…,sn},并通过动态规划算法组合sj生成pi。定义d为复合层的形状变量,代表不同复合层形状,d=1,2,3,4,如图4 所示。pi= (K,xl_pi,yl_pi,d),其中,K为包含的复合条集合,xl_pi为pi在x轴方向长度,yl_pi为pi在y轴方向长度。复合层集合P= {p1,p2,…,pn} 代表码放方案中的已码放结果。

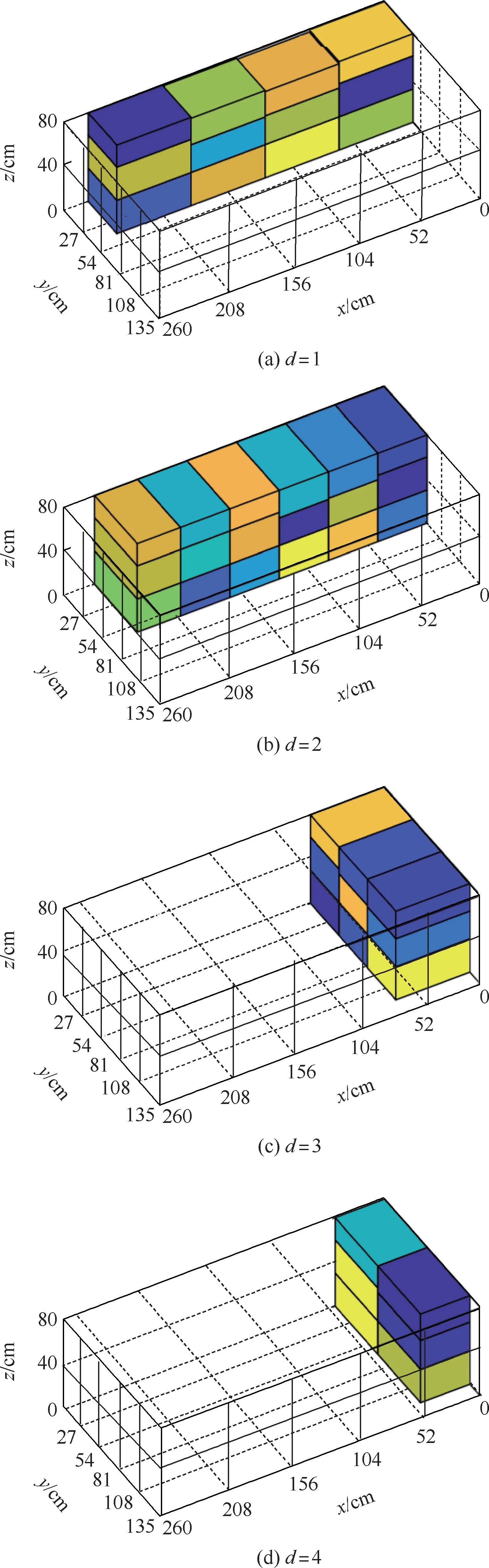
图4 四种复合层示意图Fig.4 Schematic diagram of four types of composite layers

复合层填充率fr_pi是算法搜索过程中选择新码放方案的标准之一,是pi内行李的实际体积与定义体积的比值,计算公式如下:

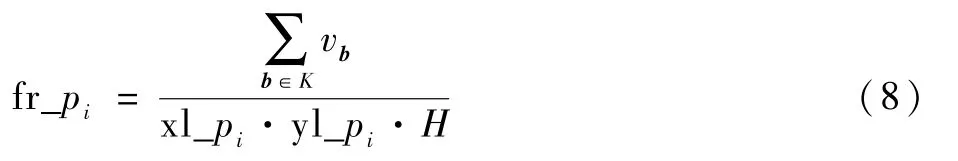
式中:vb为b的体积。

将pi放入con 即得到待选码放方案r。r与con 结构相同,包含剩余空间、剩余复合条集合、所用复合层等,r= (F,S,P)。con 添加的复合层有4 种,故r有4n个。在算法的搜索选择过程中,r成为新一代码放方案或被舍弃。

同一深度的con 生成的所有r放入待选码放方案集合R= {r1,r2,…,r4n} 中等待动态选择算法进行遍历选择,选出n个作为新一代码放方案。

如此迭代直至某个con 在算法的迭代过程中无法继续添加复合层或所有行李码放完成,将此码放方案称为最终码放方案,将其放入最终码放方案集合FINCON 中。

在算法开始搜索前会将S中底面积最小的一部分复合条先取出搁置,组成小型复合条集合Sl,占比为整体的25%。当con 中已码放的复合层占据空间超过C的一半时,将放入S中参与迭代,使用“填缝”的思想提升空间利用率。

当算法中不存在可继续搜索的码放方案时,算法结束。取FINCON ={con1,con2,…,conk}中空间利用率最高者为算法的最终输出结果。

2.2 算法流程

本文算法先将所有行李以动态规划的算法沿z轴组合成s放入S中。然后,基于剩余空间生成4 种复合层,并构造四叉树,如图5 所示,根节点为尚未开始码放的初始码放方案。根据设计的动态选择算法对四叉树迭代搜索得到最终码放方案。整个算法实现流程如图6 所示,以下介绍内嵌算法。

图5 四叉树搜索Fig.5 Quadtree search

图6 算法嵌套图Fig.6 Nesting diagram of algorithm

算法1动态四叉树搜索(dynamic quadtree search,DQS)算法。

算法为复合条生成和剩余空间装载,得到最终码放方案。

步骤1生成空的S、Sl、CON、R、FINCON。

步骤2调用复合条生成算法(算法5a 和5b),生成复合条并放入S中,取出其中底面积最小的前25%放入Sl。

步骤3调用剩余空间装载算法(算法2),得到FINCON。

步骤4在FINCON 中选取空间利用率最大的码放方案,算法结束。

算法2剩余空间装载(loadspace)算法。

算法为迭代算法,最终得到FINCON。该算法在码放后期利用Sl“填缝”更好地填充了剩余空间,如图7 所示。

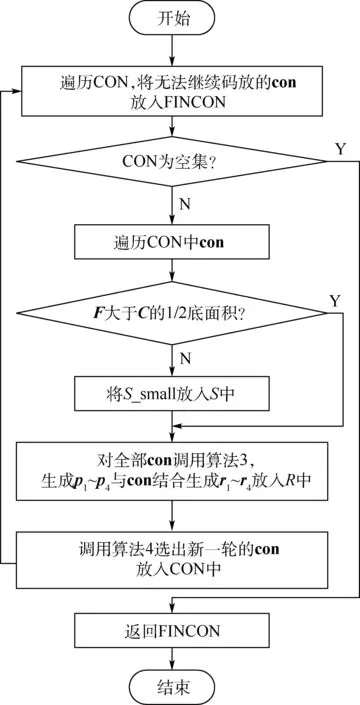
图7 算法2 流程Fig.7 Flow chart of algorithm 2

算法3复合层生成算法。

根据不同码放方案中剩余空间与剩余复合条集合的各项参数重新设定动态的最低空间利用率,提升整体利用率,保证运输过程的稳定性(见图8)。公式具体如下(以沿x轴码放为例):

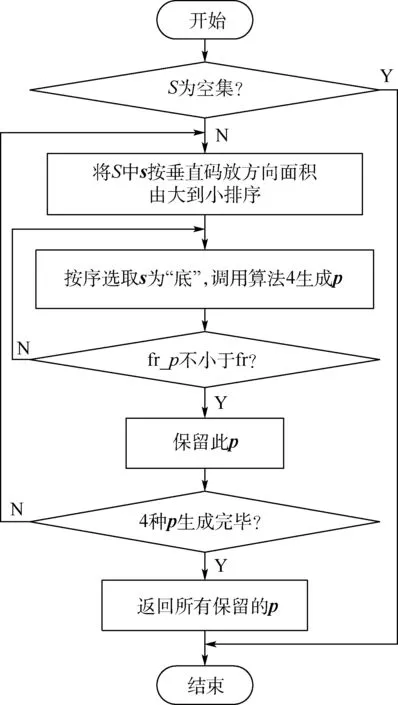
图8 算法3 流程Fig.8 Flow chart of algorithm 3

式中:fr 为复合层的动态最低空间利用率;fr0为复合层最低空间利用率上限;δ为剩余复合条长度标准差;m为剩余复合条数目;¯l为剩余复合条长度平均值;x_free 为剩余空间沿x轴方向的长度。

算法4动态选择算法。

如图9 所示,设计了一种基于剩余空间和剩余复合条集合双重因子影响的动态选择算法,并在每层选出n个继续搜索的码放方案。算法中存在2 个计算值,即实际浪费体积vact和潜在浪费体积vhide(见图10)。

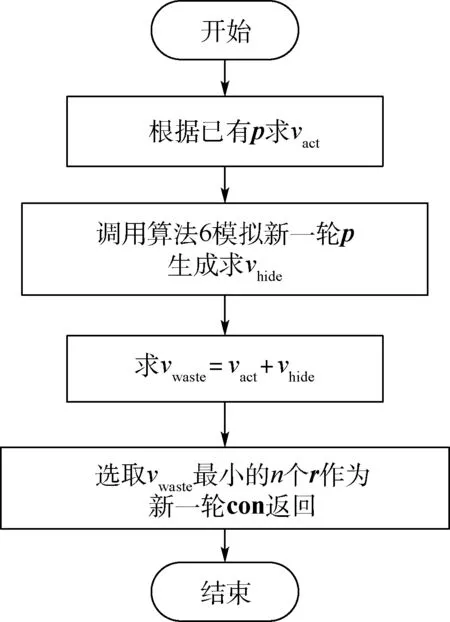
图9 算法4 流程Fig.9 Flow chart of algorithm 4

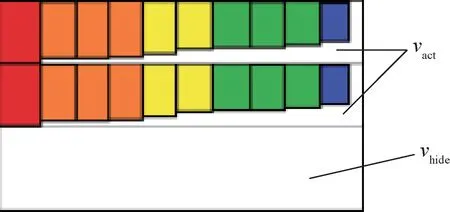
图10 两种浪费体积示意图Fig.10 Schematic diagram of two waste volumes

vact为r中没能完全利用的空间体积之和,即定义体积与实际体积之差。

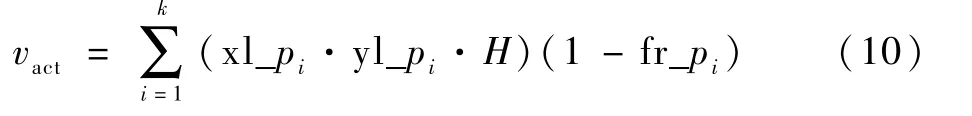
vhide为r中F与S匹配度不足而产生的潜在浪费空间,虽在当层的r中表现不直观,却深刻影响着整体利用率的高低。

计算方式如下:对r模拟新一轮的复合层生成,选取生成的4 种复合层中实际浪费体积最小者作为潜在浪费体积。

最终选择vact与vhide之和vwaste最小的n个r作为新一轮四叉树搜索的con。

算法5复合条生成算法。

算法包括算法5a 和算法5b。

算法5a 设定的复合条最低利用率略高于算法5b,将不满足算法5a 行李放入算法5b 重新生成s。目的为生成更多的s以在搜索过程中增添更多组合,如图11 所示。实验证明,同时使用算法5a 和算法5b 比单一使用算法5a 效果更好。

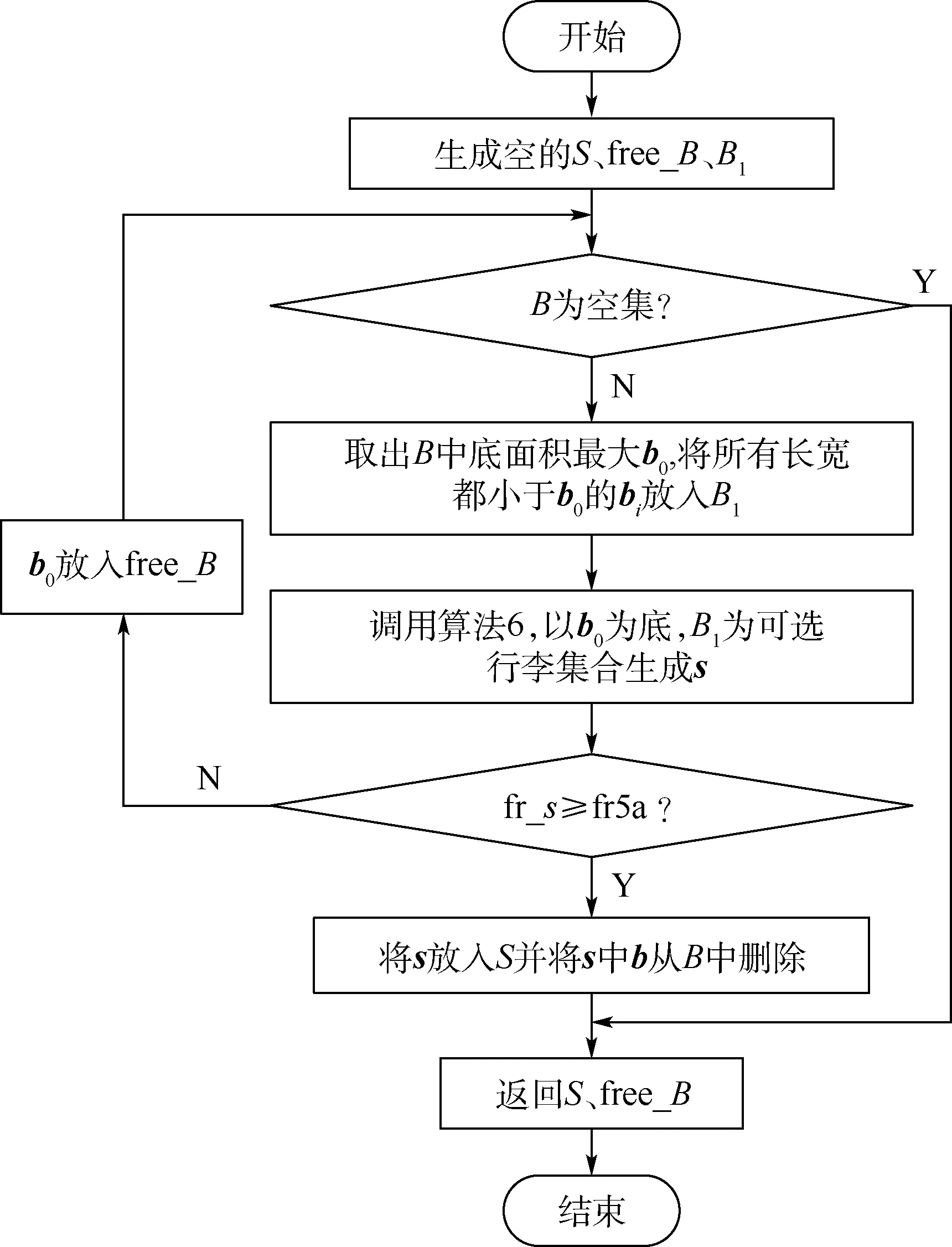
图11 算法5a 流程Fig.11 Flow chart of algorithm 5a

复合条生成算法2 与算法5a 流程相同,使用free_B代替B为总的行李集合。

算法6动态规划算法。

利用动态规划算法解决一维背包问题的原理,在生成复合条时将b0以上行李体积视为物品价值,高度视为物品质量,将高度H视为背包容量。用于复合层生成时与此同理,不再赘述。

3 计算实验

动态四叉树搜索算法实现了最终码放方案可视化,并使用ABB 公司IRB6700 型号机械手实现现实环境验证。算例验证数据选取原则如下:行李车数据选取国内民航机场常规行李车尺寸,为260 cm ×135 cm ×80 cm;参照国内单航班行李处理情况,确定同一航班下70 个不同尺寸的行李箱为码放方案输入,各尺寸所占比例的设定依据为国内某枢纽机场自助行李托运设备信息采集系统导出的历史尺寸数据统计分布。其中,行李箱尺寸型号判定依据为其三边之和(如24 寸行李箱定义为三边之和不超过136 cm,将三边之和范围在128 ～136 cm 之间的行李箱划分为24 寸行李箱,1 寸=0.033 m),具体划分比例如表1 所示,行李数量及各尺寸型号所占比例能够在某种程度上代表机场行李车码放输入的常态。由于存在同尺寸行李箱的三边长度也并不完全一致的情况,表1 给出的是各行李箱尺寸范围。考虑到现实码放环境中存在做工误差、检测误差及行李膨胀等影响行李箱尺寸的因素,因此,为行李箱尺寸添加随机数以反映以上因素对行李箱尺寸的影响。重复30 次实验以验证本文算法稳定性。随机数区间如下:长度为[ -1,1]cm,宽度为[ -1,1]cm,高度为[ -1,3]cm。

表1 航空行李实验数据Table 1 Experimental data of air luggage

3.1 算法对比测试

选取满足同样现实约束的算法对以上测试算例开展比较验证实验,文献[17]的算法可满足同样的严格现实约束,故选取其中的HOBTS 算法与本文DQS 算法进行对比。

经多次实验,DQS 算法中各项参数修正后设定如表2 所示。完成30 次码放后,DQS 算法和HOBTS 算法的空间利用率如图12 所示,其各项统计参数如表3 所示,其中4 次码放方案结果如图13 所示。

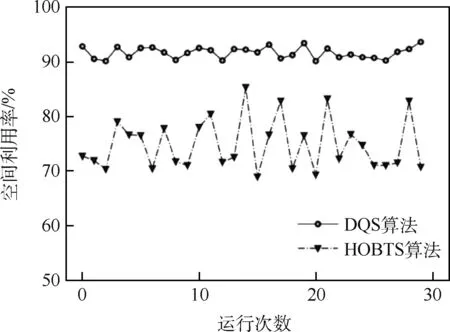
图12 DQS 算法与HOBTS 算法结果对比Fig.12 Comparison of results between DQS and HOBTS algorithms

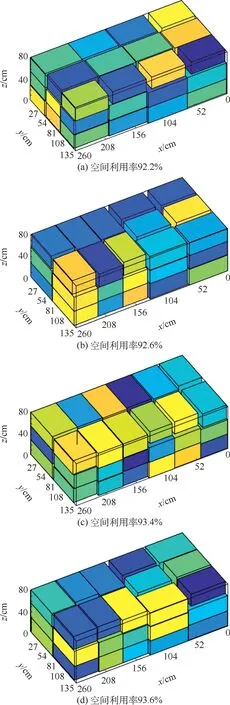
图13 DQS 算法码放的4 个结果Fig.13 Four results of DQS algorithm stacking

表2 DQS 算法参数Table 2 Parameters in DQS algorithm

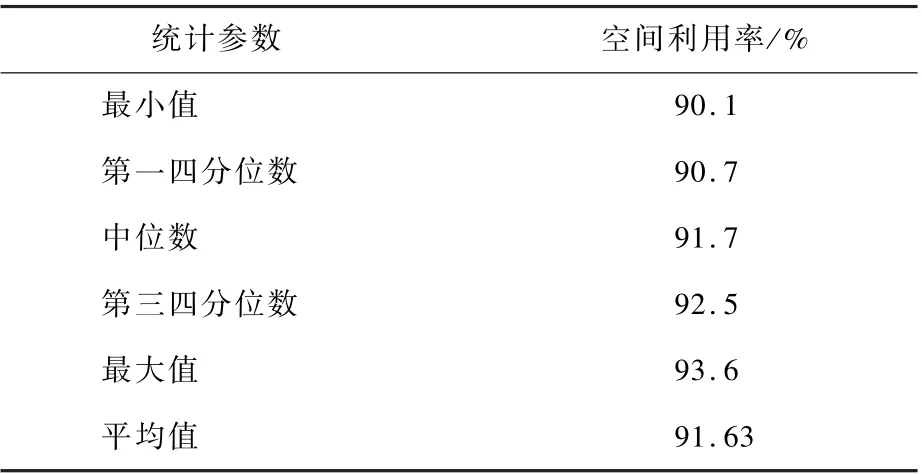
表3 DQS 算法30 次运算结果Table 3 30 operation results in DQS algorithm

使用HOBTS 算法完成30 次标准民航行李车码放后得到的空间利用率如图12 所示,其各项统计参数如表4 所示,其中4 次码放方案结果如图14所示。

图14 HOBTS 算法码放的4 个结果Fig.14 Four results of HOBTS algorithm stacking

3.2 算法对比分析

结合图12 与表3、表4 对比分析可知,DQS算法在本文算例中生成的码放结果平均空间利用率为91.63%,高出HOBTS 算法16.83%,相比于目前仅50%空间利用率的人工码放方案也表现出了足够的优秀性。比人工码放高的空间利用率是机场行李码放自动化与智能化的保障,利用率越高,处理相同数目的行李箱时使用的行李车数量越少,为机场节省更多的行李车资源,提升机场资源利用率和效益。在算法稳定性的表现上,从四分位数来看DQS 算法的实验结果更为集中,因随机数添加所导致的结果波动更小,0.010 557 的利用率标准差低于HOBTS 算法的0.046 709,算法稳定性更好。现实码放往往存在多种扰动使得算法无法发挥出应有的性能,优秀的算法稳定性可以使算法更好地适应复杂的现实码放环境,从而降低扰动对算法的负面影响。

表4 HOBTS 算法30 次运算结果Table 4 30 operations results of HOBTS algorithm

DQS 算法最大的优势在于:有针对性地根据民航行李车的码放环境设计了算法,实现了对剩余空间更大化的利用,优化了树搜索中局部最优的弊端。具体而言,在行李车码放的环境中,单个行李的体积相对于整个行李车占比较大,能够放入行李车的行李较少。因此,剩余空间能否被更有效的利用是决定整体利用率的关键之处。而大多数启发式装箱算法的结果是通过将多个码放序列循环演化后选取最优者而得到的,演化过程往往是以随机改变序列中的值代表的随机性和根据算法中自带的演化公式生成新序列代表的方向性相结合,而演化公式的意义往往与装箱问题无关,并非是根据箱子剩余空间设计的公式,因此演化过程存在一定的盲目性,最终得到的最优解一定程度上是因为产生了足够多不同的序列,得到了较好的结果。而DQS 码放序列的生成是基于剩余空间的,在码放过程中动态地分析剩余空间,并根据剩余空间与尚未码放的行李箱匹配程度确定了当下的序列内容,每完成一次码放重新分析一次,因此当完成码放后的剩余空间对整体影响较大时,DQS 算法优势明显。以HOBTS 算法为例,其在三维装箱算法的标准测试集中表现优秀,可以达到90%的空间利用率,然而在本文测试中只有75%的空间利用率。主要原因在于:标准测试集中箱子体积相对于整个容器较小,一个容器中可装入约100 个箱子;码放完成后无法继续码放的空间相对较小,剩余空间对整体的空间利用率影响很小。而在行李车的环境中,行李箱体积相对较大,行李车只能装入约30 个行李箱且只能正放,完成码放后无法继续码放的剩余空间对整体空间利用率的影响极大,即使剩余空间中多码放一组行李也将极大地提高整体利用率。因此,标准测试集中结果与本文测试算例所得结果不具有相比性。

DQS 算法相对于HOBTS 算法在本文算例中的优势及提升具体值分析如下:

1) 设计了动态选择算法。 DQS 算法在码放时,考虑了已码放结果和未码放空间双重因素,既考虑了完成码放部分的空间利用率,还考虑了剩余未码放空间中是否仍能继续保持高利用率码放,从整体的角度选择码放方案。基于此,DQS算法所得方案剩余空间小于HOBTS 算法,DQS方案大多码放复合条为12 组,而HOBTS 方案大多为10、11 组,如图13、图14 所示。以算例中最多的24、26 寸箱子计算可得,动态选择算法可提升7.5% ～18.0%的空间利用率。

2) 设计了动态的最低空间利用率公式。DQS 算法在复合层的生成中可以根据剩余空间改变最低空间利用率,使得生成的复合层总体空间利用率更高且更均衡,提升空间利用率。 DQS算法中复合层空间利用率平均约为95%,HOBTS算法中空间利用率为91%,可提升约4%。

将图13(b)的码放方案在现实环境中码放实验,结果如图15 所示。可见,在民航行李车中码放行李的表现上,DQS 算法是有效的。

图15 现实码放结果Fig.15 Real-world stack result

3.3 多样性数据实验与分析

为进一步验证DQS 算法的稳定性与实用性,将其应用于更多样化的行李箱数据集合,以异构程度划分,运算结果如表5 所示。将DQS 算法应用于三维装箱算法的标准测试集BR1 ～BR7,并与其他约束相近算法做对比进一步验证DQS 算法的适应性,码放结果如表6 所示。

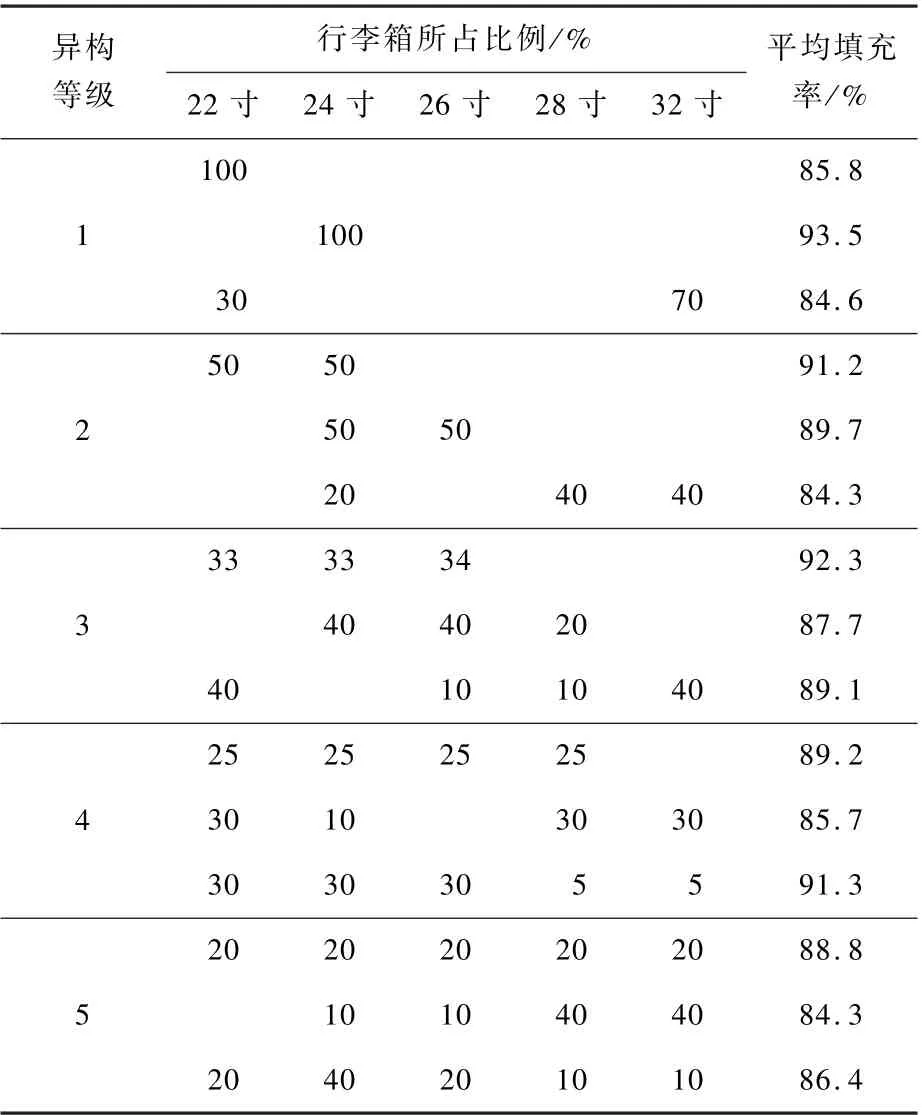
表5 多样性数据集运算结果Table 5 Operation results of diverse dataset

由表5 可得,同异构等级下,随着数据集中大尺寸行李箱的加入,平均填充率有所降低,如异构等级2 数据集中,当28、32 寸行李占比较大时,填充率显著降低,因此该算法对中小尺寸行李箱(22、24 寸行李箱)的码放更具优势;随着数据集异构性的增强,平均填充率并未降低。而当大型号行李箱的数量较少时,平均填充率反而有所提高,如异构等级4 的第3 组平均填充率为91.3%,该数据集大尺寸行李箱较少,平均填充率高于异构等级1、2、3 中大部分同样大尺寸行李箱较少的数据集。因此,该算法对较强异构的行李集合码放更具优势。经分析原因在于:小尺寸行李箱可被该算法中的“填缝算法”更好的利用,较强异构的行李集合可以生成更多的组合供该算法中“动态选择算法”加以选择,因此,DQS 算法更适合中小尺寸强异构性的行李集合码放。根据多样性数据集实验结果可得,算法的平均填充率保持在84.3% ～93.5%,算法稳定性较好。

DQS 算法在三维装箱标准测试集中与其他算法的结果对比如表6 所示。箱子种类数分别为3、5、8、10、12、15、20,异构性由弱到强,其他算法结果均是在满足C1 与C2 约束条件下所得,DQS算法满足C1、C2、C3 约束。在多出的C3 与民航行李箱自身只允许正放的严格约束下,DQS 算法表现与其他算法相差不大,甚至在BR2 测试集的结果中以95. 1% 的填充率高于所有其他算法。然而,由于DQS 算法的约束更严格,在除BR2 的其他测试集下结果仍小于大部分其他算法。但随着测试集异构性的增强,差距也在不断缩小,最终在BR6 中以92. 8% 的填充率超过了HSA 算法(92.7%),在BR7 中以92. 2% 的填充率超过了HAS 算法(92.0%),印证了上文由多样性数据集得出的DQS 算法对强异构集合更为适应的结论。