基于复杂网络理论的电力网络抗毁性分析

郭明健，高 岩

(上海理工大学系统科学系，上海 200093)

0 引言

电能是现代社会中最重要、最方便的能源。发电厂将其它形式的能量转换成电能，电能经过变压器和不同电压等级的输电线路输送并分配给用户，再通过各种用电设备转换成用户需要的能量。生产、输送、分配和消费电能的各种电气设备连接在一起而组成的整体称为电力系统。现代电力系统是一个复杂系统，随着其规模的不断扩大，维持电网稳定难度不断提升[1-3]。近些年，国内外发生了多起大型停电事故，例如2019年美国纽约城区因某变电站老旧变压器起火，导致整个城区大型停电事故发生；2017年中国台湾因工作人员疏忽，致使供气中断导致电厂跳机，进而发生全台大断电事故。这些停电事故会给社会经济和人民生活带来长期的不利影响。近年来，人们对于智能电网的需求侧响应[4]及系统能源管理[5]的研究已经逐步完善，然而对于其安全性及稳定性的研究还不够成熟。因此电力系统的抗毁性分析不仅具有理论研究意义，更具有保证电网安全稳定的现实价值。

网络抗毁性是指遭受随机性或确定性攻击时，网络保持其连通性的能力。网络抗毁性可分为静态抗毁性和动态抗毁性[6-7]，其区别在于故障节点或边是否会导致其他节点或边的故障。抗毁性分析是电力系统中识别易受攻击的脆弱组件的关键问题。

由于电力系统的复杂性，基于电气介数的度量方法难以系统分析故障的传播过程，复杂网络理论利用网络拓扑结构及属性可有效分析电力系统抗毁性。复杂网络理论源于图论的研究，随着其理论发展，现已广泛应用于社交网络[8]、生物科学[9]、电力系统[10]等领域。对于电力系统的抗毁性分析，构建拓扑脆弱性指数是一种流行的评估网络脆弱性的方法，文献[11]基于拓扑度量来分析电力系统网络，例如平均最短路径长度，出入度等参数。然而这类方法不能揭示失效节点的传播机制，文献[12]基于故障链的级联故障图提出一种评估输电网络抗毁性的方法；Thams等[13]基于凸优化及复杂网络提出一种模块化和高度可扩展的算法以便进行安全性评估；文献[14]基于介数中心性采用蓄意攻击得到边的抗毁性参数识别关键设施。

本文首先基于复杂网络理论，将变电站、发电厂等站点看作节点，将传输电缆看作边构建电力网络拓扑图；接着模拟针对该网络的随机攻击和蓄意攻击，并提出网络效率变化率作为抗毁性分析的评估参数；最后以上海市崇明区电力网络做实例分析，进而针对性地提出解决方案，以确保电网安全稳定运行。

1 模型构建

相较于其他工业系统，电力系统最大的特点是不易存储，即其生产、输送和消费在同一时刻实现。电力系统的基本要求是保证安全优质地向用户供电，但风电、新能源汽车、光伏、特高压等新能源也将给新型电力系统稳定运行带来巨大挑战[15]。新型电力系统结构示意图如图1所示。

图1 新型电力系统的结构示意图Fig.1 Schematic diagram of the structure of the new power system

新型电力系统中稳定运行受到光伏或风电发电量的影响，光电风电功率不确定性高、抗扰性弱，易造成电力系统常规机组切除[16]，极大约束了电力系统对新能源的消纳水平。其主体结构包含发电厂、变电站、输配电线路。为了便于研究，在构建电力网络模型时进行如下简化：1)不考虑功率、频率、电压、电流、磁链、电动势等动态参数的影响；2)不考虑输入输出设备差异，将任一发电厂、变电站视为相同类型的节点；3)不考虑输电配电线路的差异，将节点间的连接视为相同的边。

基于前文将电力系统看作一个网络，将不同类型的变电站、发电厂等站点看作同类节点，将输配电线路看作边构建电力拓扑网络。电力网络拓扑图表示为G=(N,E)，其中集合N包含节点，即变电站、发电厂等站点；E表示网络的边集合，代表节点间的传输电缆。此外，其邻接矩阵为A={aij}。其中aij=1时表示节点i与节点j相连接，aij=0时两节点不相连，该模型的加权邻接矩阵B={bij}且定义为

(1)

其中，ωij为节点i与节点j边上的权值，为了简化网络，均以1带入计算。

2 参数选取和评估指标选取

2.1 参数选取

研究网络抗毁性时，首先要确定枢纽节点，其中介数中心性、接近中心性反映节点重要程度的指标。介数是使用最广泛的中心性指标，当网络中移除具有较大介数中心性的点或边时，会使得网络处于高中断的风险中[17]。节点的接近中心性反映某一节点与其他节点之间的接近程度，用一个节点到所有其他节点的最短距离的平均值的倒数来表示接近中心性，该节点距离其他节点越近，它的接近性中心性越大，它也可以有效反映基于时间序列产生的递归网络之间的紧密程度[18]。本文将介数中心性和接近中心性作为判断节点重要程度的参数。

节点介数是指一个网络里通过节点的最短路径条数，节点i的介数中心性可表示为

(2)

节点i的接近中心性可表示为

(3)

其中，di为节点i到其余各点的平均距离，平均距离的倒数就是接近中心度。

2.2 评估指标选取

评估网络的抗毁性，即评估重要节点遭遇攻击后网络的连通性[19]。网络在受到攻击时，其连通性越高崩溃概率就越小，因此网络连通性是衡量网络崩溃程度的重要指标。网络的连通性主要体现在故障点数量[20]、连通子图数量[20]、最大连通子图的比率[20]以及网络连接效率上，故选用它们作为评估指标。其中故障点数量，即为网络受到攻击后，失效节点的数量。连通子图数量是指节点遭受攻击失效后划分为不同连通子图的数量。网络遭受攻击致部分节点失效后，完整网络被分割成多个互不联系的子网，其中弧边连接数及节点数最多的子网为最大连通子图，最大连通子图的节点数N0与原网络节点数N的比值定义为最大连通子图的比率LCC。LCC越大，该网络遭受攻击时被破坏的程度越低。

(4)

网络传输效率可以用网络连接效率衡量，即网络效率，节点i和节点j之间的网络效率为

(5)

其中，dij为节点i和节点j之间的最短距离。

整个网络的连通效率定义为所有节点的平均网络效率，即

(6)

网络在遭受攻击致部分节点失效后，网络效率也会变化，本文提出网络效率变化率μE作为评估指标。假设被攻击前网络效率为E0，攻击后网络效率为E′，攻击前后节点数变化为Δn。将攻击前后的网络效率变化与节点数量的变化的比值定义为网络效率变化率μE。μE越大表示其节点重要性越高，其表达式为

(7)

3 电力网络的攻击方法

通常研究抗毁性时会采用两种攻击模式，分别为随机攻击和蓄意攻击。随机攻击是对网络中的节点或边进行一定概率的随机攻击和破坏。通常展现为非人为故意破坏造成的故障，例如硬件故障以及自然灾害造成的传输设备损坏，属于随机攻击。蓄意攻击是指对网络的进攻是按照策略进行的。若网络连接中起关键作用的节点或边被人为破坏，此时攻击方已获知点与边的信息，清楚地知道网络中的重要节点和边，并按照亟定顺序攻击节点或边。根据静态参数的不同选用两种蓄意攻击策略：网络节点度优先攻击策略和实时接近中心性攻击策略。

网络节点度优先攻击策略的攻击过程：1)计算网络中所有节点的度，按照其节点度将所有节点排序；2)找到度最大的节点并从网络中删除，攻击过程中计算网络效率；3)按照1)中的排序依次攻击，直至所有节点删除。

实时接近中心性攻击策略的攻击过程：1)计算网络中所有节点的接近中心性参数；2)找到接近中心性最大的节点，并对其发起攻击使其失效；3)重新计算剩余节点的接近中心性；4)重复2)和3)，直至所有节点失效。

在现有的基于介数中心性攻击策略[20]的研究基础上，本文提出实时攻击的方式，即移除最高接近中心性的节点后重新计算剩余网络的接近中心性，循环直至网络中所有节点被删除的攻击方式。采用实时接近中心性攻击方式时，给予网络反应的时间更短，攻击更具有侵略性。相较节点度优先攻击策略，实时接近中心性的策略更具有实时性，且接近中心性也更能反映节点的重要程度。

4 实证分析

实证分析以上海市崇明区为例，因为：1)崇明区包含着工厂，商场及农场住等不同的设施，整个系统的负荷多元化；2)崇明区具备风能、太阳能、生物质能、潮汐能、地热能等5种可再生能源，种类多，且可再生能源装机容量占最高负荷的比重超过48%。随着技术及机制创新，崇明区将打造成风光储一体、农光互补和能源互联网的集成示范，针对它的研究具有前瞻性；3)崇明区电力网络规模适中且具有典型性。以往对于电力系统抗毁性分析的文章缺少现实数据，我们根据崇明区2021年电网地理接线图构建电力网络拓扑图如图2所示，网络含有63个节点及88条边。图2中的变电站，发电厂等站点均以英文缩写形式表示，英文字母的大小代表站点度的大小，且站点布局与现实布局不关联。接下来基于Python软件进行了随机攻击和蓄意攻击的仿真实验，研究图2所示拓扑图，得到仿真结果。

通过复杂网络参数可知图2的网路效率为0.331 8，连通子图数为1，最大连通子图比率为100%。通过随机攻击实验和蓄意攻击实验分析传输网络的抗毁性。由于蓄意攻击时，攻击方很难获取边的准确位置，因此仅采用攻击节点的攻击方式，本文蓄意攻击包括网络节点度优先攻击和实时接近中心性攻击两种策略。

4.1 随机攻击仿真结果

在电力网络遭受随机攻击时，都会使得站点无法正常工作，此类状况一般不会导致多个节点同时失效。采用逐一随机攻击的方式，网络效率以及最大连通子图数量同被攻击节点数的关系分别如图3和图4所示。图3中纵坐标前后分别代表攻击站点和网络效率变化率，通过分析网络效率变化率，进而判断节点在网络中的重要性。

图2 上海市崇明区电力网络拓扑图Fig.2 Topological diagram of power transmission network in Chongming District of Shanghai

图3 随机攻击策略网络效率图Fig.3 Network efficiency graph under random attack strategy

图4 随机攻击策略最大连通子图变化Fig.4 Connected subgraphs under random attack strategy

网络被随机攻击后变化程度如图3、图4及表1所示。由图3、图4和表1可知节点CXZ(长兴站)，BB(堡北)，CZJ(陈家镇)，TJZ(团结站)，ZSG(中双港)，CJZ(长江站)在遭受攻击后对整个网络的联通影响较大，即该类节点为枢纽节点，需要加强保护。

表1 随机攻击下枢纽节点网络效率变化率Tab.1 Network efficiency of hub nodes under random attack

4.2 蓄意攻击仿真结果

采用节点度优先攻击策略和实时接近中心性优先攻击策略对网络展开蓄意攻击，分别按照制定的策略选择22个点对网络采取攻击，其中实时接近中心性优先攻击策略是作者根据前人[20]的研究改进提出的一种蓄意攻击的策略。相对于随机攻击的偶然性，蓄意攻击类似于黑客攻击，具有针对性及破坏性。通过比较网络的变化程度得出网络的重要节点及变化规律，实验仿真结果如图5及图6所示。

由图5和图6可知崇明区电力网络遭遇数次攻击后，两种策略下前三次攻击后网络连通效率下降较多，由此可见做好前期应对并及时处理在保护电网中作用巨大。对比两图，采用节点度优先攻击策略且网络受到17次攻击以后，网络效率下降到0.06%，失效点数目为38，整个网络几乎处于瘫痪状态;当采用实时接近中心性优先攻击策略时，遭受到15次攻击后，网络效率下降至0.57%，失效点数目为34，连通子图数量为19，此时网络已瘫痪。不难发现网络效率变化速率越大，整个网络的连通性受到的影响就会越大，网络遭到的破坏性也就越大。

图5 节点度优先攻击策略网络效率图Fig.5 Network efficiency graph under node degree priority attack strategy

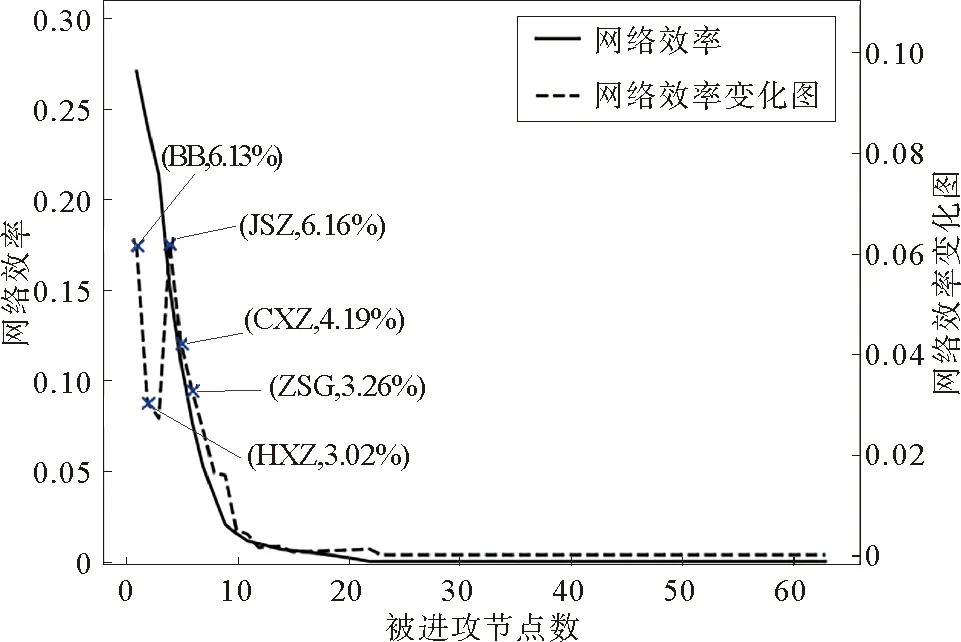
图6 实时接近中心性优先攻击策略网络效率图Fig.6 Network efficiency graph under real time centrality closeness priority attack strategy

将实验现象同文献[11]及文献[13]中的方法进行比较，可以得出以下几点规律：

1)无论是采用文献[11]中故障链的级联故障图，还是采用文献[13]中同时进行节点攻击及边攻击，或是实时接近中心性优先攻击策略时，针对枢纽节点的攻击会导致网络中60%以上节点失效，崩溃程度大。

2)文献[11]中仅选用节点的出入度作为判断枢纽节点依据，依此选中的枢纽节点在遭到攻击后，网络效率下降速率几乎没有变化，无法有效判断枢纽节点的重要程度。文献[13]中选用节点的介数中心性同边的介数中心性的乘积作为判断枢纽节点的依据，但它没有实时计算变化后的节点和边的介数中心性值，其网络效率变化较快，无法实时判断其余枢纽节点。相较而言，文中实时接近中心性优先攻击策略既可快速识别枢纽节点，又能根据网络效率变化率判断枢纽节点的重要程度。

4.3 结论

崇明区志在建设世界级生态岛，岛上电能供给多元化，包含有火力发电，风力发电以及光伏发电。崇明区电力系统的负荷多元化，其电力网络具有大型城市的多样性。因此对于该区电力网络的抗毁性分析具有典型性及普适性。根据模拟攻击电力网络的结果，可总结出几点结论：1)根据随机攻击下网络效率的变化，可知电力网络中某些节点失效后对于网络效率的影响远高于其他节点，这类节点属于中心节点；2)在蓄意攻击策略下，电力网络的抗毁性很差，前几次攻击会导致网络效率急剧下降；3)网络效率变化率丰富了抗毁性分析指标，当网络遭受攻击可反馈防护效果，蓄意攻击的仿真结果并进一步验证其有效性。

根据前文总结的实例电力网络的特点，考虑中心节点的重要程度，本文基于实时接近中心性攻击策略提出一种分段式保护方案，从而有效保护重要节点，具体步骤为：1)计算求得网络中所有节点的接近中心性；2)根据接近中心性大小排序，按照10%，20%，70%的比例将节点分成3档，分段式保护节点；接近中心性前10%的节点采用最高阶保护措施，前10%～前30%的节点采用次级保护措施，排序靠后的70%采用基础保护措施；3)当网络遭受攻击，结构发生变化时，重复上述两个步骤。

其中分段式保护节点的各分段具体措施为：1)基础保护：采用定时监测，失效后即刻维修；2)次级保护：采用实时监测，失效后即刻维修；3)最高阶保护：采用实时监测，若检测部分失效启用备用设备，最快速度恢复其工作。

受到最高阶保护的节点是攻击策略优先攻击的节点，使用分段式保护可以有效保障大多数电力网络安全稳定运行。

5 结语

抗毁性分析对于提高电力网络的鲁棒性有着重要作用，文中选用崇明区为实证对象，对于该区电力网络的研究成果具有典型性及前瞻性。本文通过应用复杂网络理论找出中心节点，针对性提出更具破坏性的策略，并模拟电力系统现实中遭受攻击的情况从而进行网络抗毁性分析，最终建设性提出分段式保护方案。对保障电网安全、降低大规模停电事故发生概率具有重要意义。