跨层穿梭车双提升机系统多目标问题优化
2023-01-11李军涛胡启贤刘朋飞郭文文
李军涛,胡启贤,刘朋飞,郭文文
(上海海洋大学工程学院,上海 201306)
0 引言
近年,随着电商物流的快速发展,密集型仓储系统受到众多复杂性因素制约,如:订单的小批量多批次的特性、仓储系统的能耗、车辆的调度、市场上的竞争者所身处的市场经济和社会政治形势环境等。密集型仓储系统变得越来越复杂,使用自动化传统的立体仓库无法高效地解决密集型仓储系统中遇到的各种问题。跨层穿梭车双提升机系统[1]是近年来出现的一种新型智能密集型存储立体仓库。相比于每层一辆车的多层穿梭车系统,跨层穿梭车可以通过换层提升机到其他层进行入库,从而减少穿梭车的数量,具有更高的柔性和鲁棒性。同时政府对能耗也提出了更高的要求,在确保订单快速、准确入库的同时也需兼顾系统的能耗。
目前,国内外学者对于穿梭车系统调度问题进行了研究。Kuo等[2]以时间最小为目标对多层穿梭车进行了研究,并针对系统中车辆和提升机等待时间的问题,提出了M/G/V和M/G/L排队模型。Roy等[3]提出了一种半开环排队网络,以研究机架配置、区域资源分配和车辆分配规则的影响。Yang等[4]从分析模型的角度验证了共享存储下运行模式的优越性,提出了一种求解大型问题的变邻域搜索算法,研究了不同参数对计算效率的影响。Zou等[5]构造了一个fork-join排队网络来研究穿梭车系统的并行处理策略的性能。Carlo等[6]对同一轨道的双提升机系统进行研究,以最短出入库时间为目标函数建立模型,确定了提升机的工作顺序。牟善栋[7]对多层穿梭车系统进行了研究,以出库时间最短建立模型,通过非支配遗传算法对模型进行了求解。王珊珊[8]对由单提升机和单穿梭车组成的跨层穿梭车系统进行研究,以出入库总时间最小建立路径优化模型,并使用改进的离散粒子群优化算法对其求解。于巧玉等[9]为降低任务超时率,将任务出库期限引入穿梭车系统任务调度模型中,使用双层智能优化算法对模型进行求解。国内外对跨层穿梭车双提升系统的相关文献较少,且研究多是以系统作业时间最短为优化目标,缺乏对其他因素的考虑,对跨层穿梭车双提升机系统调度有着一定的局限性。
对于调度中能耗的问题,韩星[10]通过分析穿梭车和提升机运动时的能耗,建立了穿梭车和提升机的速度和加速度的优化模型。Banu等[11]开发了一个基于穿梭车模型的分析工具,可以估计提升机和穿梭车时间的平均值和方差,以及预测每笔交易的平均能耗和能量再生量。Habibi等[12]针对双梭式穿梭车调度问题,构造穿梭车总成本和能耗目标模型,并提出一种改进的双层协同进化优化算法(MCoBRA)进行求解。敏感性分析表明在上层考虑基于类的存储策略对整个目标函数有显著影响。Liu等[13]考虑到能耗问题,建立了双指令周期的交叉穿梭车立体仓库系统模型,并对其最大吞吐量、行程时间和能量消耗进行了估算,分析了吞吐量与能耗的关系。刘紫薇[14]以出库作业时的能耗为目标建立多层穿梭车调度模型,利用改进粒子群算法对模型进行求解。在穿梭车能耗问题上,国内外多以能耗单目标建立模型,未能同时考虑作业时间,影响系统作业效率。
跨层穿梭车双提升机调度问题属于NP-hard问题[15]。国内外对于穿梭车系统同时考虑综合能耗与时间的相关文献较少,将能耗目标引入跨层穿梭车双提升机系统调度中,建立时间与能耗双目标最优的作业模型,运用自适应遗传模拟退火算法对该模型求解,通过对比实验,证明了模型和算法的有效性。
1 跨层穿梭车双提升机仓储系统建模
1.1 问题描述
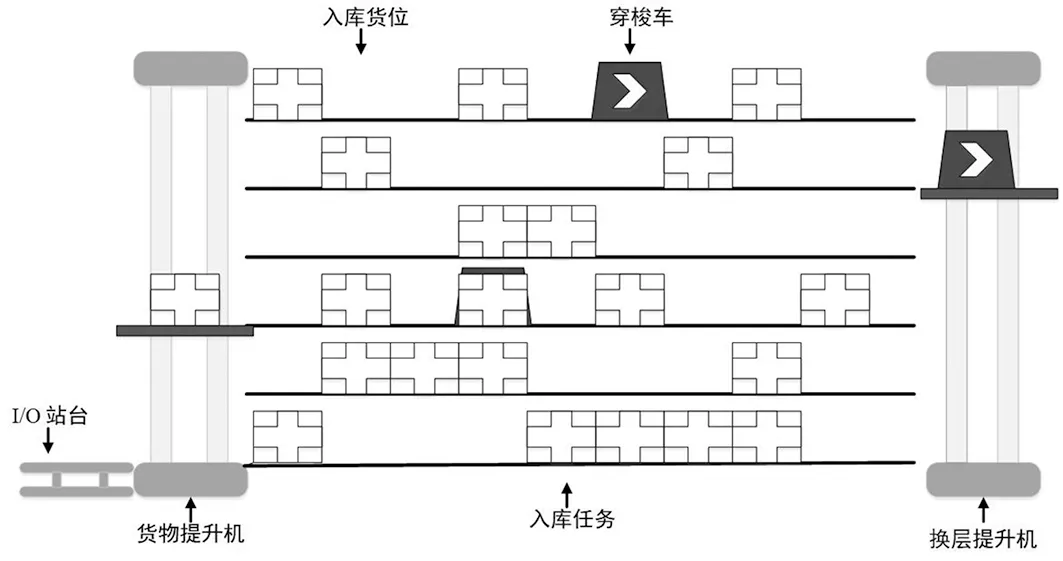
图1 跨层穿梭车双提升机系统货架立面图Fig.1 Shelf elevation of tier-to-tier multi-shuttle warehouse system with double lifts
跨层穿梭车双提升机系统由货架、直线穿梭车、货物提升机、换层提升机、辊道等组成。其中直线穿梭车在货架上水平移动,负责货物的搬运和存取。货物提升机和换层提升机位于巷道的两端,分别负责货物的垂直运动和穿梭车的换层运动[16]。系统立面图如图1所示。
该系统采用穿梭车和提升机协同作业,首先货物提升机将货物从站台送至入库所在层,然后穿梭车将货物送至指定货位,完成一次任务入库。入库流程图如图2所示。
定义1N={(1,s1),(2,s2)…(i,si)…(n,sn)}为入库任务集合,i为入库任务序号,si=(xi,yi)为入库任务i坐标。R={1,2…j…r}为一个巷道中穿梭车的集合,j为穿梭车编号。本文以入库任务排序为例,研究跨层穿梭车双提升机系统任务调度。
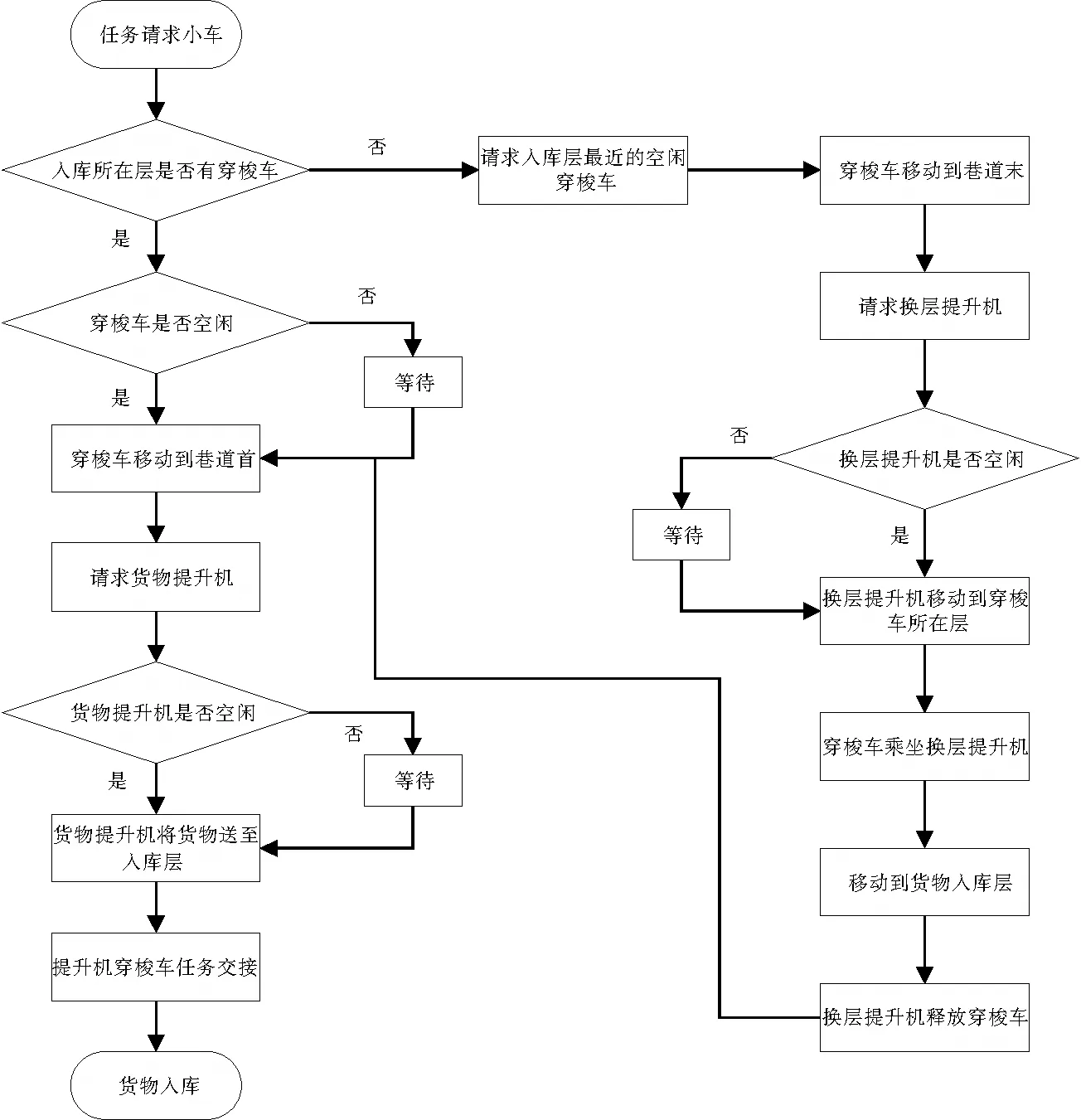
图2 入库流程图Fig.2 Flow chart of storage
条件假设为:1)本研究只考虑一个巷道;2)每个任务只能由一辆穿梭车执行,每个车只能执行一个任务;3)穿梭车的初始位置在巷道首端,提升机初始位置在货架最底层;4)任务请求小车的时刻为任务到达I/O处,即前一任务乘坐货物提升机的时刻;5)入库所在层没有穿梭车时,优先请求离入库所在层最近的空闲穿梭车,若有多辆穿梭车距离入库所在层最近,则选择编号最小的穿梭车;6)穿梭车移动到巷道首端后,申请货物提升机;穿梭车移动到巷道末端后,申请换层提升机;7)两种提升机的调度遵循FCFS原则——先到先服务原则,若多辆穿梭车同时申请,则优先响应编号最小的穿梭车;8)每层至多有一辆穿梭车,以免发生碰撞和死锁;9)不考虑货物的重量对速度和加速度的影响。
1.2 作业时间分析
1.2.1 入库作业流程分析
考虑到穿梭车初始位置与入库货位可能不在同一层,可以根据入库任务层是否有穿梭车分为跨层入库和不跨层入库两种情况,入库作业示意图如图3,横轴为货架的列,纵轴为货架的层。


图3 入库作业示意图Fig.3 Schematic diagram of storage
穿梭车j(j=1,2,…,r)执行任务i(i=1,2,…,n),当yi=yj时,不跨层入库,需要经过3个节点变化:
1)穿梭车j由穿梭车所在位置节点移动至入库层巷道首端节点,时间为tstj:
(1)
2)货物提升机由I/O节点移动至入库层巷道首端节点,时间为sti:
(2)
3)穿梭车j由入库层巷道首端节点移动至入库货位节点,时间为reti:
(3)
穿梭车j执行任务i不跨层入库时所用时间为Dtij:
Dtij=tstj+sti+swtij+reti+2srt
(4)
其中,swtij为穿梭车j执行任务i等待货物提升机响应的时间。srt为穿梭车取/放货物的时间。
当yi≠yj时,需要经过6个节点变化:
1)穿梭车j由穿梭车所在位置节点移动至巷道末端节点,时间为tctj:
(5)
2)换层提升机由上次换层节点移动至穿梭车j所在层节点,时间为wtjk:
(6)
3)换层提升机由穿梭车j所在层巷道末端节点移动至入库层巷道末端节点,时间为ctij:
(7)
4)穿梭车j由巷道末端节点移动至巷道首端节点;为固定时间tH:
(8)
5)货物提升机由I/O节点移动至入库层巷道首端节点,时间为sti。
6)穿梭车j由入库层巷道首端节点移动至入库货位节点,时间为reti。
穿梭车j执行任务i跨层入库时所用时间为Ctijk:
Ctijk=tctj+cwtij+wtjk+ctij+2set+tH+sti+reti+2srt
(9)
其中,cwtij为穿梭车j执行任务i等待换层提升机响应的时间,set为换层提升机装载或者卸载穿梭车的时间。
根据穿梭车跨层入库和不跨层入库两种作业方式,建立穿梭车j完成入库任务所需时间的数学模型Tj:
(10)
其中,
θij={0,1}i=1,2,3…,n;j=1,2,3,…,r
(11)
δij={0,1}i=1,2,3…,n;j=1,2,3,…,r
(12)
公式(10)中θij和δij为决策变量,当穿梭车j执行任务i时,θij为1,否则为0;当穿梭车j执行任务i需跨层时δij为1,否则为0。

图4 穿梭车和提升机的配合作业图Fig.4 Working diagram of shuttle and lift
在跨层穿梭车双提升机系统中,穿梭车为并行作业模型,因此整个任务的入库时间为完成时间最大的穿梭车的工作时间。建立入库总时间模型:
F(t)=max(Tj)
(13)
1.2.2 等待时间分析
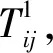
提升机调度服从FCFS原则,当穿梭车申请提升机时,如果提升机的上一个任务未完成,则穿梭车需等待提升机响应。根据提升机类型不同,可以将穿梭车j(j=1,2,…,r)执行任务i(i=2,3,…,n)等待的时间分为等待货物提升机的时间swtij和等待换层提升机的时间cwtij:
(14)
(15)
1.3 能耗分析
1.3.1 穿梭车能耗
当穿梭车加速运动时,牵引力和功率分别为Ft和Pt:
Ft=mgCr+maxfr
(16)
(17)
当穿梭车减速运动时,牵引力和功率分别为Fb和Pb:
Fb=maxfr-mgCr
(18)
(19)
当穿梭车匀速运动时牵引力和功率分别为Fc和Pc:
Fc=mgCr
(20)
(21)

根据公式(1)、(3)、(5)、(8)分别可以得出:
由原来位置到巷道首端的能耗tswj为
(22)
由巷道口到货位的能耗rewi为
(23)
由原来位置到巷道末端的能耗tcwj为
(24)
由巷道首端到末端的能耗wH为
wH=t1Pt+t1Pb+(tH-2t1)Pc
(25)
其中,t1为穿梭车由静止到最大速度的时间。
穿梭车j能耗为
(26)
其中,
Dwij=tswj+rewi
(27)
Cwij=tcwj+wH+rewi
(28)
1.3.2 提升机能耗
(29)
(30)
(31)
(32)
(33)
(34)
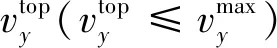
根据公式(2)、(6)、(7)分别可以得出:
货物提升机由I/O节点移动至入库层巷道首端的能耗swi为
(35)
换层提升机由上次换层节点移动至穿梭车j所在层的能耗wwjk为
(36)
换层提升机由穿梭车j所在层节点移动至入库层巷道末端节点的能耗cwij为
(37)
其中,t2为提升机由静止到最大速度的时间。
货物提升机的能耗为
(38)
换层提升机的能耗为
(39)
总能耗模型为
(40)
1.4 目标函数统一量纲
研究采用模糊数学方法对总时间函数F(t)和总能耗函数F(w)去标量化,并根据能耗和时间的重要程度赋予权重,将作业时间和系统能耗双目标模型转化成单目标模型。总目标函数Z为
(41)
约束条件为
(42)
(43)
(44)
其中,φ为权重系数,0≤φ≤1,可根据物流企业对入库效率和节能减排的重视程度对φ取值,若企业追求效率则取较大的权重值φ;反之,若企业追求环保,则取较小的权重。本文根据中国出台的节能减排的政策方针[17],取权重值φ=0.3。
公式(42)表示每个入库任务只能由一辆穿梭车执行,入库任务对应的穿梭车编号唯一。公式(43)表示模型总入库时间不能小于提升机连续工作时间。公式(44)表示在执行跨层入库时,请求换层的时间早于请求货物提升机,且两次申请的时间间隔不得小于换层所用的时间。
2 算法设计
处理NP-hard问题常用的算法有遗传算法、蚁群算法、模拟退火算法等[18]。遗传算法(GA)作为求解优化问题的有效算法,它们是基于“达尔文适者生存理论”推导出来的随机搜索算法,在选择、交叉和变异等生物进化机制的引导下,以自适应的方式探索一个庞大而复杂的搜索空间[19]。遗传算法具有全局搜索能力强,鲁棒性强的特点[20],但也存在算法早熟的缺点。当问题复杂时,还有计算时间长等缺陷。为了弥补遗传算法早熟的缺点,本文将模拟退火算法与自适应遗传算法相结合,设计自适应遗传模拟退火算法,既避免了遗传算法早熟的缺点,又改善了模拟退火算法容易陷入局部最优的弱项。
算法设计规则为:
1)编码:采用自然数编码方式,入库任务编号为编码序号。
2)自适应变异率PMi和自适应交叉率PCi分别为[21]:
(45)
(46)
其中,PMmax为最大变异概率,PMmin为最小变异概率,PCmax为最大交叉概率,PCmin为最小交叉概率,Fi为适应度,Fmax为最大适应度,Fmin为最小适应度,e为一个很小的正实数,防止分母为0。
3)适应度函数:
Fi=1/Zi
(47)

5)跨层穿梭车双提升机调度模型的自适应遗传模拟退火算法步骤:
步骤1:初始化种群和参数;
步骤2:开始迭代。执行选择、变异、交叉操作;
步骤3:计算适应度值,更新并记录最优解;
步骤4:取最优解S1。对当前解进行随机干扰,产生新的解S2,若满足S2 步骤5:判断λ是否小于P,若满足,则替换旧个体且按衰减函数更新温度,否则不替换旧个体,且更新温度; 步骤6:判断是否达到最大迭代次数,若达到输出最优解,否则转到步骤2。 为了验证所提出的模型及求解方法的有效性,本文根据实际中跨层穿梭车系统的性能参数和储存规格,设置了跨层穿梭车双提升机系统的模拟场景,货架层数为12层,每层有40列货格,穿梭车4辆,具体设备运行参数如表1所示。 表1 设备运行参数Tab.1 Operation parameters of equipment 随机生成50个入库任务,入库任务表如表2所示。 根据程序随机得到入库任务的一组序列为:9→26→38→43→34→33→35→40→25→11→18→36→46→29→13→45→27→8→3→22→10→31→5→50→2→19→44→39→7→12→6→24→48→30→1→23→14→28→17→20→37→16→4→27→49→47→42→41→32→15。目标函数值为0.636 5,作业总时间为943.8s,作业总能耗为1 733.5KJ。 表2 入库任务表Tab.2 Storage task table 图5 算法收敛效果比较图Fig.5 Comparison of convergence between two algorithms 通过使用遗传算法和自适应遗传模拟退火算法分别对模型入库作业调度进行对比,来验证算法求解该问题的有效性。遗传算法参数为:种群数量取500,迭代次数1 000,交叉概率PM取0.7,选用部分匹配交叉,变异概率PC取0.1,选用交换变异。优化后所得到的入库任务序列为:44→20→38→42→5→11→35→13→19→40→12→18→48→50→33→2→26→15→8→31→4→29→22→41→3→32→16→43→21→45→24→1→39→25→49→46→27→34→28→9→6→17→37→47→36→7→30→10→14→23。目标函数值为0.351 3,作业总时间为822.7s,作业总能耗为1 520.3KJ。自适应遗传模拟退火算法的参数为:种群数量取500,迭代次数1 000,最大交叉概率PCmax取0.9,最小交叉概率PCmin取0.8,最大变异概率PMmax取0.05,最小变异概率PMmin取0.01,模拟退火的初始温度取2 000℃,终止温度取20 ℃,冷却系数取0.95。优化后所得到的入库任务序列为:6→39→33→47→45→11→26→27→50→46→8→23→10→31→48→3→28→38→35→2→25→21→29→34→32→1→37→15→13→49→40→30→14→24→17→16→5→22→7→41→43→20→18→36→44→19→42→4→9→12。目标函数值为0.218,作业总时间为627.8s,作业总能耗为1 251.4KJ。算法结果如表3所示,算法收敛效果比较图如图5所示。 由表3可知,自适应遗传模拟退火算法比传统的遗传算法求解精度高,对时间和能耗的优化效率也更好。跨层穿梭车入库作业的时间主要优化时间是穿梭车等待货物请求时间,即穿梭车空闲时间,自适应遗传模拟退火算法对穿梭车空闲时间大幅度优化,对穿梭车等待两种提升机时间也有所优化。 从图5中可以看出遗传算法收敛较慢,求解精度差;而本文提出的自适应遗传模拟退火算法,引入了自适应变异率和自适应交叉率,并通过模拟退火对解进行干扰,获得更优的解,相比于遗传算法,其求解收敛快、精度优势较大。故可以证明本文所提出的算法求解该问题的有效性。 为了分析模型中各参数变化对模型的影响,以初始值为基准,令各参数逐渐增加(减少)10%,20%,30%,40%。 通过表4、表5可以看出增加穿梭车或提升机的最大速度,总目标函数变化不大,总时间减少,总能耗增加。其中提升机速度的增加对时间和能耗的影响更为显著。 通过表6、表7可以看出增加穿梭车或提升机的加速度,都会使总时间减少,但随着穿梭车加速度增加,总能耗增加,总目标函数变化不大,而随着提升机加速度增加,总能耗减少,总目标函数也出现变小的趋势。 表4 穿梭车最大速度分析Tab.4 Sensitivity analysis of maximum speed of shuttle 表6 穿梭车加速度分析Tab.6 Sensitivity analysis of acceleration of shuttle 表5 提升机最大速度分析Tab.5 Sensitivity analysis of maximum speed of lift 表7 提升机加速度分析Tab.7 Sensitivity analysis of acceleration of lift 针对跨层穿梭车双提升机系统任务入库问题,分析其作业流程,建立了作业时间和系统能耗的双目标模型。采用自适应遗传模拟退火算法对模型进行求解,实验结果表明,所建立的调度数学模型及自适应遗传模拟退火算法是可行有效的,在一定程度上能够减少作业时间和能耗,提高系统效率,对于企业来说,一方面提高了穿梭车双提升机系统的效率,另一方面又能减少能量消耗,降低成本。同时分析了穿梭车、提升机的速度、加速度与系统时间和能耗之间的关系,改变穿梭车的速度或加速度对总目标函数的影响不大,增加穿梭车的速度或加速度时,会导致总时间减少,总能耗增加。而增加提升机加速时,导致总时间和总能耗都减少,目标函数随之减小。可以通过适当增加提升机加速度来使总时间和总能耗减少。为跨层穿梭车系统的研究和应用提供了借鉴意义。 但本文研究所建立模型仍然具有一定程度局限性,本文只考虑任务排序,未考虑给穿梭车分配任务,导致会出现穿梭车效率差距过大,部分穿梭车闲置时间过长等问题,未来将对穿梭车任务分配进行研究。3 算例分析

3.1 算法有效性验证


3.2 参数灵敏度分析
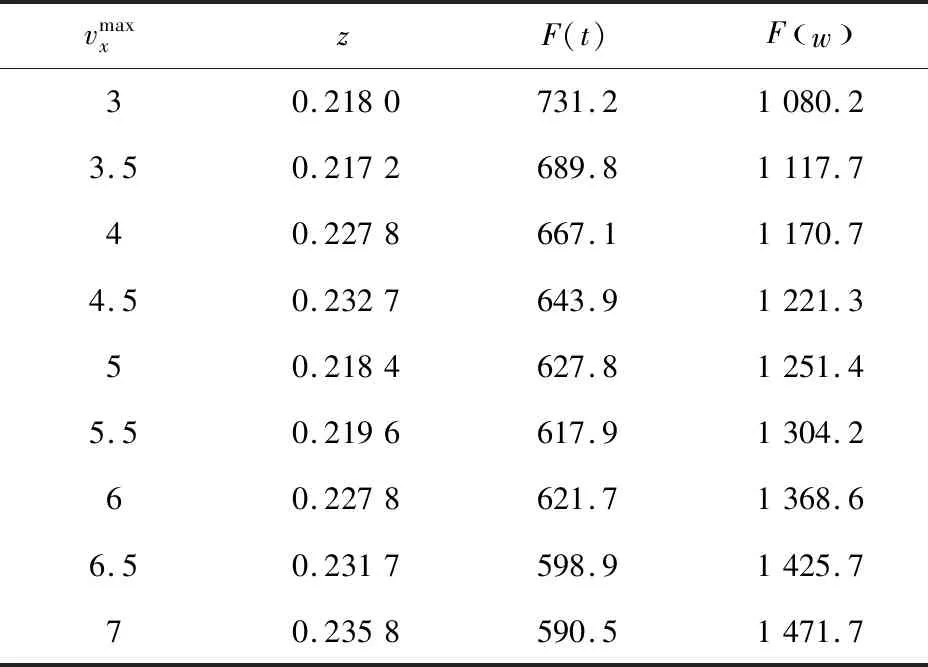

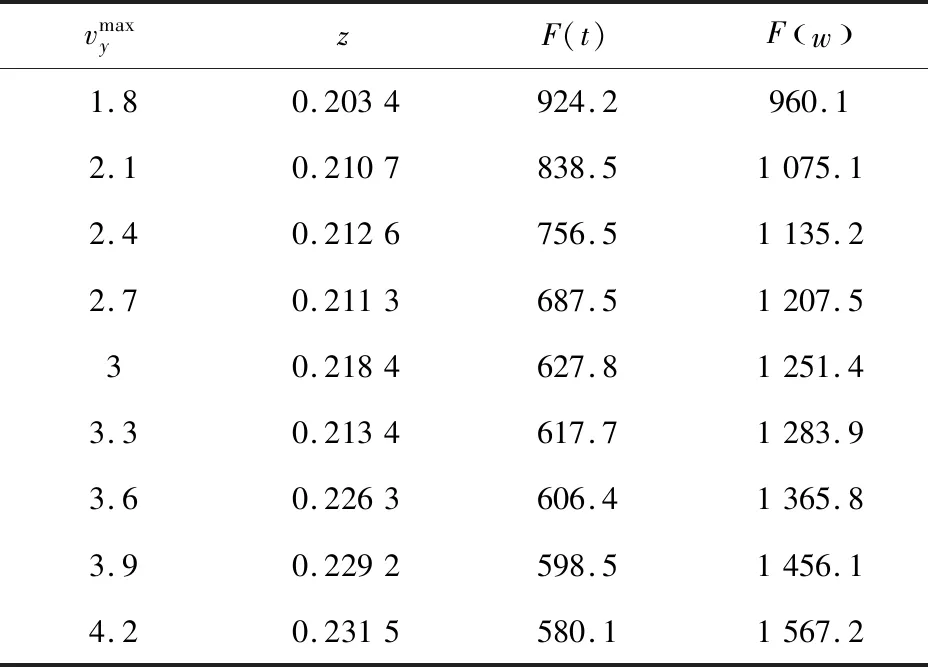
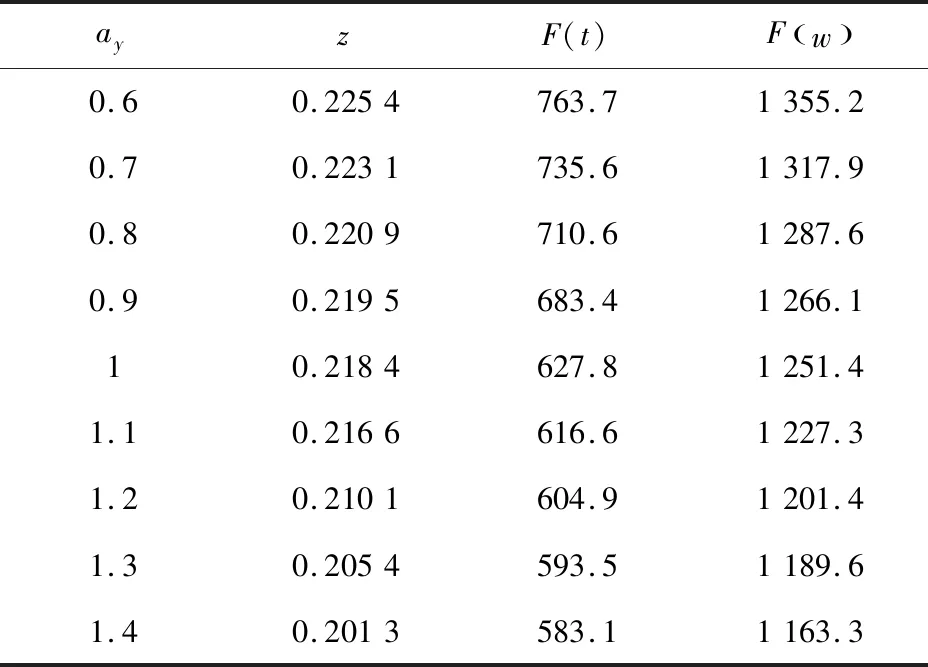
4 结语
