改进的混沌反控制设计及在图像加密中的应用

吕恩胜

(河南应用技术职业学院机电工程学院，郑州 450042)

0 引言

混沌是一种普遍存在的自然现象，研究发现它对一些系统是有益处的，如混沌动力学理论应用于金融稳定[1]、保密通信[2]等领域，取得了显著效果且有巨大的应用前景。因此，研究人员开始关注混沌的产生，致力于非混沌系统进行混沌反控制的研究，目的是使稳定系统混沌化或混沌系统的动力学行为更加复杂[3-4]。采用的方法有：时延反馈法[5]、反馈控制法[6]、及脉冲控制法[7]等。反馈控制法应用最为广泛：Chua等[8-9]先后设计出的经典蔡氏电路和忆阻器蔡氏电路，均为典型的三段式反馈控制系统，至今都是非线性电路研究的典范；梅春草等[10]利用相同和不同状态变量的反馈控制，能对PMSGS系统产生混沌控制和反控制，提高风能利用率；Li等[11]设计了自适应混沌反馈控制(Adaptive Chaos Control，ACC)方法，提高系统的鲁棒性和工作效率；刘爽等[12]设计了一个反馈控制器，对心脏起搏器混沌模型进行控制，使心脏从病态恢复到正常生理机能状态。

为了使非混沌系统产生混沌动力学行为，文献[13]对式(1)线性系统进行混沌反控制设计，原理如式(2)所示。

(1)

(2)

其中，常向量c∈R3，A是3×3的矩阵，B是3×1的矩阵，状态变量x=(x,y,z)T∈R3，S(x)为切换平面，控制器u(x)=(Bx+k)，是设计的核心，k∈R3。矩阵A的特征值为：λ1,2=α±iβ，λ3=-γ，为了使系统式(1)混沌化，要求：α>0，γ>0，根据Lyapunov第一法知道系统式(1)是不稳定的，可得原点是式(1)唯一的平衡点。设计一个合适的矩阵B，使得A+B是一个稳定矩阵，A+B的所有特征值实部都是负值；再设计一个合适的参数k，使得(A+B)x+k=0的解位于区域{x∈R3，S(x)>c}中。使得系统在S(x)切换平面两侧之间来回跳跃，可得到一个简单的控制系统，该系统是分段线性的，是混沌的。

针对文献[13]提出的混沌反控制系统，文献[6]也做过研究，设计的sign(z)较为陡峭，工程中难以实现。为了使它在工程领域中更好地发挥其应用价值，有必要做进一步的研究，设计出更合适的混沌反控制方案。设计通用的矩阵A和分段线性状态反馈切换控制器，得到新的混沌系统，通过调节其系数可以实现不同的混沌反控制，丰富原系统的混沌动力学行为，新的混沌系统具有更丰富的随机性及初值敏感性，在图像加密的应用中具有一定的优势。

1 镜像混沌吸引子设计

文献[13]设计的混沌吸引子位于z=0平面上侧空间，设计新的u(x)控制器和S(x)切换平面，目的是使生成的混沌吸引子与文献[13]中的混沌吸引子关于z=0平面镜像对称，设计的控制器u(x)为

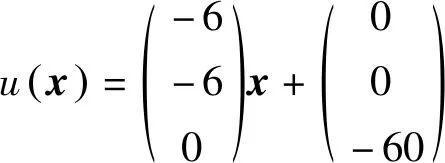
(3)

设计的切换平面S(x)为

(4)

新的混沌系统为

(5)

2 对称混沌吸引子设计

文献[13]研究的只是一个特例，将系统式(1)、(2)中矩阵A通用化，即

(6)

为了将式(3)和文献[13]的控制器融合，设计的u(x)控制器如式(7)所示。

(7)

研究发现，式(7)控制器u(x)，它的前两段是分段线性的，但没有考虑到z=0的情况，为此设计饱和函数sat(z)，其中p>0为增益，实现了变量z的连续性，能将文献[13]设计的上吸引子和式(5)的下吸引子连接在一起。当m=n>0，e=f>0，d1=d2>0时，式(7)的控制器是关于z=0平面对称的。

设计的sat(z)函数

(8)

在式(7)的控制器中，当z>0时，负值-pz/τ<0迫使轨道进入z<0空间；当z<0时，正值-pz/τ>0迫使轨道进入z>0空间。τ<1，τ越小sat(z)函数越陡峭，轨道切换速度越快，但是物理实现困难，本文τ=0.01。

再次得到的新混沌系统为

(9)

设a=20，b=20，c=-15，m=n=5，e=f=12，d1=d2=6，p=1，在MATLAB软件上采用Runge-Kutta方法仿真系统式(9)，得到的对称混沌吸引子如图2所示，设a从0到5变化时，其余参数不变，图3表明，该系统的最大Lyapunov指数(LE)大于零，则此时系统处于混沌状态。

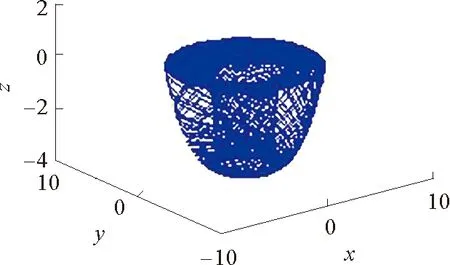
图1 镜像混沌吸引子Fig.1 Mirror chaotic attractor

图2 对称混沌吸引子Fig.2 Symmetric chaotic attractor

图3 最大LEFig.3 Maximum LE

3 混沌动力学行为分析

3.1 定义域

式(7)表示的控制器u(x)，其定义域，可以细分为3个区

(10)

3.2 对称性

对于任何参数，系统式(9)的x,y坐标做变换，(x，y，z)→(-x，-y，z)，系统的模型保持不变，且关于z=0平面是对称的。

3.3 耗散性

设定：a>0，c<-2a，m>0，n>0，p>0，在式(10)定义域范围内，式(9)相空间容积V(t)变化率

(11)

可以求得

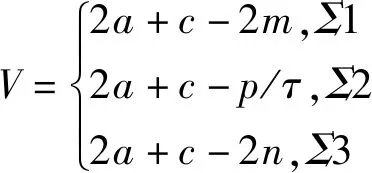
(12)

V(0)为初始容积

(13)

根据设定c<-2a，当t→∞时，V(t)=0，系统是耗散且混沌的，系统轨道以指数速率收缩，最终将限制在R3空间中的一个体积为零的集合上，其混沌动力学行为被限制在其吸引子上。

3.4 系统平衡点的特性

系统式(9)在平衡点O2(0，0，0)的Jacobi矩阵为

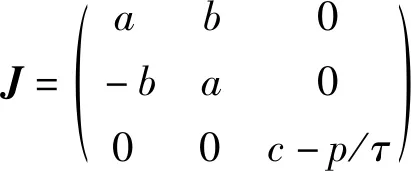
(14)

该Jacobi矩阵的特征方程为

λ3-(2a+c-p/τ)λ2+(2a(c-p/τ)+a2+b2)λ-(a2+b2)(c-p/τ)=0

(15)

根据Routh-Hurwitz判据[14]，若式(15)：a<0，-(2a+c-p/τ)>0，(c-p/τ)<0时，系统式(9)在平衡点O2(0，0，0)是渐近稳定的，否则是不稳定的，又若a=0，c-p/τ<0时，平衡点是系统式(9)的hopf分岔点[15]。

同理：在平衡点O1，当(a-m)<0，-(2a+c)>0，c<0时平衡点是渐近稳定的，否则是不稳定的，又若(a-m)=0，c<0时平衡点是系统式(9)的hopf分岔点；当(a-n)<0，-(2a+c)>0，c<0时在平衡点是渐近稳定的，否则是不稳定的，又若(a-n)=0，c<0时平衡点是系统式(9)的hopf分岔点。

4 参数变化的动力学分析

4.1 参数a变化

初始值(x0，y0，z0)T=(0.1，0.1，-0.1)T，固定参数b=20，c=-15，m=n=5，e=f=12，d1=-d2=6，p=1时，参数a变化，系统动力学行为变化如图4所示。

结合修正指数中相关性分析结果和显著性水平，8个观测变量中Reason1和Preference1间相关系数达到0.51，p<0.001，说明出于会话内容本身原因使用英汉混杂和偏好混杂名词和语气词间存在显著相关关系，似乎表明使用者出于表达专业术语、保持英文原汁原味、汉语中无对应词，避免汉语可能会出现尴尬禁忌，营造气氛等原因使用英汉语码混杂，其混杂词多为名词和语气词，这一发现也较为符合语言交流的实际。

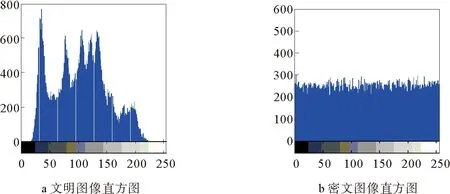
仿真相图的动力学行为表现为：当a<0时，系统轨道衰减振荡，收敛于一个稳定的平衡点；当a=0或5时，系统轨道收敛于极限环；当05时，系统轨道发散。系统仿真结果与3.4节理论分析一致，尤其是0

图4 参数a作用下对称混沌吸引子的相图Fig.4 Phase diagram of symmetric chaotic attractor under the action of parameter a

图5 参数b作用下对称混沌吸引子的相图Fig.5 Phase diagram of symmetric chaotic attractor under the action of parameter b

4.2 参数b变化

初始值(x0，y0，z0)T=(0.1，0.1，-0.1)T，固定参数a=2，c=-15，m=n=5，e=f=12，d1=-d2=6，p=1时，参数b变化，系统动力学行为变化如图5所示。

仿真相图的动力学行为表现为：当b=0时，系统存在一个环；当b≠0时，系统都处于混沌状态。

4.3 参数c变化

初始值(x0，y0，z0)T=(0.1，0.1，-0.1)T，固定参数a=2，b=20，m=n=5，e=f=12，d1=-d2=6，p=1时，参数c变化，系统动力学行为变化如图6所示。

图6 参数c作用下系统式(9)的相图Fig.6 Phase diagram of system (9) under the action of parameter c

仿真相图的动力学行为表现为：当c≥0时，系统发散；当-12≤c<0时，系统轨道衰减振荡，收敛于一个稳定的平衡点；当c<-12时，系统是混沌的。

4.4 参数m、n变化

初始值(x0，y0，z0)T=(0.1，0.1，-0.1)T，固定参数a=2，b=20，c=-15，e=f=12，d1=-d2=6，p=1，参数m，n变化时，系统动力学行为变化如图7所示。

图7 参数m、n作用下对称混沌吸引子的相图Fig.7 Phase diagram of symmetric chaotic attractor under the action of parameters m and n

图8 双重加密流程图Fig.8 Flow chart of dual encryption

5 在图像加密中的应用

1997年Fridrich首次将混沌理论引入图像加密中，由于效率高、操作速度快，伴随互联网技术的快速发展，混沌加密成为近些年研究的热点问题[15-17]。基于保密安全可靠的要求，本研究采用的是双重加密，加密流程如图8所示。

5.1 加密原理

读入明文图像P，获取图像矩阵的行数M和列数N，将明文图像展开成一维向量，记为A，大小为M×N，对向量A的任一点坐标位置(1，j)进行如式(17)所示的改进的Arnold变换，得到新的坐标(pj，qj)，对像素点(1，j)和(1，qj)交换位置，该算法仅考虑列坐标，即不考虑pj的作用。{x0,y0,z0}为初始值,作为密钥1，利用ode45算法计算混沌系统并迭代2×M×N+800次，去除前800点，得到3个序列{xj,yj,zj}，aj和bj为伪随机变量{xj}变换得到，如式(16)所示，多次实验表明，将明文图像展开成一维向量，再将置乱后的一维向量还原成二维矩阵，比起整行整列操作，效果更好，但运算量更大。

x=mod(floor((x+20)×105),10×max(M,N))+1

a=x(1∶M×N)；b=x(M×N+1∶2×M×N)

(16)

(17)

像素位置置乱加密变换：j=1∶M×N，解密逆变换：j=M×N∶-1∶1。

单一的置乱算法，无论多么复杂，无法对抗明文的攻击，因此在置乱后同步扩散算法，设计的扩散处理为加取模和循环左移的算法，明文图像被展开为一维向量Pi，Ci、Si为密文向量。C0为自设密钥2，利用ode45算法再次计算混沌系统并迭代M×N+800次，去除前800点，得到3个序列{xi,yi,zi}，Ci、Si为密文向量伪随机变量{xi}变换得到,如式(18)所示，加密原理如式(19)所示，解密原理如式(20)所示。

L=mod(floor(x×pow2(16))，256)

S=L(1∶M×N)

(18)

Ci=(Ci-1+Si+Pi)mod256；Ci=Ci≪LSB3(Ci-1)

(19)

Pi=Ci≫RSB3(Ci-1)；Pi=(2×256+Ci-Ci-1+Si)mod256

(20)

像素值置乱加密变换：i=1∶M×N，解密逆变换：i=M×N∶-1∶1。

5.2 仿真实验结果

仿真结果表明：图10a、图11和表1表明Lena明文图像在水平、垂直和对角线3个方向上的相关系数接近于1，图10b、12和表1表明密文图像的像素均匀分布，其相关系数接近于0，该加密算法破坏了明文图像的相关特征，表明该加密效果良好。与其他加密方法对比后可知，该加密方案效果更为理想。

图9 图像加密解密效果图Fig.9 Effect drawing of image encryption and decryption

图10 直方图Fig.10 Histogram

图11 明文图像相邻像素分布Fig.11 Adjacent pixel distribution of plaintext image

图12 密文图像相邻像素分布Fig.12 Adjacent pixel distribution of ciphertext image

表1 相邻像素在不同方向上的相关系数Tab.1 Correlation coefficients of adjacent pixels in different directions

6 结论

本文以文献[13]的混沌系统为研究对象，利用改进的反馈控制器，进一步丰富混沌系统动力学行为，讨论了各参数对动力学行为的影响，充分展示了新系统的混沌特性。最后将混沌系统与像素值和像素位置置乱加密算法相结合，极大地增强了系统加密的安全性。在实际中，刻意产生或强化混沌动力学行为是一件有意义的事情，利用混沌的优点可以在生产中取得更加理想的效果。