中国演员和导演网络对电影市场的影响分析

张董极，杨会杰，肖 琴

(1.上海应用技术大学理学院,上海 201418;2.上海理工大学管理学院,上海 200093)

0 引言

近期中国电影产业实现了快速而持续的增长。数据显示，国内电影票房从2012年的170.7亿元增长到2019年的642.7亿元，仅次于美国，位居全球第二。票房年均复合增长率达到20.85%；但是，电影质量年均评分从2005年的7.25到2019年的5.56，下降了23.3%。两个相反的结果表明，随着居民消费水平的上升，人们对高质量电影有了更高的需求。

作为电影质量的定量测度，电影的票房和评分，是多方面共同作用的结果。一方面，国民经济的增长，人们消费水平的提高，决定了电影需求市场的规模和潜力。另一方面，一部电影的成功取决于导演的影响力、演员的知名度和受欢迎程度、剧本质量、电影制作水准和宣传能力等等[1]。其中，导演和主演决定着电影的质量和票房，也因此成为宣传的侧重点。

本文构建了合作网络，讨论了网络拓扑结构与电影票房和评分之间的关系。结果表明，导演的程度中心度对电影质量的影响更大，结构洞对电影的市场竞争力的促进作用大。导演和主演在网络中信息的“共享”和“独享”都可以促进电影质量和市场竞争力。

1 文献回顾

电影网络是社会网络的一种。国内外学者对电影网络进行了不同层次的分析。Watts和Strangatz[2]对好莱坞演员合作网分析发现它具有“小世界”特性。Sorenson[3]等分析了电影制作团队和发行商之间的合作关系对于票房的影响。黄相森[4]建立了一个基于三群落演员的合作网络模型，从导演和演员的双向选择下分析了网络的度分布等。卜彦芳[5]分析了2017—2019年中国电影制片公司的合作关系网络的度和中心度以及网络的凝聚子群效应。李彪等[6]分析了电影制片人和导演之间的合作关系。方爱华等[7]分析了2007—2016年票房前十的华莱坞电影的导演和主演合作的双模网络，验证了网络的小世界性。周静等[8]在导演-演员双模网络的结构特征中发现网络密度低以及中心性明显的特征。

林淼[9]基于项目合作构建了电影公司合作网络，分析了电影项目社会资本对总票房的影响。谭博[10]运用数据可视化的方法分析了电影产业的网络结构。分析电影网络的文章还有很多，然而把票房和评分与导演、主演以及导演-主演双模网络联系起来的很少。

2 数据与统计特征

从中国广电总局和中国统计年鉴收集了1995—2019年电影产量、票房、评分等数据。通过PYTHON爬取了“豆瓣”和“灯塔”2013—2019年的所有上映电影的票房、评分、电影类型、电影效果、电影时长等信息。通过去重、补缺、消除不一致和虚假信息等一系列清洗环节，筛掉了票房小于300万、动画类型、非中国导演的电影，去除了不同时间重复上映的电影。清洗后的数据包括883部电影中774个导演和3 549个主演。883部影片的指导方式中17.1%(151部电影)是由两个及两个以上的导演联合执导，其余83.9%(732部电影)为独立导演执导。图1为1995—2019年中国电影的年产量、年均评分和年总票房等数据。

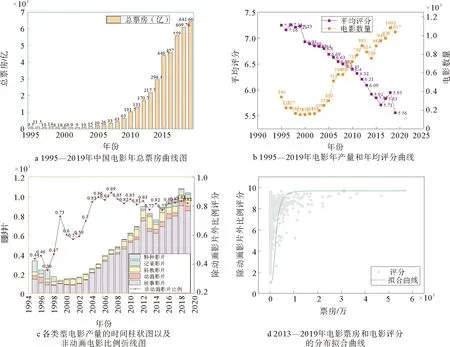
图1 1995—2019电影年总票房、产量、评分以及各类型电影产量曲线图Fig.1 The Curve of total box office, output, score and output of various types of films in 1995—2019

图1a表明中国电影年产量从1995年后经历了几年的低潮期，21世纪后呈现稳步上升。2000年后电影的年产量递增(图1b中橙色曲线)，但年均评分刚好相反(图1b中紫色曲线)，说明在产量增加、大众对文化消费以及审美质量提高的前提下仍存在很多低质量影片，促使电影年均评分持续降低。在所有电影中，故事影片占据着主导地位，是电影发展的主流方向见图1c。图1d中2013—2019年电影票房和评分关系分布曲线呈现似logistic分布，68%左右的电影分布在票房10亿以内且评分7-9的区间，而高票房、高评分的电影在近7年内依旧是少数，低票房、低评分的电影比例相对较大。

3 导演、演员合作关系网络

选取2013—2019年电影的导演和主演作为网络节点。具有主演和导演双重身份的节点认定为导演。导演节点有两种类型：执导导演(不参演电影)和演绎导演(既是该影片的导演又是主演)。两个导演联合执导至少一部影片，建立连接，得到导演联合执导网络。两个演员至少同时出现在一部电影中作为主演连接得到主演合作网络。主演至少参与导演执导的一部电影连接得到导演-主演双模合作网络见图2。图2a中的节点为导演，图2b中的节点为主演。

图2 联合执导网络、主演合作网络、导演-主演双模网络图Fig.2 The co directing network, starring cooperation network, director starring dual-mode network diagram

图3 网络a、b、c的度概率密度对数分布Fig.3 Degree probability density distribution log probability diagrams

3.1 网络的度

节点影响力的一个最直接的指标是节点度。网络A中度排名前七的是：张一白、文牧野、陈凯歌、王晶、徐峥、周星驰、管虎，这些知名导演近些年来联合执导电影较多。网络B中度排名前八的是：林雪、古天乐、任达华、刘德华、彭于晏、王千源、周冬雨、黄晓明，其中排名前5的为来自香港的艺人，说明香港的艺人处于演员合作网络中比较重要的地位。

联合执导网络、主演合作网络以及导演—主演双模网络的度分布，整体上服从幂律分布(见图3)。图3b和3c中，概率密度分段式逐渐增大，这是因为演员网络的层次性和聚类性，说明演员网络的层次性非常明显，演员出演电影具有分层性。在具有相同较小度的范围内呈现出逐渐增多的趋势，表明在较小范围内演员的度和演员数目呈递增关系。根据拟合计算得出网络A、B、C的幂指数分别为γ1≈-2.312±0.049、γ2≈-1.239±0.386、γ3≈-1.078±0.406。

3.2 网络的中心度

表1 3个网络的程度中心度统计Tab.1 Descriptive statistics of centrality of the three networks

3.3 网络的结构洞

个体在网络上的位置比关系的强弱更为重要，决定了个人的信息、资源与权力。为了定量描述这一结构特征，引入了结构洞概念。

图4 主演网络和双模网络的结构洞示意图Fig.4 The structural hole of the leading actor on the network and the director-starring joint network

结构洞的计算采用式(1)的方式：

(1)

其中，pij为节点i,j的连接强度。ci为节点i在网络中的结构约束程度，ci越大，代表节点i的结构洞hi越小。因此要想在竞争中保持优势，就必须建立广泛的联系，同时占据更多的结构洞[10-11]，掌握更多信息。

4 评分与票房的网络回归

观众评分作为电影的质量，电影票房作为电影的市场竞争力，用电影导演和主演的程度中心度和结构洞作为电影评分和票房的主要决定因素，电影的执导方式作为次要决定因素，将电影上映时间、类型、效果、时长作为控制因素，采用2013—2019年的电影实证数据，分别建立电影评分和票房的回归模型。

如果导演也是该电影的演员那么节点度会相对较大。定义导演真实度值为：kd=k-kc，其中k是导演—主演双模网络中导演的度，kc为在主演合作网络中导演作为演员的度。表2为因变量、自变量和控制变量以及其解释。

表2 回归模型变量表以及解释Tab.2 Regression model variable

由于每一部电影存在不止一个的导演和主演，采用程度中心度的平均值和结构洞的平均值作为衡量该电影导演和主演中心度、结构洞的指标。引入调控比例参数α1和α2，电影中心性〈M〉和结构洞〈H〉分别由导演和主演的程度中心度和结构洞共同决定，〈…〉表示平均，公式如式(2)：

〈M〉=α1×〈Director_M〉+(1-α1)×〈Actor_M〉

〈H〉=α2×〈Director_H〉+(1-α2)×〈Actor_H〉

(2)

对需要进行回归的变量进行Z-score标准化处理，将电影的评分和票房根据自变量和控制变量分别进行回归。本文提出假设：

H1网络的程度中心度有助于提高电影的评分；

H2网络的程度中心度有助于提高电影的票房；

H3网络的结构洞有助于提高电影的评分；

H4网络的结构洞有助于提高电影的票房；

H5具有高程度中心度和高结构洞的电影不一定有好的评分，结构洞的提高会抑制程度中心度对电影评分的促进作用；

H6具有高程度中心度和高结构洞的电影不一定有好的票房，结构洞的提高会抑制程度中心度对电影票房的促进作用。

为了对上述假设进行判断，本文考察了10个模型，

模型1score=β0+β1×DR+β2×premiere+β3×types+β4×effect+β5×duration+εn

模型2score=β0+β1×〈H〉+β2×premiere+β3×types+β4×effect+β5×duration+εn

模型3score=β0+β1×〈M〉+β2×premiere+β3×types+β4×effect+β5×duration+εn

模型4score=β0+β1×(〈M〉×〈H〉)+β2×premiere+β3×types+β4×effect+β5×duration+εn

模型5score=β0+β1×〈M〉+β2×〈H〉+β3×(〈M〉×〈H〉)+β4×premiere+β5×types+β6×effect+β7×duration+εn

模型6box=β0+β1×DR+β2×premiere+β3×types+β4×effect+β5×duration+εn

模型7box=β0+β1×〈H〉+β2×premiere+β3×types+β4×effect+β5×duration+εn

模型8box=β0+β1×〈M〉+β2×premiere+β3×types+β4×effect+β5×duration+εn

模型9box=β0+β1×(〈M〉×〈H〉)+β2×premiere+β3×types+β4×effect+β5×duration+εn

模型10box=β0+β1×〈M〉+β2×〈H〉+β3×(〈M〉×〈H〉)+β4×premiere+β5×types+β6×effect+β7×duration+εn

参数β0为常数项参数，β1、β2、β3、β4、β5、β6、β7分别为各个变量的参数，εn为误差，服从正态分布。

模型1和模型6分析的是电影的执导方式DR对电影评分和票房的影响，所以后面的模型就不需考虑电影执导方式对票房和评分的影响。模型2-5联合探析的是电影中心度、结构洞以及两者共同作用对电影评分的影响。模型7-10联合分析的是电影中心度、结构洞以及两者共同作用对电影票房的影响。

在进行回归前，对自变量进行多重共线性检验，采用方差膨胀因子方法。

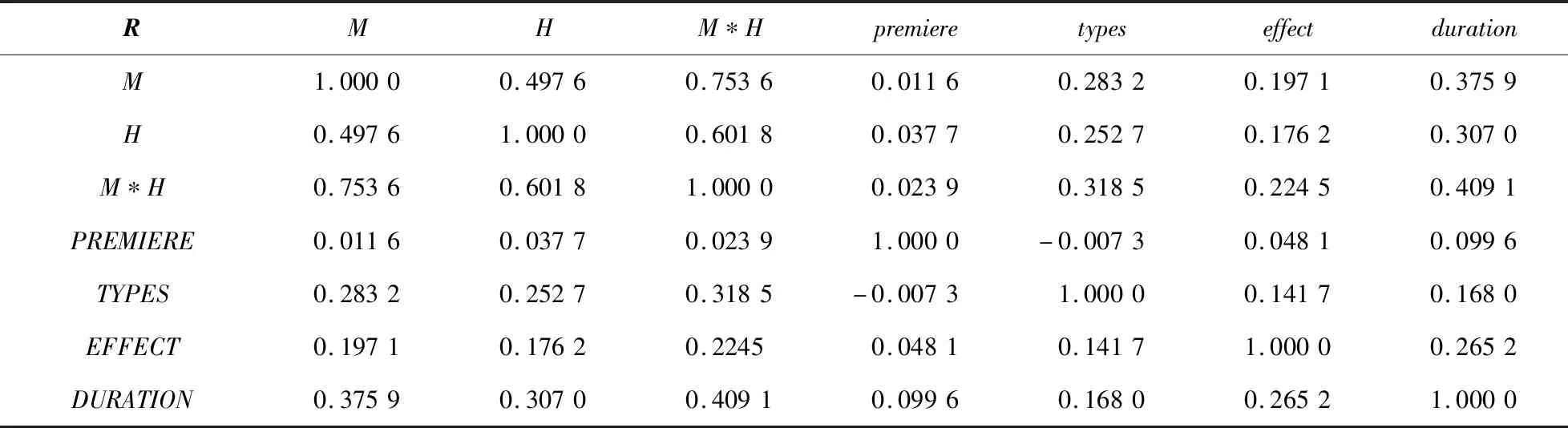
表3 自变量相关系数矩阵RTab.3 Independent variable correlation coefficient matrix R

表3为自变量相关系数矩阵R。方差膨胀因子VIF公式为

(3)

其中，rjj为每一个自变量对应的方差膨胀因子，为R-1相应的对角元素，如果VIF<5，则认为自变量间不存在多重共线性。计算得本文自变量的VIF=4.763 4，因此不存在多重共线性。

假设导演和主演对电影的影响力是相同的，取系数α1=α2=0.5，回归结果如表4所示。

表4 电影评分和各变量的回归模型结果表Tab.4 Movie ratings and regression model

由表4的模型1-5回归结果可知，模型1的回归表明导演的联合执导对电影评分的提高没有显著关系，意味着一部电影的评分与导演是联合执导还是独立执导没有关系。模型2显示程度中心度的增加有利于提高电影的质量，这验证了假设H1是正确的。模型3结果指出结构洞对电影质量的影响不如中心度的影响大，其系数是程度中心度的52%。但结构洞的增加也有利于提高电影的质量，也验证了假设H3的正确性，因此共享比独享更有利于电影质量的提高。两者乘积的系数大小介于中心度和结构洞之间。因此当一部电影同时拥有两者的优势时并不会显著提高电影的质量，两者不具有叠加效应(同时拥有高中心度和高结构洞)的电影的质量并不一定高，验证了假设H5是正确的。

表5 电影票房以及变量的回归模型结果表Tab.5 Movie box office and regression model

从表5的结果可以看出，模型6表明导演的联合执导对电影票房有促进作用，这和电影质量结果是不一样的，说明多个导演合作执导能增加电影的票房，显然这种联合执导使得电影更具市场竞争力。模型7～8说明中心度和结构洞对电影的票房都有促进作用，中心度的影响更大。这很好地验证了假设H2和H4。模型9表明两者的乘积对票房有正向的影响，但没有程度中心度单独回归的影响大，且模型10三者共同回归系数变得不显著，说明中心度和结构洞对票房的促进作用也不具有叠加效应。所以增加网络中心度的同时，降低网络的结构洞可以使得这种正向作用更大，假设H6得证。

图5针对调控比例参数变化对评分和票房回归系数的影响进行分析。其中图5a是模型2和模型7中α1从0-1的变化过程中的中心度系数曲线，图5b是模型3和模型8中α2从0-1改变时的结构洞系数曲线。

图5a显示：程度中心度对电影评分和票房的正向影响随着导演中心度所占比例增加和主演的降低呈现先上升后下降的趋势。在导演中心度贡献率为0.215时，这种正向影响相等，随着导演贡献率的增加，中心度对评分的促进作用更大。说明导演的中心度对电影评分的影响更大。结构洞系数则呈现了单调的曲线，这种单调曲线说明导演对电影结构洞贡献率越大，主演贡献率越小，结构洞对评分的促进作用越小，对票房的促进作用越大。

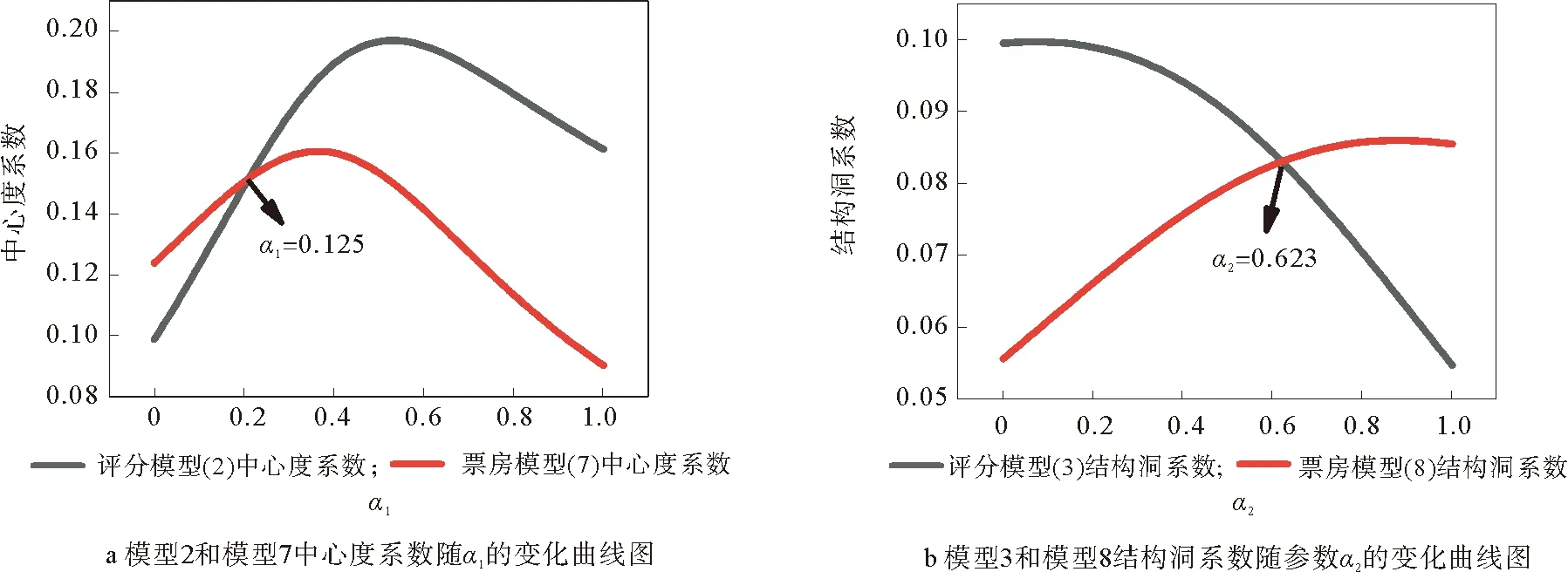
图5 模型2和7以及模型3和8中心度系数和结构洞系数随α1和α2变化曲线图Fig.5 The variation curve of centrality coefficient of model 2 and model 7 with α1 and the variation curve of structural hole coefficient of model 3 and model 8 with parameter α2

图6a为模型5和模型10中固定α2时，α1的变化趋势，当结构洞比例参数α2一定时，随着中心度比例参数α1的增大中心度和结构洞的乘积对评分的影响系数先增大后减小，在0.6邻域内达到峰值。图5b中当中心度比例参数α1一定时，随着结构洞比例参数α2的增大中心度和结构洞的乘积系数持续减小。说明导演的结构洞对电影票房的正向作用更大，在导演和主演对电影中心度的贡献比例为40%时最大，因此提升电影的票房应该降低演员合作网络中主演的结构洞。

5 结论与讨论

运用2013—2019年中国电影导演、主演的参演数据构建了联合执导网络、主演合作网络以及导演-主演双模合作网络，对网络的中心度和结构洞与电影的评分和票房的关系进行了回归分析，构建了回归模型，得出导演之间合作交流、分享经验有助于拍出高票房的电影，但对电影的质量没有影响。不论是程度中心度的提高还是结构洞的增加都能够显著提高电影的质量和票房。当一部电影同时拥有程度中心度与结构洞二者的优势时，不会显著提高其质量和票房，说明并不是拥有的资源越多就越有优势。为使电影具有更好的质量和市场竞争力，应同时提高主演合作网络以及导演-主演双模网络的中心度且降低两者网络的结构洞。

本文仍有一些不足之处如数据来源有限，没有考虑制片方、编剧等重要因素，电影的质量和竞争力仅仅通过评分和票房衡量，具有一定的偏差。在后续研究中，可以扩大时间跨度，考虑编剧、制片方等多种因素，为导演拍出具有高市场竞争力的电影提供指导建议。