离散事件系统中的攻击检测和修复
2023-01-11宋运忠
闫 安,宋运忠
(河南理工大学电气工程与自动化学院,河南 焦作 454000)
0 引言
近年来,随着反馈控制系统的网络组件的增加,使得系统越来越容易受到攻击。关于系统安全性的研究愈发得到重视。所以,在系统中嵌入防御机制,能够减少攻击对系统的影响,对确保控制系统的稳定性、安全性具有重要的意义[1-2]。经典的闭环控制系统结构如图1所示,包括传感器,监督器,执行器和被控对象4部分。我们采用离散事件系统理论来对该系统进行建模。假设执行器和传感器的通讯线路可以被攻击者注入错误信号,就可能引发安全事故。本文主要考虑启动执行器的攻击(即,AE攻击)情况。在某些情况下,一部分事件是比较脆弱的,因而能被攻击者更改,从而损害系统的安全性。而通常,该攻击是不能被直接观察到的。
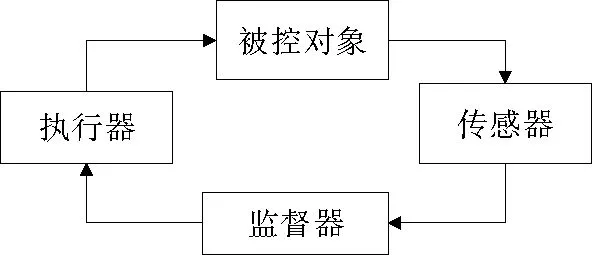
图1 闭环控制系统的结构Fig.1 Closed-loop control system architecture
本文的工作是对网络系统中的异常/入侵检测工作的补充[3-5]。不关注攻击者是如何渗透的,只关注检测攻击及其对控制系统的影响。
在文献[6]中,作者研究了离散事件的监控系统的入侵检测和预防,并设计了在正常运行和攻击后都达到规范的监控器。其重点是寻找语言条件,在这种语言条件下,监督器可以在达到给定规范的同时防止出现攻击时的不安全行为,被称为禁用语言,它与本文提到的安全可控性条件有几个相似之处。入侵检测和预防的问题与容错监控问题有关,容错监控问题在文献[7-10]中研究得很好,其中鲁棒监控器被设计为即使在系统出现故障时也能保持规范。
本文的主要工作如下:首先,本文基于文献[11]给出了AE攻击下监控系统的数学模型和在线检测攻击的防御策略。之后,引入AE安全可控性的定义,并给出了诊断器算法,以验证系统的AE安全可控性。最后,基于AE安全可控性,提出了修复系统的算法。
1 离散事件系统
通常将一个被控对象模型设为一个确定有限状态自动机,建模为五元组G=(X,E,f,x0,Xm)。其中,X是有限状态集,E为事件集,f:X×E*→X表示转移函数,x0为初始状态,Xm为标记状态集。G生成的语言记为L(G)={s∈E*:f(x0,s) is defined},其产生的标记语言为Lm(G)={s∈E*:f(x0,s)∈Xm}。当给定事件集E′⊂E,状态集x∈X时,那么关于E′⊂E和x∈X的可到达的状态的集合定义为Reach(G,x,E′)={x′∈X:(∃s∈E′*)[f(x,s)=x′]}。在状态x处的G的活跃事件集定义为ΓG(x)。
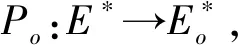
1)Po(ε)=ε
2)Po(σ)=σσ∈Eo
3)Po(σ)=εσ∈Euo
4)Po(sσ)=Po(s)Po(σ)s∈E*,σ∈E
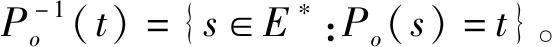
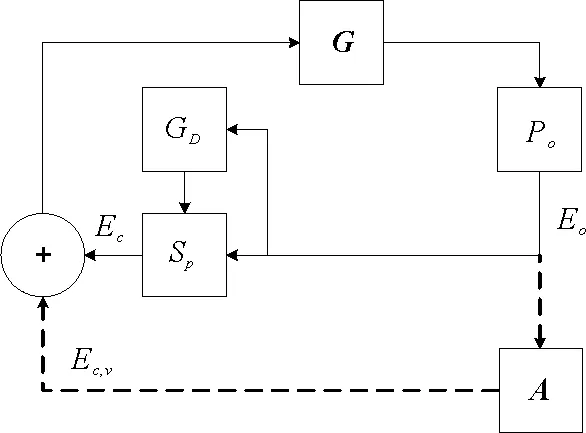
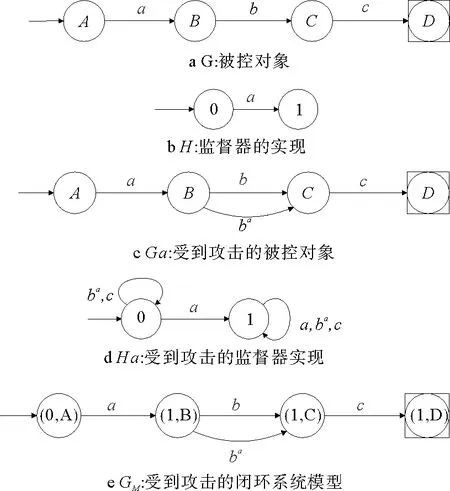
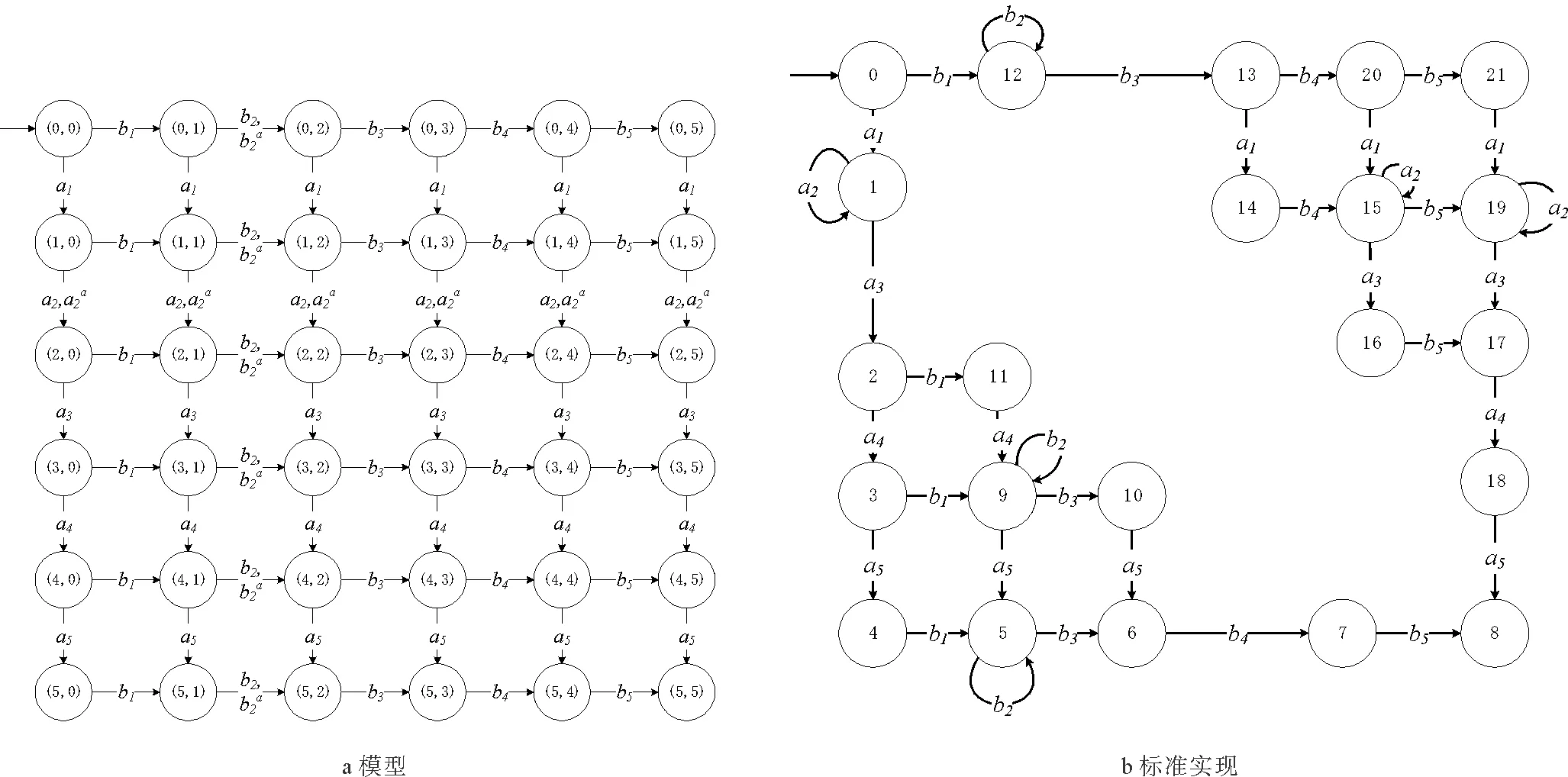
所有的映射和逆映射运算都可以扩展到整个语言上。当s′为s的严格前缀时,记作s′ 图2 处于攻击下的闭环控制系统结构Fig.2 The control system architecture under attack 处于攻击下的模型如图2所示。被控对象为G,由部分可观的监督器Sp控制。设E为G的事件集,执行器可控事件集为Ec⊆E,而传感器由可观事件集为Eo⊂E。监督器通过从集合E到集合Eo的映射来观测被控对象的可观事件的发生。模块A表示攻击者,它可以访问Ec的子集,用Ec,v⊂Ec表示脆弱的执行器事件集合。该集合是基于系统设计预定义的。GD模块是检测攻击的模块,即入侵检测模块。 首先,构筑一个受到AE攻击的闭环模型,并采用两种算子对攻击行为进行建模:膨胀[14]和压缩运算[15]。 其具体的性质为 1)D(ε)={ε} 2)D(σ)={σ}σ∈EEc,v 3)D(σ)={σ,σa}σ∈Ec,v 4)D(sσ)=D(s)D(σ)s∈E*,σ∈E 具体性质为 1)C(ε)=ε 2)C(σ)=σσ∈E 上述的膨胀和压缩操作都可以应用到整个语言,即 D(L)=∪s∈LD(s),C(La)=∪sa∈LaC(sa) 在算法1[11]中描述了受到AE攻击的闭环系统。其中H为监督器Sp的有限状态机实现。 算法1AE攻击的模型算法 输入:G=(X,E,f,x0)和H=(XH,E,fH,x0,H):被控对象和监督器各自的标准实现Eo,Ec和Ec,v:可观,可控和易受攻击的事件集合 输出:处于AE攻击下的闭环系统GM=(XM,Ea,fM,x0,M) 1)构造Ga=(X,Ea,fa,x0)其中fa(x,σa):=f(x,C(σa)),f(x,C(σa))! 2)构造Ha=(XH,Ea,fHa,x0)其中 3)计算GM=Ha||Ga 其中,“!”表示已定义,“∨”表示未定义。 一个被控对象如图3a所示,其中Ec=Ec,v={b},状态D为不安全的状态。监督器的实现如图3b所示,此处,监督器只能在状态B处中止事件b,防止被控对象到达不安全的状态D。通过算法1构建了系统受到AE攻击之后的模型,ba表示攻击事件。图3c为受到攻击后的被控对象模型,图3d为受到攻击的监督器模型。受到攻击后的系统GM如图3e所示。系统最终通过不可控事件c到达了不安全状态D。 图3 例1Fig.3 Example 1 在例1中,AE攻击时,被控对象可能会偏离监督器执行的规范并达到不安全的状态。对此,可以设计一个攻击检测模块在攻击行为后将系统切换到“安全模式”。在某些情况下,由于系统本身设计的缺陷,该策略可能无法保证系统的安全性。本文将所有不安全状态的集合视为一个状态。这与Sp所实现的原始规范K完全不同。虽然假定所有Sp/G达到的所有状态都是安全的,但这并不是说Sp/G不能达到的状态是不安全的。用Xf表示不安全的状态。Xf是X的子集,它捕获的是对被控对象造成物理伤害的状态。 该算法基于文献[16]的“安全可控性”和“禁止语言”。通过利用上一节的模型GM,将攻击检测问题描述为故障诊断问题,其中故障事件是攻击者对脆弱事件的攻击。本文设计了一个入侵检测模块以监视被控对象的输出,并在攻击被检测到的时候通知监督器,终止所有行为。 定义1AE安全可控性 图4 AE安全可控性定义Fig.4 The definition of AE safety controllability GM的构造程序和AE安全可控性的定义中的条件可以得到推论1。 为了测试一个系统是否是AE安全可控的,本文提供了一个依赖于诊断器[17-18]自动机的算法程序。 该诊断器验证的问题是是否能在被控对象达到不安全状态之前检测到攻击和监督器能否禁用事件以阻止被控对象达到Xf。AE安全可控性是基于文献[16]提出的,所以此处要引入诊断器中首次进入某些确定状态集的定义。 定义2首次进入的确定状态的集合 设Gd=(Qd,Eo,fd,q0,d)为由给定的被控对象和相应的标签自动机构造的诊断器。 定义:QYN={q∈Qd:qis uncertain},QN={q∈Qd:qis normal},QY={q∈Qd:qis certain}。 则首次进入确定状态的集合是: FC={q∈QY:(∃q′∈QYN,∃σ∈Eo)[fd(q′,σ)=q]}。 由此可以引出算法2,基于诊断器的算法,用于测试AE安全可控性。 算法2检测AE安全可控性的诊断器算法 输出: AE安全可控性∈{true,false}。 1)构造Gl=GM||Al,其中Al如图5所示; 2)计算诊断器Gd=Obs(Gl,Ea,uo),其中Ea,uo=Euo∪D(Ec,v∩Euo); 4)AE安全可控性=false; 5)else根据定义5计算FC; 7) AE安全可控性=false; 8)else; 11) AE安全可控性=false; 12)elseAE安全可控性=true。 注意,诊断器总是会检测到σ∈Ec,v∩Eo中对脆弱事件的攻击,因为对应的σa是可观的。然而,在这种情况下,被控对象仍然可能通过不可控和受攻击的执行器事件达到不安全状态,违反AE安全可控性。因此,定义1中的条件仍然需要测试,如算法2所述。 例1中,在图3e中展示AE攻击下的闭环系统。此处按照算法2来测试系统是否为AE安全可控的,得到的Gl如图6所示。 图5 标签自动机AlFig.5 Label Automata Al 图6 自动机GlFig.6 Automata Gl 基于算法2,当一个系统不能满足AE安全可控性时,我们能够按照一定的规则对该系统进行修改,使其能够满足该AE安全可控性条件。由此,提出了算法3。 算法3修复系统AE安全可控性的算法 输入:违反AE安全可控性的系统 输出:满足AE安全可控性的系统 endwhile 2)根据定义2计算FC endwhile 4)计算Xuc endwhile 算法3是基于算法2所建立的,通过对算法2的逐步补充验证而构造。 例1中,我们在图3e中展示AE攻击下的闭环系统。此处按照算法3来修复系统,如图7所示。经过算法3检测,可以得知其是在第5)步中,违反了判断条件,此处,可以通过添加一个可控且可观的事件d使得系统满足AE安全可控性。如图7所示。 图7中的虚线箭头表示事件将不会发生,从而避免了系统进入到不安全的状态。 图7 修改后的满足AE安全可控性的系统Fig.7 Modified system that meets the safety and controllability of AE 图8 一段有检测器和红绿灯的铁路Fig.8 A railway line with light and detector 可控事件集为Ec={a1,b1,a2,b2,a4,b4},可观事件集为Eo={a1,b1,a3,b3,a4,b4,a5,b5}。控制目标是希望两列车在通过这一段路时,为了保证不碰撞,不允许两列车同时出现在同一路段(仅指S1-S4)。 图9 被控对象的模型和Sp的标准实现Fig.9 The plant mode and the standard realization of P-supervisor 图10是受到AE攻击的监督器和闭环系统。 图10 受到AE攻击的监督器和闭环系统Fig.10 The supervisor and closed-loop systems under AE-attack 图11 修复后的闭环系统Fig.11 The repaired closed-loop systems 显然,通过上述的举措,使得该段轨道即使是在受到AE攻击时,也能够保持安全性。 本文主要研究了离散事件系统中的入侵检测,防御以及修复问题。基于受到AE攻击的系统模型,引入了AE安全可控性的定义,得到了一种能够对系统的AE安全可控性进行检测的诊断器算法。并在检测后禁用所有可控事件,防止系统到达不安全状态。最后,当系统不满足AE安全可控性时,提出了一种修复算法,使其确保了系统的安全可控。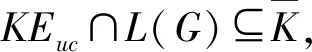
2 受到AE攻击的系统建模
2.1 攻击建模
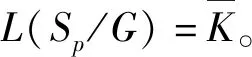
2.2 AE攻击下的闭环系统
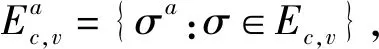
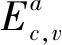
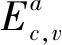
2.3 例1
3 AE攻击的检测与系统修复
3.1 检测和防御策略
3.2 AE安全可控性
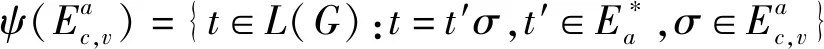
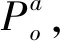
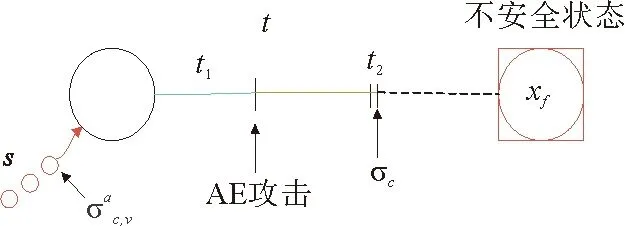
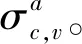
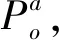
3.3 AE安全可控性的诊断
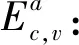
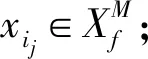
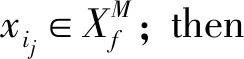
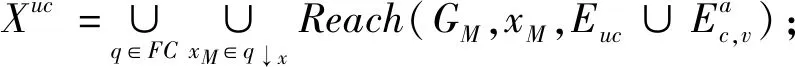
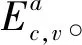
3.4 例2
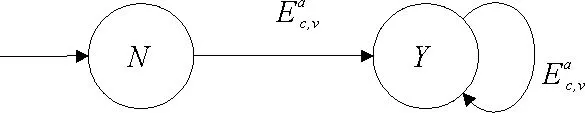

3.5 系统AE安全可控性的修复算法
3.6 例3
4 实例
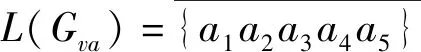

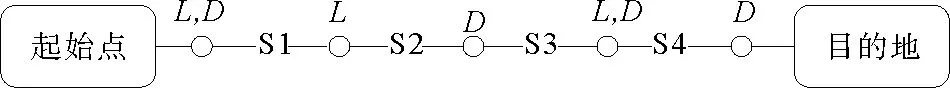
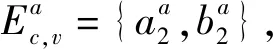
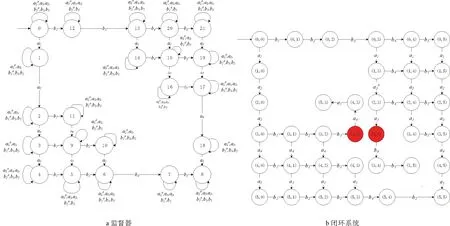
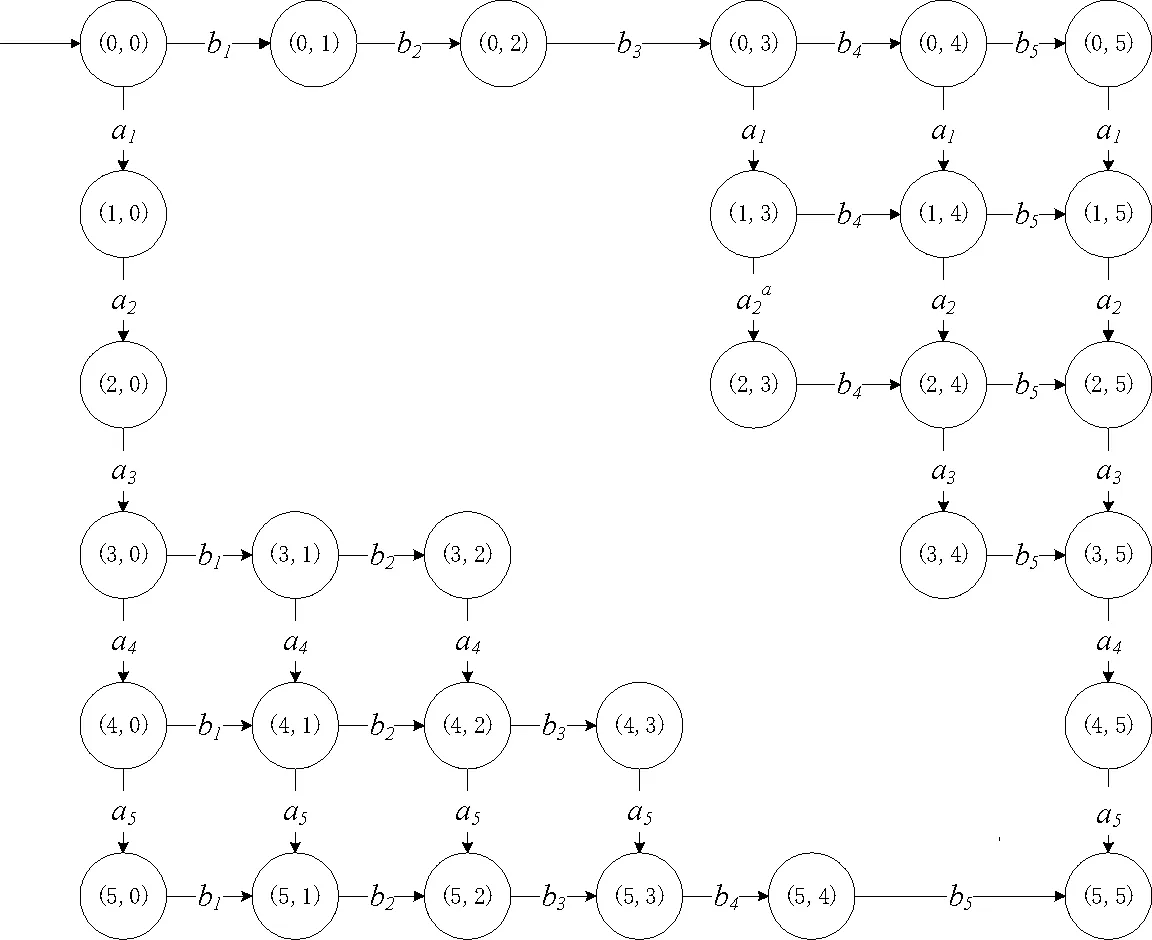
5 结语
