考虑管土作用及内流影响的缓波型立管动力响应分析
2023-01-11丁正旺张火明管卫兵陆萍蓝
丁正旺,张火明,管卫兵,陆萍蓝
(1.中国计量大学 计量测试工程学院,浙江 杭州 310018;2.自然资源部第二海洋研究所,浙江 杭州 310012;3.中国计量大学 工程训练中心,浙江 杭州 310018)
1896年美国在加州海岸附近打出第一口海洋油井后,人类对海洋油气的探索从未止步。近几十年来,随着社会的发展与人口激增,陆上能源的消耗量越来越大,因此由陆向海,由浅向深是能源开采的必然趋势。新发现的油气资源有很大一部分位于深海[1-3],这表明深海油气资源的开采在未来将会占据更大的比重。油气主要依靠立管从海底运输至海面,当前广泛应用的是自由悬链线立管,但随着开采深度的增加及深海环境的愈发复杂,自由悬链线立管与海床之间的强相互作用问题更加突出,于是缓波型结构的悬链线立管顺势而生[4],即LWSCR。
国内外学者当前对缓波型立管的研究多集中于涡激振动、结构优化等方面,在管土作用方面的研究较少。周岳等[5]基于等效原则将缓波型立管转换成直管进行分析,针对不同浮体段覆盖率对缓波形立管涡激振动的影响规律进行探讨,得到了立管不同轴向位置的运动轨迹;王金龙等[6]利用梁理论及有限差分法建立缓波形立管力学分析模型,发现平台和海流载荷对立管力学性能影响显著;孙丽萍等[7]利用数值模拟的方法对立管相关布置参数进行了分析,相关结论可为立管设计提供参考;Kim等[8]研究指出钢制缓波立管的应力、弯曲及疲劳损伤较于传统立管能够得到有效减缓;赵园等[9]将遗传算法应用在LWSCR的优化设计中,通过对各段长度以及浮力材密度进行调整,对立管静态、动态等效应力进行了优化;于帅男等[10]将单波构型优化为双波构型,利用集中质量法对两种结构形式进行分析,证明了双波构型的张力及弯曲特性更优,并对双波构型的立管进行敏感性分析;Li等[11]分析了LWSCR的悬挂角、浮力块位置分布等可变因素对立管动力响应的影响。
为保障缓波型立管的工作安全,基于集中质量法以及Randolph和Quiggin提出的非线性海床模型,我们利用OrcaFlex软件建立浮体-立管-海床的数值模型,并考虑管土相互作用,同时利用控制变量法,以浮体偏移、海床模型、土体属性参数和管内流体为变量,对缓波型立管的动力响应进行敏感性分析。
1 管土作用模型
悬链线式立管的构型会导致触地段与海床土体接触,在浮体运动及外部载荷的激励下,立管触地部分与海床发生持续相互作用,整个过程具有明显的非线性特征,管土作用过程如图1。在作用过程中,海床表面会形成沟槽,其最深处深度可达管径的数倍[12],这会对立管触地段造成较大影响并诱发立管疲劳破坏。RQ土体模型是非线性模型,图2给出了RQ模型的抗力-深度曲线,体现了管土相互作用过程[13],并在立管贯入阶段考虑了土体的弱化反应,过程中土体阻力与土体吸力分别表示为:
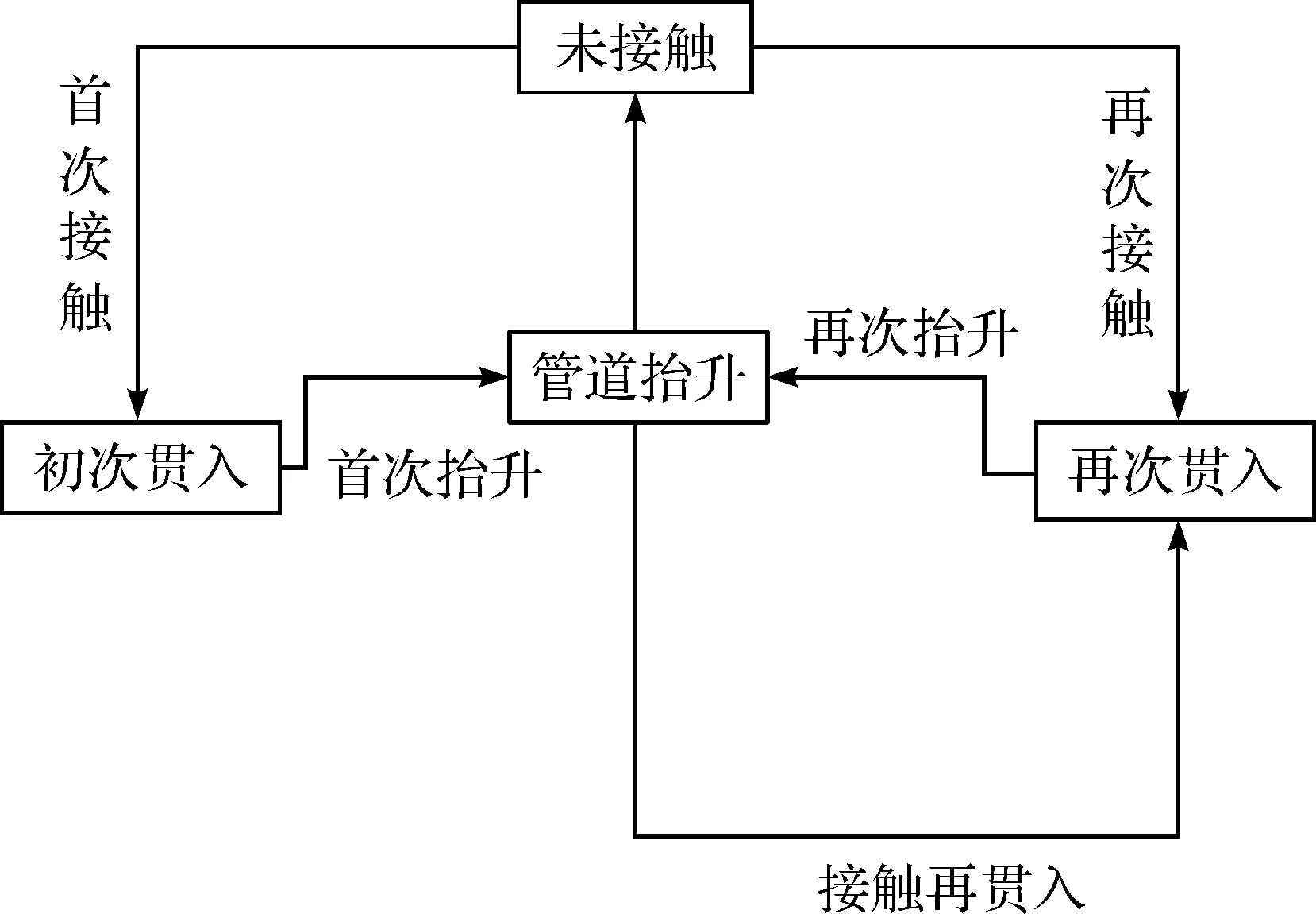
图1 管-土作用过程
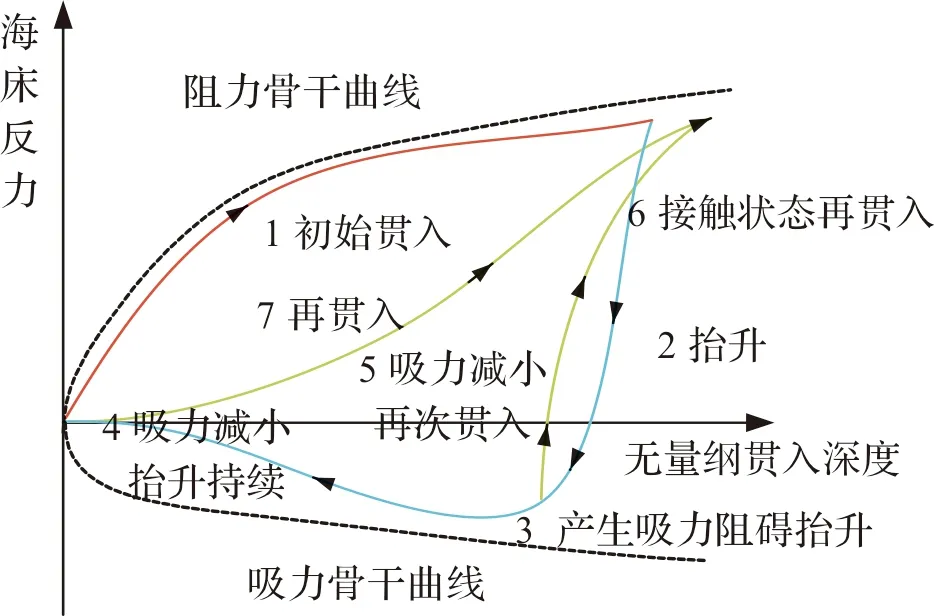
图2 R-Q土体曲线
Pu(z)=Nc(z/D)Su(z)D,
(1)
Pu-suc=-fsucPu(z)。
(2)
其中,Pu(z)表示土体阻力,Pu-suc(z)表示土体吸力,Nc(z/D)是承载因子,z是立管的贯入深度,D是管径,fsuc是无量纲吸力因子,Su是当贯入深度为z时的土体抗剪强度:
Su(z)=Suo+Sugz。
(3)
式(3)中,Suo是土体表面抗剪强度,Sug是抗剪强度梯度。
为对立管与海床接触时的三个阶段曲线进行数学表述,引入了无量纲贯入深度ζ[14],对进行无量纲化可得到ζ:
ζ=z/(D/Kmax)。
(4)
式(4)中Kmax是非线性土体刚度,在再贯入段考虑到土体弱化,具体表现为立管上升后再贯入时阻力的衰减:
Pmax=(z)=ERP(z)PIP(z)。
(5)
其中是初始贯入时的阻力可表示为
ERP(z)=emin[0,-λrep+(z-zp=0)/(λsuczmax)]。
(6)
式(6)中zmax表示最大贯入深度,zp=0是土体吸力出现时的贯入深度,λsuc是吸力衰减参数,λrep是再贯入偏移参数。
2 数值模型
以1 500 m水深的缓波型立管为研究对象,顶部浮体为某半潜式平台与立管相连,在OrcaFlex中建立集中质量模型,模型示意图如图3,立管参数如表1[15]。

表1 缓波立管参数

图3 模型示意图
为对立管进行动态计算,选择了南海百年一遇的海况,表层流速1.197 m/s,风浪流来向角为0°。海床土体对立管触地部分影响较大,故采用非线性海床模型进行模拟,参数见表2。

表2 土体模型参数
3 计算结果分析
3.1 静力分析
首先对整体数值模型完成静力计算,静力分析能够得到立管的初始状态和受力特点。浮体在作业过程中,受到波流载荷的影响,不会长久处于初始位置,会发生一段距离的偏移,在完全系泊状态下,浮体偏移距离能达到6%~10%的水深深度。根据浮体位置离立管触地点的远近将浮体位置分为初始位置、近偏移位置和远偏移位置。浮体远点偏移位置在初始位置左侧,距离立管的触地点较远;近点偏移位置距离立管触地点较接近,在初始位置右侧。本文设置浮体偏移距离为130 m。
图4为浮体偏移后的立管构型,图5为不同偏移下的有效张力。可以看出远偏到近偏状态,立管的横跨距离逐渐减小,浮力段波形渐拱;在重力的作用下,立管有效张力随着长度延伸而变化,在达到前段构型的低端后,随着管长的增加而增加,到立管浮力段后,此时立管所受浮力大于重力,张力开始降低,当达到立管浮力段的顶部时达到最低值,之后张力再次升高,直至浮力段末端达到峰值。之后张力随着管长的增加而减小,直至触地,在远偏状态下立管的整体线形绷紧,张力变大;近偏状态的变化与之相反。

图4 静态构型

图5 静态有效张力
立管的von Mises应力如图6,在立管悬挂点附近、立管构型的波峰波谷处、触地点附近较大。这都是由于立管浮力段提供的浮力使得立管局部发生较大的弯曲变形导致。图7显示弯矩峰值会出现三处,主要位于立管构型的波峰、波谷处以及立管触地点附近,这几部分的立管曲率也较大。从应力和弯矩的分布图的相比不难看出,两者的峰值分布趋于一致,这些都是立管强度破坏的重点区,因此在进行立管设计时要重点关注。
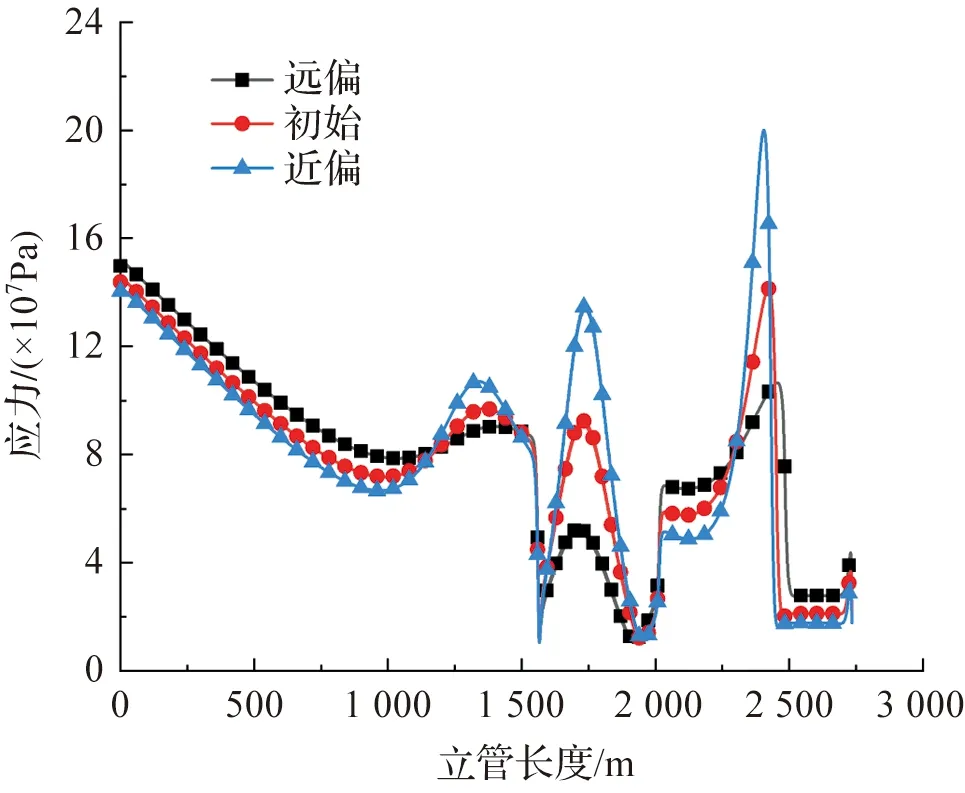
图6 静态应力
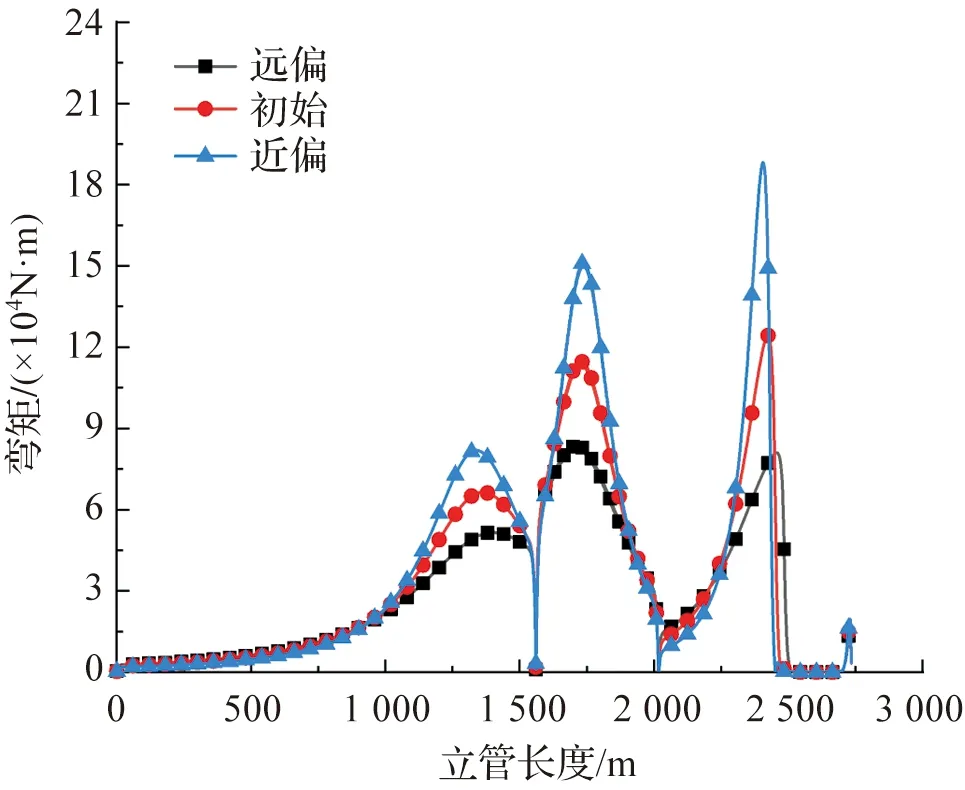
图7 静态弯矩

图8 初始工况下贯入深度和管土作用力

图9 近偏移工况下贯入深度和管土作用力

图10 远偏移工况下贯入深度和管土作用力
图8~10是立管在三种浮体偏移状态下的贯入深度和管土作用力曲线。立管贯入深度和管土作用力分别在各自触地点之后约7 m,11 m,10 m处达到最大值,并在触地点后约35 m趋于稳定。在三类工况下形成的沟槽的形状也是各有不同。
表3为三种偏移工况下静力分析的部分结果,可以看出,浮体偏移对立管触地段力学性能影响显著,在远偏状态下的立管贯入深度、应力等降低;近偏状态的变化与之相反,此时立管的贯入深度最大,形成的沟渠最深,弯矩最大。因此在进行立管设计时要充分考虑到不同工作状态下的参数选择。
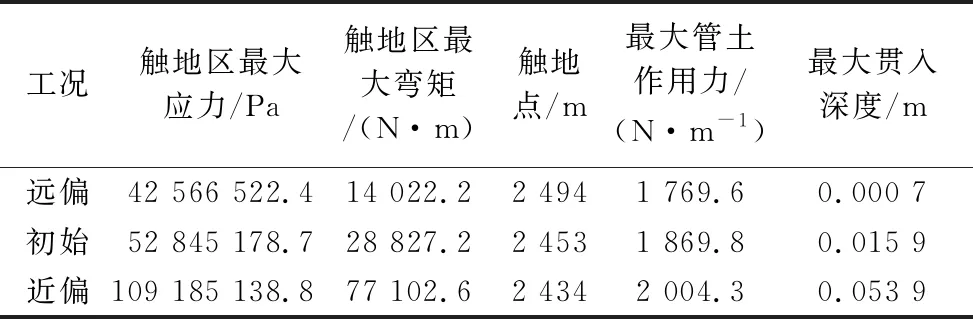
表3 静力分析相关结果
3.2 动态分析
静力分析是立管动态分析的前提,完成静力分析后,通过对半潜式平台加载外部载荷,浮体会产生六自由度的运动并带动立管产生动响应,诱发立管与海床土体发生持续的管土接触作用,这种持续作用对立管的结构强度和疲劳损伤等有着极大影响。为了对浮体偏移、海床参数及管道内流对LWSCR动态响应的影响进行探究,通过设置多种工况来进行对照,以初始状态为对照组,分析LWSCR在各类工况下的响应规律。
3.2.1 浮体偏移的影响
0°来流角下浮体在三种偏移工况下的动态计算结果如图11(a)—(e)及表4,可看出立管应力在近偏状态下最大,其次是初始状态、远偏状态;对触地区的弯矩、贯入深度而言,三种偏移下的大小关系为:近偏>零偏>远偏。立管的有效张力在远偏状态下最大,最大值在立管顶部接头处,可见远偏移工况对于立管顶部接头区域而言是较危险工况。当浮体接近触地点时,触地区管土作用加剧,作用力比远偏状态和初始状态下大,应力增大,顶部接头处的张力减小、应力减小;对于顶部接头处的弯矩而言,其受顶部浮体偏移的影响较小。当浮体远离触地点时,变化规律与之相反。在动态分析下可看出,立管的贯入深度和管土间接触作用范围较于静态明显增加。

图11 不同偏移状态时的动态响应
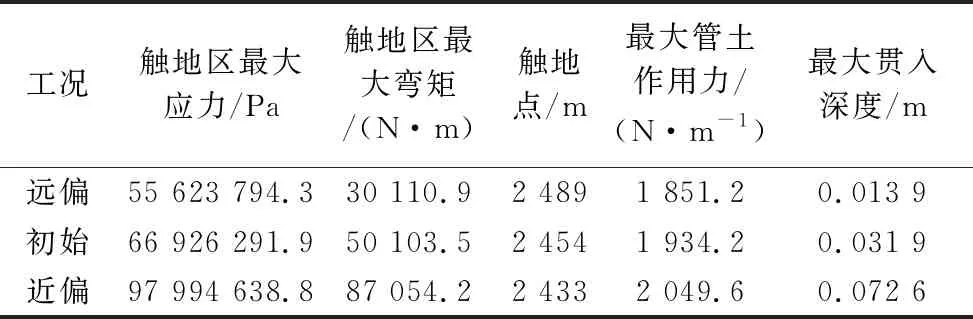
表4 不同偏移状态下立管的动态计算结果
3.2.2 海床土体属性及相关参数影响
海床土体抗剪强度指土体能够承受剪切破坏的极限强度,在一定应力范围内能够用线性函数来近似表达,如式(3),以非线性海床模型为土体模型,该类海床的强度可分为低、中、高强度三种强度的海床模型。为对初始工况下的海床模型对立管触地部分的动态响应进行研究,选择三种强度的海床模型进行比对,相关联土体表面抗剪强度为1.2 kPa、2.6 kPa、3.8 kPa,抗剪强度梯度为0.8 kPa/m、1.25 kPa/m、2 kPa/m。
从图12(a)—(d)及表5可看出,土体抗剪强度对管土相互作用的影响较大,随着土体抗剪强度的增大,立管的有效张力会变小,触地点位置会略微向后移动。土体抗剪强度的变化对管土作用范围的影响较小,但管土作用力随土体抗剪强度的增大显著增加,立管的垂向位移幅值会随着土体抗剪强度的增强而降低,贯入深度越来越浅,越接近海床土体变表面,垂向位移曲线就愈发趋于平坦。土体抗剪强度对立管应及弯矩有着一定的影响,在触地点前一段可看出,土体抗剪强度大的模型立管应力偏大,在立管贯入区域土体强度大的模型应力则偏小,这是由于土体强度较小时,立管的贯入深度较大使得该区立管弯矩增大,导致立管应力增大。

图12 不同抗剪强度时的动态响应
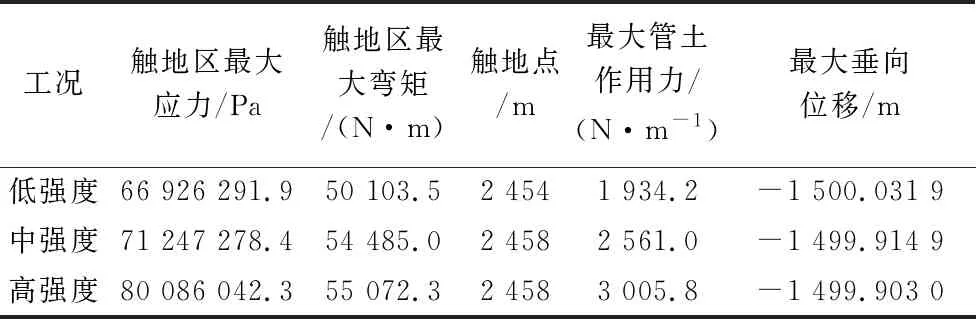
表5 不同海床强度下的动态结果
非线性海床模型的滞回特性受到众多参数的影响,这对立管触地部分的管土相互接触作用有着十分重要的影响,土体表面抗剪强度是海床土体最重要的特性参数,抗剪强度梯度的影响也不可忽视,二者选取的数据参数如表6,N表示数值默认为初始值。

表6 非线性海床土体参数表
从图13(a)—(d)及表7的结果看出,土体表面抗剪强度的变化对与管土作用力的影响显著,随着土体表面抗剪强度的增大,立管触地点的位置会大幅后移。土体表面抗剪强度的增大会导致立管更浅的贯入,随着管长的延伸,立管触地段的贯入趋势会趋于稳定,可看作是立管触地段构型的整体下移。在立管触地点后的弯矩以及应力变化幅值与土体表面抗剪强度的变化呈正比,表明土体抗剪强度的增大会引起立管触地区疲劳损伤增大,触地点的弯矩与应力的变化趋势趋于一致,表明弯矩应力是触地点应力重要组成。

图13 不同土体表面抗剪强度时的动态响应

表7 不同土体表面抗剪强度下的动态结果
从图14(a)—(d)及表8可以看出,立管的触地区的弯矩和应力对抗剪强度梯度的变化不敏感。土体抗剪强度梯度的变化对立管触地的作用范围几乎没有影响,管土作用力随着土体抗剪强度梯度的增大,其数值略微增大,但增幅较小,主要体现在立管触地点附近会相应的增大。抗剪强度梯度的变化对立管触地点位置几乎没有影响,但立管的贯入深度会相应的减小,土体抗剪强度梯度的变化,使得立管贯入段的弯曲度加大,这与土体表面抗剪强度的变化导致的影响有所差别,土体表面抗剪强度的变化引起的立管贯入段的构型较缓。
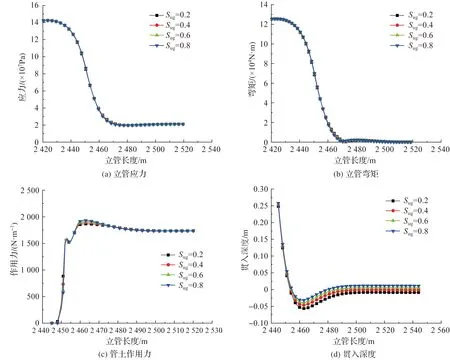
图14 不同抗剪强度梯度时的动态响应
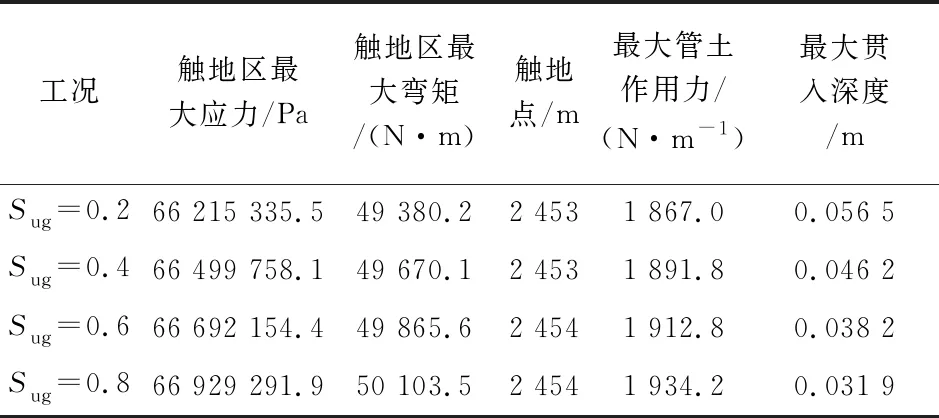
表8 不同抗剪强度梯度下的动态结果
3.3 管内流体的影响
由于立管的特殊功能性,海洋管道被用来输送高压高速的油气资源,不同的内部流体会对管道的形状造成一定的影响,这是由于缓波型柔性立管的特殊布局所导致的。为探究管内流体密度对布置形状的影响。采用控制变量法,保持除密度以外的其他参数不变,对立管在三种管内流体密度(790 kg/m3、950 kg/m3、1 025 kg/m3)下的动力响应结果进行计算。
图15(a)给出了不同情况下立管的形状布置图,可看出随着立管内流体密度的増大,立管逐渐下沉,这是由于缓波型立管主要由浮力段提供浮力来维持波形,当浮力一定时,立管内流体密度增大,使得单位长度的立管湿重增加,势必会引起立管下沉。

图15 不同内流密度时的动态响应
根据图15(b)—(d)可以看出,立管顶端张力同流体密度变化趋势一致,浮力段前半段张力受密度变化的影响较小,后半段张力随着密度的增大稍有降低。管内流体密度对于立管弯矩的影响主要集中在浮力段附近,浮力段前半部随密度的增大而减小,在后半部弯矩随密度的增加而增大。从图15(e)—(f)以及表9可看出,内流密度的增大会造成立管触地点位置前移,立管的贯入深度会相应的增大;但对触地区管土作用力而言,密度的变化对作用力的峰值影响较小,作用力的整体变化趋势基本不受影响。
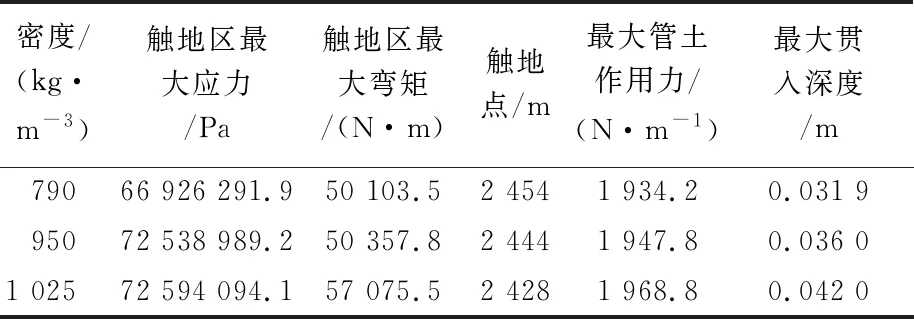
表9 不同密度下的动态结果
管道内部常以一定的速度来输送油气资源,为分析内部流体的流速对置于非线性海床土体上的立管动响应的影响,保持除内部流速之外的各项参数条件不变,设置管道内部流速为0 m/s,1 m/s,3 m/s,10 m/s,15 m/s,对其影响下立管动态分析结果进行比较。
不同流速下立管的分析结果如图16(a)—(d)及表10。不难看出,随着管道内部流速的增大,从0 m/s变化至15 m/s,速度跨度渐渐增大,但立管的有效张力、弯矩、应力对于内部流速的变化不敏感。有效张力的增幅也仅仅是稍微提升。立管的触地点位置对于内部流速的变化未发生改变,对应的立管贯入深度基本没有差别。且立管触地区的管土作用力基本不受其速度变化的影响。总体可认为内部流速度的变化对于立管动力响应的相关结果基本无影响。

图16 不同内流速度时的动态响应

表10 不同内流速的动态结果
4 结 论
基于非线性海床土体模型建立的LWSCR三维数值模型,探讨了浮体偏移、土体模型强度及其相关参数和管内流体对立管触地区管土作用的影响,得到不同条件下的立管的静力分析、动力响应结果。
1)在静态分析中,浮体偏移以及流体密度的变化对立管的构型影响较大,浮体从远偏到近偏,立管的整体波形会变拱,立管的有效张力、管土作用力、贯入深度等会相应增大。
2)在动态分析中,浮体偏移对立管的张力、弯矩、触地点位置、立管贯入深度等有着显著的影响,近点偏移与远点偏移的变化规律相反。立管的应力随着立管长度的分布与张力以及弯矩的变化相关,在顶部接头及触地部分存在极大值,这表明该部分是立管强度破坏的高频区段。可见,浮体偏移是导致立管结构破坏的关键因素,在设计时可选用远偏状态下的最大张力来对缓波形立管的张力进行校准,选用近偏状态下的最大弯曲来对立管的最小弯曲半径进行核验。
3)海床土体强度及土体参数的变化对立管的贯入深度以及立管贯入部的构型影响较大,立管的贯入深度越大,则立管触地区的管土作用力以及弯矩会相应的增大,相应的应力也会受到影响。
4)管道内部流体密度的增加会造成立管张力的增大,越接近顶端增幅越显著,立管触地区的贯入深度和管土作用力与密度的变化呈正相关,立管触地点的弯矩和应力也相应增大。立管的整体动力响应的结果对管道内部流速的变化不敏感,整体的变化趋势趋于一致。
综上,LWSCR在深海开采中的重要性愈发突出,因此在立管设计过程中,需要对其所承受的实际载荷、海床土体以及管内流体属性的选取慎重考虑,这对立管的结构强度以及疲劳寿命具有重要的参考意义。
