小波变换技术在NO质量浓度检测的应用

杨德尚,王 琦,沈德魁,王启昌,张滕成

(1.中国计量大学计量 测试工程学院，浙江 杭州 310018；2.东南大学 能源与环境学院，江苏 南京 210000)

近些年来，我国对于污染气体排放管控越发严格，就NOx的排放指标而言，从2003年我国发布的GB13223—2003《火电厂大气污染排放标准》[1]，再到目前为止已经从650 mg/m3要求限制到50 mg/m3。这表示我国对于污染物的排放要求日益严格[2]，我国已全面进入更加严苛的超低排放改造时期。而电厂烟气污染物(主要为SOx和NOx)浓度检测领域，通常的测量方法是利用差分吸收光谱(DOAS)技术[3]，DOAS技术在20世纪80年代初发展相对成熟，最初应用于大气的气体质量检测方面，在80年代末的时候，已在大气污染检测仪器领域得到了广泛认可[4-5]。在DOAS四十多年的发展过程中，已经实现在多个领域进行探测，工业的烟气监测环境就是其中之一[6]。

目前，DOAS发展迅速，对其系统不断完善，增强了其可靠性，Stutz等[7]对浓度反演方法进行了改进,为了消除光谱的平移、展伸和压缩对测量的影响,采用了线性最小二乘与非线性的Levenberg-Marquardt方法,而摒弃了前人所采用的纯线性算法，这使得测量结果的真实性得到了保证；Ahilleas等[8]提出了一种针对高精细结构光谱的参数反演法，这使得DOAS向红外区扩展有了可能。而在烟气的环境下，考虑到其中的水分和灰尘导致的散射影响，传统DOAS算法中的应用多项式滤波已无法消除Mie散射对气体差分吸收度的影响,气体浓度的反演结果远远偏离真实值[9-11]。汤光华[12-13]等通过短光程DOAS技术，并结合多项式结合小波变换的滤波方法消除了Mie散射对于气体浓度反演结果的影响，以及新的温度补偿算法和线性补偿算法，大大降低了气体反演浓度的误差。李素文等[14]提出一种软阙值小波变换去噪方法，解决实际测量过程中系统噪声与吸收光谱叠加干扰的问题，从而提高了DOAS的测量精度，较好地保留光谱特征信息。梅魏鹏等[15]在针对系统噪声和Mie散射造成的光谱叠加误差现象，提出了小波变换降噪技术，实验通过对Symlets、Daubechies、Coiflet和Bjorthogonal这四种不同的小波函数进行降噪数据分析，最终确定基于rigisure阈值的小波变换降噪可以有效的提高检测精度，虽然滤波后测量得到的浓度值相对误差还存在波动，但是误差的绝对值得到了较大的降低，在剔除掉粗大误差带来的影响之后，能将SO2浓度的准确度控制在1.5%以内。

本文在梅魏鹏等人对SO2浓度研究理论基础上，通过使用小波变换技术对NO差分吸收光谱信号进行变换分解，分析每层中的有效信号进行浓度反演，确定最适的小波函数以及分解层数。该方法无需再将信号进行重构，直接从相应的分解层数上提取有效信号进行浓度反演计算，算法结构简单化；同时也为实际烟气环境下，利用小波变换将NO和SO2两种气体的有效信号分解到不同层上进行浓度反演，防止两种气体相互干扰影响浓度检测的准确性，从而提高了两种气体的检测精确度，为实际烟气光谱数据处理提供了一种分析思路。

1 检测原理

1.1 DOAS浓度检测

DOAS技术是通过将一段具有差分吸收结构的光谱波段加以利用[16-17]，再对其差分吸收光谱强度进行浓度反演，得到待测气体的浓度值；其基本原理是Beer-Lambert吸收定律，如式(1):

I(λ)=I0(λ)exp[-σ(λ)CL]。

(1)

式(1)中：I、I0分别为入射光强和出射光强；λ为波长，nm；σ(λ)为吸收截面，cm2/mol；C为单位体积内吸收物质的分子密度，mol/cm3；L为吸收光程，cm。

将Beer-Lambert公式进行变换，再结合实验室测出待测气体的标准吸收截面，就可求取待测气体浓度，简化为

(2)

其中M为待测气体的摩尔分子质量。

1.2 小波变换技术

小波变换法具有良好的时间局部分析能力，可以在去除差分吸收截面上噪声的同时，保留了光谱的特征成分，适合较为复杂环境下的信号处理提取[18]。小波变换的基本原理是：当收到一个信号，先将它展开成小波的平移和伸缩之和，接着把欲舍弃项的系数去掉或者加以适当的修改，由修改后的小波系数做逆向小波变换得到新的信号[19]。

当一个复杂信号S通过小波变换分解(以3层变换分解为例)，如图1，首先得到的是小波系数高频部分d1和低频部分a1，再对低频部分a1进一步分解成，高频部分d1不再分解。最终复杂信号S可以由最后一层的低频部分加上所有层的高频部分：

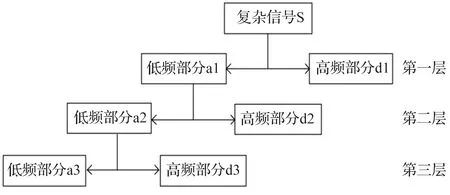
图1 3层小波变换分解示意图

S=a3+d1+d2+d3。

(3)

对一段复杂信号进行小波变换时，所采取的小波函数并不是只有一个，当该信号可以符合相应函数的小波条件，那么说明该函数可以作为小波函数进行变换分解，因此，选取最适合的小波函数及其对应的分解层数是小波变换过程中非常关键的一环。目前对光谱数据信号处理效果较好的小波系主要有：Daubechies(dbN)小波系、Biorthogonal(biorNr.Nd)小波系、Coiflet(coifN)小波系和SymletsA(symN)小波系。接下来将分别对这四种小波系进行实验数据验证，找出最合适的小波函数及其分解层数。

2 NO小波函数对比实验

本实验结合NO气体的紫外吸收光谱范围，确认选取光谱图的200～230 nm范围作为NO差分吸收光谱数据，在30～800 mg/m3的NO质量浓度区间内采集28组不同质量浓度，并保证每组的差分吸收光谱数据采集10次。NO小波函数对比实验所需要的设备有光谱仪、脉冲光源、气体检测池、气体混合池、流量计控制器、6 mm聚四氟乙烯管、NO质量流量计(100 SCCM)、N2质量流量计(1 500 SCCM)、计算机(MATLAB软件)、体积比2%的NO气体和N2填充气体，实验实际搭建如图2。

图2 NO实验装置

首先使用脉冲光源对光谱仪波长进行校准；接着考虑到探测器暗电流的影响，关掉光源或封锁光路，记录探测器暗电流强度；然后打开光源，气体池中充满N2气体，记录参考光强；最后调节N2气体和NO气体的分压阀，通过相应的质量流量计控制流速比，确定待测NO气体的质量浓度值，当气体池内NO质量浓度稳定后，记录通过气体池后的采样光强；同时在气体池中装入待测气体以及填充气体，记录装入的被测气体的分压强、温度。这样可以从参考光强中减去暗电流得到入射光强I0，从采样光强中减去暗电流得到出射光强I，计算出被测气体NO的差分吸收光谱数据。

在MATLAB软件中选取dbN、biorNr.Nd、coifN和symN四种小波系函数分别代入到NO的差分光谱数据当中进行小波变换，将分解成的an,d1,d2，…，dn不同层光谱数据进行分析提取吸收特征值，通过提取出的特征值进行质量浓度反演，计算出预测质量浓度的相对误差，对比出相对误差最小的结果为最优小波函数及其对应的分解层数。

通过以上对NO差分吸收光谱进行了四种小波系函数的小波变换，探索不同小波系函数对于质量浓度反演精度的提升。如何可以准确判定小波函数对于质量浓度反演结果的影响，本文通过不同小波系函数的小波变换后，分别对533.49 mg/m3、302.97 mg/m3、97.77 mg/m3、69.92 mg/m3、32.68 mg/m3的5种待测质量浓度NO差分吸收光谱进行浓度反演，为选出最优的小波系函数，本实验定义参考值曲线拟合度K:

(4)

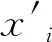
3 NO气体实验结果及分析

3.1 小波分解层数的研究

考虑到db1、bior1和sym1的小波函数特性，在对复杂的NO差分吸收光谱信号进行小波变换之后，各层的信号失真比较严重，无法对其进行有效信号的提取，因此这三种小波函数不在实验研究对象之中。

通过对采集到的NO差分吸收光谱数据分析计算整理后，表1是分别对原始差分光吸收谱信号、db2小波变换、bior2.2小波变换、coif1小波变换、sym2小波变换和sym3小波变换后针对不同分解层进行质量浓度反演计算出的参数值K。

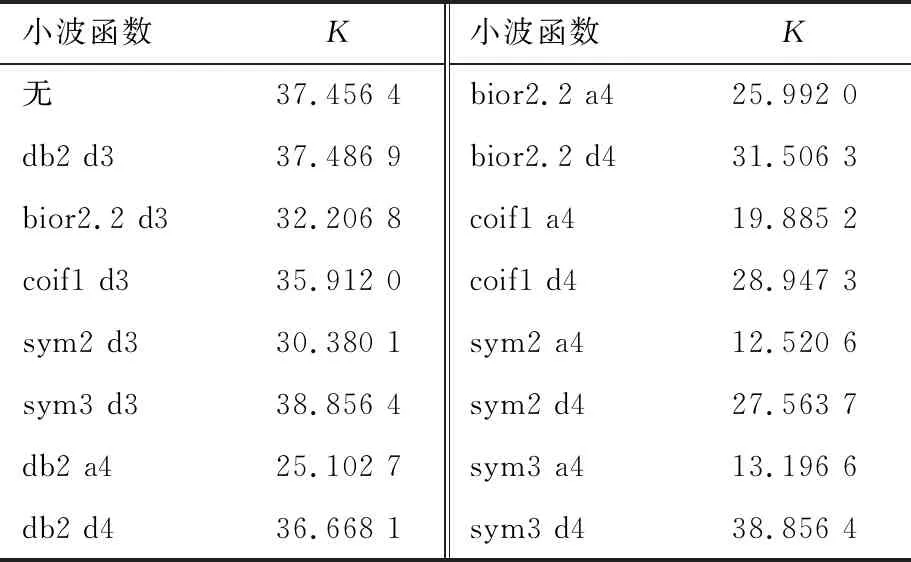
表1 不同分解层下小波函数的参数K

从表1的数据中可以看出，原始差分光吸收谱信号未经小波函数变换得出的K值为37.456 4，而经过db2、bior2.2、coif1、sym2和sym3的5个小波函数变换分解下，5种小波函数的d3层K值与原始差分吸收光谱信号的K值相近，如表1K值都保持在30以上;有些甚至不如原始差分吸收光谱信号直接浓度反演获取的拟合曲线，这表示在d3层上NO的有效特征值较少，不适合进行特征值提取以及反演质量浓度；从另一个方面来看，d3层的K值越大表示反演质量浓度与真实的待测质量浓度存在较大误差，无法实现精准预测NO待测气体的质量浓度，从而可以看出，在这四种小波系的d3层分解上，还有NO气体的有效信号较少，无法进行质量浓度反演预测。相反，在四种小波系函数进行的小波变换分解的第4层上，a4和d4的K值与原始差分光吸收谱信号K值相比表现相对良好，其中a4的K值相对较小，质量浓度反演曲线的拟合效果更好一些。接下来也将进一步对dbN、biorNr.Nd、coifN和symN四种小波函数的a4和d4层进行分析，验证差分吸收光谱信号在小波变换分解到a4层的有效信号更为集中，以及选取质量浓度反演曲线误差最小的小波函数。

3.2 小波种类的研究

如表2和表3，分别是dbN、biorNr.Nd、coifN和symN 4种小波函数在a4和d4层进行质量浓度反演后，通过选定的533.49 mg/m3、302.97 mg/m3、97.77 mg/m3、69.92 mg/m3、32.68 mg/m3这5种待测质量浓度代入到公式(4)中求取的拟合曲线参数K，最终通过对K值进行分析来判定最佳的小波函数以及分解层数。

从表2和表3的数据分析可以看出，差分吸收光谱信号在四种小波函数变换分解后a4层的K值从整体来看比d4的K值要低很多，这进一步验证了上面提出的观点，a4层NO气体的有效信号更为集中，这利于接下来的质量浓度反演并可以进一步提高预测的精准度。

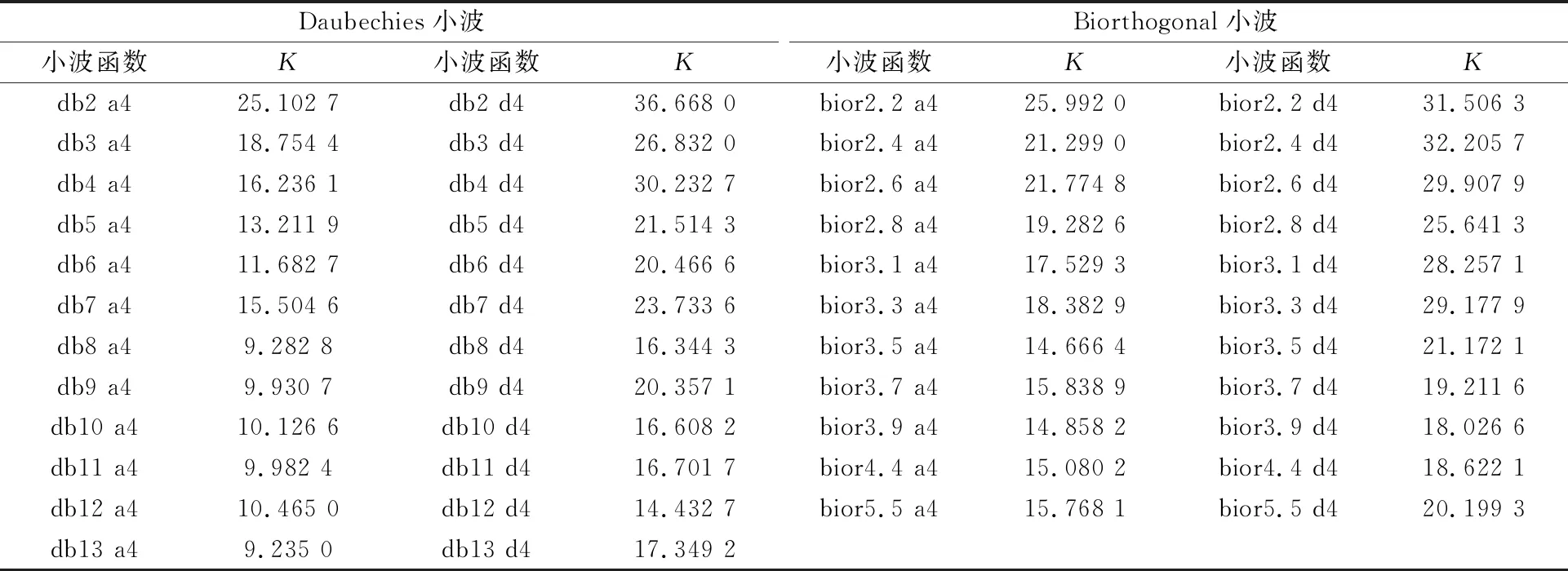
表2 dbN和biorN小波函数下的参数K

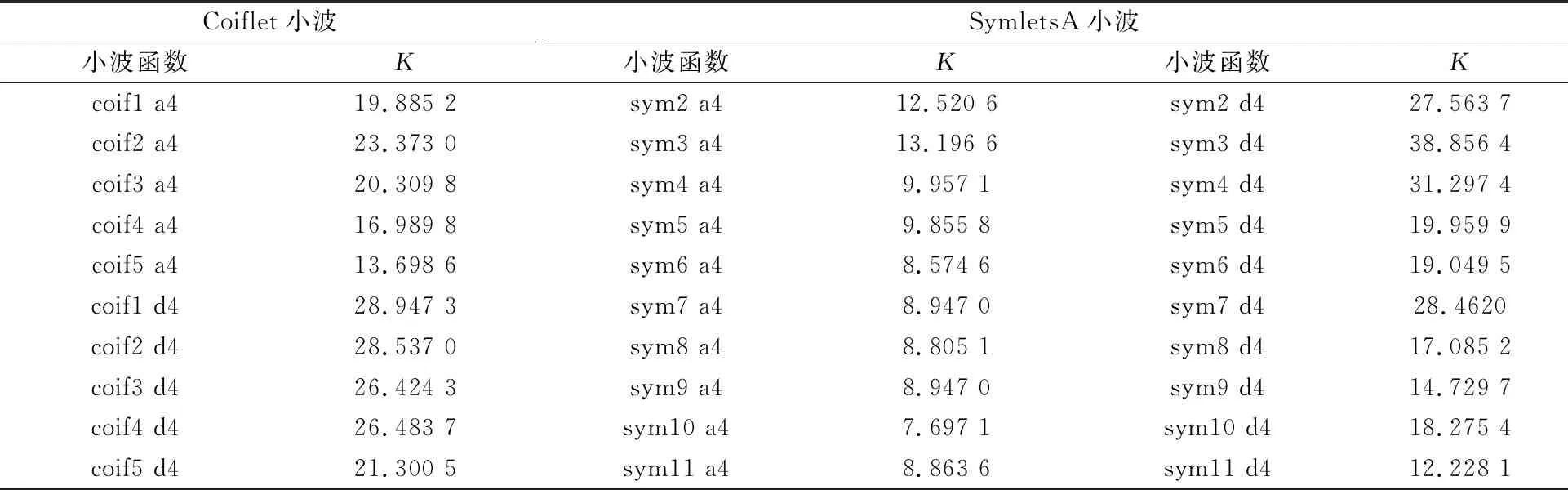
表3 coifN和symN小波函数下的参数K

图3到图6是四种小波函数在a4和d4层的参数K值变化曲线，可以更直观看见四种小波函数的a4的K值变化趋势均在d4的K值曲线之下，其中dbN小波函数在db8 a4后对于NO差分吸收光谱的小波变换分解不再随着N值变大而有较大提升预测拟合曲线的稳定，最终K值保持在9.2左右，这与biorN a4层和symN a4层的K值变化趋势相似，分别出现在bior3.5和sym6，相应的K值稳定在14.7和8.6左右，而coifN a4层的K值最低点出现在coif5处，对应的K值为13.7。但是总体来看，四种小波函数的参数K值相比之下，小波函数变换之后质量浓度反演结果效果较好的情况是db8和sym6这两个小波函数，前者参数K值为9.2828，后者为8.5746。将这两个小波函数在新采集到的数据下进行实验误差验证后，所得的结果数据如图7和表4所示，差分吸收光谱数据经sym6和db8这两个小波函数变换分解后所得到的反演质量浓度，与待测质量浓度对比，相应的质量浓度相对误差均不超过7.8%，预测质量浓度准确性较高，符合实验预期。

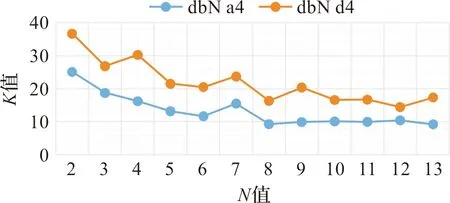
图3 dbN的K值变化曲线

图4 biorN的K值变化曲线

图5 coifN的K值变化曲线

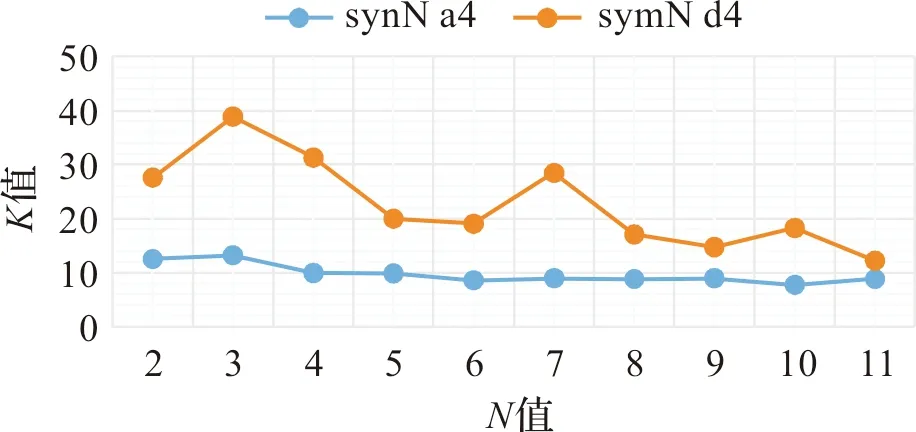
图6 symN的K值变化曲线

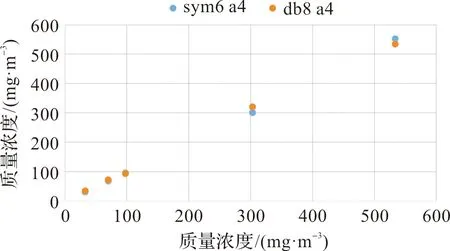
图7 sym6和bd8的实验误差验证

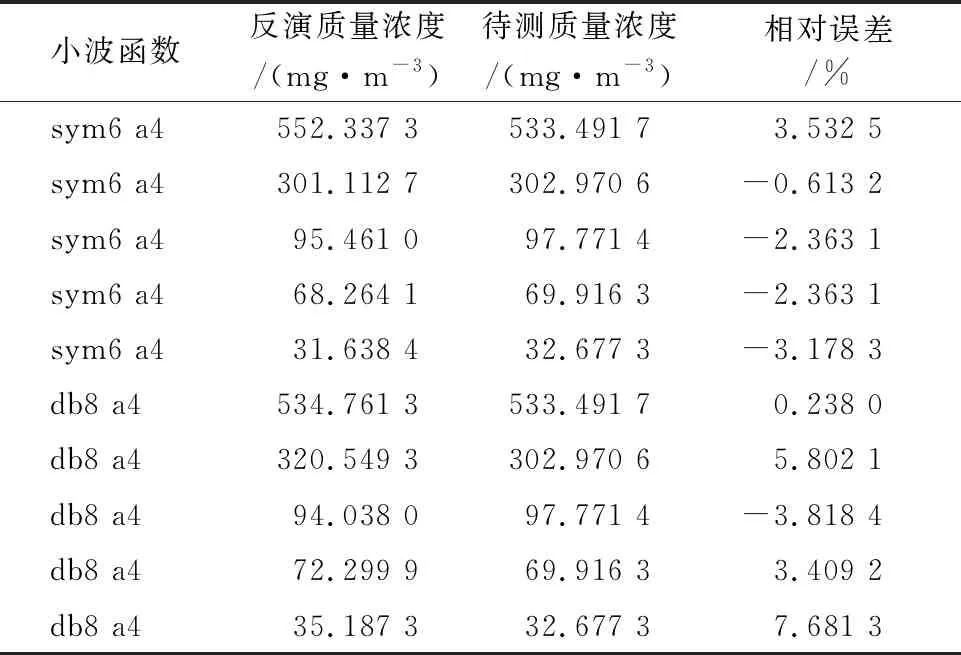
表4 sym6和bd8的实验误差验证数据

4 结 论

本文通过NO小波函数对比实验，将各质量浓度下的相对误差结合K值数据进行的分析，最终得到以下结论。

1)可以很明显的看出四种小波函数系中，对于差分吸收光谱数据处理效果最好的小波函数是sym6，其次是db8，也确定了NO的有效信号主要集中在小波变换的a4层。

2)在实验环境下这两个小波函数处理后进行的质量浓度反演，其所有的相对误差都未超过7.8%，其中sym6小波函数处理后的反演质量浓度误差相对稳定，最大误差为3.6%，很好地提升了NO的质量浓度检测精度。

3)同时，如何在NO和SO2混合气体中准确快速的同时检测两种气体浓度，本次试验提供了一种可行的思路，即选取合适的小波函数对混合气体的差分吸收光谱数据进行变换分解，将NO和SO2两种气体的有效信号分别分解到不同的小波层数上。本文主要针对NO气体进行了分析实验，下一步将对SO2进行实验分析，以实现将两种气体分解到不同小波层数上，依次进行有效信号提取反演质量浓度，解决了两种气体在吸收光谱上相互重叠干扰的问题。