直升机旋翼动平衡检测及优化算法研究
2023-01-11裘燕青钟宇民毛邦宁
邵 宸,裘燕青,钟宇民,毛邦宁
(中国计量大学 光学与电子科技学院,浙江 杭州 310018)
直升机旋翼的振动是影响直升机安全性能和驾驶舒适度的重要因素,而导致旋翼振动过大的原因往往是旋翼的质量分布不平衡,因此需要及时对旋翼进行例行动平衡检测及重心配平调整。
目前用于旋翼动平衡检测技术的设备基本依赖进口,其中主要的技术难点在于旋翼的振动信号提取与分析方法。由于直升机旋翼工作状态和工作环境复杂多变,它的振动信号包含着发动机、环境、气流等造成的多种复杂噪声。而传统的单纯基于傅里叶变换的频谱分析方法很难有效地提取出单独的旋翼振动信号,从而影响到后续振动幅值和相位判别的准确性。
阶比分析是一种针对于旋转机械的信号分析方法[1,2]。其中最初的阶比分析方法是在等时间间隔采样后,利用快速傅里叶变换算法(fast Fourier transform,FFT)来进行计算的阶比分析法。但是其在分析不稳定转速的旋转机械的振动信号时,会出现频谱泄漏的状况[3],且在低转速时,阶比分辨率低下。
为解决这些问题,有人提出了“跟踪算法”,通过跟踪转速的快慢变化,将振动信号进行等角度重采样过程,使之采样频率与旋转速度的变化保持一致[4]。但即便基于等角度重采样的FFT阶比分析法,在有多个独立运动的转轴时,依然会产生问题交叉阶比问题[5-7],导致数据失真。
在1993年,Vold-Kalman和Leuridan提出了基于Kalman滤波器的第一代跟踪算法,实现了可以分析时变阶比谱的功能[8]。然后又在1997年,他们提出了第二代基于Kalman滤波器的跟踪算法,在拥有高分辨率、高转换率的同时,能同时提取多个阶比,且能准确分离交叉阶比与邻近阶比的Vold-Kalman跟踪滤波算法[9]。
本文设计了一种基于第二代Vold-Kalman跟踪的直升机旋翼动平衡检测算法及相应的信号采集系统。信号采集系统能够快速准确地采集旋翼的振动信号与转速信号。随后将采集的振动信号进行等角度重采样,再利用重采样后的信号进行基于FFT的信号分析与基于Vold-Kalman跟踪滤波的信号分析。文中对这两种不同的信号分析方法得出的结果进行了多方面的对比,发现基于Vold-Kalman跟踪滤波的信号分析方法明显优于另一种,且满足动平衡检测仪器的精度要求,在直升机旋翼动平衡检测领域有着广阔的应用前景。
1 整体设计方案
1.1 动平衡检测原理
当直升机旋翼的质心偏离转轴中心时,基频为旋转频率的谐波频率成分会通过桨毂传递到机体,使得机体原有的振动频率增加了与旋翼转动频率及幅值相关的成分。因此通过振动传感器采集直升机的振动信号,结合光电转速传感器获取旋翼的转速和位置,再通过算法进行信号处理与分析后,可以提取出旋翼不平衡的相位与幅值信息。最后根据识别出来的旋翼不平衡程度,利用标准的配平片进行配平调整来实现旋翼的动平衡。
1.2 整体设计方案
整体设计方案包括两大部分,一是直升机旋翼振动信号采集系统,二是通过滤波算法对采集到的旋翼振动信号进行的信号处理与分析系统。
直升机旋翼振动信号采集系统包括信号采集硬件系统、信号采集程序、数据可视化终端。其中硬件系统采用ARM芯片作为信号采集电路主控模块。
信号处理与分析系统主要由Vold-Kalman跟踪滤波算法的程序实现。该算法程序采用MATLAB作为开发环境,其中的主要步骤包括:基于转速脉冲信号的周期截取,周期信号的等角度重采样,Vold-Kalman跟踪滤波算法,基于FFT的信号幅值与相位计算等。
2 信号采集系统设计
2.1 信号采集硬件设计
信号采集硬件系统由光电转速传感器、光电振动传感器、显示系统、电池系统、ARM控制系统所构成,如图1。
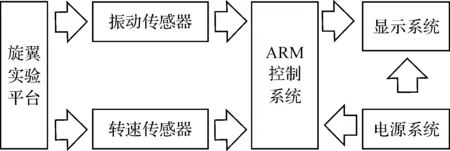
图1 硬件框图
2.2 信号采集流程
信号采集以参考桨叶为基准,利用光电转速传感器接收到的触发信号为采样周期,利用振动传感器采集相应的振动信号。
振动信号和转速信号通过ARM芯片的预处理后,利用高速USB将数据传输至微型工控机。数据采集程序流程如图2。

图2 信号采集流程图
3 算法设计及程序实现
3.1 算法设计
振动传感器采集而来的原始振动信号构成极为复杂,包含有来自于发动机、减速器、旋翼等多个振源的混合振动信号。而在旋翼动不平衡检测时仅需要旋翼的振动信号,因此需要滤波算法从复杂的信号中提取出单独的旋翼振动信号。
为实现此目的,故对每一个整周期信号进行单独分析。本文首先将传入的原始振动信号根据转速脉冲信号的上升沿截取整周期,而每个整周期信号就是旋翼旋转一周的振动信号,然后再针对每一整周期信号进行处理。
由于直升机旋翼是旋转机械,而旋转机械运动时,其转速严格来说是波动的。直接的FFT频谱分析是主要针对于稳态信号的方法,当其被用于进行非平稳信号的分析时,可能会出现频率混叠和能量泄漏,故采用阶比分析技术,可更好地对旋转机械的信号进行分析。
阶比分析技术的关键在于对信号的等角度采样,即对初始的等时间间隔采样信号进行等角度重采样。为此需要重构新的采样时刻,首先为减少噪声干扰,对初始信号进行FFT,确认幅值较高的频率范围,对初始信号进行带通滤波来获得阶比频率信号。然后再对这个信号进行等角度重采样。
等角度重采样后的振动信号可以确保为一个完整的整周期的信号,随后对整周期信号进行Vold-Kalman跟踪滤波算法,它适用于旋转机械的信号分析,且分辨率高,能有效地从初始信号中提取出旋翼振动信号。
然后再次对提取出来的旋翼振动信号进行FFT,其中的第二个点便代表着旋翼旋转一周对应的相位与幅值,用于进行旋翼动不平衡分析。整体的算法流程图如图3。
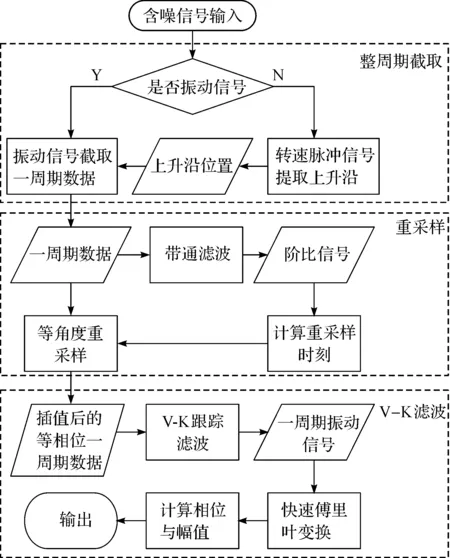
图3 Vold-Kalman滤波算法程序流程图
3.2 Vold-Kalman滤波算法原理
Vold-Kalman滤波算法由状态方程和观测方程共同表示,本文中采用的是第二代Vold-Kalman跟踪滤波。
阶比的本质是一个幅值和频率随时钟在改变的正弦函数,其定义是指参考桨叶每旋转一圈所产生的循环振动次数。因此阶比信号可以被描述为幅值和载波的乘积[10-12]:
(1)
式(1)中,x(t)为被跟踪的阶比分量;k为基准频率,定义为被跟踪的阶比;ak(t)为复包络,显示了阶比幅值的变化,a-k(t)是ak(t)的复共轭;θk(t)为载波,定义为

(2)

Vold-Kalman滤波器是由状态方程和观测方程共同表示的[13]。而第二代Vold-Kalman跟踪滤波的状态方程为
▽sak(n)=ε(n)。
(3)
式(3)中,▽为不同的算子,s为确定的阶数,ε(n)为非一致项。
本文给定的阶数为二阶,故该状态方程的二阶多项式为
▽2ak(n)=ak(n)-2ak(n+1)+ak(n+2)=ε(n)。
(4)
在只提取单个阶比成分的情况下,第二代Vold-Kalman跟踪滤波的观测方程为
y(n)=x(n)θ(n)+ξ(n)。
(5)
式(5)中,y(n)为实际测量数据,x(n)为被跟踪的阶比分量,ζ(n)为非跟踪的阶比和随机信号噪声。
使用单轴阶比的求解方法即可求出经第二代Vold-Kalman滤波器后的所需信号。
4 实验结果
实验测试了某型直升机的主旋翼动平衡数据,在主旋翼转速稳定后,连续进行了4次测试,每次测试数据的采集时长是10 s,采样率为8 kHz。
将通过直升机旋翼振动信号采集装置采集的4组原始数据输入上述的Vold-Kalman滤波跟踪算法程序中。以1组原始数据举例,如图4,其中子图像(a)为振动信号采集器采集到的信号,(b)为转速传感器采集到的信号。

图4 1组原始振动数据
4.1 基于快速傅里叶变换的信号分析
为了与Vold-Kalman跟踪滤波进行对比,等角度重采样之后,首先采用基于FFT的振动幅值、相位提取算法对数据进行分析,等角度重采样后,1个周期数据如图5。

图5 经等角度重采样1周期信号
随后将总计4组每组分别48个周期不同原始信号进行FFT分析,相位在[-π,π]区间内分布直方图,如图6。
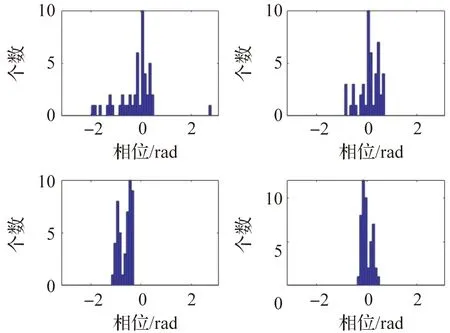
图6 FFT分析相位直方图
由图6的相位直方图可知,基于FFT分析后,其振动信号的相位分布和高斯分布差距较大,甚至存在多峰的现象,计算结果置信度存疑。
为验证数据的收敛性,将每组数据进行平均,并将不同平均次数的每组数据进行FFT,计算不同平均次数的相位与幅值,相位结果如图7,幅值结果如图8。
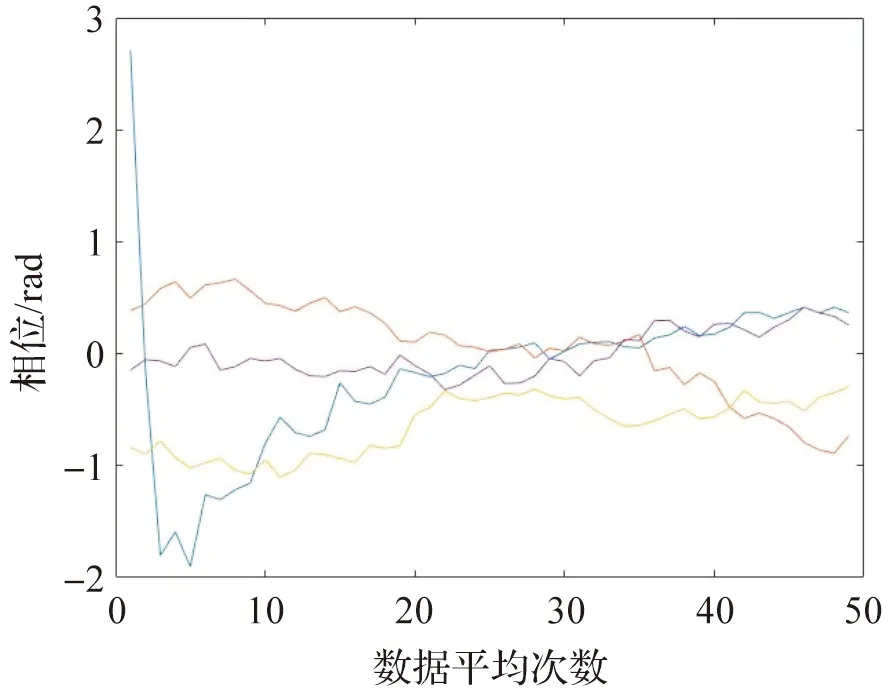
图7 FFT分析不同平均次数相位图

图8 FFT分析不同平均次数幅值图
由图7的相位图可看出,基于FFT的信号分析在低平均次数时,4组数据的相位精度收敛性极差。因为收敛曲线基本在数十次平均之后就已经进入收敛状态,下面用收敛曲线的最后5个数据波动作为数据处理的波动精度。FFT处理的结果,其相位精度也只收敛于±0.55 rad。
同理,由图8的幅值图可看出,4组数据的幅值精度收敛性也不好,在最大平均次数时,其幅值精度收敛于±0.000 508 MPS。
4.2 基于Vold-Kalman滤波的信号分析
根据3.1的算法将4组原始数据通过等时间间隔采样、等角度重采样、Vold-Kalman跟踪滤波等过程后,得出的1个周期的振动信号,如图9。
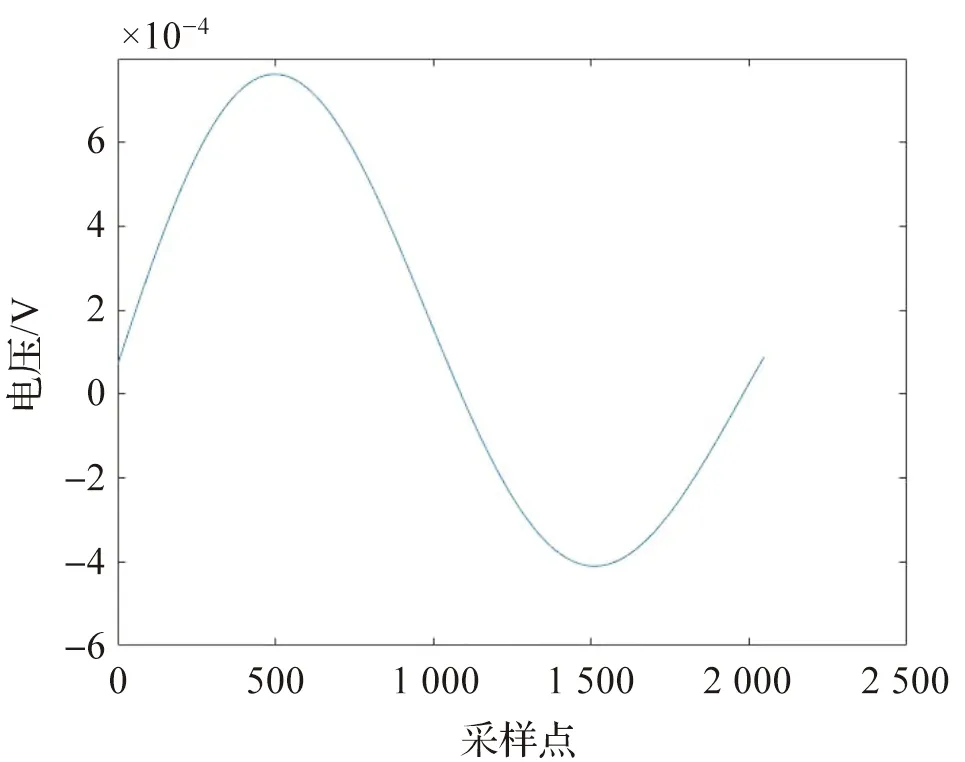
图9 重采样的1周期数据经V-K滤波后
计算相位与幅值,得出4组处理后的数据。4组不同数据计算得出的相位在[-π,π]区间内分布的直方图,如图10。
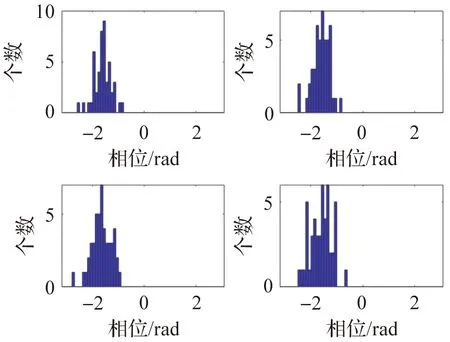
图10 V-K滤波相位直方图
由图10可看出,经V-K跟踪滤波后的信号相位近似于高斯分布,分布重心位置比较一致,说明这是有效的结果。
同理,为验证数据的收敛性,将每组经滤波后数据进行平均,并将不同平均次数的每组数据进行FFT,计算其基频的相位与幅值。每组数据中不同平均次数的相位与幅值,相位结果如图11,幅值结果如图12。

图11 V-K滤波不同平均次数相位图
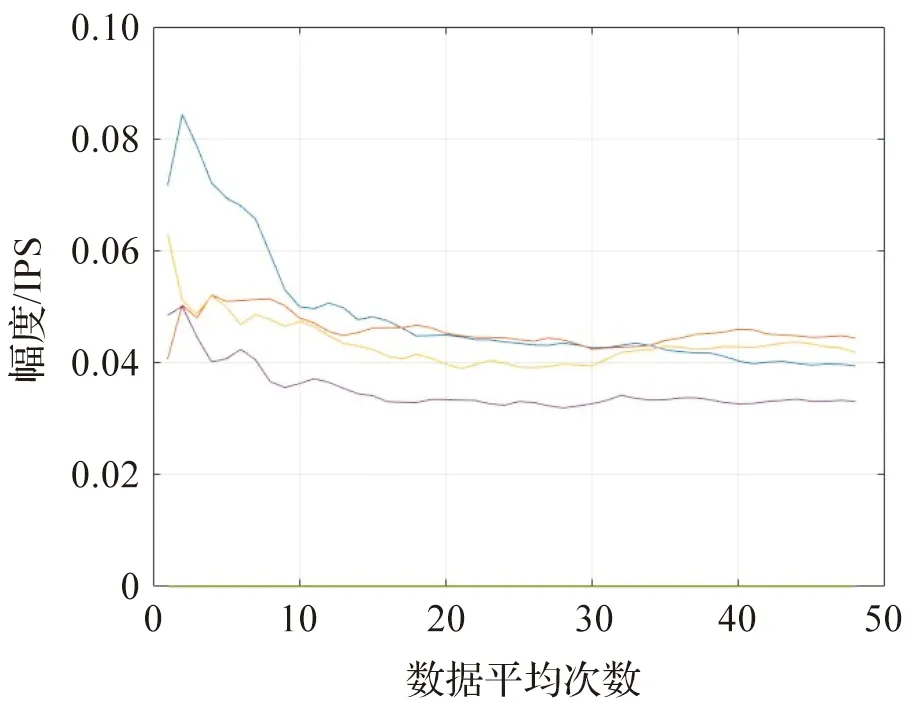
图12 V-K滤波不同平均次数幅值图
将图7与图11进行比对,发现相较于基于FFT的信号分析方法,基于V-K跟踪滤波的信号分析方法的信号的相位收敛的更快,且收敛精度更高。在收敛曲线的最后5个数据波动时,其收敛精度达到了±0.02 rad,远超于相同平均次数的基于FFT的信号分析方法所获得的±0.55 rad的精度。旋翼振动检测要求的相位精度为±0.26 rad,经V-K跟踪滤波处理后的信号符合检测精度的要求。
同样,将图8与图12进行比对,也可发现经V-K跟踪滤波处理后的信号幅值的收敛性很好,在收敛曲线的最后5个数据波动时,其幅值收敛精度达到了±0.000 178 MPS。既超过了基于FFT的信号分析方法的±0.000 508 MPS,也达到了振动检测的幅值精度要求±0.000 254 MPS。
5 结 论
本文提出了一种基于Vold-Kalman跟踪滤波的算法并制作了相应的直升机旋翼振动采集装置。实验结果表明,Vold-Kalman跟踪滤波算法能够从含有多种噪声的旋翼振动原始信号中,准确的分离出了单独的旋翼振动信号,并且相位精度达到了±0.02 rad,振动幅值精度达到了±0.000 178 MPS,满足动平衡测量对幅值和相位的精度要求。
