高弗劳德数条件下攻角对通气超空化流动影响

2023-01-11王宜菲党建军黄闯许海雨左振浩

西北工业大学学报 2022年6期

王宜菲,党建军,黄闯,许海雨,左振浩

(西北工业大学航海学院,陕西西安 710072)

超高速航行器通过人工通气生成的大尺度覆体空泡阻碍了航行器与水接触，实现航行器航行阻力显著减小，航行速度得以大幅提升[1]。不同于常规航行器，超高速航行器的流体动力特性取决于超空泡流型及泡体相对位置关系。航行器的攻角不仅会引起空泡轴线偏移，还会改变形态特征[2]。为了准确预测超空泡流型，需要针对超高速航行器的巡航工况，研究攻角对高弗劳德数条件下超空泡流型的影响规律。

国内外研究学者针对攻角引起超空泡形变问题展开了大量的研究。Mokhtarzadeh[3]指出空化器相对来流存在攻角时，空化器承受来流作用的升力，来流受到影响并导致空泡轴线沿该升力反方向偏移。张宇文等[4]基于动量定理分析了单空化器攻角引起的超空泡轴向偏移，总结了超空泡轴线的无因次形变高度的计算公式。超空泡形成包括2种方式：①通入不凝气体的通气超空泡；②高速汽化形成的自然超空泡[5]。刘喜燕等[6]在水洞试验中研究了人工通气超空泡航行体连续变攻角条件下超空泡形态变化，指出攻角变化产生的扰动与超空泡形态改变延迟时间正相关。Lü等[7]开展了低速通气空泡流动非定常特性研究，指出攻角影响通气空泡的流动结构，加剧了其非对称性。Wang等[8]采用CFD的方法，揭示了低速条件下通气超空泡尾流结构特性，指出无攻角时超空泡尾部双涡中心上卷，攻角存在时双涡中心下卷。Liu等[9]将试验与数值仿真相结合，研究发现随着攻角增大，低速通气超空泡迎流面长度减小，背流面超空泡变厚，长度不变。低弗劳德数工况下，通气超空泡的泄气方式主要是双涡管泄气，而超空泡航行器的航速较高时，通气超空泡的泄气方式为回射流泄气。

超空泡航行器的实际工况具有航速高、弗劳德数大等特点，通气超空泡的空泡流型和泄气模式不同于低弗劳德数工况，有必要在高弗劳德数条件下研究航行器攻角对通气超空化流动特性的影响。贾清泉[10]针对高弗劳德数条件下航行器自然超空泡形态进行研究，指出随攻角增大，空泡形态上下分布均匀性变差；栗夫园等[11]发现在大攻角自然空化条件下超空泡会发生明显变形并对航行体的沾湿状态有显著影响。然而，不同于自然超空泡，通气超空泡内部存在压力梯度和气流涡旋，使得自然超空化流动的相关结论不能直接用于指导超空泡航行器的工程实践。

综上所述，从公开发表文献来看，国内外关于攻角对超空化影响的研究主要集中于低速通气空化和自然空化等方面。关于攻角对高速通气超空泡形态及流动特性影响的研究很少，不能准确预测通气空泡流型。本文基于分相流模型和SSTk-ω湍流模型，建立可压缩通气超空化流动的高精度数值计算模型，在系列攻角变化范围内，研究了攻角对通气超空泡形变的影响特性，构建了超空泡中心线与攻角的数学描述，分析了通气超空泡气体流动结构，并对空泡形态变化的作用机理进行了剖析。

1 数值计算控制方程

1.1 基本控制方程

多相流模型包含均质平衡流模型和分相流模型，依据通气超空化水洞试验结果可知，超空泡流动存在明显的气/液掺混，相间作用强烈，分相流模型更适用于此情况。此外，Cao等[12]指出分相流模型在通气超空化上具有更高的计算精度。因此，本文采用分相流模型作为多相流模型建立通气超空化数值模型。

通气介质为常温可压缩空气,其温度与环境水温相同,忽略了因超空化流动而引起的温度变化,因而控制方程中忽略了能量方程。气体密度由泡内压力决定,即ρ=pc/(RgT),pc为泡内气体压力,Rg为气体常数,T为恒温。控制方程涉及连续性方程、动量方程及体积分数方程。

1) 连续性方程

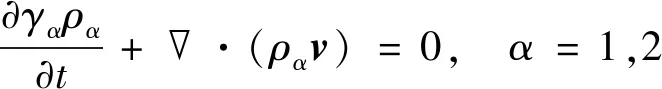
(1)

式中:γα为α相(1为水相,2为气相)的体积分数;ρα为α相的密度;v为流体微元的速度矢量;t为时间。

2) 动量方程

(2)

式中:p为静压;μα为流体微元的动力黏度;g为重力加速度；M为两相间作用力。

3) 体积分数方程

∑α·(γαUα)=0,α=1,2

(3)

1.2 湍流模型

孙鹏[13]指出基于Baseline(BSL)k-ω模型的SST湍流模型综合了k-ω和k-ε模型的优点,考虑湍流的剪切应力传输,可以更加精确地预测流动开始和逆压梯度条件下引起的流体分离。超空泡流场的流动分离导致其湍流强度剧烈,且尾部闭合区存在压力驻点,伴随有逆压梯度,针对以上特点本文选择SSTk-ω湍流模型,基本方程为

式中:k为湍流动能；ρ为密度;ω为湍流频率;Pk为湍流生成率;σk3,σω2,σω3,α3,β3和β′为模型常数。

式中:ν为运动黏度;y为到最近壁面的距离。

1.3 空化模型

空化模型采用基于Rayleigh-Plesset方程的Singhal空化模型,该模型将流场的密度变化与气泡运动联系起来,通过球形空泡生成和破灭过程的数学分析方法,描述了液体中空泡的增长。

具体方程如下

(9)

式中:RB为气泡半径;pc为气泡内压力;p为静压；S为表面张力系数。

若忽略二次项和表面张力项,(9)式可简化为

(10)

则气泡体积变化率为

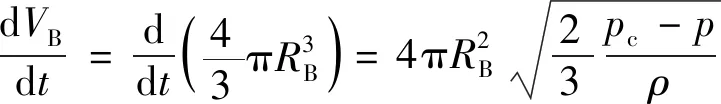
(11)

气泡的质量变化率为

(12)

假设单位体积内有NB个气泡,则体积分数可表示为

(13)

故单位体积内总的质量运输率为

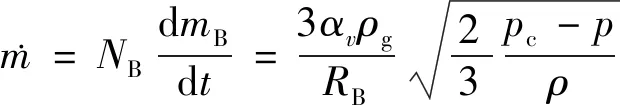
(14)

上述公式是假设气泡增长即汽化时得到的,当气泡凝结时可得到(15)式

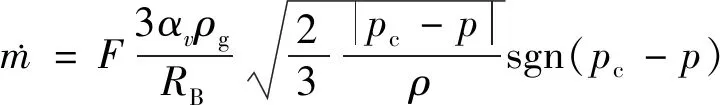
(15)

式中:F为经验常数。

(15)式表征汽化时需要进一步修正,修正后方程为

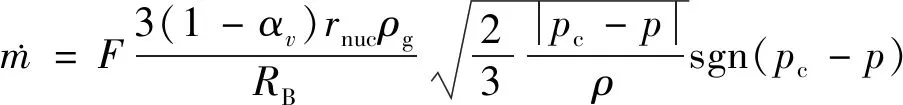
(16)

综合(15)式和(16)式,可得凝结项和汽化项分别为

式中:RB=10-6m;rnuc=5×10-5;Fv=50;Fc=0.01。

Singhal空化模型中的相变率由Rayleigh-Plesset方程得出。

2 数值计算模型

2.1 物理模型

参考某型超高速航行器外形布局[14]获得物理模型,航行器由圆盘空化器、通气装置、航行器锥段、航行器柱段、尾喷管组成。航行器全长为空化器直径的43.2倍。

2.2 计算域及边界条件

计算域如图1所示,左侧边界条件为速度入口,右侧边界条件为压力出口,通气装置边界条件为质量流量入口,通入常温可压缩空气。

速度入口来流速度80 m/s,弗劳德数Fr=147.54,Fr定义如(19)式所示

(19)

式中:V为来流速度,m/s;g为重力加速度,m/s2;dn为空化器直径,m。

压力出口的压力为绝压200 kPa,通气装置的通气率Cq=0.353,Cq的定义为

(20)

式中:Q为超空泡气体体积流量,m3/s;V为来流速度,m/s。

根据边界条件可确定自然空化数σv=0.061 8,σv定义如(21)式所示

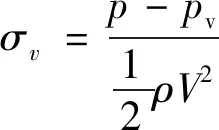
(21)

式中:p为静压,Pa;pv为来流介质的饱和蒸汽压,Pa;ρ为来流介质的密度,kg/m3;V为来流速度,m/s。

通气空化数σc定义如(22)式所示

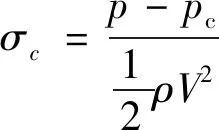
(22)

式中:pc为泡内气体压力,Pa。

许海雨等[15]指出,流域径向尺度至少为理论最大空泡直径的54倍时,高弗劳德数通气超空泡数值模拟结果与流域径向尺度无关。因此,确定流域径向尺度为155dn。图1为详细边界条件设置,其中,攻角α为航行器体轴与来流速度的夹角。

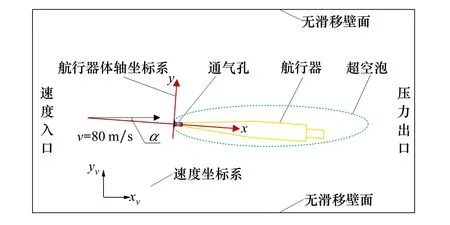
图1 计算域及边界条件

2.3 网格划分

通气超空泡在生成以及发展的过程中,由于尾部闭合区回射流会引起剧烈的气、液两相动量交换,网格的精细化程度影响通气超空化流动及超空泡流型。因此,进行结构化网格划分时,将65%以上的网格集中于通气超空化区域,如图2所示。

为排除网格数量对数值计算结果的影响,分别取58万,116万,232万的计算域网格进行验证计算。58万网格与116万网格相比,超空泡最大长度计算偏差约为4.8%,超空泡最大直径计算偏差为2.5%;116万网格与232万网格的空泡计算结果一致。考虑到有限的计算资源,确定计算域划分网格数量为116万。

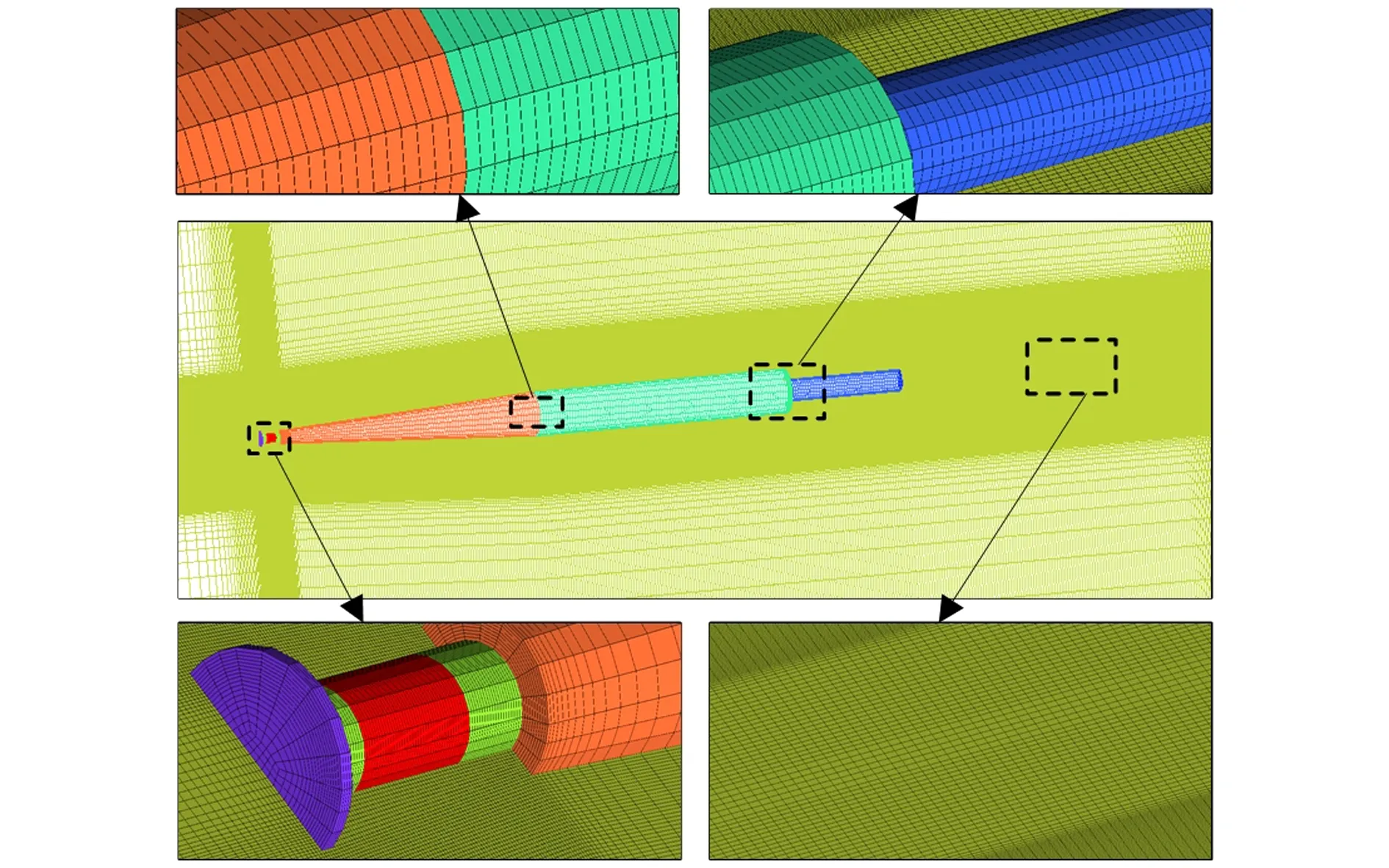
图2 网格分布情况

3 数值仿真与结果分析

3.1 模型验证

依托西北工业大学高速水洞试验室,在弗劳德数为24.8、工作压力70 kPa条件下对细长杆支撑的圆盘空化器开展了通气超空化试验,获得了通气率分别为0.77和1.25条件下的超空泡流型。针对水洞试验工况开展通气超空化流场仿真,仿真结果与试验结果对比如图3所示。

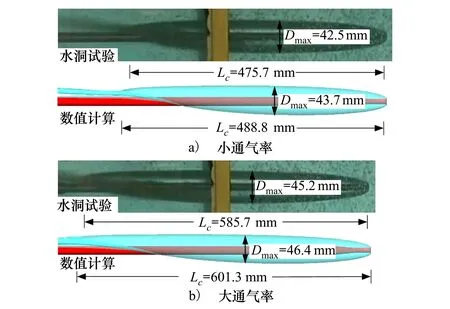
图3 不同通气率下数值仿真与水洞试验超空泡形态对比

小通气率条件下,仿真超空泡最大截面半径与水洞试验相比偏差约为2.82%,长度偏差约为2.75%;大通气率条件下,超空泡最大截面半径的偏差约为2.65%,长度偏差约为2.66%,表明数值模型可用于预测通气超空泡流动。

水洞中试验的水流速度一般不大于20 m/s,为了对高速通气超空化数值模拟结果进行校验,采用Logvinovich[16]通过量纲分析和试验研究建立的泄气率半经验公式进行验模,如(23)式所示

(23)

式中,γ为经验系数,约为0.01～0.02,取0.015;Sc为空泡最大截面面积;V∞为航行器航行速度;σv为自然空化数;σc为通气空化数。

根据理论公式,设置5组仿真工况对比空化数与通气率的关系。仿真结果与经验公式的误差在5%以内,表明本文所建立的高弗劳德数通气超空化数值计算模型可用于通气超空化仿真研究。

3.2 数值计算结果

超空泡航行器的流体动力特性取决于泡/体位置耦合关系,攻角导致超空泡形态发生显著形变。为了获得因攻角增加导致的泡/体位置耦合关系的变化特性,以航行器体坐标系(见图1)代替来流速度方向作为基准,研究超空泡在y轴方向上的形变量,以获得在系列攻角变化范围内泡/体之间的位置变化特性。

3.2.1 高弗劳德数下通气超空泡形态特征研究

为了研究攻角对通气超空泡流型的影响特性,在保持通气率Cq=0.353、弗劳德数Fr=147.54不变的情况下,对大范围系列攻角(α=0°～1.0°)下的通气超空化流动开展了数值模拟研究。以α=0°,0.4°,1.0°为例,不同攻角的超空泡形态如图4所示。

图4 不同攻角下航行器空泡形态

空泡形态以气相体积分数0.5作为空泡轮廓面,为表示回射流现象,给出超空泡尾部在纵对称面上的密度云图。从密度分布特性可知,超空泡闭合区附近的水在尾部压力恢复区的高逆压梯度作用下反向流动进入空泡体内,气/水混合物射流主要位于空泡中心区域,并且在反向流动中水相逐渐向径向扩散。

由图4可知攻角的增加导致通气超空泡流型产生形变,整体发生偏移。为了定量描述攻角对超空泡流型的影响,图5给出了不同攻角下通气超空泡在xoy面上的空泡轮廓曲线,其中包含带攻角的超空泡轮廓轴向偏移简化示意,定义y(x)为空泡中心线(紫线所示)纵向形变高度,纵轴使用空化器直径dn无量纲化处理,横轴使用超空泡长度Lc无量纲化处理。

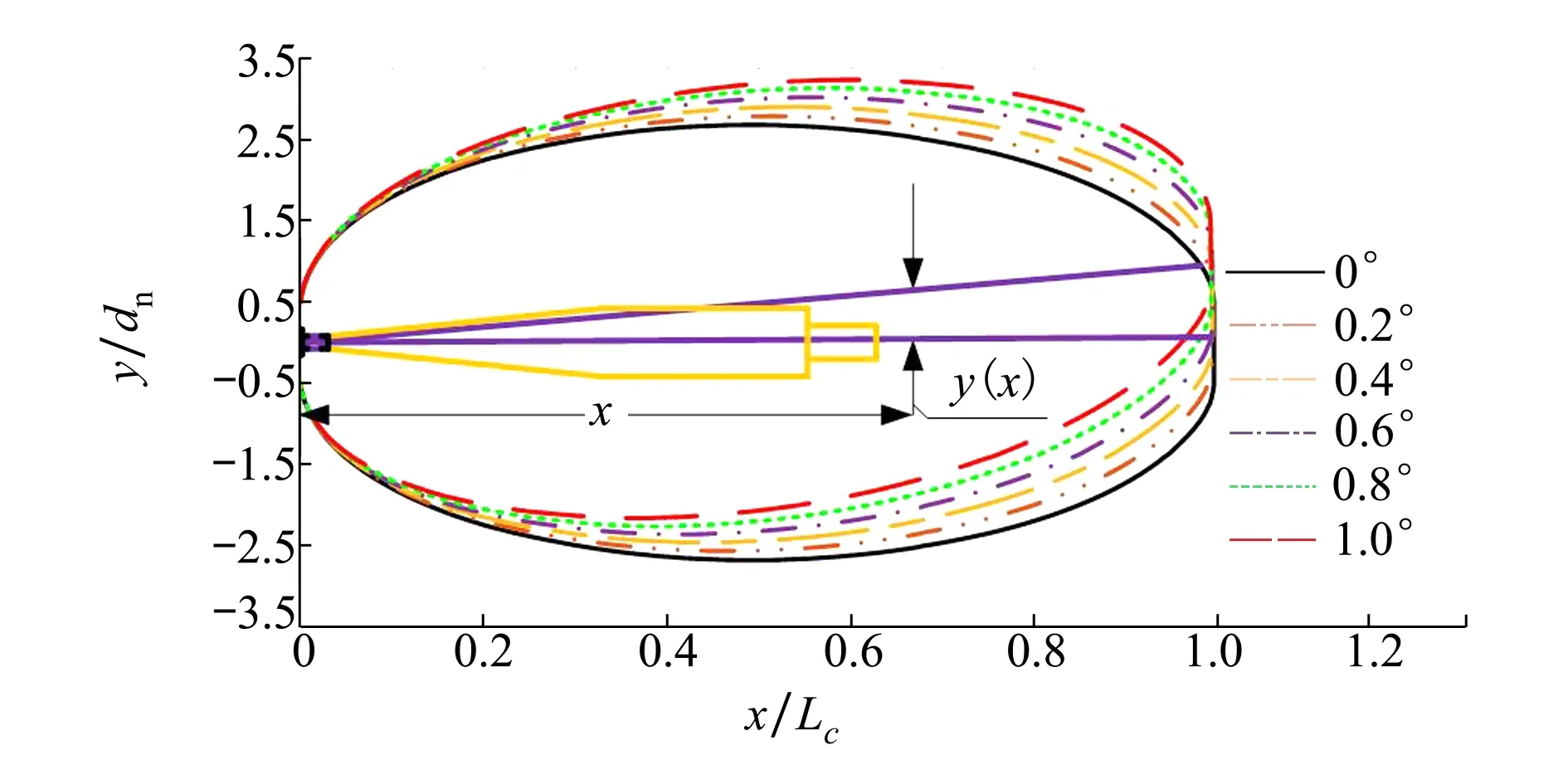
图5 不同攻角下超空泡对称面轮廓曲线

由图5可知,攻角存在时,通气超空泡形态发生显著变形,超空泡整体逐渐向上偏移。随着超空泡向后发展,偏移逐渐增大,此外,超空泡整体轮廓线也随攻角增加偏移逐渐增大。为对攻角引起的通气超空泡轮廓线偏移量进行定量描述,获得攻角对超空泡形变的影响特性,在同一空泡截面处(横坐标相同),以0°攻角的超空泡轮廓线为基准,将超空泡偏移量Δy=yα-y0进行无量纲处理,定义超空泡轮廓线无量纲偏移百分比Δh,如(24)式所示。

(24)

式中:yα为攻角α时纵对称面超空泡轮廓线纵坐标,m;y0为无攻角时同一截面的纵对称面超空泡轮廓线纵坐标,m。

根据图5可知,攻角的存在导致超空泡沿其发展方向不同位置的偏移量不同。为比较系列攻角在整个超空泡中的不同截面处Δh分布情况,定义无量纲空泡截面位置η,如(25)式所示。

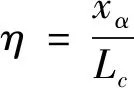
(25)

式中:xα为攻角α时某无量纲偏移百分比截面位置对应横坐标,m;Lc为攻角α时的超空泡长度,m。

以Δh=0.1,0.2,0.4为例,取相同无量纲偏移百分比Δh条件下系列攻角上、下轮廓线对应空泡截面位置η进行对比,如表1所示。

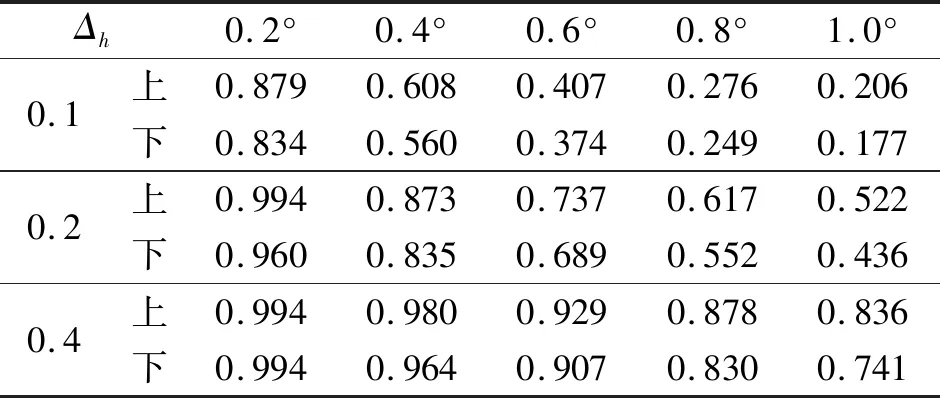
表1 上、下轮廓线相同Δh系列攻角不同η对比

由表1可知,上、下轮廓线在相同攻角条件下,η越大,Δh越大,说明越靠近超空泡后端,轴向变形越大;相同Δh条件下,随着攻角增加,η不断减小,这意味着Δh逐渐变大,空泡形变程度愈加严重。

此外,各工况条件下上轮廓η均大于或等于下轮廓,这说明系列攻角在相同Δh条件下,上、下轮廓线对应截面的偏移量是有差别的。值得注意的是,在系列攻角变化范围内,当上、下轮廓线Δh≥0.2时,η>0.436,这意味着系列攻角范围内,超空泡后56.4%部分轮廓线Δh>0.2,说明攻角对超空泡的偏移影响主要集中于空泡最大截面之后。

为比较超空泡相同截面处不同攻角上、下轮廓线偏移量变化情况,以攻角α=0.4°,0.8°,η=0.2～0.8处截面为例,以无攻角超空泡轮廓线为基准,研究相同截面处超空泡上、下轮廓线偏移量,如图6所示,超空泡纵轴使用dn做无量纲化处理。

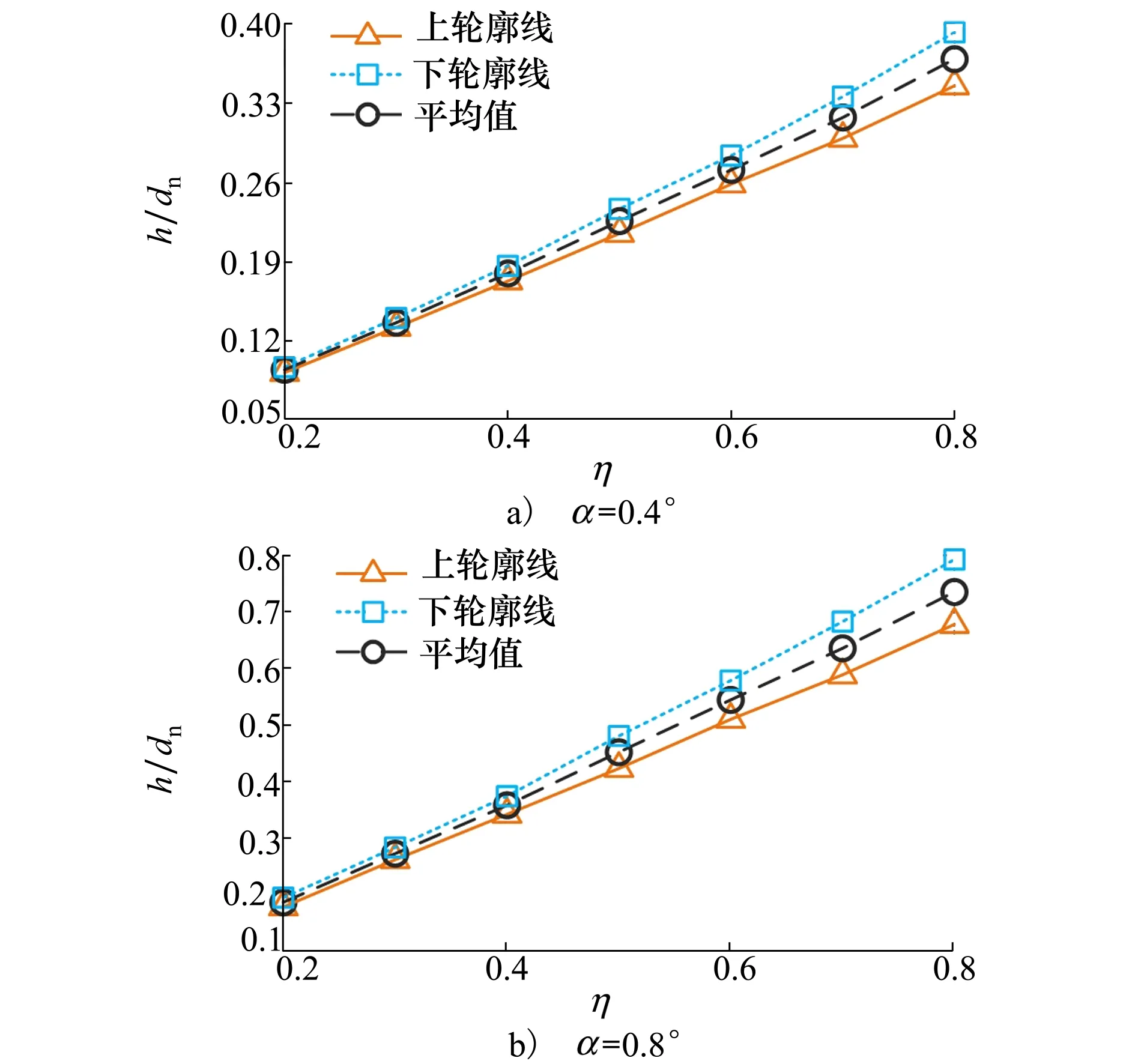
图6 相同截面上、下轮廓线偏移量对比

由图6可知,超空泡的上、下轮廓线偏移量随着空泡发展均为线性增长;相同η条件下,下轮廓线偏移量均大于上轮廓,且上、下轮廓线的偏移量差值在逐渐增大,但两者的平均值仍为线性。超空泡上、下轮廓线偏移量不同,说明超空泡不同位置处的发展情况不同,这可能与泡内气体流动结构有关,将在3.2.2小节中对流动结构充分研究,以便于分析超空泡不同形变特性的原因。

文献[3]指出若空化器相对来流存在攻角,空化器会受到升力作用并影响来流,进而导致超空泡向升力相反方向偏移。为更好体现出空泡偏移量,图7给出了系列攻角条件下超空泡轮廓中心线对比。其中包括以η=0.5,0.7,0.9为例,系列攻角下理论公式[4]计算的偏移量,x轴和y轴均使用Lc进行无量纲化处理。

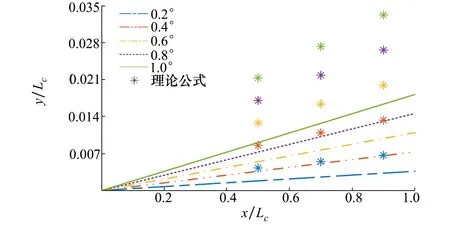
图7 不同攻角下超空泡轮廓中心线对比

由图7可知,随着攻角增大,中心线的轴向偏移量也越大,但仍为线性,且超空泡中心线的斜率随着攻角增加而不断增大。理论公式计算结果与数值计算结果规律一致,但随着攻角的增大两者之间的误差逐渐增大,在η=0.9处,α=1.0°时,理论计算结果是数值计算结果的2倍,误差非常大,意味着理论公式不适用于高弗劳德数条件下通气超空泡轴向偏移量的估计。这是由于理论公式推导过程中使用很多近似,且空泡尾部并没有采用高弗劳德数条件下的回射流闭合,此外,通气超空泡内包含气体流动,理论公式推导时,并没有考虑此情况。根据不同攻角对应的中心线斜率,建立攻角与超空泡中心线斜率的数学关系可得(26)式。

k=0.018 25·α

(26)

式中:k为超空泡中心线斜率;α为攻角。

攻角与超空泡中心线斜率呈线性关系。基于此,带圆盘空化器的航行器在高弗劳德数条件下超空泡中心线公式可定义为

y=k·x

(27)

式中:y为超空泡中心线偏移量,m;x为超空泡轴向坐标,m。

3.2.2 高弗劳德数下超空泡气体流动结构研究

通气超空泡流型变化可能与泡内气体流动特性有关,为了探究攻角对通气超空泡形变的影响机制,给出通气超空泡对称面上的速度变化矢量，如图8a)所示,气体流动结构示意如图8b)所示。图8a)中,黑色曲线为气相体积分数0.5的等值线,表示超空泡轮廓。由于航行器的存在,会对空泡内气体流动产生干扰,空泡不同位置的气体流动结构会有差异。为了展示空泡不同位置处的速度变化,对不同位置进行局部放大处理,其中A表示空化器后端;B表示锥段;C表示柱段;D表示尾段;E表示无体空泡壁面附近;F表示回射流附近。

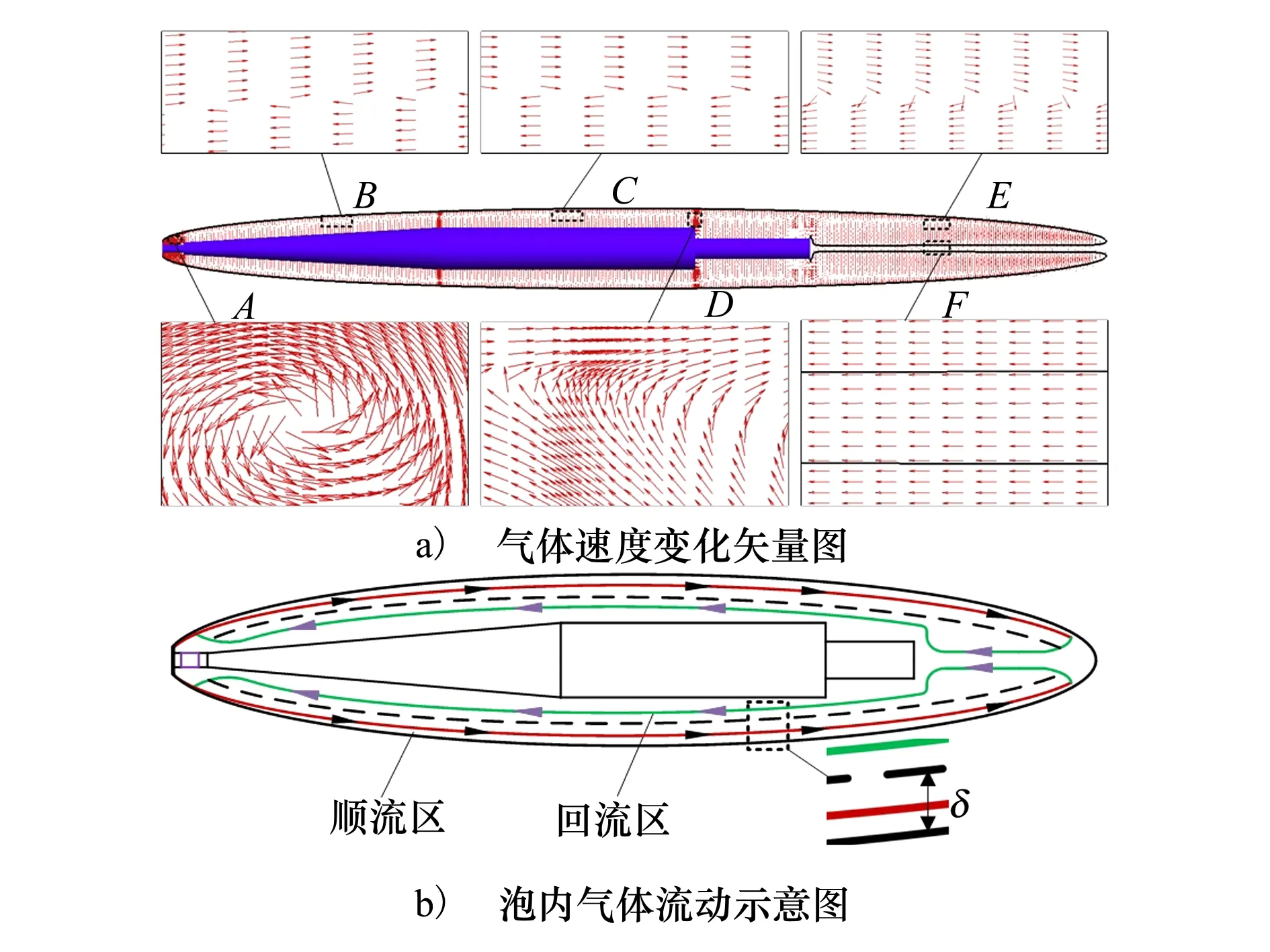
图8 超空泡气体流动结构

气体从通气装置喷出后,小部分气体在A处低压区形成小气体漩涡,另一部分沿着空泡壁面向下游流动(B,C,D,E处),到达空泡闭合区后,在高逆压梯度影响下,气体携带一定量的水反向流动进入泡内(如图8a)中F黑实线所示),反向流动的气体受到航行器尾部阻滞,气体分为了2股(D处),一股朝着负方向继续回流,另一股沿正方向随顺流气体向下游流动。

超空泡内气体流动示意如图8b)所示,其中,黑实线表示超空泡轮廓线,黑虚线表示顺流(红线)和回流(绿线)之间的分层线。由图8b)可知,超空泡内部气体存在大尺度漩涡,由顺流和回流2个流动方向相反的气体流动构成;空泡同一截面处,从上到下气体流动结构依次为“顺流-回流-顺流”。超空泡最大截面之前,通入气体后,空化器开始生成空泡,空泡径向尺寸向外扩张,将此区域定义为空泡截面膨胀区;空泡发展到达最大截面之后,空泡径向尺寸开始逐渐收缩,定义此区域为空泡截面收缩区。两区域空泡发展趋势不同,相应位置的气体流动结构也有差别。

以超空泡壁面附近两顺流区为例,研究攻角对超空泡内气体流动的影响。定义壁面附近顺流区径向宽度δ(如图8b)所示)表示超空泡轮廓到顺/回流分层线的径向距离。以超空泡最大截面前后7dn处为例,对比系列攻角空泡截面膨胀区和空泡截面收缩区δ大小,如图9所示,纵轴使用dn无量纲化处理。

图9 各攻角空泡上下表面附近顺流区域径向宽度

由图9可知,膨胀区和收缩区的顺流区域径向宽度δ随着攻角的增加均逐渐缩小。攻角从0°增加到0.4°时,膨胀区上表面δ缩小了0.038dn,下表面δ缩小了0.078dn,与上表面相比,下表面多缩小51.28%;收缩区上表面δ缩小了0.030dn,下表面δ缩小了0.23dn,与上表面相比,下表面多缩小86.96%。攻角增加到0.8°时,膨胀区上表面δ再次缩小0.033dn,下表面δ再次缩小0.053dn,收缩区上表面δ再次缩小0.06dn,下表面δ缩小了0.11dn,下表面δ缩小幅度更大。此外,结合图9可知,膨胀区上、下表面δ的差值比收缩区更小。

随着攻角的增加,来流在体坐标系中的径向速度分量增加,直接作用于超空泡下表面,下表面顺流区受挤压严重,δ明显缩小,下表面膨胀区发展减缓,收缩区发展加剧;上表面离来流作用位置较远,攻角作用经回流区传递到上表面时扰动已经减弱,因此上表面附近δ变化平缓,与上表面相比,下表面附近δ变化量更大,故下表面偏移量也更大;截面膨胀区的上、下表面δ的差值比收缩区小,意味着来流径向速度对收缩区的下表面影响更大。空泡壁面附近δ的变化说明超空泡下表面受来流影响后,泡内气体流动方向发生改变,并沿空泡截面传递作用于整个超空泡,导致其整体有轴向偏移的趋势。

空泡截面膨胀区和收缩区上、下表面附近δ发展趋势不同,相应位置的气体流动结构也有差别。为定量研究2个区域内的气体流动情况,分别对比系列攻角下,7dn截面处膨胀区和收缩区的上、下表面的气体径向速度vy如图10所示,y轴正方向为速度正方向。

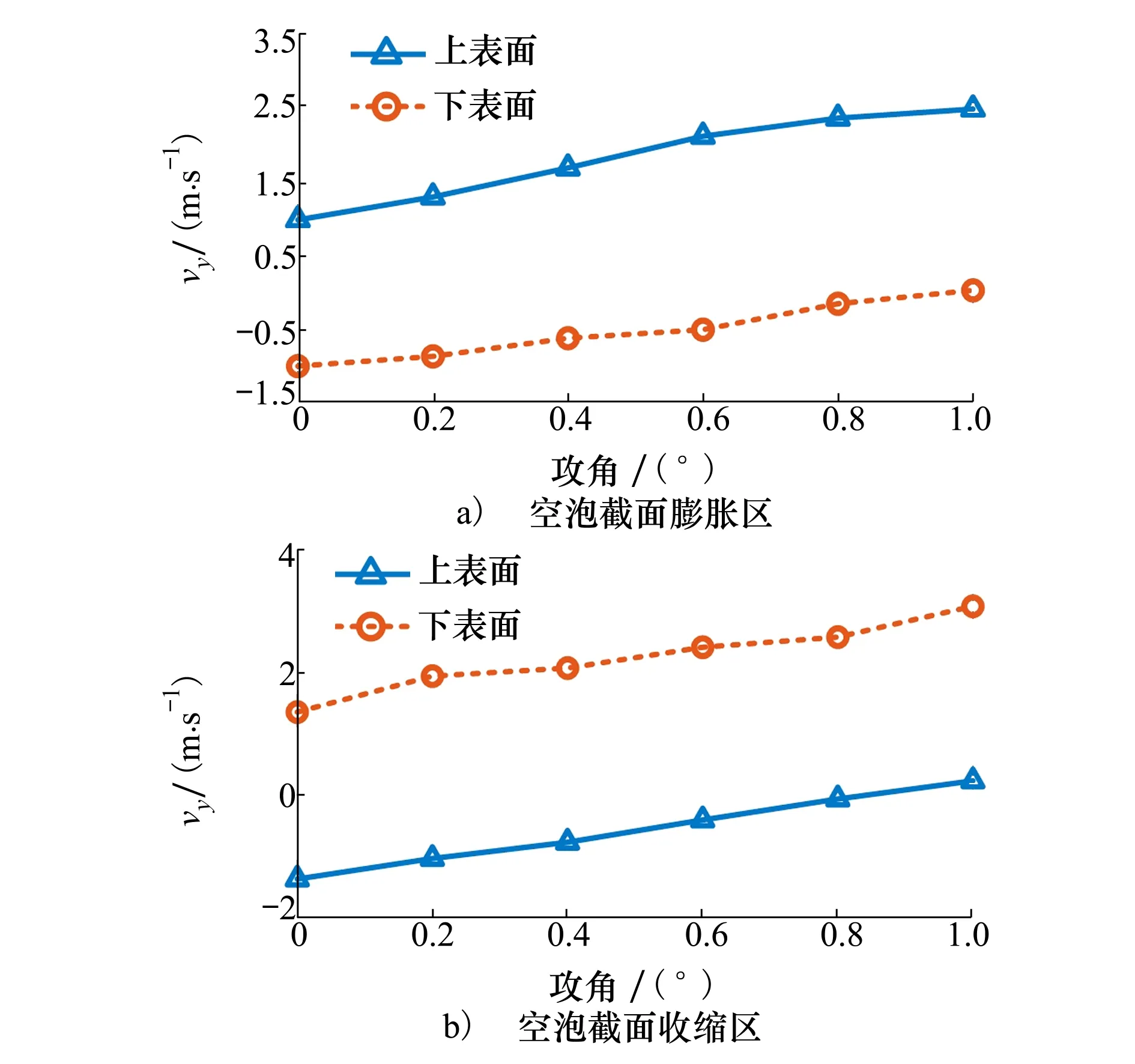
图10 空泡上、下表面气体径向速度

图10a)中,空泡截面处于扩张阶段,上表面气体速度为正,下表面为负,随着攻角的不断增加,上、下表面气体径向速度变化率为正。攻角从0°到1.0°,上表面径向速度增大了1.49 m/s,下表面径向速度虽然为负,但速度绝对值减小了1.02 m/s,膨胀区上表面附近气体向上运动趋势加剧,下表面附近气体向下运动的趋势减缓。

图10b)中,空泡截面处于收缩阶段,空泡的上表面气体径向速度为负,下表面为正。随着攻角增加,上、下表面气体径向速度变化率为正。攻角从0°到1.0°,上表面气体径向速度变化量为1.63 m/s,且径向速度方向由负变正,下表面增加了1.76 m/s,收缩区上表面气体的向下发展趋势减缓,下表面气体向上发展趋势加剧。

攻角增大,两区域上、下表面整体速度变化率为正,气体流动整体向上发展。膨胀区上表面气体向上发展趋势加剧,下表面气体向下发展受抑制,结合图8可知,来流径向速度对截面膨胀区影响较小,故其速度变化也不大,相应偏移量也较小,这与3.2.1节中结论相符;收缩区上表面气体向下发展受抑制,下表面气体向上发展加剧,且来流径向速度对收缩区影响较大,速度变化较大,越靠近超空泡后端,偏移形变越大。