数学严谨性分析

丁传松

(西北师范大学 数学与统计学院，甘肃 兰州 730070)

1 严谨性是数学的基本特点

数学严谨性体现在数学的各个分支与各个部分之中，但最早、最有影响的当属于2300多年前欧几里德的《几何原本》.《几何原本》是人类文明史上最具有历史意义的杰作之一，它用公理化方法把一些最基本的几何元素，根据几条“不证自明”的公理公设按逻辑演绎方法，将此前所积累的大批零碎、片断的几何结论和有关数学知识搭建起严谨体系，构建成一座宏伟稳固的数学大厦.虽然不能说天衣无缝，也真的叫人叹为观止！以致在当时或后来的2000多年都被膜拜为最严谨的体系.人们通过学习欧几里德《几何原本》的公理化理论，得到思维训练与提升，不仅推动数学各分支公理化体系的进展，也对自然科学甚至对社会科学产生启示，已经为公众所认知与肯定.

伟大的科学家牛顿高度赞赏《几何原本》“从这么少的几条外来的原理，就能够取得那么多的成果，这是几何学的光荣[1].”在《几何原本》的启发下，1687年，牛顿完成了划时代的经典巨著《自然哲学的数学原理》，这部巨著就是以他提出的“万有引力”为基础，用他创建的微积分和其他数学方法严谨地逻辑演绎出所有物理现象(从日常苹果落地到宏伟的天体星球运行规律)，可见《几何原本》严谨性的影响之大！微积分的另一伟大创建者、数学家莱布尼茨是在法律领域自觉运用数学理性的第一人.在《法律教习新方法》一书中,莱布尼茨论证道:法律应被视为一门依据几何模型对第一原理进行演绎的科学,法律推论必须遵循几何证明中的推证模型[2].

几何公理化思想推动了自然学科和社会学科的发展，各学科开始注重本学科的数量分析和逻辑推理，仿照数学方法用最基本原理来解释本学科众多的现象.正如史密斯所说“假如说几何不严密，那么就什么也不是了……，在严密这一点上，普遍都认为，欧几里德的方法是无懈可击的[3].”

2 数学的严谨性不是绝对的

数学的严谨性虽然值得称颂，但它不是绝对的，而是有时代背景的，今天看来是严密的，或许明天就发现有漏洞；今天发现的不严密之处，明天可能就被弥补纠正过来了.我们通过数学中3个事例来说明数学对不严谨问题的漫长认知过程.

2.1 《几何原本》并非无懈可击

被举世推崇的欧几里德的《几何原本》并非无懈可击的，后人逐渐发现其中有一些不太严密的情形，需要加以修正，例如，《几何原本》讨论的几何图形不因移动而改变，图形全等可借助于图形的搬动重合来实现，现代人却认为不明确地界定“刚性”应该是不严谨的！同样，欧几里德时代人们理解的线段是连续、不间断的，自然平面上两条不平行的直线必有交点，这是一目了然的事情，后人则要求有连续性公理保证.如此种种，修改后才得以完美.

2.2 对数的认识不全面

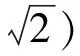
2.3 对微积分的理解不完整

微积分是人类智慧的结晶，是17世纪最伟大的数学发明，牛顿和莱布尼茨同时成为微积分的开创人.微积分的创建是继欧几里德《几何原本》之后数学最伟大的成果，它解决了17世纪之前积累下来的最重要科学问题，如：运动中速度、加速度之间的相互关系，曲线与切线、法线、曲率的关系，发射角与射程和高度的极值关系，弧长、面积、体积的计算.这些问题在过去1000多年间，只对特殊问题有极特殊巧妙之解法，却没有彻底的一般理论与具体方法，由此可见微积分的伟大意义.可是如此有意义的微积分却存在严谨性问题，拙作“这一句话的修改用了三百年[4]”一文曾提到：直到牛顿时代，人们对极限思想的理解还是不完整的，对极限定义的描述也不够准确.

牛顿在《自然哲学的数学原理》第一编“物体的运动”第一章“初量与终量的比值方法”中开宗明义：“量以及量的比值，在任何有限时间范围内连续地向着相等接近，而且在时间终了前相互趋近，其差小于任意给定值，则最终值必然相等.”牛顿完全意识到他的这一表述很难被读者接受，因为很难理解“最终值”、“相等接近”的含义，因此，牛顿在他的巨著附注中用了很大篇幅，不厌其烦地耐心解释和说明，如巨著附言中说“可能会有人反对，认为不存在将趋于零的量的最后比值，因为量在消失之前，比率总不是最后的，而当它消失时，比率也就没有了.”“根据同样的理由，我们也可以说物体到达某一处所并在那里停止，也没有最后速度，在它到达之前，速度不是最后速度，而在到达时，速度没有了.回答很简单，最后速度意味着物体以该速度运动着，既不是它到达其最后处所终止运动之前，也不是其后，而是在它到达的一瞬时，也就是说物体到达其最后处所并终止运动时的速度.”特别地，牛顿担心他著作的全部也有同样问题，所以特别声明:“如果在下文中，出于易于理解的理由，论及的最小的，将消失的，或最后的量，读者不要以为是在指确定大小的量,而是指作无止境减小的量.”通过如此多的篇幅来做补白与说明，句句正确且深刻，可以看出他千辛万苦说明的：最小的、最后的、即将消失的、最后所终止的，其实就是今日所理解的“无穷小量”和“变量收敛的极限”！

因为微积分需要用无限的过程来解决瞬时速度(一系列平均速度的趋势)或面积(一系列矩形面积的逼近)的问题，这种无穷过程与有限过程有最本质区别，它没有最后，只有持续稍后，它没有最小(大)只有更小(大)！可见只有深刻领会无穷，才能把握无穷小量，严谨处理微积分的问题.

3 数学严谨性最大的挑战者是“无穷”

数学的严谨性最大的挑战者是“无穷”，当对“无穷”有了深刻认识后，数学的严谨性获得了极大提高.

自从康托用“一一对应”思想引进了两个集合的元素个数(势)相等定义之后，人们对无限集的理解大大深化了，首先就对“整体大于部分”这个曾为颠不可破的真理发生了动摇，这是亚里斯多得和阿基米德曾将它用作为公理来认可的事实.但是对无限集就不适用了！无限集的本质居然就是：能与其一些真子集建立一一对应关系，通俗地说，就是：无限集与其中一些真子集的元素个数一样多，而有限集则根本不可能！

有了“无限”的概念，需要刷新的观念就太多了！我们在最熟识的实数系和实变函数中，过去从来没有想过的事情出现了：有理数居然与自然数一样多，直线上与平面上的点一样多，存在测度(广义的长度)为0的处处稠密集，也存在测度大于0的疏朗(无处稠密)集.我们曾经直觉地(不严谨地)认为连续曲线应在每点处有切线，顶多除了个别点(折点)例外，当魏尔斯特拉斯构造出一个处处连续无处可导的函数(直观想像是一条处处连续曲线却处处是折点无切线)，人们才大开眼界!更奇怪的是：原先以为这种函数最初是由个别数学家精心炮制、矫揉造作出来的个别特例，谁知却能证明实变函数中绝大部分是这些函数！这表明我们在微积分中所研究的满足微分方程的函数真是少之又少呀！

也许有人要问：这些千奇百怪的事实与观念是真的吗？有用吗？当然是真的，也极其有用.例如，由于区间上对某些稠密集可用无限个长度之和可以任意小的区间所覆盖，这样它的测度为0(而仅用有限个具有上述性质的区间是办不到的)，这些集合称为Lebesgue零集，处理好这一零集，Riemann积分可进一步提升为Lebesgue积分，甚至Henstock 积分，预示微积分得到了进一步发展，理论也更完整了，意义极大！

数学系三年级有学生提问：我们从初中开始学实数和函数，这么多年已经扩展到复数、向量、数组、映射、复变函数和泛函算子了，现在怎么回头还来学实变函数论呢？并且还这么难？其实，这门课程真正要学习的是“无限”，并且将“无限”用于最简单的实数集、实变函数研究，这样过去的观念需要更新，但这仅仅是起步，今后要深入到更多领域，任重道远.这对其他概念的再理解再学习，意义可大！

4 适当突破严谨性也是一种思路创新

严谨性虽然很重要，但有时跨越严谨性也很重要且有其意义.严谨性是数学的特点，数学家们为之奋斗追求，但他们并没有把严谨性作为一种约束.《几何原本》的不严谨并没有削弱它的辉煌成就，微积分的不严谨也并不妨害其广泛应用，数学大师们没有将这些不严谨作为科研前进道路上的绊脚石.相反，在不严谨的想象中充分捕获灵感，会产生新的突破.这里用级数发展过程来加以说明.

回想一下，初中代数一开始就是用符号代表数，虽然初中生并没有弄清实数的概念，但却要求对实数的运算严格规范，几条公理公法必须遵守，如等量公理、结合律、交换律和分配律等.这些公理公法只对有限运算有效！初中只讨论有限，自然不需要特别注明.但等到学习无穷级数时，如果对无穷级数不分青红皂白，依然按老规律运算，就会产生悖论.

例1滥用结合律3种演算3种结果.

(i)s=1-1+1-1+1-…=

(1-1)+(1-1)+…=0;

(ii)s=1-(1-1)-…-(1-1)-…=1;

(iii)因为

s=1-(1-1+1-…+1-1+…)=1-s,

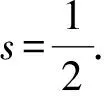
例2难以接受的结论.

因为

所以

(i)令x=-1，则

(ii)令x=2，则

s(2)=1+2+4+8+…+2n+…=-1;

(iii)令x=3，则

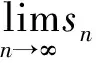
可是这对不收敛级数不公平！为什么不在这一系列数据中提炼出来一些有用的结果呢?浪费资源太可惜了，数学家们心里自然很牵挂，Cauchy定义了收敛级数，他还在研究发散级数，写了题为《论发散级数的合理运用》的文章.皮尔庞特说：“在这个世纪已认为要断然从严密数学中驱逐出去的那些级数，在这个世纪末竟又重敲接纳之门，这确实是我们科学的一个奇怪的变迁[3].”

下面用一种公理化方法来探讨这个问题.用公理化方法突出极限的几条本质属性，刻画级数求和的定义.

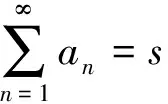
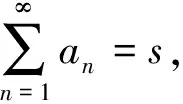
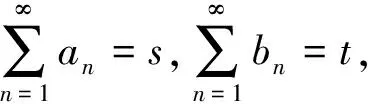
(C)若a1+a2+a3+…+an+…=s,则

a2+a3+…+an+…=s-a1，

反之亦真;

(D)若a1+a2+a3+…+an+…=s，则

(E)若对任何的自然数n，部分和Tn=a1+a2+…+an≥0，则s≥0.

命题1级数“*收敛”与Cauchy意义下的收敛是等价的.

证明Cauchy意义收敛级数自然满足“*收敛”的各条性质，反之若级数“*收敛”，则必有：对任给ε>0,|Tn-s|<ε除了顶多有限项以外对所有n均成立.因为不然，必有ε0>0及无限多个nk，使得|Tnk-s|≥s0.不妨设Tnk>s+ε0，则

这与“*收敛”的性质(D)矛盾，即得Cauchy意义收敛. 】

“*收敛”没有任何“趋势”或“归宿”直觉的感觉！我们证明了“*收敛”、“*和”与Cauchy意义下的级数收敛与级数和是完全等价的.

所谓扩充级数求“和”或者说发散级数求“和”，换一种说法就是要引进一种加法运算“”，使得对有限个实数求和时，按“”相加的结果与通常加法“+”相加的结果是一致的，而对无限个实数求和时，按通常加法运算“+”相加时在Cauchy意义下是收敛的，则按加法运算“”相加的结果是一致的，但反之不然！即按“”相加有结果，级数a1+a2+a3+…+an+…未必在Cauchy意义下收敛！更谈不上相加的“和”相等.这是级数求和的扩充，或者说引进了一个发散级数的“和”.

公理1引进新的加法运算“”，它的有限实数的加法与通常加法“+”一致，并且对于数列{an}，记H(an)=a1a2…an…，若存在实数s，满足下列性质：

(A)若H(an)=s,H(bn)=t,则H(an+bn)=s+t，即

(B)若H(an)=s,即a1a2…an…=s,则a2a3…an…=s-a1.

(C)若H(an)=s，则(a1a2…an1)(an1+1an1+2…an2)…(ani+1ani+2…ani+1)…=s;

(D)若对任何自然数n，部分和Tn=a1a2…an≥0，则s≥0.

则称该级数和为s.

这是级数Cauchy意义下收敛的公理化定义，如果增加级数性质，如与排列顺序无关可得出绝对收敛级数.放宽约束会有更多发散级数有“和”，Hardy规定了级数运算自明公理[5]，只用了性质(A),(B)和(C).

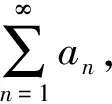
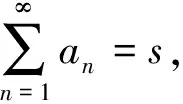
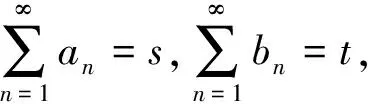
(C)若a1+a2+a3+…+an+…=s，则

a2+a3+…+an+…=s-a1，

反之亦真.

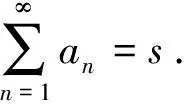
从公理2出发，可知例1的第三种方法是可取的，而第一、二种方法不行.例2的演算是正确的.更有趣的是：

设s=1-2+3-4+…,则应用性质(A),(B)和(C)可得

所以

这样轻易获得一些发散级数的“和”，貌似离奇，但是唯一确定的，想必有其可取之处，将其中意义揭示出来，才更有意思！量子理论已经隐含了它的意义.真是：山穷水尽疑无路，柳暗花明又一村！