非均匀等离子体中的相对论球形等离子体波

成丽红,张小波,唐荣安,张爱霞,薛具奎*

(1.贵州工程应用技术学院 理学院,贵州 毕节 551700；2.西北师范大学 物理与电子工程学院,甘肃 兰州 730070)

随着激光技术的发展,对等离子体波的理解和等离子体波在实验中的应用都取得了巨大的进展.在等离子体中,强激光的非线性效应激发的等离子波,也称为尾场波,可以提供非常强的纵向电场,从而加速带电粒子[1-3],而且实验上成功实现了高品质、超短电子束的产生[4-5].只有了解了如何在等离子体波的加速场中注入电子,激光等离子体的加速机制才得以真正揭示.加速过程中,成功注入同步的电子束,即电子的初始运动状态保持一致,是产生准单能、低散射高品质电子束的关键[2].无论是在激光尾场加速机制中,还是在激光直接加速机制中,恰当的电子注入都至关重要.在激光等离子体加速电子的相关实验中,即使没有外部电子注入,也会发现有电子被加速,这是因为利用等离子体波破裂也可以实现激光等离子体加速的电子自注入[6].对于小振幅的电子等离子体波,波形为正弦形式,随着振幅的增大,等离子体波形发生变化,像锯齿形,如果振幅继续增大,超过等离子体波可以承载的最大振幅,就会出现波破裂.纵向波破裂和横向波破裂都可以导致电子注入.

许多研究工作说明在非球形等离子体波中,波破裂是可控的[4,7-10].在非均匀等离子体中,等离子体波的相速度和电子振荡的频率都会随位置变化,导致邻近的电子振荡方向相反,出现波破裂.沿着激光传播方向上,无论是密度增加还是减小,都有利于激光的局域化和电子自注入[4].在以往的球形等离子体波[11-12]研究中发现,相对论球形等离子体波具有连续谱的特征,导致出现相混合和波破裂,可用于电子加速过程中电子自注入[12].

文中将研究密度非均匀对球形等离子体波及波破裂的影响.文中第1部分给出物理模型,即研究球形等离子体波的基本方程组；第2部分将利用欧拉法转化为拉格朗日法,得出非均匀等离子体中的波破裂条件以及电子(可以看作为等离子体的流体元)的振荡轨迹；第3部分研究了等离子体波破裂,并估算了等离子体波破裂的时间.

1 物理模型

采用电子-离子的双组分等离子体,初始时刻电子和离子的密度沿径向呈现非均匀分布,但是离子近似看作不动(mi≫me),仅仅提供固定的背景场.电子近似看作流体,通常研究等离子体采用欧拉法,也就是用场的观点来研究电子流体的运动.所以模型采用的方程有麦克斯韦方程组和电子的流体方程组.等离子体的参量和场的变化量都是径向坐标r和时间t的函数.采用的方程组为无量纲的形式

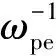
Ni0(r)-ne0(r)=0.

(5)

2 球形等离子体波

为了方便研究球形等离子体波,电子的运动将用拉格朗日坐标表示(r0,t),把欧拉坐标(r,t)转化为拉格朗日坐标(r0,t),具体的关系式为

r=r0+ξ(r0,t).

(6)

其中，r0为电子的初始位置；ξ(r0,t)为电子相对初始位置发生的位置偏移.根据(6)式,求解密度连续性方程(1),得到电子的密度分布表达式

ne(r0,t)=ne0(r)[J(r0,t)]-1.

(7)

ne0(r)=n0(1+br).

(8)

其中，b为密度非均匀参数,b>0表示等离子体密度从球心处沿着径向线性增加,b<0表示等离子体密度从球心处沿着径向线性减小.

研究电子的运动,除了需要确定电子的密度分布,还需要确定电子的位移偏移量ξ=ξ(r0,t)的变化率.利用(6)式,方程(2),(3)和(4)在拉格朗日坐标下的形式表示为

求解泊松方程(10),得到等离子体波的电场E为

(11)

根据(11)式,可以看出,电场强度E与电子的初始坐标r0和非均匀参数b有关.

联立求解方程(8),(9)和(11),就可以得到电子的运动积分方程,确定电子的位移偏移量ξ=ξ(r0,t)与初始参量之间的关系

(12)

(13)

根据(13)式便可得到电子的动量和位移的相平面(p,r)内的电子振荡轨迹图,如图1所示.为了对比,图中所有的实线表示密度均匀的等离子体中电子的轨迹图,电子在初始位置附近做周期性振荡.其中,图1a中的虚线表示当电子的初始位置r0和初始动量p0确定(r0=2,h=5)时,且电子的初始密度沿径向线性增加时,电子做周期性振荡,但是振荡振幅减小.根据图1a不同的虚线,随着b的增加,即非均匀强度的增加,电子的振荡振幅变小, 但是永远无法到达中心(r0=2)处, 这是因为(7)式表示的电子密度演化公式在ξ=-r0存在奇点.图1b与图1a相比,增大初始动量p0(h=15),其他参数均不变的情况下,电子振荡的振幅增加.图1b中的虚线表示和图1a中相同的结论,非均匀强度的增加,电子的振荡振幅变小.

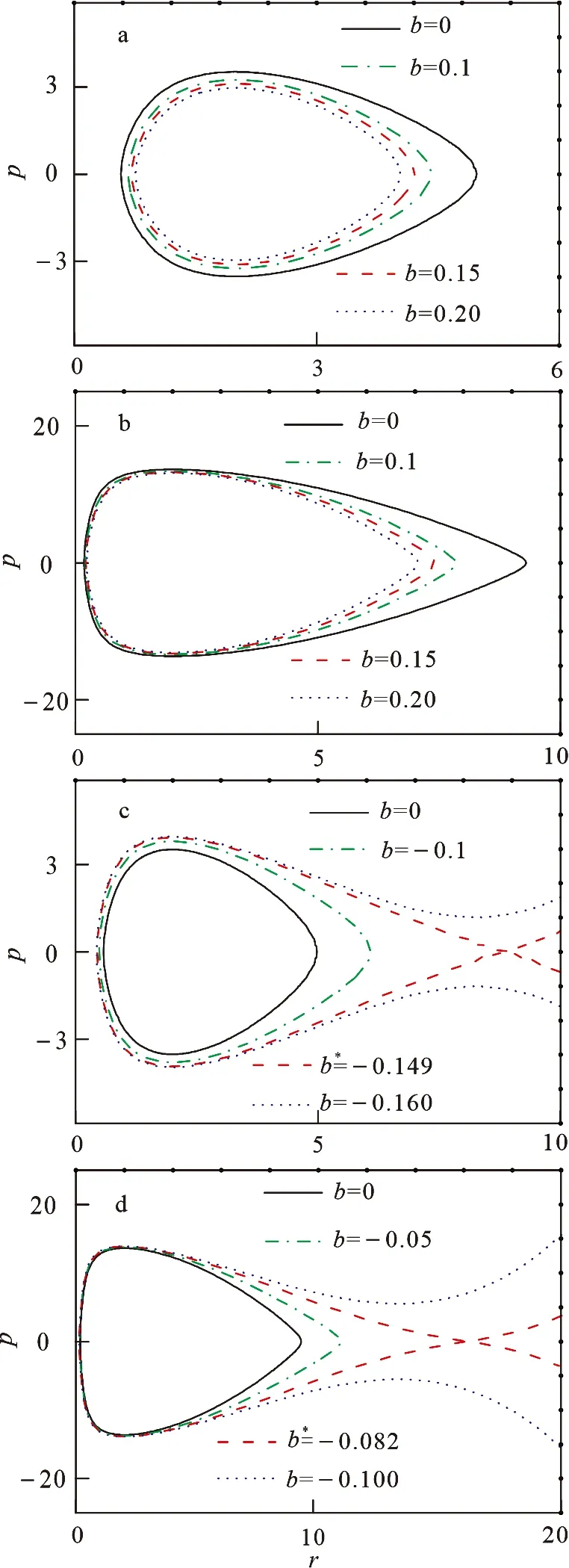
a.r0=2,h=5,b>0; b r0=2,h=15,b>0; c.r0=2,h=5,b<0; d.r0=2,h=15,b<0.

当电子的初始密度沿径向线性减小时b<0,电子振荡轨迹如图1c和图1d所示,其它参数均与图1a和图1c相同.对比图1c和图1d中不同的曲线,随着非均匀参数绝对值的增大,等离子体密度的变化率增大,电子振荡的振幅增加.如图1c和图1d中短虚线显示当非均匀参数接近一定值时b=b*,电子将无法做周期振荡.

总结图1的现象,均匀等离子体中电子会在其初始位置附近做周期运动,会自发的产生电子振荡；等离子体密度沿着径向增加时,电子振荡的振幅减小；等离子体密度沿着径向减小时,电子的振荡振幅逐渐增加.特别是当等离子体密度沿着径向减小,密度的变化率达到并超过一定的临界值时,电子的周期性振荡将变为非周期振荡.图2给出了电子的初始密度沿径向线性减小时非均匀参数b的临界值b*.如图中蓝色实线所示,r0=2时,非均匀系数和电子初始动量的参数空间(b*,h)被分为两部分,左下部分表示电子做周期运动,即等离子体中存在电子振荡,右上部分表示电子将做非周期运动.只要给定适当的参数,就可以确定电子能否做周期运动.

图2 r0=2时,非均匀参数和电子初始运动的参数空间(b*,h),电子分别呈现周期性振荡和非周期振荡

当电子可以做周期振荡时,通过求解(9)式可以确定振荡频率和周期.在非线性极限近似条件下ξ

(14)

其中，右端的3项为非线性项,都与非均匀参数b有关.右端第1项和第2项可以归为一类,源于振荡的球对称结构,第3项是由相对论效应引起的.利用摄动法求解(14)式,展开位移ξ=ξ0+ξ1+…和振荡频率ω=ω0+ω1+….求得零阶的解为：

ξ0=κ(r0)cos(ω0t).

(15)

其中,κ(r0)为电子振荡振幅.假设振幅κ(r0)不随初始位置变化,取值κ(r0)≈1,振荡频率与初始位置r0、非均匀系数b关系表示为

(16)

且关系如图3所示.左右图中黑色实线说明在均匀等离子体中,周期T=2π/ω随着初始位置r0的增加而增加,频率ω随着初始位置r0的增加而减小.

图3a中,不同的线表示等离子体密度沿径向增加,随着非均匀系数的增加振荡周期变小,这与图1a和图1b的结论一致,振幅减小,周期自然减小.总之，沿着径向增加的等离子体密度会抑制电子的振荡.

图3 不同非均匀参数b下,振荡周T与电子初始位置r0的关系

图3b中,不同的线表示等离子体密度沿径向减小,随着非均匀强度的额增加振荡周期变大.当b=-0.08时,密度沿着径向急剧减小,远离球心的电子的振荡周期急剧增加.综合图1c和图1d与图3b的结论,沿着径向减小的等离子体密度会增强电子的振荡,而且对远离球心位置的电子影响变大.

3 球形等离子体波破裂

根据第2部分中(16)式的结论,振荡频率与初始位置r0、非均匀参数b均有关.当非均匀参数b确定时,振荡频率随初始位置r0连续变化,表明电子振荡具有连续谱,会出现相混合,进而发生波破裂[12].为了估算波破裂的时间,将电子的位移偏移量ξ(r0,t)在r0处进行傅里叶展开得到

(17)

其中ω(r0,b)由(16)式给出.ξ(r0,t)分别对r0和t求导可得

并且在t→∞的近似条件下,(18)式右端的第1项明显小于第2项,联立(18)式和(19)式得到如下的关系

(20)

将(7)式得到的波破裂条件∂ξ/∂r0=-1代入(20)式得到波破裂时间的估算方法

(21)

在强相对论等离子体中,电子振荡速度接近光速c,即ve=∂ξ/∂t≈1,同时将(16)式代入(21)式,得到波破裂时间和初始位置、非均匀参数的变化关系,具体如图4和图5所示.

图4 等离子体初始密度沿径向线性增加时,波破裂时间tbr与r0和b的关系

图5 等离子体初始密度沿径向线性减小时,波破裂时间tbr与r0和b的关系.

图4a给出了等离子体密度沿着径向线性增加时,波破裂时间tbr随初始位置r0和非均匀参数b的变化图.均匀等离子体中(等高图的左侧边界),波破裂tbr的时间随着初始位置r0的增加而增加,说明在靠近球心处容易发生波破裂.图4b说明,位置确定时,随着密度的增加,发生波破裂的时间明显变长.对比不同位置对应的3条线可以发现，随着密度的增加,远离球心的位置发生波破裂的时间明显变长.密度的非均匀性对外层电子的影响更大.结合第2部分的结论,等离子体密度增加时,电子振荡的振幅减小,周期变短,电子的运动状态不易发生改变,发生波破裂的时间变长.

图5a给出了等离子体密度沿着径向线性减小时,波破裂时间tbr随初始位置r0和非均匀参数b的变化.均匀等离子体中(等高图的左侧边界),波破裂tbr的时间随着初始位置r0的增加而增加,但是随着等离子体密度的进一步减小,不同初始位置发生破裂的时间趋于一致,如图5b所示.结合第2部分的结论,等离子体密度减小时,电子振荡的振幅增加,周期变长,导致电子的运动状态更容易发生改变,发生波破裂的时间变短.

4 结论

理论上研究了相对论球形等离子体的动力学特点,由于球形等离子体波具有连续波的典型特征,会产生相混合及波破裂现象.理论研究发现,通过调节等离子体的初始密度分布,可以改变等离子体中电子的振荡周期和振幅,进而调节波破裂时间.当等离子体的初始密度沿径向线性增加时且继续增加非均匀强度时,电子振荡振幅减小,周期变短,电子的运动状态不易发生改变,延长波破裂时间.反之,当等离子体的初始密度沿径向线性减小时,缩短了波破裂时间.总之,理论研究发现通过调节等离子体的初始密度,可以实现调控球形等离子体波的波破裂时间,为激光等离子体加速器中注入合适的电子提供了一种方法.