广义带有随机活化机制的钝化网络模型研究
2023-01-10王学文罗月娥冀慎统
王学文,罗月娥,冀慎统
(1.景德镇学院 信息工程学院,江西 景德镇 333400;2.景德镇学院 机械电子工程学院,江西 景德镇 333400;3.贵州师范学院 物理与电子科学学院,贵州 贵阳 550018)
复杂网络是研究复杂系统的有力工具.每一个复杂系统都可以从实际出发,抽象成由大量具有相互作用的个体所组成的复杂网络[1-3].例如在科学引文网络中,用网络中的节点来代表期刊上发表的科学论文,用节点之间的连边来代表从一篇论文到另一篇之前发表的论文的引用[4].真实世界中普遍存在老化现象,因此,老化机制对复杂网络的形成过程起重要的作用.例如在科学引文网络中就存在着一个半衰期效应,表现为老的文献很少被引用.为了研究老化效应对网络演化的影响,一些研究者考虑了时间老化因素的影响[5-19].Klemm等在对科学引文网络研究时,发现节点在加入网络后只有有限的时间获得连边,从而提出了基于度驱动的钝化网络模型(KE网络模型)[8-9].在该模型中,节点的钝化机制能够显著地增加网络中的三角形数目,提高网络的聚类系数.近年来,许多国内的学者也在KE网络模型的基础上做了许多有益的工作.例如在考虑了连边权重的基础上,吴枝喜等[11]提出了基于权重的钝化网络模型,在权重方面拓展了钝化模型.考虑到网络中当前可选目标的绝对重要性很难获得,而相对重要性更加容易获得的情况,许新建等提出了基于序排列的钝化网络模型[13].该网络模型采用了序偏好机制来刻画网络节点的老化情况,在该方面对钝化模型进行了扩展.考虑到实证引文网络中有部分文章是在后期才被人们关注的现象[19-21].本研究小组提出了带有活化机制的钝化网络模型,该网络模型通过引入活化机制使得文章后期被引用成为可能[14-15].
在以上所提到的钝化网络模型中,要求新进节点必须与当前的每个活跃态节点都连接,这样的限定不能反映真实引文网络中的随机效应[22].另外,考虑到真实引文网络中可能被引用的文章数目大于最终被引用的文章数目的情况,对应于钝化网络模型中的活跃态节点的数目大于新进节点的连边数,论文提出了一种广义的带有随机活化机制的钝化网络模型.在该模型中,不仅考虑了节点状态的转变,还考虑了新进节点可以从当前的活跃态节点中随机选取一定数量的节点建立连接的情况.文中对该模型的整体入度分布进行了理论解析和数值模拟.最后,将3个实证科学引文网络的实证数据与该模型的数值模拟结果进行了比较.
1 网络模型
受之前工作的启发,文中提出了一个广义的带有随机活化机制的钝化网络模型.在该模型中,网络中已有节点的可能状态有两种,活跃态和休眠态.新加入的节点一开始处于活跃态,随着网络的演化逐渐老化直到失去活性变成休眠态,然而处于休眠态的节点又存在一定的概率被选择进行活化,从而成为活跃态节点.具体的网络演化模型如下:
1)初始网络中存在M个活跃态节点,其余的均为休眠态节点.
2)从当前的M个活跃态节点中选取m(m≤M)个活跃态节点.

4)从当前的所有休眠态节点中随机选取一个休眠态节点进行活化,使其由休眠态变成活跃态.
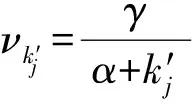
6)返回第2步,让网络进行循环演化直到网络尺寸达到设定的规模N为止.
根据该模型,只有活跃态节点能够获得新进节点的连接,并且在网络演化过程中活跃态节点可能成为休眠态节点,这个过程可以认为是一个“遗忘”的过程.与此同时,休眠态节点能够再次被选择成为活跃态节点,从而再次受到关注与新进的活跃态节点进行连接,这个过程称之为活化过程.网络的平均连接度则是由新进节点出度m决定的.
2 网络度分布的理论解析与数值模拟
设Ak′(t)为t时刻当前网络中具有入度为k′的活跃态节点的数目,Dk′(t)为t时刻当前网络中具有入度为k′的休眠态节点的数目.在网络随时间的演化过程中,可以分别写出活跃态和休眠态节点的差分方程.
对于活跃态节点有
(1)
对于休眠态节点有
(2)
其中μk′(t)为t时刻入度为k′的休眠态节点被活化的数目.由于每次均活化一个休眠态节点,因此μk′(t)的数值与当前网络中入度为k′的休眠态节点被活化的概率一致.νk′(t)为t时刻入度为k′的活跃态节点被老化概率.其中,(1)式右边第1项考虑了所有可能的没有被选择进行老化情况:1)当前入度为k′-1的活跃态节点被随机选出,被新进节点连接,并且没有被选择进行老化;2)当前入度为k′的活跃态节点没有被随机选出,并且没有被选择进行老化;3)当前被活化的入度为k′休眠态节点,并且没有被选择进行老化.
当网络规模足够大时,网络中活跃态节点的度分布趋于稳定状态,则有稳态条件∂Ak′(t)/∂t=0,代入(1)式可得
(3)

(4)
在该网络模型中,考虑了休眠态节点的随机活化情况,即当前每个休眠态节点被活化的概率是相同的,即休眠态节点j被活化的概率为
(5)
因此,可以得到当前t时刻入度为k′的休眠态节点被活化的数目为
(6)
应用大规模网络极限条件,从(6)式中可以得到
μk′=pk′.
(7)
该活化机制优化了原有的钝化网络模型在描述引文网络时所考虑的绝对老化情况.虽然活跃的论文可能会逐渐失去活性慢慢休眠,但其中一些已经休眠了不活跃的论文,还是有可能被引用从而重新回到人们的视野中来.
在网络的演化过程中,将活跃态节点的老化概率采用入度偏好的方式进行处理,即
(8)
将式(4),(7)和(8)式分别带入(3)式中进行约化得到
(9)
对上述方程进行求解得到
(10)
由于该网络模型的入度分布可以表示成活跃态节点的变化率,故有
(11)
(12)
因此,整个网络的入度分布为
(13)
由于k=k′+m,该网络中节点的度分布可以表示为
(14)
(15)
由上式可知,该网络度分布的衰减指数τ依赖于活跃态节点数M、节点的出度m和初始吸引子α的取值.图1a给出了生成网络参数为M=m,α=m+2,网络规模为105的整个网络度分布的数值模拟和拟合结果.图中的点表示数值模拟结果,实线对应于(14)式的最小二乘法的拟合结果.当m=10,20和40时,得到对应衰减指数的拟合结果分别为3.46(7),3.18(8)和3.00(8),而利用公式得到的理论解析衰减指数τ=3.图1b给出了M=5m,α=m-1.2,网络规模为105的整个网络度分布的数值模拟和拟合结果.此时,理论解析衰减指数τ=3.当m=10,20和40时,对应衰减指数的拟合结果分别为3.28(6),3.12(5)和2.99(7).比较可得,该网络模型度分布的数值模拟拟合结果随着m的增大与理论结果逐步趋于一致.
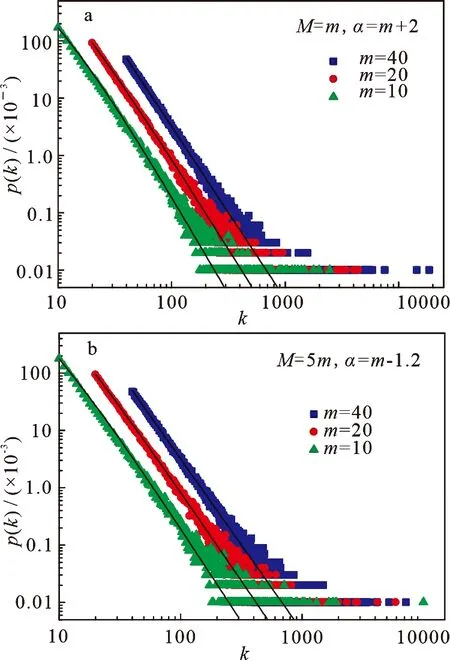
图1 生成网络的度分布的数值模拟和理论解析结果的比较
3 实证引文网络分析
为了对当前模型进行实证研究,从科学引文网络中找出了3组实证数据进行了对比.这3组实证数据分别是
1)PNAS data:该数据来源于1998年到2007年在美国国家科学院院刊(PNAS)上发表的文章,其中包含23572篇文章和40853篇引用文章[23];
2)Hep-ph data:该数据同样来源于arxiv.org网站上的预印本,覆盖了从1992年1月到2003年4月期间总计127个月的文章数据,共包含了34546篇文章和421578篇引用文章[24];
3)Hep-th data:该数据来源于arxiv.org网站上的预印本,覆盖了从1992年1月到2003年4月期间总共127个月的文章数据,共包含了27770篇文章和352807篇引用文章[24].
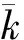

表1 3个实证网络的度统计数据和生成网络参数
利用表1中的数据,给出了科学引文网络实证数据的累积入度分布和生成网络的数值模拟结果的比较,如图2所示.可以看到,实证科学引文网络的实证数据与该模型的数值模拟结果吻合较好.

图2 生成网络的度分布的数值模拟和理论解析结果的比较
4 结束语
文中提出了一个广义的带有随机活化机制的钝化网络模型,该模型中节点的状态分为活跃态和休眠态,只有活跃态的节点有可能收到新进节点的连边.整个网络的增长动力学过程受控于节点状态的转变.研究发现,每篇论文的平均引文数量m、当前可选的论文数目M和不同科学领域的初始吸引子α决定了所生成网络的拓扑结构.如果M和α的取值分别为M=m,α=m+2时,网络节点度分布为衰减指数为τ=3的无标度分布.为了对当前模型进行验证,比较了科学引文网络中的3组实证数据,并且得到了与实证数据相一致的数值模拟结果.
