线性微分方程亚纯解的Baker游荡域
2023-01-10童英,龙芳,王珺
童 英,龙 芳,王 珺
(1. 上海市市北初级中学, 上海 200070; 2. 江西省机械高级技工学校 基础课部,江西 南昌 330013; 3. 复旦大学 数学科学学院, 上海 200433)
本文采用Nevanlinna理论的标准记号,该理论的基本概念和定义详见文献[1-3]。本文中,亚纯函数f(z),z∈均指在复平面上的亚纯函数,我们用T(r,f)和m(r,f)分别表示f的特征函数和均值函数,f的下级μ(f)和关于∞的亏量δ(∞,f)分别定义为
这里的log泛指对数运算。我们用fn表示f的n次迭代,其中n为正整数,f1(z)=f(z),f2(z)=f(f(z)),…,fn(z)=f(fn-1(z))。f的Fatou集F(f)为迭代函数族{fn}的正规区域,J(f)为F(f)的余集。Fatou集的连通分支简称为Fatou分支。假设U为f的Fatou分支,显然fn(U)必然包含在某个Fatou分支Un中。如果所有的Un均不相同,则称U为f的游荡域。有理函数没有游荡域,但是超越亚纯函数可能具有游荡域。例如,f(z)=z+sinz+2π有一有界单连通的游荡域,见文献[4]。Baker[5-6]给出过多连通游荡域的例子,这样的多连通游荡域后来被称为Baker游荡域。为了读者阅读的方便,我们下面介绍其定义。
定义1[5-6]假设U为f的游荡域。如果所有的Un均为F(f)的多连通分支,围绕着原点,且当n→∞时,Un与原点的欧式距离趋于无穷,则U被称为f的Baker游荡域。
Baker游荡域的存在性方面有一些已知的判定准则。例如,整函数f存在一有穷的Nevanlinna亏值或在一条到∞的路径上有界,则f没有Baker游荡域,见文献[7-8]。对于有理系数的一般线性微分方程。Zheng[9]证明了每个超越亚纯解都没Baker游荡域,并且其Julia集有无界分支。当方程系数超越且具有类似于指数函数的径向增长和衰减性质时,文献[10]给出判断线性微分方程的整函数解是否具有Baker游荡域的方法。
我们想通过方程系数的超越方向来确定解是否有Baker游荡域。我们先介绍超越方向的定义,然后给出具体的结果。
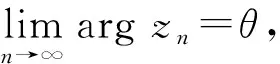
我们称θ为f的超越方向,f的所有超越方向所构成的集合记为TD(f)。
定理1假设超越亚纯函数A(z)满足[0,2π]
f(m)+A(z)f=0m≥2
(1)
的任一至多有有限个极点的非零亚纯解f及其n阶导数f(n)都没有Baker游荡域。

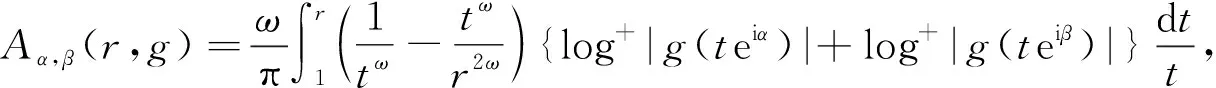
其中: g为g(z)的简写;bv=|bv|eiβv是g在Ω(α,β)闭包里的极点(按重数计);正对数log+x=max{lnx,0}。则g在Ω(α,β)上的特征函数为
Sα,β(r,g)=Aα,β(r,g)+Bα,β(r,g)+Cα,β(r,g)。
引理1[11]假设g(z)在Ω(α-ε,β+ε)上亚纯,其中0<α<β<2π,ε>0。则存在常数K>0,使得
对于r∉F成立,其中集合F具有有穷线性测度。
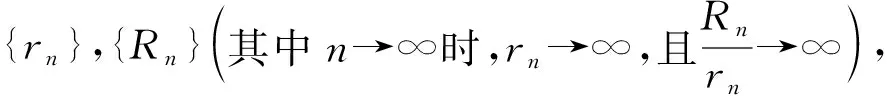
M(r,a,f)d≤L(r,a,f)r∈G。
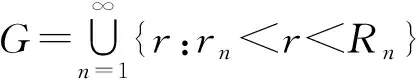
引理3[12]假设pj(x),j=1,2,…,n和f(x)为|a,b|上的复值函数,Pj(x),j=1,2,…,n和F(x)为定义在[a,b]上的非负连续函数且满足|pj(x)|≤Pj(x),|f(x)|≤F(x)。如果v(x)和V(x)分别满足微分方程
且|v(k)(a)≤V(k)(a),k=0,1,2,…,n-1,则成立|v(k)(x)|≤V(k)(x),x∈[a,b)。
下面我们来证明定理1。
首先将式(1)改写为-A(z)=f(m)/f,A超越必然推出f只能为超越解。由于δ(∞,A)>0,我们有δ(∞,A)T(r,A)≤m(r,A)。利用对数导数引理,显然存在常数M>0,使得
(2)
虽然当f的级为无穷时,对数导数引理中给出的估计有一线性测度有穷的集合,但考虑到文献[13]中的Lemma1.1.1,只需将式(2)中的T(r,f)换成T(αr,f),α>1即可,注意到A和f都是超越的,式(2)意味着μ(f)=∞。
因为f至多有有穷多个极点,从而存在r0>0,使得f在|z|≥r0内无极点。接下来,我们用反证法来说明g(z)=f(n)(z),n≥0没有Baker游荡域。假设g(z)有Baker游荡域,由文献[9]的Remark(A): 仅具有有穷多个极点的超越亚纯函数。其Julia集只有有界分支当且仅当该函数存在Baker游荡域,所以J(g)的所有分支均有界。从而由引理2可得: 存在常数d∈(0,1),使得
|g(z)|≥M(r,g)dr∈G0,
(3)
其中: 集合G0具有无穷对数测度。
情形1n=0。对于任意给定的θ∈[θ1,θ2],令h(r)=f(reiθ),则对于任意正整数k,h(k)(r)=eikθf(k)(reiθ)。将其代入方程(1)可得
h(m)+A(reiθ)eimθh=0。
(4)
对于正整数l≥2,通过简单计算可知(erl)(k)=pk(l-1)(r)erl,其中pk(l-1)(r)是关于r的k(l-1)次多项式,最高次项为lkrk(l-1)。令
取l=[τ]+2(≥2),其中[τ]为不超过τ的整数,定义V(r)=M0erl。不难验证
并且V(r)满足
V(m)-r[τ]+1V=F(r)。
(5)
对式(4)和式(5)运用引理3,我们得到
|f(reiθ)|=|h(r)|≤V(r)=M0ert
(6)
在Ω(r0,θ1,θ2)上都成立。结合式(3)和式(6),容易看出
M(r,f)d≤|f(z)|≤M0erlr∈G1=G0∩[r0,+∞],
其中集合G1也具有无穷对数测度,这意味着m(r,f)=O(rl),r∈G1,因为f至多有有穷多个极点,所以T(r,f)=O(rl)+O(logr),r∈G1。由此推出μ(f)≤l,这与μ(f)=∞相抵触。因此f没有Baker游荡域。
情形2n>0。由式(6)不难得到
Aθ1,θ2(r,f)=O(rl-ω),Bθ1,θ2(r,f)=O(rl-ω),
(7)
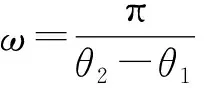
Sθ1,θ2(r,f)=Aθ1,θ2(r,f)+Bθ1,θ2(r,f)+Cθ1,θ2(r,f)=O(rl-ω)。
(8)
利用引理1,对于任意的ε>0,我们知道
(9)
例外集F1只有有穷的线性测度。当n=1时,由式(8)与式(9)我们可推出
对于r∉F1均成立。从而
以此为基础,利用类似的推导,我们可知: 对于r∉F1且n≥2时,
(10)
另一方面,根据式(3),我们知道: 对于α<β,
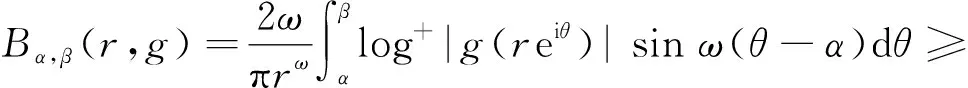
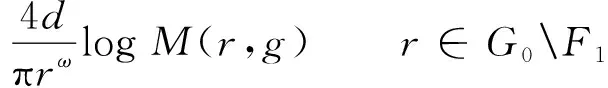
将式(10)代入可推出
从而m(r,g)=O(rl),r∈G0F1。注意到g的极点为有穷多个,所以μ(g)≤l。因为μ(g)=μ(f(n))=μ(f)=∞,这是矛盾的,故f(n)不存在Baker游荡域。
