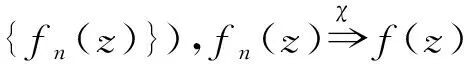涉及例外函数列的正规定则
2023-01-10陈巧玉周武能戚建明童东兵
陈巧玉,周武能,戚建明,童东兵
(1. 东华大学 信息科学与技术学院,上海 201620; 2. 上海工程技术大学 数理与统计学院,上海 201620; 3. 上海电机学院 商学院,上海 201306; 4. 上海工程技术大学 电子电气工程学院,上海 201620)
1 基础知识
记D是内的一个区域。在Montel意义下,亚纯函数族F在D内称为正规,若对F内的任意序列{fn(z)}都包含一个子序列{fnj(z)},该子序列在D的紧子集内按球面度量内闭一致收敛于一个亚纯函数f(z)或恒等于无穷。在D内即在D的紧子集内{fn(z)}按球面距离内闭一致收敛于f(z),fn(z)⟹f(z)于D,若收敛是在欧式度量下。Δ(z0,r)={z: |z-z0|
众所周知,涉及例外函数的亚纯函数族的正规定则的研究结果非常丰富。
2005年,Pang等[1]研究了涉及例外函数的亚纯函数族的正规定则,证明了如下结果。
定理A([1,定理1.1])设F是D内的亚纯函数族,其零点和极点均为重级。a(z)(≠0)是D内的亚纯函数。若对于任意f∈F,f′(z)≠a(z),则F在D内正规。
上述结果被Xu[2]推广到如下的高阶导函数。
定理B([2,定理1])设F是D内的亚纯函数族,其零点的重级至少为k+1且极点均是重级的,k∈+。a(z)(≠0)是D内的亚纯函数。若对于任意f∈F,f(k)(z)≠a(z)于D,则F在D内正规。
2007年,Nevo[3]证明了如下涉及例外函数列的结果。
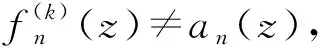
2013年,我们对涉及例外函数列的正规定则做了改进[4],且相关结果已被推广到高阶导函数[5]。
定理D[4]设{fn(z)}与{an(z)}是D内的两个亚纯函数列。{fn(z)}的零点和极点的重级均至少为k+2,{an(z)}的极点重级至少为k+1,k∈其中a(z)(≠0)是D内的亚纯函数。若则{fn(z)}在D内正规。
特别地,我们得到如下结果。
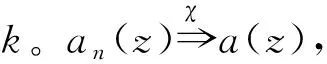
例1表明当k=1时,涉及例外函数列的正规定则与涉及例外函数的正规定则之间有着本质的区别。
例1设{fn(z)}与{an(z)}是Δ内的两个亚纯函数列,其中
显然,fn(z)的极点与an(z)的极点不同且
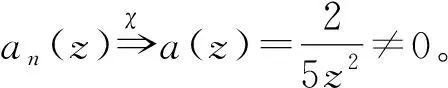
此外,例1也表明当k=1时,特别地,在定理E中,{fn(z)}中函数的零点重级的条件不能减弱。
接下来的例2揭示了定理E中的条件a(z)≠0在k=1时不能省略。
例2设{fn(z)}与{an(z)}是Δ内的两列亚纯函数,其中
显然,fn(z)有唯一一个重级为2的极点和两个重级为3的零点。an(z)⟹a(z)=z3,a(z)在Δ内有一个零点(z=0)。从而
但是,{fn(z)}在z=0不正规。
一般地,当定理D中{an(z)}的极点重级至少为k+1的假设去掉或减弱时,我们并不清楚相应的结果是否正确。本文主要研究当定理D中“{an(z)}的极点重级至少为k+1”的条件减弱为“{an(z)}的极点重级至少为k”时,在移除不正规点的区域内涉及例外函数列的亚纯函数列的特征。在这个减弱的条件下,我们证明了如下的结果,其表明亚纯函数列{fn(z)}的极限函数在某种程度上是唯一确定的。
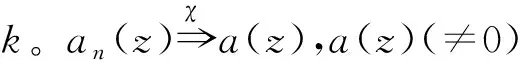
注1根据定理C,可知,定理1的条件“{fn(z)}的任意子列在z0∈D不正规”中的点z0在集合a-1(∞)内,即z0∈a-1(∞)。
2 辅助结果
为了证明定理,我们需要如下引理。
引理1([4,引理3.1])k次多项式在内取两个互异的有限值至少k+1次,k∈+。
引理2([6,引理12])设R(z)是不恒为常数的有理函数。若在内,R′(z)≠0,则或者R(z)=az+b,其中a≠0,b,c∈,n∈。
引理3([7,定理1])设f(z)与R(z)(≠0)分别是内的超越亚纯函数与有理函数。若f(z)的零点重级至少为k+1(除了有限多个外),则f(k)(z)-R(z)在内有无限多个零点。
引理4([8,引理2.3])设{fn(z)}与{an(z)}是D内的两列亚纯函数,f(z)与a(z)是D内的两个亚纯函数。若
则f(k)(z)≠a(z)或者f(k)(z)≡a(z)。
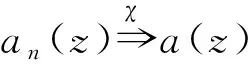
根据文献[2,定理1],[9,定理1’]的证明方法及结合定理C和引理5,可以得到如下引理(见文献[8,引理2.10];[10,引理3.8])。
引理6[8,10]设{fn(z)}与an(z)是D内的两个亚纯函数列。{fn(z)}的零点重级均至少为k+1且{fn(z)}的极点均为重级的,k∈于D,其中a(z)(≠0)是D内的亚纯函数。an(z)与a(z)有相同的极点且重级也相同。若则{fn(z)}在D内正规。
3 辅助引理
为了证明定理1,先证明下面的引理。
引理7设R(z)是不恒为常数的有理函数。若在内R(k)(z)≠0,则
(1)
其中:m=n或者m=n+1,n≥k,k∈+;A≠0;αi(1≤i≤m),β∈。
证 显然,(R(k-1)(z))′≠0。所以,R(k-1)(z)是不恒为常数的有理函数。根据引理2,得
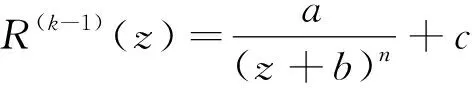
其中:n≥k,k∈+;a(≠0),b,c∈。则
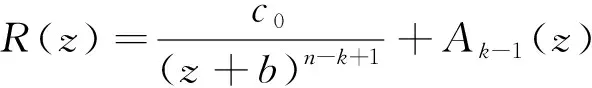
其中:Ak-1(z)与Ak(z)分别为k-1次与k次多项式;c0∈。则R(z)有如下形式:
其中:m=n或者m=n+1,n≥k,k∈+;A≠0;αi(1≤i≤m),β∈。因此,引理7得证。
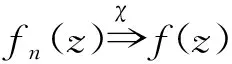
(i) {fn(z)}的任意子列均在z=0不正规,
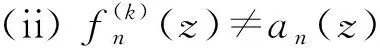
则在Δ内f(z)是亚纯函数且f(k)(z)≡a(z)。
证 假设f(k)(z)≢a(z)于Δ′。根据引理4,得f(k)(z)≠a(z)。取δ>0,使得Δ2δ⊂Δ且f(z)在∂Δδ上无极点。则存在A>0,使得在∂Δδ上,有|f(k)(z)-a(z)|≥A。
设fn(0)≠∞。(若不然,取zn→0满足fn(zn)≠∞,考虑用函数fn(zn+z)与an(zn+z)替代fn(z)与an(z)。)
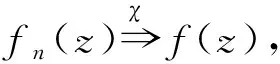
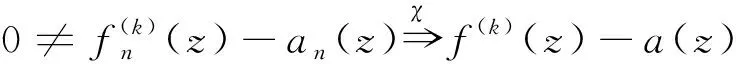
从而,对充分大的n,
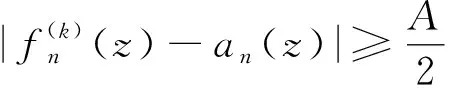
可得
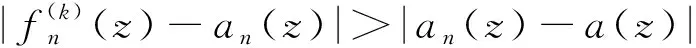
因此,根据亚纯函数的Rouché定理([11],p.121),有
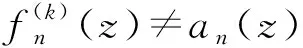
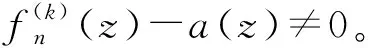
引理9设{sn}是一个数列且0≠sn→0,{fn(z)}是Δ内的亚纯函数列,其零点和极点的重级均至少为k+2,{an(z)}是Δ内的亚纯函数列。假设
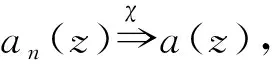
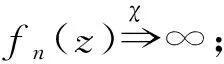
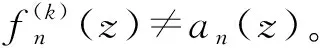
证 假设,若不然,则P(z)≢0且P(z)至少有1个重级不小于k+2的零点。
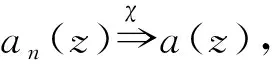
因此,
(2)
其中:λ(z)是最高项系数为1的多项式;A是非零常数。若P(z)≠∞,根据方程(2),得P(z)≡0,与假设矛盾。
因此,令
(3)
其中:B是非零常数;m≥1,n≥1;ai(i=1,2,…,m)是P(z)在内的零点;bj(j=1,2,…,n)是P(z)在内的极点;αi≥k+2,βj≥k+2是整数,
因此,
(4)
其中:g(z)=B(M-N)(M-N-1)…[M-N-(k-1)]zk(m+n-1)+…+a0是次数不超过k(m+n-1)的多项式;a0是常数。
根据方程(2)和(4),有
(5)
(6)
断言:N+w=M(0≤w≤k-1)或者N-M=t-k。事实上,假设N+w≠M,则deg(g(z))=k(m+n-1)。根据方程(6),得N-M=t-k。因此,断言成立。
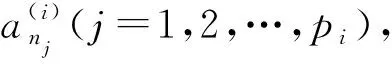
令
(7)
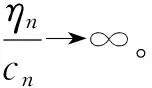
Φn(z)=(ηn)t-kfn(ηnz)z∈ΔRn,Rn→∞。
(8)
因此
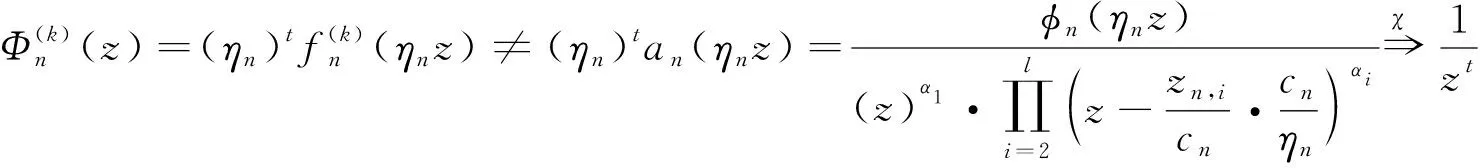
根据定理C,得{Φn(z)}在0}正规。假设于0}。根据Φn(1)=0,得Φ(z)≢∞。
因为
且由方程(7)和(8),有

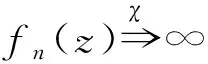
根据方程(2)—(4),有
,
其中:
deg(g(z))=N-M+k(m+n)-t。
(9)
根据方程(5),(6)和(9)及引理1,得

从而,n+m(k+1)≥M+1。
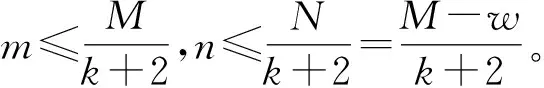
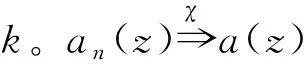
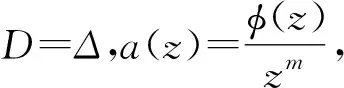
下面,对z=0的重级m作数学归纳,证明{fn(z)}在z=0正规。
首先,考虑m=k,则l=1。根据引理6,结论成立。
其次,在假设当m
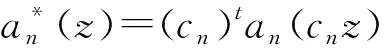
显然,
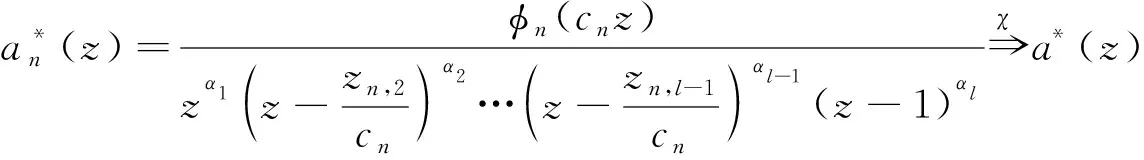
其中:a*(z)∈是至少有两个极点0与1的亚纯函数。则a*(z)的所有极点重级都小于t。
根据定理C,{Pn(z)}在
断言A: 对于充分大的n,存在δ>0,满足fn(z)≠0于Δδ。若不然,存在ξn∈Δ,ξn→0,{fn(z)}的一个子列(仍记为{fn(z)}),使得fn(ξn)=0。假设ξn是fn(z)的模最小的零点。
下面分如下两种情况进行讨论。
情形ⅠP(z)≠0。
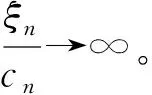
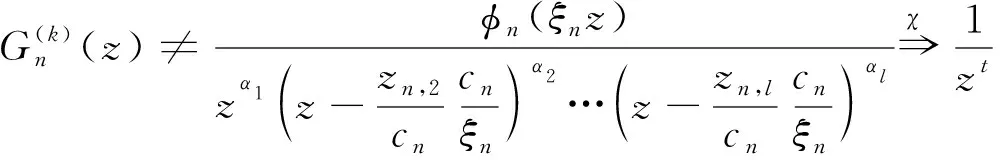
根据定理C和引理5,得{Gn(z)}在内正规。假设于。根据引理9,得在内G(z)≠0或者G(z)≡0。由Gn(1)=0,可得在内G(z)≡0,这与矛盾。
情形ⅡP(z)≡0。
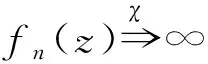
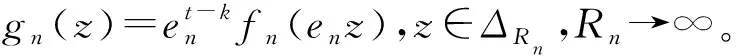
从而
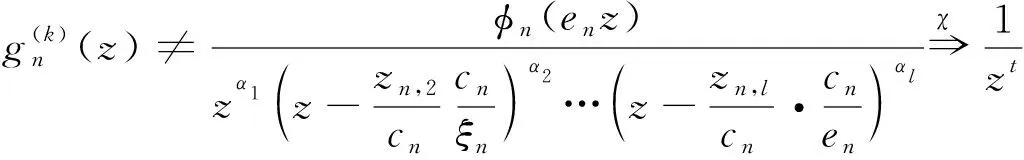
根据定理C,得{gn(z)}在{0}内正规。
断言B1: {gn(z)}是Δ内的全纯函数;断言B2: {gn(z)}在z=0正规。
首先,证明断言(B1)是正确的。若不然,存在νn,0<|νn|<1,使得gn(νn)=∞。则ωn(νnen)=∞。因此,存在μn∈Δ满足0<|μn|<|νnen|<|en|,使得|ωn(μn)|=1,与en的选取矛盾。故,断言B1得证。
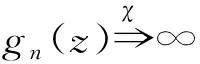
从而{gn(z)}在内正规。假设于。根据引理9,得在内g(z)≠0或者g(z)≡0。根据|g(1)|=1,得g(z)≠0。因为gn(ξn/en)=(en)t-kfn(ξn)=0,则ξn/en→∞。接下来的证明与情形Ⅰ类似。令Gn(z)=(ξn)t-kfn(ξnz),z∈ΔRn,Rn→∞。也能得出矛盾。
因此,断言A得证。根据引理5,得{fn(z)}在Δδ正规。从而,引理10得证。
4 定理1的证明