基于Rashba和Dresselhaus自旋轨道耦合的非均匀量子线中电子传输特性研究

陈 妍 刘 誌 黄 朵

（1.江西理工大学 电气工程与自动化学院，赣州 341000；2.江西理工大学 信息工程学院，赣州 341000）

目前，半导体中的自旋输运特性因其在未来自旋电子器件中具有巨大潜力而获得了人们越来越多的关注[1-2]。这个领域最重要的问题是如何提供可行的方法来产生、操作、存储和检测半导体材料中的自旋极化电子。由块体材料的反转不对称性引起的Dresselhaus自旋轨道耦合（Spin Orbit Coupling，SOC）和由结构反转不对称性引起的Rashba自旋轨道耦合，被认为是实现这些目标的手段。本文采用非平衡格林函数方法，结合Landauer-Büttiker近似，研究基于Rashba和Dresselhaus两种自旋轨道耦合的非均匀量子线中的自旋输运性质。

1 模型与分析

研究的凹型非均匀量子线的结构如图1所示。Rashba和Dresselhaus自旋轨道耦合夹在两条正常的金属导线之间，如图1（a）所示。相应的实验装置方案如图1（b）所示。使用(x,y)平面上的二维电子气（Two-Dimensional Electron Gas，2DEG）来定义非均匀量子线。顶栅产生横向限制势V(x,y)用于描绘非均匀量子线后栅用于调谐Rashba自旋轨道耦合强度。非均匀量子线（Quantum Wire，QW）窄中心部分的宽度为D，长度为H，左右宽部分具有相同的长度L和相同的宽度W。量子线的左右两边都连接着宽度为W的半无限长理想导线。

为了研究系统的电子传输特性，将其离散成一个正方形晶格。在Rashba和Dresselhaus自旋轨道耦合上具有紧密约束的哈密顿量在正方形晶格上的定义为

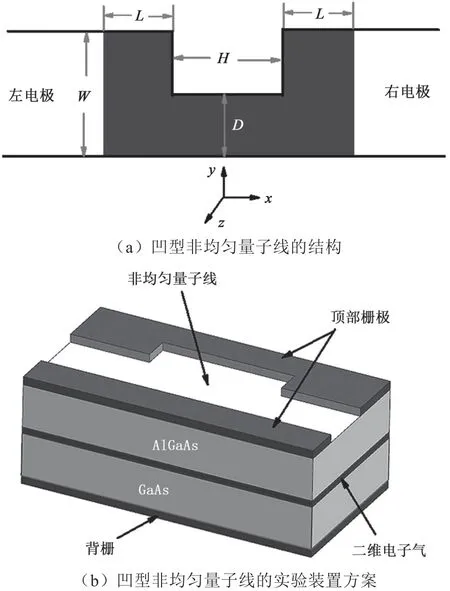
图1 “凹型”非均匀量子线的结构及实验装置图

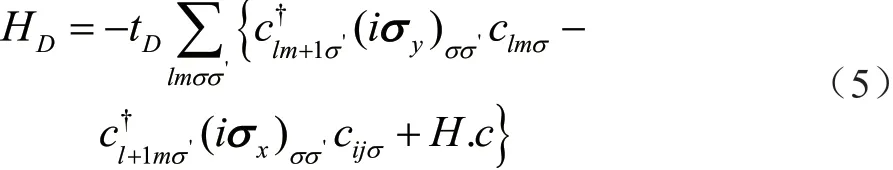
式中：HO为不含自旋轨道耦合时的哈密顿量；V为外加限制势能；HR为含Rashba自旋轨道耦合时的哈密顿量；HD为含Dresselhaus自旋轨道耦合时的哈密顿量为lm格点自旋σ（σ=↑,↓）的产生（湮灭）算符；σx和σy为泡利矩阵；εlmσ=4t为格点能，其中为格点之间的势能，这里 ħ =h/2π，h为普朗克常数；m*（m*=0.067me）和a分别为电子的有效质量和晶格常数；Vlm为格点上额外限制势；HR为Rashba自旋轨道耦合项；tR=α/2a为Rashba SOC强度，其中α为Rashba常数；HD为Dresselhaus SOC自旋轨道耦合项，tD=β/2a为Dresselhaus SOC强度，其中β为Dresselhaus常数；σ´为自旋方向，σ´=↑或↓；H.c.是公式中前两项的共轭项。

基于哈密顿量，用非平衡格林函数（Non-Equilibrium Green Functions，NEGF）可以得到散射电子态的出射波函数[3]。随后采用Landauer-Büttiker公式得到两端的自旋相关电导[4-5]，即

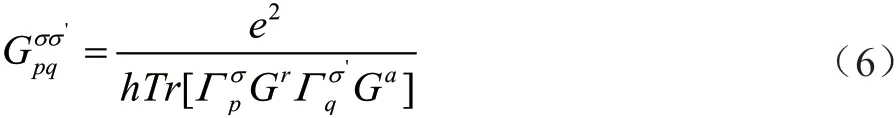
式中：e为电子电荷量；h为普朗克常数；左右两端导线引起的自能分别用和表示；Tr为对凹型非均匀量子线整个空间自由度求迹。另外，凹型非均匀量子线整个系统含有自能的推迟格林函数为Gr，而超前格林函数为Ga。

电子从左边入射端电极透射到右边出射端电极的概率在Z方向上的总电导定义为

由自旋极化电子输运引起的右边出射端局域自旋密度的变化在Z方向上的自旋极化率定义为

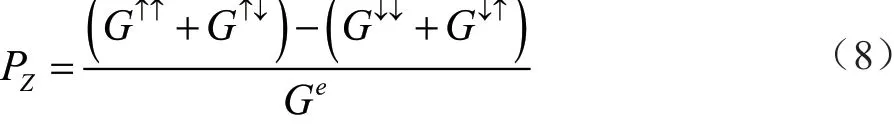
选择的物理量为具有典型电子密度即每平方厘米约为2.5×1011V·s的高迁移率GaAs/AlxGa1-xAs异质结结构[6]。所有能量都由跳跃能量t（t=1）归一化，量子线的其他参数固定为W=20a、D=7a、L=10a和H=30a，紧密结合模型的晶格间距设为a=1 nm。

2 结果和讨论

图2（a）为凹型非均匀量子线左侧部分的能量子带色散；图2（b）为凹型非均匀量子线右侧部分的能量子带色散，a-1为晶格常数的倒数（相当于单位），k为波数。Rashba SOC的强度设置为tR=0.158，Dresselhaus SOC的强度设置为tD=0.158。

E≥0.154 1 meV，左 侧 部 分 具 有 一 个 子 带。E≥0.206 1 meV，右侧部分有两个子带。图3（a）为自旋向上（实曲线）和自旋向下（虚曲线）电子的电荷电导与能量的关系。图3（b）为与图3（a）相应的自旋极化率随电子入射能量的变化。可以看到，电荷电导呈阶梯状结构，且电导显示自旋向上电子和自旋向下电子之间的临界差异。当入射能量E=0.154 1 meV时，左（右）部分最低的一（两）对子带成为传播模。随后，Rashba和Dresselhaus自旋轨道耦合引起的子带混合导致非零的自旋极化电流。在对应右侧子带极小值的电子能量即E=0.154 1 meV处，获得了大的自旋极化|PZ|=0.63。

量子线中间较窄部分的能量子带发生色散。Rashba和Dresselhaus自旋轨道耦合的强度分别取为tR=0.158和tD=0.158。

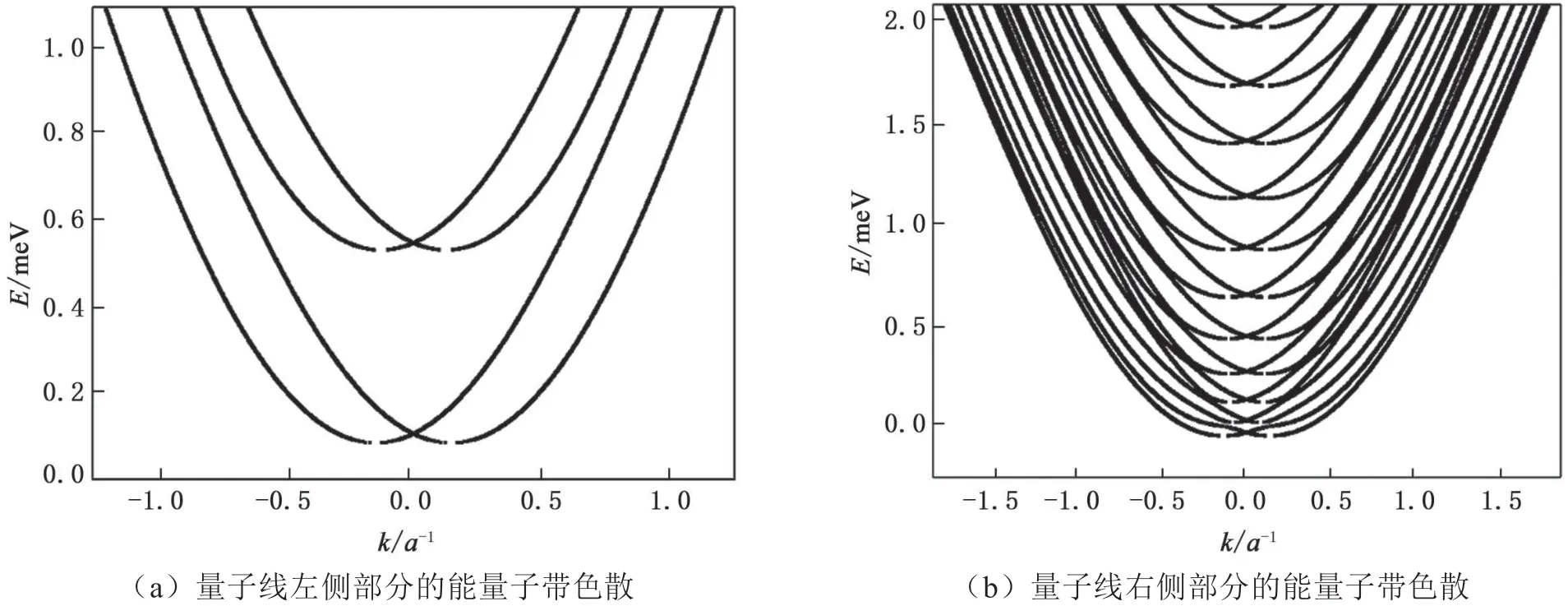
图2 “凹型”非均匀量子线能量子带色散

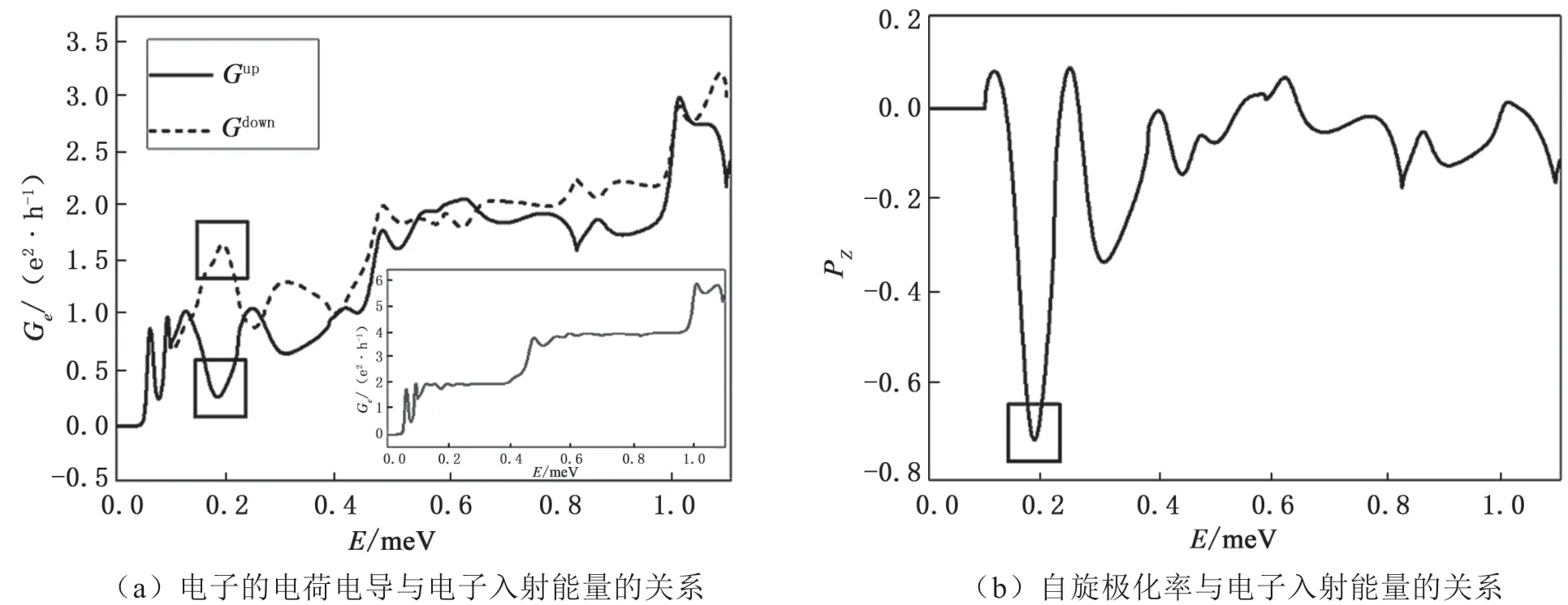
图3 电子入射能量的影响因素

如图4所示，Dresselhaus SOC强度tD=0.0（实曲线）、tD=0.108（虚曲线）和tD=0.158（点曲线）时，电子自旋极化率随入射能量变化，其中Rashba SOC强度设置为tR=0.158。

研究非均匀量子线相对于Rashba和Dresselhaus SOC的电子自旋极化。首先，研究Dresselhaus SOC对电子自旋极化的影响。如图4所示，对于tD=0.0时（即没有Dresselhaus SOC的情况），在入射能量E=0.206 1 meV时，观察到|PZ|=0.78的自旋极化值的峰值。当tD≠0.0（即包括两个SOC）时，仍然存在较大的电子自旋极化率。例如，即使当Dresselhaus SOC强度tD=0.158时，也表现出|PZ|的高自旋极化率，且在入射能量E=0.154 1 meV时可得到自旋极化率|PZ|=0.63。随着Dresselhaus SOC强度的增加，自旋极化曲线中的峰向左稍移，高度降低。这源于有效电位与Dresselhaus SOC之间的相互作用，也表明可以通过改变Dresselhaus SOC强度来调制自旋极化。

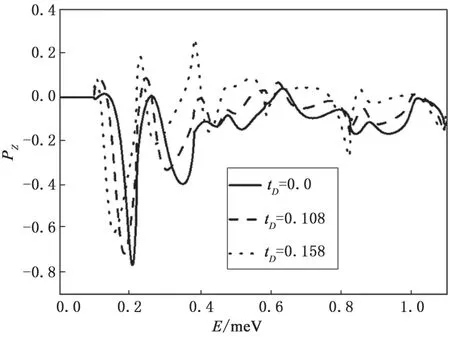
图4 电子自旋极化率随入射能量变化

对于自旋非极化电子注入，计算可得到自旋极化与Rashba和Dresselhaus SOC强度的函数关系，入射能量E=0.154 1 meV。

电子自旋极化值对SOC强度的设定值很敏感。为了进一步研究Rashba和Dresselhaus SOC的组合影响，研究不同强度的Dresselhaus和Rashba SOC在非均匀量子线中的电子自旋极化随入射能量E=0.154 1 meV的变化。如图5所示，当Dresselhaus SOC和Rashba SOC同时加入到非均匀量子线上时，电子自旋极化的等高线图表现为“圆形”分布，且具有基本相同的作用。

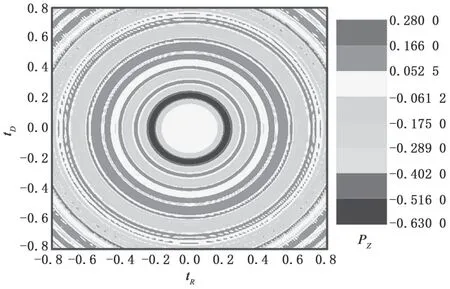
图5 电子自旋极化率的等高线图

3 结语

由于非均匀量子线的镜面对称性被破坏，即使同时存在Rashba和Dresselhaus SOC，仍然可以诱导出较大的电子自旋极化。此外，实验结果表明，系统的自旋极化随Dresselhaus和Rashba SOC的变化呈“圆形”分布，表明这两个SOC在诱导自旋极化方面起着基本相同的作用。因此，人们可以通过调制Rashba或Dresselhaus SOC强度来调节系统的自旋极化，从而使提出的结构可能在不使用任何磁性材料或施加磁场的情况下制造多功能半导体自旋电子器件。