例析立体几何中与垂直相关的探索性问题

何秋霞

(江苏省南京市高淳区湖滨高级中学)

立体几何中的探索性问题具有一定难度,而有关垂直的探索性问题是其中的一类.探索性问题大致可分为是否成立问题和是否存在问题.它们设问不同,但本质上都是探索性问题.笔者认为立体几何中与垂直相关的探索性问题可以分为如下两类:

1)是否成立问题——适合题设条件的结论是否成立,探索条件或位置.

2)是否存在问题——满足某条件时结论才能成立.

1 是否成立问题

判断一个命题是否成立,是较为简单的探索性问题.立体几何中常见的是否成立问题通常是以几何体为载体考查线线、线面、面面的位置关系,其中以垂直关系最具代表性.解决这类问题常用的思路有两种:1)先给出判断结果再证明或举反例.2)先假设结论成立再进行逻辑推导,若推导不出矛盾,则结论正确;若推导出矛盾,则结论错误.

例1如图1 所示,在四面 体PABC中,△PAC和△ABC均为等腰三角形,且∠APC＝∠BAC＝90°,PB＝AB＝4.判断AB⊥PC是否成立并给出证明.

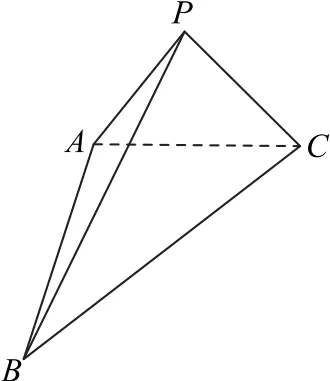
图1

解析已知AB⊥AC,欲判

断AB⊥PC是否成立,只需判断AB⊥AP是否成立.

经判断知AB⊥PC不成立,证明如下.

假设AB⊥PC,由∠BAC＝90°,有AB⊥AC,又PC∩AC＝C,PC⊂平面PAC,AC⊂平面PAC,所以AB⊥平面PAC,又AP⊂平面PAC,所以AB⊥AP,从而BP＞AB,这与PB＝AB矛盾,故假设不成立,即AB⊥PC不成立.

例2如图2所示,AB是圆O的一条直径,C是圆上不同于A,B的点,PA垂直于圆O所在平面,平面PAC与平面PBC是否一定垂直? 请说明理由.

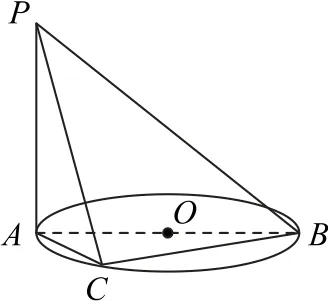
图2

解析判断面面是否垂直,就是寻找一个平面内有无一条直线垂直于另一个平面内的两条相交直线.

经判断知平面PAC⊥平面PBC.证明如下.

因为C在以AB为直径的圆周上(除A,B两点外),AC⊥BC,PA⊥平面ABC,BC⊂平面ABC,所以PA⊥BC.

又PA∩AC＝A,PA⊂平面PAC,AC⊂平面PAC,BC⊥平面PAC,而BC⊂平面ABC,所以平面PAC⊥平面PBC.

2 是否存在问题

是否存在满足某个条件的结论,一般称为存在性问题.立体几何中与垂直有关的存在性问题较为常见.

解决存在性问题的思路有三种:

1)先猜后证——先给出结论再证明满足条件,相当于找到使命题成立的充分条件,再证明命题成立.

2)先作后算——先作出符合条件的图形再由题设条件推导出结论,相当于承认命题成立,寻找命题成立的必要条件.

3)边作边证边算——一边应用条件作图,一边证明并计算.

2.1 探索线面垂直

探索线面垂直问题是探索与垂直有关问题的基础题目.可以将线面垂直转化为线线垂直,进而由线线垂直寻找探索点的位置.

例3如图3所示,直三棱柱ABC-A1B1C1的底面是等腰三角形,∠A1C1B1＝90°,A1C1＝1,AA1＝,D为A1B1中点.

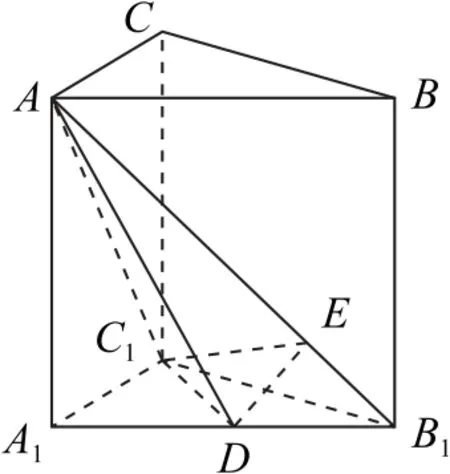
图3

(1)求证:平面AC1D⊥平面ABB1A1;

(2)在AB1上是否存在一点E,使得AB1⊥平面C1DE? 若存在,求出的值;若不存在,说明理由.

解析(1)可 证C1D⊥平 面ABB1A1(具体求解过程略).

2.2 探索面面垂直

面面垂直的本质仍是线面垂直,因此,探索面面垂直仍回到探索线面垂直.

例4如图4所示,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB＝1,BC＝2,CD＝1＋,过A作AE⊥CD,垂足为E.现将△ADE沿AE折起使得DE⊥EC,如图5所示,问:在线段AE上是否存在一点F,使得平面BDF⊥平面BDC? 若存在,指出F的位置;若不存在,说明理由.

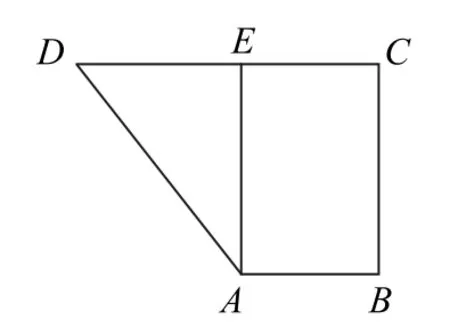
图4

图5

解析方法1假设在线段AE上存在点F,使得平面BDF⊥平面BDC.由DE⊥EC,DE＝,EC＝1,得DC＝2＝BC,取BD的中点M,连接CM,FM,FC,则CM⊥BD,如图6所示.

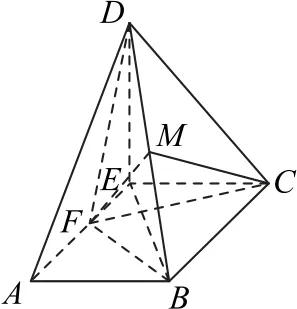
图6

因为平面BDF⊥平面BDC,CM⊥BD,CM⊂平面BDC,平面BDF∩平面BDC＝BD,所以CM⊥平面BDF,又FM⊂平面BDF,所以CM⊥FM.因为DE⊥EC,DE⊥AE,AE∩EC＝E,所以DE⊥平面ABCE,DE⊥EB.

方法2假设在线段AE上存在点F,使得平面BDF⊥平面BDC.延长BC于N,使得BC＝CN＝2,连接DN,如图7 所示,由＝1,得DC＝2,则DN⊥DB.因为DE⊥EC,DE⊥AE,AE∩EC＝E,所以DE⊥平面ABCE,DE⊥EB.

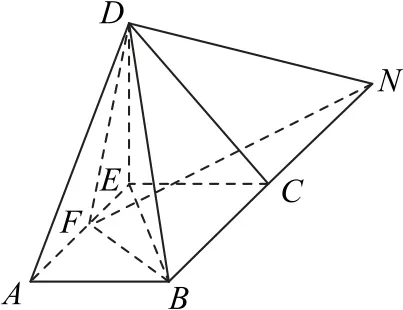
图7

探索性问题分散在立体几何的各模块之中,考查思维的灵活性,综合考查逻辑推理素养、运算求解能力、空间想象素养、分类讨论思想等.

(完)