构造长方体模型解一类特殊的四面体问题
2023-01-07李勇
李 勇
(贵州省贵阳市息烽县第一中学)
对棱相等的四面体是一类特殊的三棱锥,根据三对棱的长度关系,可以把它放在对应的长方体、正四棱柱以及正方体中,进而解决有关问题.
1 长方体模型
在四面体A-BCD中,若AB=CD,BD=AC,AD=BC,则可把四面体A-BCD放在长方体中进行研究,进而解决有关问题.
例1在三棱锥A-BCD中,AB=CD=2,AD=BC=3,AC=BD=4,求三棱锥A-BCD的外接球的体积.
解析如图1 所示,把三棱锥A-BCD放在长方体AECF-HDGB中,设HB=x,HD=y,HA=z,则可得方程组
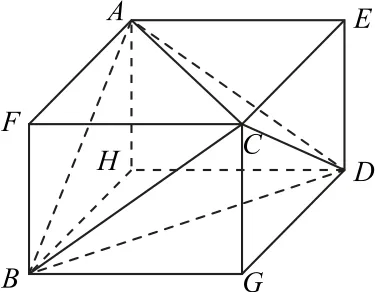
图1

点评本题如果用传统的解法:找球心,求半径来解,难度比较大.根据三棱锥的三组对棱的特点联想到长方体的面对角线,把该三棱锥放在长方体中,解决问题就简单多了.由于该三棱锥的外接球恰好就是长方体的外接球,因此问题转化为求长方体的外接球的体积.求解步骤如下:
第一步,根据三棱锥的棱长(即长方体的面对角线长)算出长方体的长、宽、高的关系(或长、宽、高的值),从而算出长方体的体对角线的长的平方.
第二步,根据长方体的性质(长方体的体对角线即为长方体外接球的直径),算出外接球的半径.
第三步,利用球的体积公式算出体积即可.
例2在三棱锥P-ABC中,PA=BC=,求平面APB与平面CPB的夹角的余弦值.
解析如图2所示,把三棱锥P-ABC放在长方体AECD-FPGB中,设PF=x,PG=y,PE=z,则CPB的夹角的余弦值为
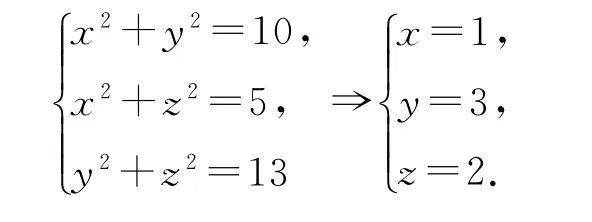
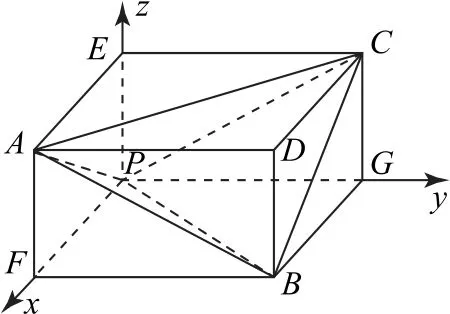
图2

点评本题如果用传统的求二面角的方法解答难度比较大,根据三棱锥的三组对棱的特点可联想到长方体的面对角线,把该三棱锥放在长方体中,用“坐标法”解答问题就简单多了.求解步骤如下:
第一步,根据三棱锥的棱长(即长方体的面对角线长)算出长方体长、宽、高的值.
第二步,建立空间直角坐标系,算出平面APB与平面CPB的法向量,求出两个法向量夹角的余弦值.
第三步,根据两个法向量夹角的余弦值写出平面APB与平面CPB的夹角的余弦值.
2 正四棱柱模型
在四面体ABCD中,若AB=CD=BD=AC,AD=BC,则可把四面体ABCD放在正四棱柱中进行研究,进而解决有关问题.
例3在三棱锥A-BCD中,AB=BC=CD=DA=3,AC=BD=2,M,N分别是AD,BC的中点,求异面直线AN,CM所成角的余弦值.
解析如图3所示,把三棱锥A-BCD放在正四棱柱AECF-HDGB中,设HB=x,HA=z,则

图3


点评本题是人教A 版《选择性必修第一册》中第41页的第2 题.从在书中的位置来看,本题应该用“向量法”解答,由于许多学生建不了系,故不能使用“坐标法”解答,运算量比较大.如果能根据三棱锥的三组对棱的特点联想到正四棱柱(即特殊的长方体)的面对角线,把该三棱锥放在正四棱柱中用“坐标法”解答就非常简单了.求解步骤如下:
第一步,根据三棱锥的棱长(即正四棱柱的面对角线长)算出正四棱柱的底面边长和高的值.
第二步,建立空间直角坐标系,写出异面直线AN,CM的方向向量,求出两异面直线AN,CM方向向量夹角的余弦值.
第三步,由两异面直线AN,CM方向向量夹角的余弦值写出异面直线AN,CM所成角的余弦值.
例4在三棱锥A-BCD中,AC=BD=,其余四条棱长均为2,则三棱锥A-BCD的外接球的表面积为_________.
解析如图4所示,把三棱锥A-BCD放在正四棱柱AECF-HDGB中,设HB=x,HA=z,则
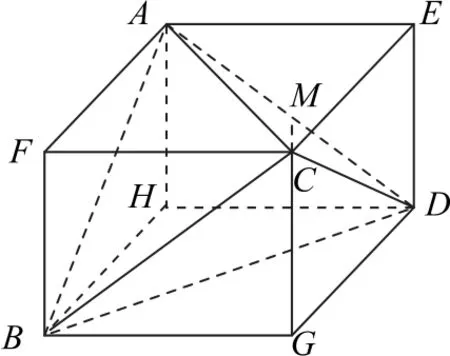
图4
由正四棱柱的性质可知4R2=x2+x2+z2=7,所以4πR2=7π,故三棱锥A-BCD的外接球的表面积为7π.
点评本题如果用传统的方法:找球心,求半径来解,难度比较大.联想到正四棱柱(即特殊的长方体)的面对角线,把该三棱锥放在正四棱柱中,解决问题就简单多了.由于该三棱锥的外接球恰好就是正四棱柱的外接球,因此问题转化为求正四棱柱外接球的表面积.求解步骤如下:
第一步,根据三棱锥的棱长(即正四棱柱的面对角线长)算出正四棱柱的底面边长和高的值.
第二步,算出正四棱柱的体对角线的长的平方,即外接球直径的平方.
第三步,根据球的表面积公式即可求出三棱锥A-BCD的外接球的表面积.

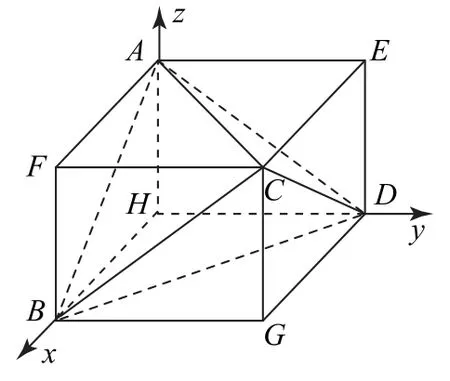
图5
点评本题可根据三棱锥三组对棱的特点联想到正四棱柱(即特殊的长方体)的面对角线,把该三棱锥放在正四棱柱中,用“坐标法”解答问题就非常简单了.求解步骤如下:
第一步,根据三棱锥的棱长(即正四棱柱的面对角线长)算出正四棱柱的底面边长和高的值.
第二步,建立空间直角坐标系,算出平面ABC的法向量.
第三步,在平面ABC上任意取一点与外接球的球心构造一个向量.
第四步,代入点到平面的距离公式,即可算出三棱锥A-BCD外接球的球心到平面ABC的距离.
3 正方体模型
在四面体ABCD中,若AB=CD=BD=AC=AD=BC,则可把四面体ABCD放在正方体中研究,进而求解相关问题.
例6已知四面体OABC的所有棱长都是1,D,N分别是OA,BC的中点.
(1)计算DN的长度;
(2)求点O到平面ABC的距离.
解析如图6所示,把四面体OABC放在正方体中.设正方体的棱长为a,则a2+a2=1,所 以
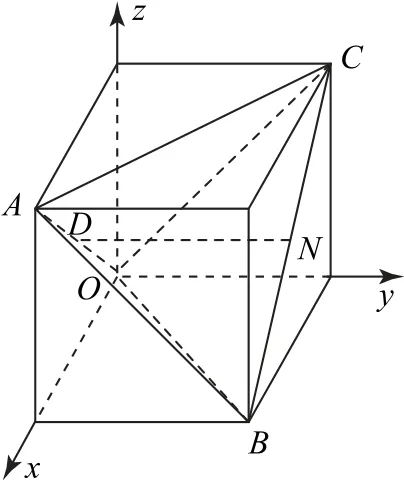
图6


点评本题是人教A 版《选择性必修第一册》中第42页的第7题,从在书中的位置来看,本题应该是用“向量法”来解答,只是大部分学生可能只会在正四面体中建系,运算难度较大.如果能根据三棱锥的三组对棱的特点联想到正方体(即特殊的长方体)的面对角线,把该三棱锥放在正方体中,解决问题就简单多了.求解步骤如下:
第一步,根据三棱锥的棱长(即正方体的面对角线长)算出正方体棱长的值.
第二步,建立空间直角坐标系,写出点的坐标,算出DN的长度和平面ABC的法向量.
第三步,在平面ABC上任意取一点与点O构造一个向量.
第四步,代入点到平面的距离公式算出点O平面ABC的距离.
例7已知正四面体ABCD的外接球的体积为,则该四面体的表面积为_________.
解析把正四面体ABCD放在如图7 所示的正方体中.设正四面体ABCD的外接球的半径为R,正四面体ABCD的棱长为x,正方体为棱长为y,则
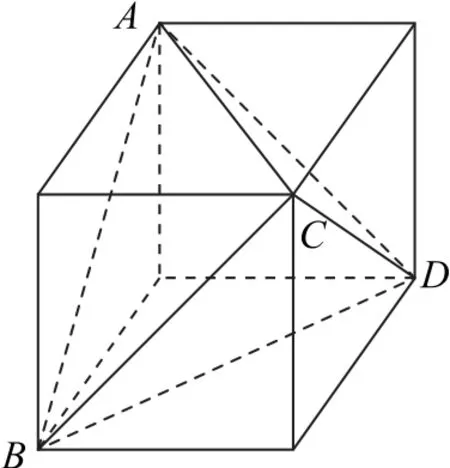
图7
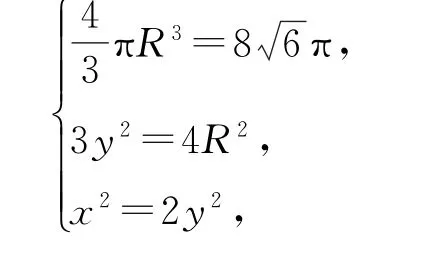
解得x2=16,故正四面体ABCD的表面积为
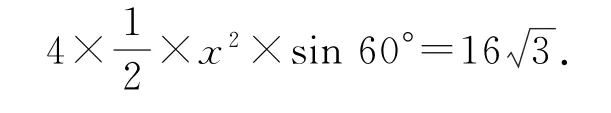
点评根据三棱锥的三组对棱的特点联想到正方体(即特殊的长方体)的面对角线,把该三棱锥放在正方体中,进而解决该题.求解步骤如下:
第一步,根据正四面体的外接球的体积算出正方体棱长的平方.
第二步,代入面积公式即可求出这个正四面体的表面积.
例8正四面体ABCD中,,点P在棱AB上运动,设EP与平面BCD所成角为θ,则sinθ的最大值是( ).

解析如图8所示,把正四面体ABCD放在正方体中,建立空间直角坐标系.设正方体的棱长为1,则A(0,0,1),B(1,0,0),C(0,1,0),D1(1,1,0).
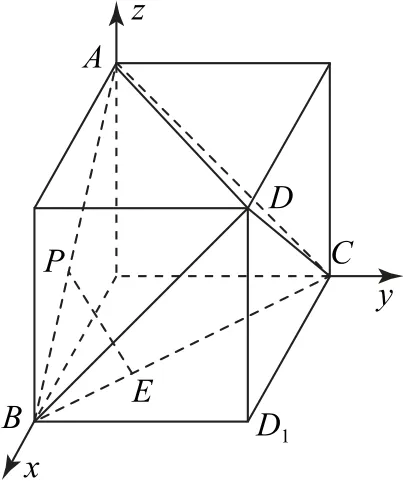
图8

点评本题有一定的难度,但是把该三棱锥放在正方体中用“坐标法”解答就简单多了.求解步骤如下:
第一步,建立空间直角坐标系,设正方体的棱长为1,并写出点的坐标,求出平面BCD的法向量.
第二步,由点P在棱AB上运动,设(0≤λ≤1),求出的坐标.
第三步,代入线面角公式求出sinθ的最大值.
总之,可根据对棱长的特点,把图形放入长方体、正四棱柱、正方体中解答这类问题.通过构造可以降低思维难度,减少运算量,能很好地体现数学核心素养中的直观想象、数学建模、数学运算,有利于拓展学生思维,有利于培养数学核心素养.
(完)
