强基计划数学备考系列讲座(11)
——立体几何求解与证明路径
2023-01-07王慧兴
王慧兴
(清华大学附属中学)
1 知识与技能
1.1 要点梳理
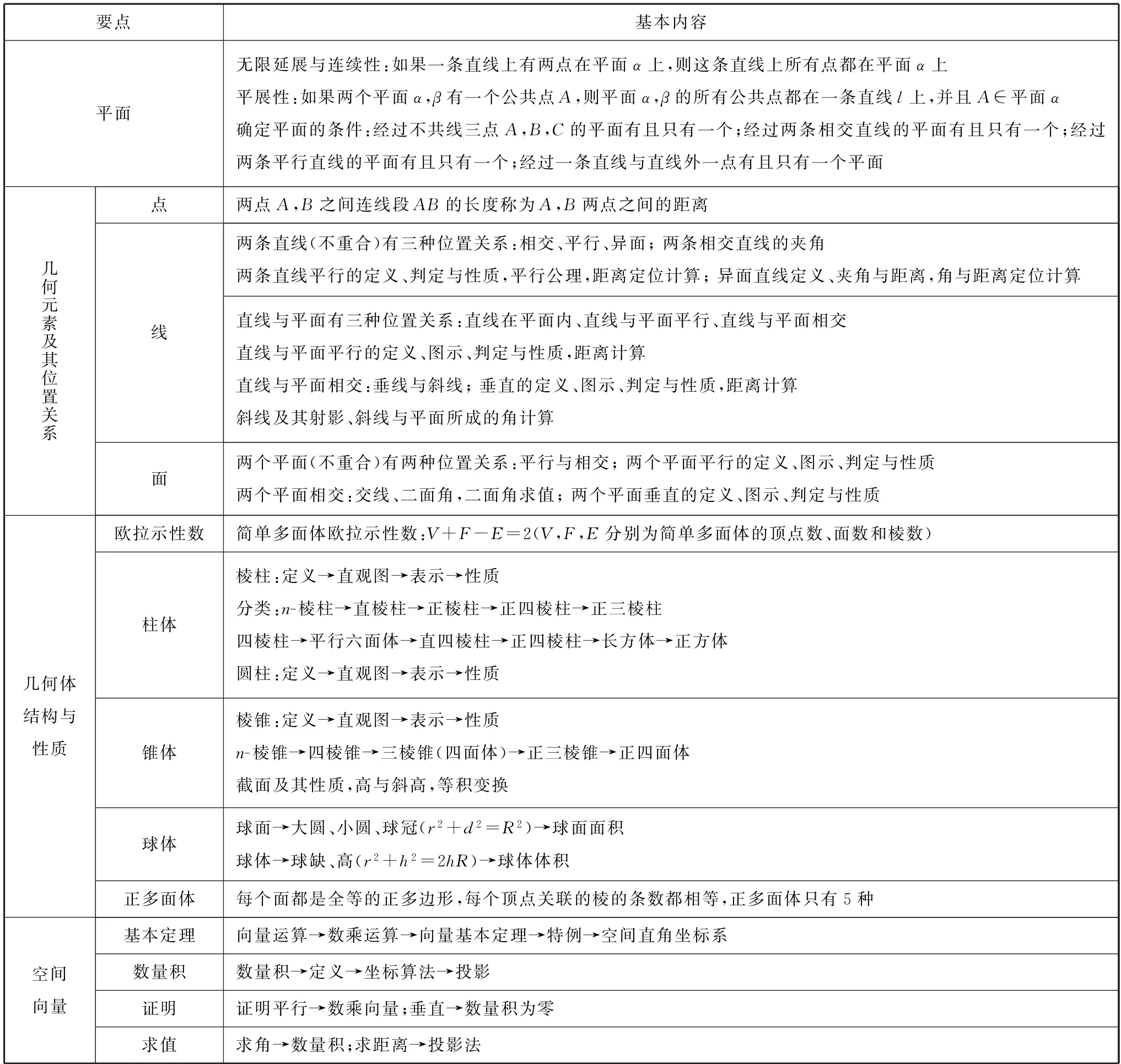
表1
1.2 要点解析
(1)几何观点:基于几何体概念以及相关几何元素之间的位置关系,经历图形分析与必要的几何作图过程,根据定义与性质进行推理,完成证明与计算.
(2)几何作图:基于几何分析,在已有空间图形中,增添必要的几何元素以辅助推理与计算.
(3)如图1所示,特殊三棱锥P-ABC的顶点在底面上的射影位置:当PA=PB=PC时,点P在平面ABC上的射影是△ABC的外心;当∠PAB=∠PAC时,点P在平面ABC上的射影落在∠BAC的平分线上.特别地,当∠PAB=∠PAC,且∠PBA=∠PBC时,点P在平面ABC上的射影是△ABC的内心或旁心;当dP-AB=dP-AC=dP-BC时,点P在平面ABC的射影是△ABC的内心或旁心;当PA⊥BC,且PB⊥AC时,点P在平面ABC上的射影是△ABC的垂心.
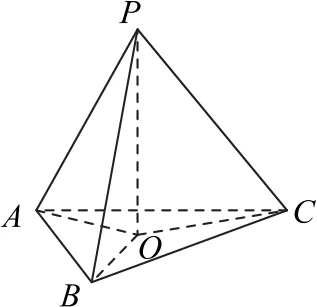
图1
(4)几个常用的二级结论.
三余弦定理:如图2所示,P∉α,PO⊥平面α于点O,点A是平面α内异于点O的一点,∠PAO=θ1,它是PA与平面α所成角,另取点B∈平面α,使得∠OAB=θ2,记∠PAB=θ3,则cosθ1cosθ2=cosθ3.
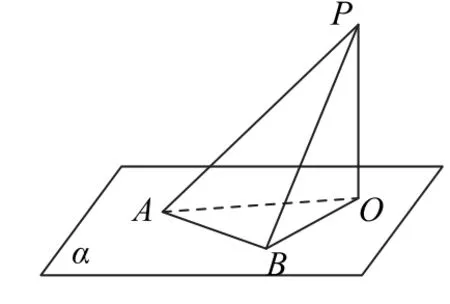
图2
面积射影关系:如图3所示,AA′⊥平面BCA′,二面角A-BC-A′的平面角大小是∠ADA′,设∠ADA′=θ,则S△ABCcosθ=S△A′BC.
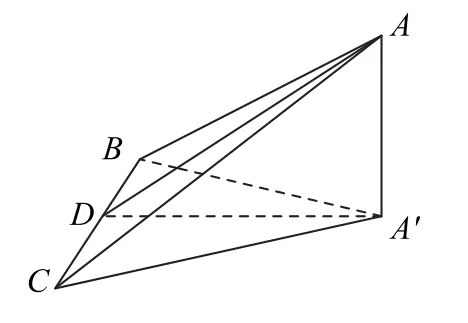
图3
异面直线上两点之间的距离:如图4所示,两条异面直线a,b的距离是d,所成角是θ,A∈a,B∈b,A和B两点的连线段是a,b的公垂线段,E∈a,F∈b,并且AE=m,BF=n.由B和a确定一个平面β,在平面β上过点B作a′∥a,由b和a′确定一个平面α;由AB⊥a,得AB⊥a′,所以平面β⊥平面α;过E作EM⊥平面α于M,则M∈a′.

图4
在△MBF中,BM=AE=m,BF=n,∠FBM∈{θ,180°-θ},下面求FM.

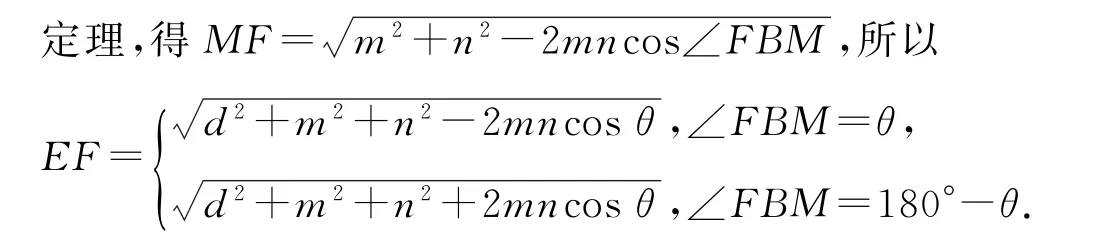
二面角的两个面上两点之间的距离:如图5 所示,在平面α,β内分别取一点M,N,从这两点分别引棱l的垂线段MA,NB,并且MA=m,NB=n,记AB=d,其在平面α上,过点B作线段BT与AM平行且相等,连接MT,则四边形ABTM是矩形,故MT∥l,且MT=d,连接NT,由AB⊥平面BNT,得MT⊥平面BNT.在△NBT中,BN=n,BT=m,∠NBT=θ,由余弦定理得
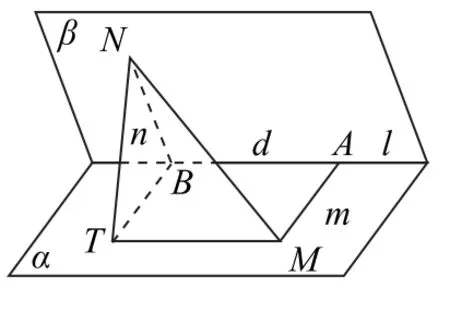
图5
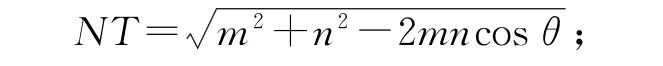
在Rt△TMN中,∠MTN=90°,MT=d,由勾股定理可得

(5)锥体截面与高比例关系:平行于棱锥底面的截面,其面积与底面面积的比等于从顶点到截面的距离与从顶点到底面的距离比的平方.如图6所示,在五棱锥P-ABCDE中,五边形A′B′C′D′E′是平行于底面的一个截面,PO⊥平面ABCDE交平面A′B′C′D′E′于 点O′,则.同理,如图7所示,在圆锥PO中,R分别为圆O′、圆O的半径).
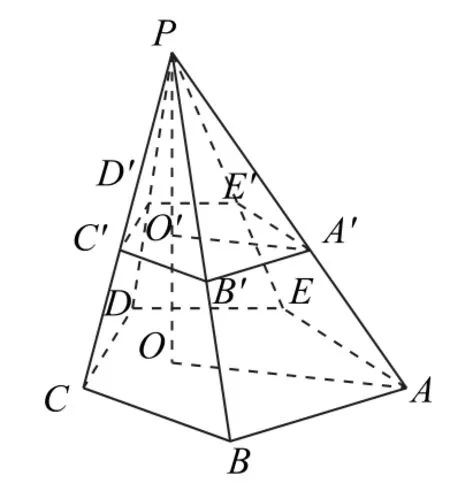
图6
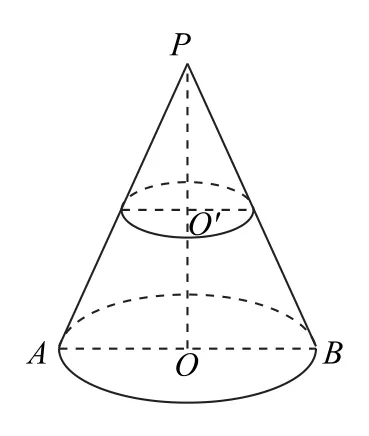
图7

(6)四面体有外接球与内切球.
任意一四面体ABCD都有外接球和内切球.
证明如图8所示,记△BCD的外心为O,过点O作平面BCD的垂线l,任取O′∈l,则O′B=O′C=O′D.取点O′=O1,使O1B=O1C=O1D<O1A;取点O′=O2,使O2B=O2C=O2D>O2A.
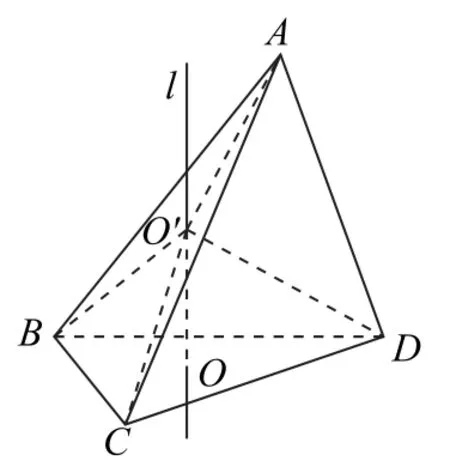
图8
因为当点O′在直线l上连续移动时,差值δ=O′D-O′A连续变换,由介值定理,在线段O1O2上存在一点O,满足δ=0,即OB=OC=OD=OA,则点O为四面体A-BCD的外接球球心,故任意一四面体都有外接球.如图9所示,作二面角A-BC-D的等分角面BCE,再作二面角A-BD-C的等分角面BDF,记BE∩DF=K,则平面BCE∩平面BDF=BK.

图9
作二面角A-CD-B的等分角面CDG,连接AK并延长交CD于点X,则平面AXB∩平面CDG=XG,所以XG与BK是平面ABX上的两条相交直线,记XG∩BK=O,则点O是上述三个等分角面的公共点,所以点O到平面ABC、平面ACD、平面ABD等距离,点O是四面体A-BCD内切球的球心,故任一四面体总有内切球.
(7)等积变换.
祖暅原理:夹在两个平行平面之间的几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面面积都相等,则这两个几何体的体积相等.
三棱锥A-BCD是等积变换最活跃的几何体,即
(8)简单多面体的欧拉示性数:V+F-E=2(多面体的顶点数为V,面数为F,棱数为E).记V+FE=f,现用图论方法论证这个示性数公式f=2.
设想多面体的面是用橡皮做成,先剪掉一个面,再把剩余部分展开,得到一个平面图G(V,E),其中区域数为F-1,数值f-1=V+F′-E不变;再从外向里逐步去掉边(该边关联的2个顶点不去掉),每去掉一条边,面也同时减少一个,数值f-1=V+(F′-1)-(E-1)=V+F′-E保持不变,直到不存在由边围成的区域,这时图G(V,E)简化成树,f-1的值仍保持不变;再从树枝末端,逐步去掉一个顶点及其关联的边,每次操作,顶点与边各减少1,因此f-1=V+F′-E的值不变;这种操作可以直至剩下一条边及其关联的两个顶点,所以f-1=2+0-1=1,即f=2,则V+F-E=2.
(9)正多面体.
五种正多面体:每个正多面体的顶点数记作V、面的个数记作F、棱的条数记作E.

综上,共有五种正多面体,如表2所示.

表2


图10
求平面的斜线l与平面α的夹角归结为直线l与其在平面α上的射影的夹角,即两条相交直线的夹角,这时更常用的方法是通过直线l的方向向量a与平面α的法向量n的夹角进行转化,但〈a,n〉∈(0,π),所以
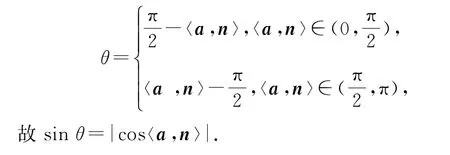
求二面角α-l-β的平面角θ∈(0,π),分别求出平面α,β的法向量n1,n2,这两个法向量夹角〈n1,n2〉的取值范围是(0,π),所以当n1,n2都指向二面角内部或都指向n1,n2外部时,θ=π-〈n1,n2〉;当n1,n2之一指向二面角内部,另一个指向二面角外部时,θ=〈n1,n2〉,故|cosθ|=|cos〈n1,n2〉|,因此sinθ=.应注意的是cosθ=±cos〈n1,n2〉都会出现,正负选择依据是识别两个法向量的方向.
(12)各种距离形式不变性:如图11所示,点到直线的距离、点到平面的距离、两条平行线间的距离、两条异面直线间的距离、线面平行线与平面之间的距离、两个平行平面间的距离,都可以归结为一个向量在另一个向量n(法向量)上的投影的绝对值,即,其中S是l或平面α,n是S的法向量.
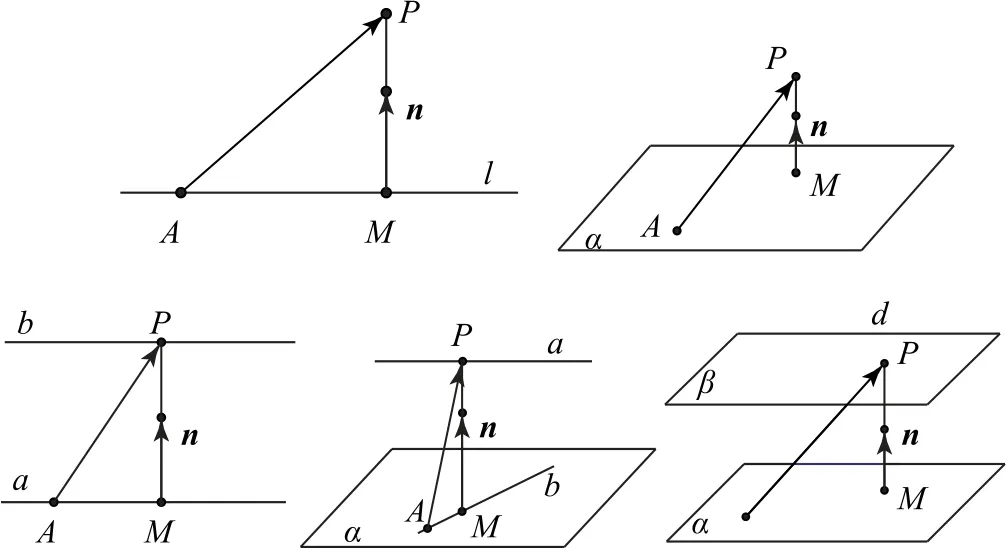
图11
(13)空间四边形对边垂直的条件:如图12 所示,三棱锥A-BCD对棱垂直的条件是
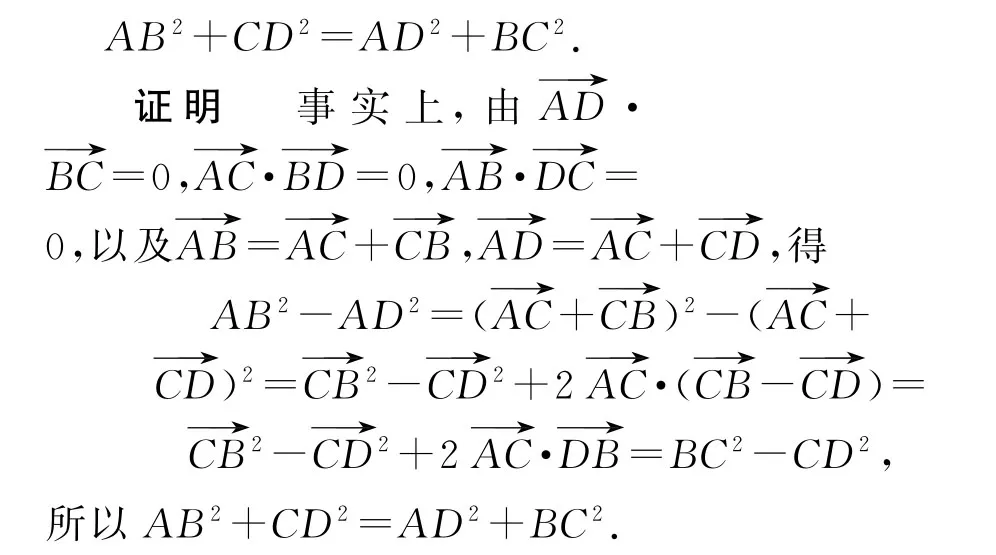
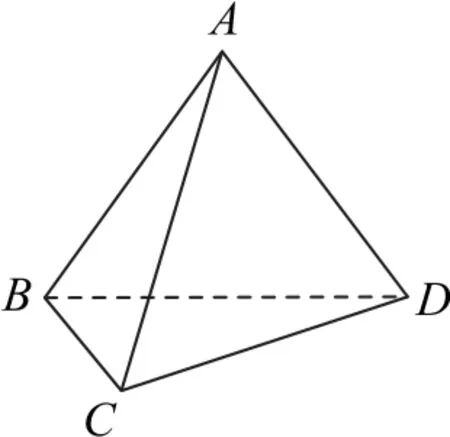
图12
注:体会本结论与下文例4的区别.
2 典例精析
2.1 几何分析
1)动态判断
例1(上海交通大学)如果三条直线a,b,c两两异面,那么与这三条直线都相交的直线l是否存在? 若存在,是有限条还是无穷多条?
解析这样的直线l存在,并且有无穷多条.把两两异面的三条直线a,b,c置于一个平行六面体的三条棱上,如图13 所示,直线BC、直线C′D′、直线AA′分别是直线a,b,c.在直线BC上任取一点X∉{B,C},由X∉c,知经过点X与直线c有唯一一个平面α,记b∩平面α=Y,由c⊆平面α,XY⊆平面α,并且c与XY不平行,可知c∩XY=Z,记共线三点X,Y,Z所在直线为lX,则lX∩a=X,lX∩b=Y,lX∩c=Z,所以存在满足题设条件的直线lX,并且点X在直线a上移动时,直线lX也是变化的,故满足题设条件的直线有无穷多条.
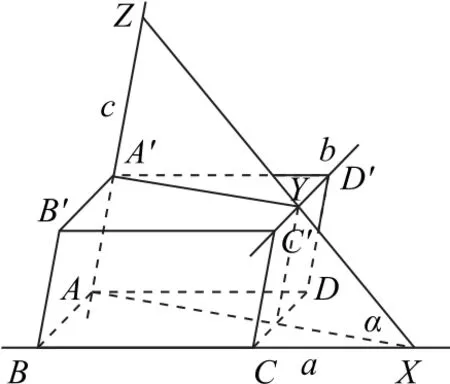
图13
2)异面直线夹角与距离
寻求几何图形中平行线,做平行移动,对所求角与距离进行定位,再进行几何计算.
例2正方体ABCD-A′B′C′D′的棱长为1(如图14-甲),求两条异面直线B′D′与BC′所成角与距离.
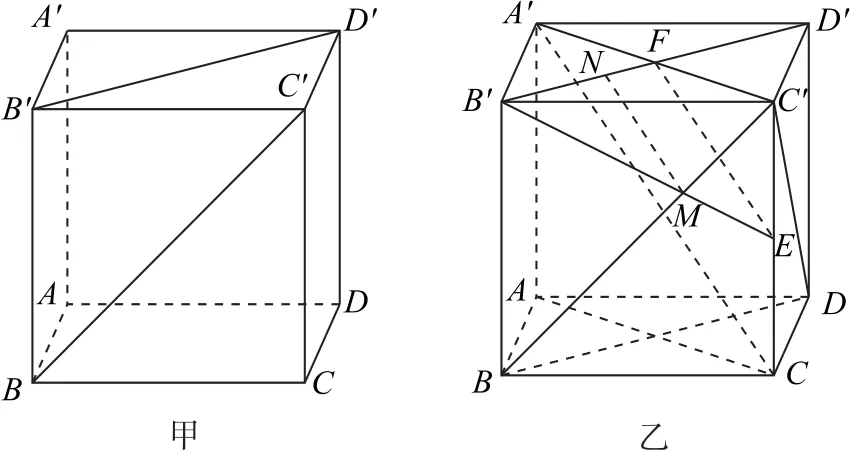
图14
解析如图14-乙所示,由于B′D′∥BD,故∠C′BD就是两条异面直线B′D′与BC′所成角,连接C′D,则BC′=C′D=BD=,所以△C′BD是一个正三角形,从而∠C′BD=60°,故两条异面直线B′D′与BC′所成角为60°.
因为B′D′⊥A′C,B′D′⊥CC′,所以B′D′⊥平面A′CC′,从而A′C⊥B′D′.同理,A′C⊥BC′,故A′C与两条异面直线B′D′,BC′都垂直.下面由A′C追寻这两条异面直线的公垂线.
记A′C′∩B′D′=F,取棱CC′的中点E,则EF是△C′A′C的中位线,即EF∥A′C,并且
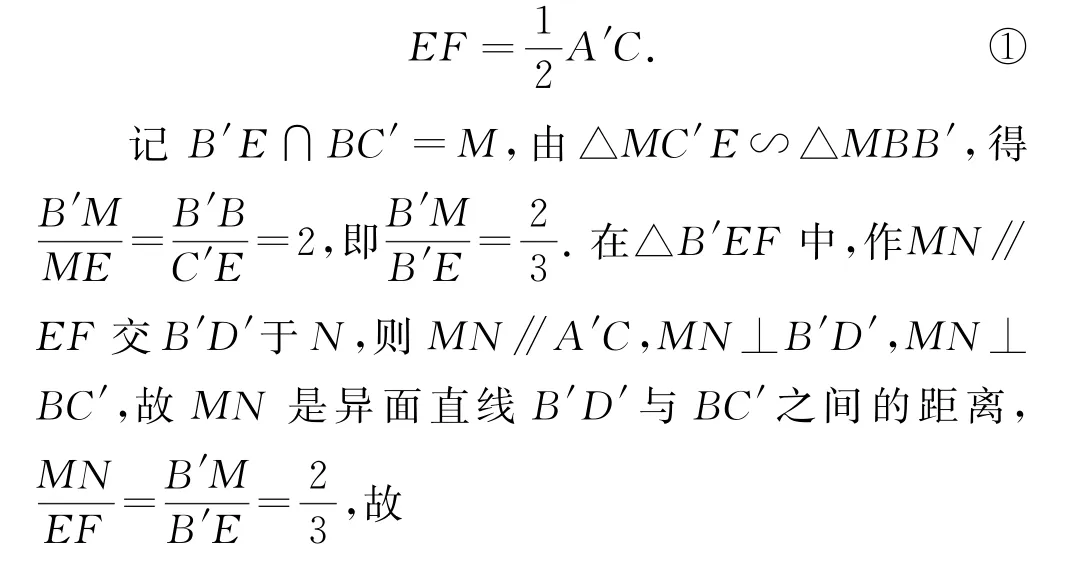

3)论证平行与垂直
平行与垂直是立体几何推理论证的主要问题,证明的基本路径是基于题设几何元素位置关系,运用相关定理(判定与性质)以逻辑推理构建完整通顺、自然流畅的证明过程.
例3三个平面α,β,γ两两相交,记α∩β=l1,β∩γ=l2,γ∩α=l3,求证:
(1)如图15-甲所示,若l1∥l2,则l1∥l3;
(2)如图15-乙所示,若l1∩l2=P,则P∈l3.

图15
证明(1)因为l1∥l2,l1⊄γ,l2⊂γ,所以l1∥γ.因为l1⊂α,α∩γ=l3,所以l1∥l3.
(2)因为l1∩l2=P,l1⊂α,l2⊂γ,所以P∈α,且P∈γ.因为α∩γ=l3,所以P∈l3.
例4在三棱锥A-BCD中,AB⊥CD,AC⊥BD,求证:该三棱锥的每个顶点在其对面上的射影都是相应面三角形的垂心.
证明三棱锥中有两组对棱垂直,证明三个顶点在其对面上的射影都是垂心,只需证明顶点A在平面BCD上的射影是△BCD的垂心H.如图16所示,作AH⊥平面BCD于H,则CD⊥AH,BD⊥AH.
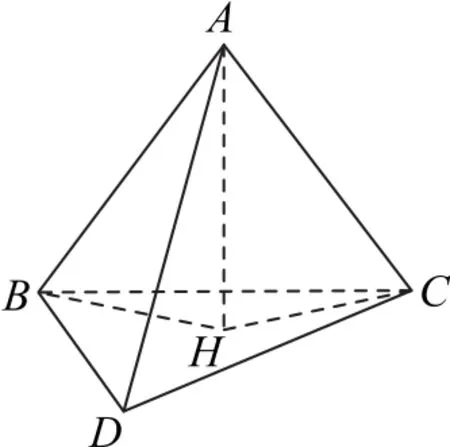
图16
因为CD⊥AB,BD⊥AC,所以CD⊥平面ABH,BD⊥平面ACH,故CD⊥BH,BD⊥CH,从而H是△BCD的垂心.
点评把两者结合起来可知,当四面体有两组对棱互相垂直时,第三组对棱也互相垂直,这时三组对棱的平方和相等,并且每个顶点在对面上的射影都是相应三角形的垂心.
4)体积计算与变换
除求空间角与距离之外,求体积是几何计算的另一典型内容.基于目标与体积公式,作几何计算,探求中间数据,指向求体积.另外,基于三棱锥或四面体进行等积变换,也是简化几何计算的有效路径,尤其是不用作出表示距离的垂线段.
例5 若四棱锥P-ABCD的棱AB,BC的长均为,其他各条棱长均为1,求该四棱锥的体积.
解析如图17 所示,作PO⊥平面ABCD于点O.由PA=PB=PC=PD=1,所以OA=OB=OC=OD,故A,B,C,D四点共圆,O是外心.
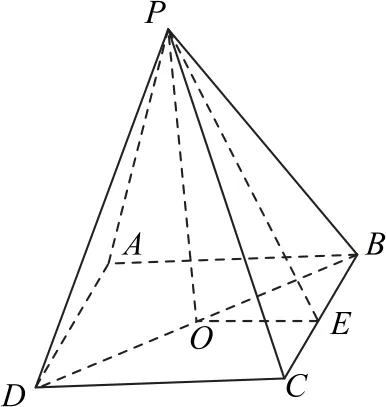
图17
由题意,BA=BC=,PA=PC=1,所以△PBA≌△PBC⇒∠PBA=∠PBC⇒BO平 分∠ABC;同理DO平分∠ADC.
由题意,△ABD≌△CBD⇒BD平分∠ABC与∠ADC,故点O在BD上,O是线段BD的中点,BD是四边形ABCD外接圆的直径,从而∠BAD=90°=∠BCD.

例6 如图18所示,过正三棱锥D-ABC底面正△ABC的中心O任意作一平面α,记射线DA,DB,DC分别与平面α相交于点P,M,N.记AD=l,求证是常数.
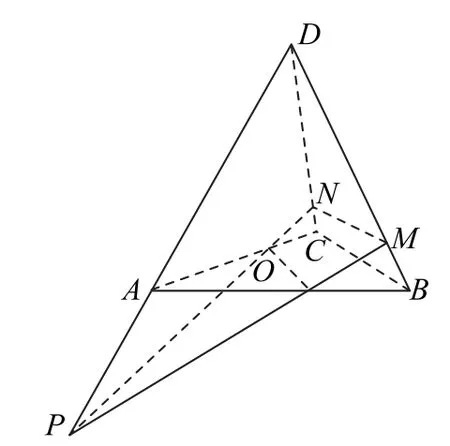
图18
解析如图19所示,连接OP,OM,ON,把动态四面体D-MNP分割成3个四面体O-DMP,O-DMN,O-DNP.记∠ADB=∠BDC=∠CDA=θ,DO=h,DO与平面DAB,平面DBC,平面DCA成等角α,每条侧棱DA,DB,DC与其相对侧面成等角β.
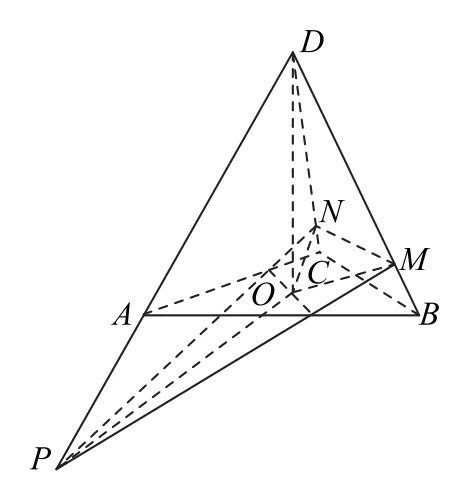
图19

5)铺平与翻折
基于平面图形翻折立意的一类立体几何问题,要分析翻折过程中某些垂直与平行的不变性,作为推理基础,同时要注意后续空间计算的中间数据也能回到原平面图形,从而快捷合理地探求.另一方面,铺平方法也是计算空间最短距离问题的一条快捷路径.
例7(上海交通大学)如图20所示,已知矩形ABCD的边AB=,过B,D作AC的垂线,垂足分别为E,F,并且E,F恰是线段AC的三等分点,沿着AC将矩形翻折,使得二面角B-AC-D是直二面角,则BD的长度为__________.
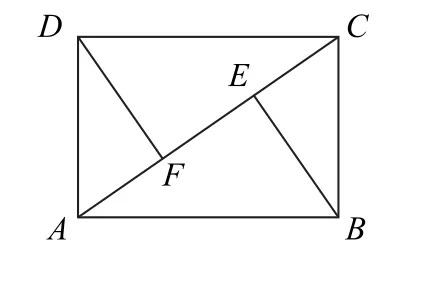
图20

图21
解析如图21所示,作出折叠图形的直观图,得到三棱锥D-ABC.由题意以及折叠过程中的不变性,可知平面DAC⊥平面ABC,且DF⊥AC,则DF⊥平面ABC,即∠DFB=90°,所以

点评求解折叠问题应按动态情境体验图形折叠前后不变性质与折叠以后空间图形的形状,这是正确推理与计算的基础.本例也可以用如下方法求解简化计算.记AF=EF=EC=m,则
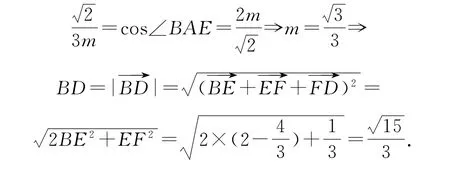
例8(北京大学)设P为单位正方体ABCDA1B1C1D1的面对角线AB1上的动点,则PA1+PC1的最小值是_________.
解析如图22 所示,因为点P在定线段AB1上移动,所以PC1始终在平面AB1C1D上,故把平面AA1B1绕AB1逆时针旋转铺平到平面AB1C1D上,得到平面图形AHB1C1D,记AB1∩HC1=P0,当P=P0时,(PA1+PC1)min=P0H+P0C1=HC1,这里的HC1是平面图形AHB1C1D上的线段.
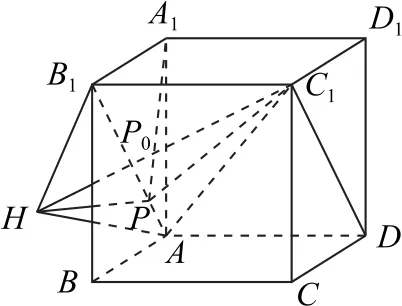
图22
2.2 向量法
应用向量加、减法、平行四边形法则、三角形法则以及基本定理建立目标,经向量运算与数量积进行推理,完成几何证明与计算.
例9题目同例6.

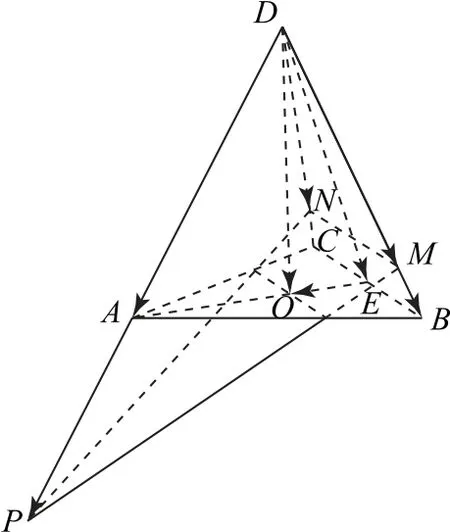
图23

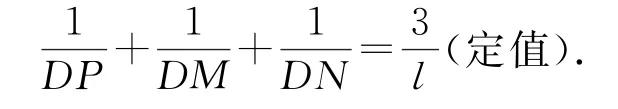
2.3 坐标法
传统几何法求空间角与距离都得作出相应的几何图形,再基于图形性质进行几何计算,这对几何作图能力要求较高.基于现在的学情,学习坐标法既是对几何法的补充也是深化,形成代数几何新思维.以坐标法构建几何推理与探求几何计算的基本路径:基于图形结构特点,合理建立空间直角坐标系,把已知数据坐标化,写出相关点的坐标,进而写出或求出有关向量的坐标,经向量运算或数量积、投影计算,完成几何推理与计算.学生通过解题应该体验到适当引入几何推理可以简化代数计算.因此,要善于在坐标计算过程中进行几何分析与推理,合理简化计算.
例10在三棱锥P-ABC中,∠APB=∠APC=60°,∠BPC=90°,PA=3,PB=2,PC=1,则该三棱锥P-ABC的外接球半径为R=________.
解析如图24 所示,以P为原点,射线PB为x轴正方向,射线PC为y轴正方向,建立空间直角坐标系P-xyz.取线段BC的中点D,则D是Rt△PBC的外心,三棱锥P-ABC的外接球球心O在过点D与平面PBC垂直的直线上,记其外接球半径为R.
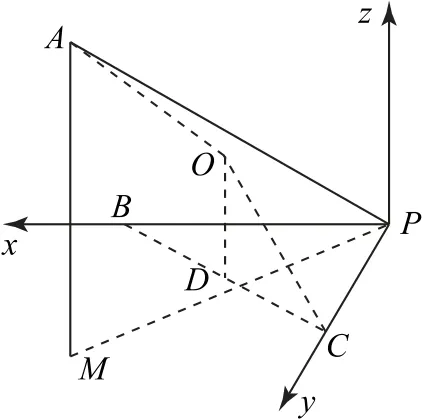
图24

3 实战演练
1.(山东大学)如图25所示,在空间直角坐标系O-xyz中,三角形ABC在三个平面的投影面积分别为3,4,5,则该三角形的面积为________.
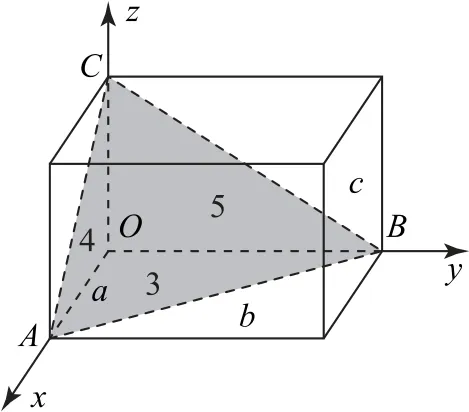
图25
2.(中国科学技术大学)如图26 所示,等边△ABC的边长为1,D,E分别在边AB,AC上运动,并且DE∥BC,将ADE沿DE折叠,得到四棱锥A-BCDE,求其体积V的最大值.
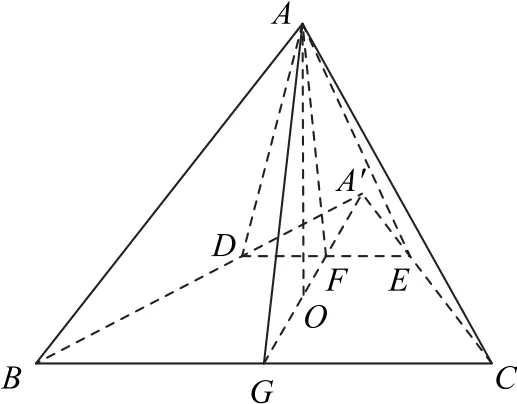
图26
3.(中国科学技术大学)设空间区域W={(x,y,z)|x2+y2+z2≤1,z≥0}中存在四个点两两距离都是d,则dmax=________.
4.(武汉大学)空间图形W={(x,y,z)|0≤x≤y≤z≤1}的体积为( ).
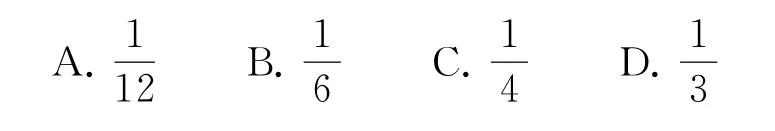
5.(上海交通大学)用一个平面截一个单位正方体,若截面是与体对角线垂直的六边形,则此六边形的周长为________.
6.(上海交通大学)若四面体的各个顶点到平面α的距离都相等,则称平面α为该四面体的中位面,则一个四面体的中位面的个数为_________.
7.一个正四面体与一个正四棱锥的所有棱长都相等,现把这两个几何体以一个侧面对接起来,得到的多面体是________面体.
(完)
