点动成线,点动带面,点动构体
——空间中的动态问题
2023-01-07王飞
王 飞
(北京师范大学遵义附属学校)
空间立体几何中的动态问题是创新情境背景下的一类特殊问题,主要是通过空间动点的运动变化,结合一些特殊条件的限制,由此形成点动成线,点动带面,点动构体,从而形成与轨迹、长度、角度、面积、体积等要素相关的问题.破解此类问题的关键是合理审题,抓住运动过程中一些“动”的要素与“不动”的要素,认真分析其变化特点,寻找不变的静态因素与改变的动态因素之间的关系,从静态因素中,寻找解决问题的突破口.
1 点动成线
点动成线问题,往往是由动点在空间几何体的表面运动时所形成的轨迹长度或截面的周长等问题,结合动点的运动规律,准确地确定动点的轨迹或截面的几何图形是解决此类问题的关键.
例1已知正方体ABCD-A1B1C1D1的棱长为2,M为棱C1D1的中点,点N在正方体的表面上运动(N不与B1重合),且B1N⊥AM,则动点N的轨迹长度为( ).
解析如图1所示,连接BC1,A1M,则AM在平面A1B1C1D1和平面BCC1B1上的投影分别为A1M,BC1.
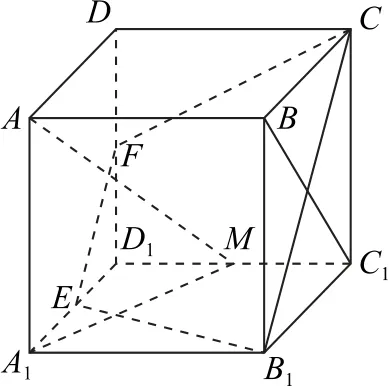
图1
分别取A1D1,DD1的中点E,F,连接B1E,EF,FC,CB1,因为E是A1D1的中点,F是DD1的中点,所以EF∥B1C,又EB1=FC,所以四边形B1EFC是等腰梯形.
因为E是A1D1的中点,M为C1D1的中点,底面A1B1C1D1是正方形,所以B1E⊥A1M,B1E⊥AA1,AA1∩A1M=A1,所以B1E⊥平面AA1M,而AM⊂平面AA1M,所以AM⊥B1E.
因为BC1⊥B1C,所以AM⊥B1C,又因为B1E∩B1C=B1,所以AM⊥平面B1EFC,而点N在正方体的表面上运动,且B1N⊥AM,故动点N的轨迹为等腰梯形B1EFC的边界.

点评解决此类点动成线问题,关键就是确定动点的轨迹或截面的几何图形,利用空间图形的特征以及限制条件,将“三维”空间降维转化到“二维”平面上,在“二维”平面上寻觅动点的轨迹或截面的几何图形等,为破解问题奠定基础.
2 点动带面
点动带面问题,往往是由动点在空间几何体的线段或平面上运动时所确定的满足条件的截面问题,往往同直线与平面垂直、平行有关,准确地确定与动点有关联的截面是解决此类问题的关键.
例2在棱长为1的正方体ABCD-A1B1C1D1中,P是线段BC1上的点(包括端点),过点A1的平面α与直线PD垂直.当点P在线段BC1上运动时,平面α截正方体ABCD-A1B1C1D1所得的截面面积的最小值是( ).
解析如图2 所示,当点P在点B处时,连接A1C1,AC,易知BD⊥平面ACC1A1,平 面ACC1A1即为平面α,则平面α截正方体ABCDA1B1C1D1所得的截面面积为,此时截面的面积最大.
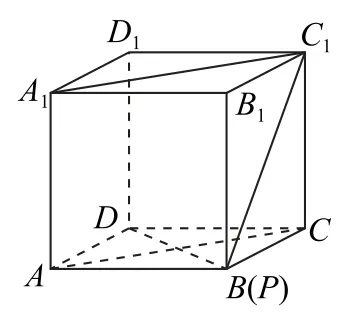
图2
如图3所示,当点P与点C1重合时,连接A1B,D1C,DC1⊥平面A1D1CB,平面A1D1CB即为平面α,则平面α截正方体ABCD-A1B1C1D1所得的截面面积为,此时截面的面积最大.

图3
当点P由点B向点C1运动时,设平面α与C1D1的交点为F,与AB的交点为E,连接A1F,FC,CE,EA1,EF,A1C,平面α截正方体ABCDA1B1C1D1所得的截面为四边形A1ECF.

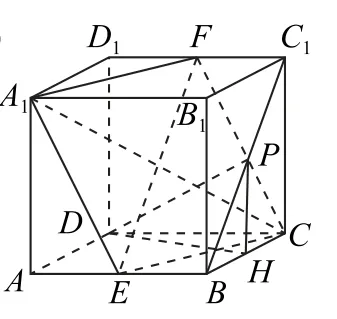
图4
综上,平面α截正方体ABCD-A1B1C1D1所得截面面积的最小值是,故选C.
点评解决此类“点动带面”问题,关键是确定与动点有关联的截面的位置关系、形状等相关问题,利用直线与平面垂直、平行等相关的定理、性质加以分析与推理,由此确定满足条件的截面,为问题的求解提供条件.
3 点动构体
点动构体问题,往往是由动点在空间几何体的线段或表面上运动时所确定的直线、截面与其他固定要素所组成的问题,延伸出空间几何体的表面积、体积以及角度等相关问题,准确地确定满足条件的空间几何体是解决此类问题的关键.
例3已知正三棱柱ABC-A1B1C1的体积为,D是B1C1的中点,点P是线段A1D上的动点,过BC且与AP垂直的平面α与AP交于点E,则三棱锥P-BCE的体积的最小值为( ).


图5
点评解决此类点动构体问题,关键是确定与动点有关的空间几何体的形状与特征,利用空间几何体的定义、性质、公式等进行推理,确定与之对应的空间几何体,为问题的进一步求解指明方向.
空间立体几何中的动点问题常常隐藏动点所处的几何模型,解决问题的关键是抓住动点的运动规律,挖掘出几何模型.同时在解决问题过程中,要善于发挥空间想象能力以及逻辑推理能力,做到“胸有图形”,“动”中寻“宝”,借助逻辑推理进行定性分析,或引入变化参数进行数学运算,实现“动”与“静”的和谐统一与完善转化.
(完)
