煤颗粒流化床增压富氧燃烧脱挥发分模型

2023-01-07段伦博武万强

煤炭学报 2022年11期

李林，段伦博，武万强，孙光

(东南大学能源热转换及其过程测控教育部重点实验室，江苏南京 210096)

2020-09-22，国家主席习近平在第75届联合国大会一般性辩论上提出了中国将提高国家自主贡献力度，二氧化碳排放力争于2030年前达到峰值，努力争取2060年前实现碳中和。从CO2来源解析，我国CO2的排放主要来源于建筑、工业、交通、电力、炼油、农业等行业，其中有约一半来源于能源行业，而能源行业中煤炭资源消耗带来的CO2排放占比约96%，其中约一半的煤炭资源用于燃煤发电[1]。

CCS技术被认为是未来大规模降低燃煤电站CO2排放最为有效的方法之一[2-3]。其中，富氧燃烧技术被认为是最具发展前景的燃煤电站CO2捕集技术之一。而目前限制富氧燃烧技术商业化的瓶颈仍是较高的能耗。增压富氧燃烧技术是解决这一问题的方法之一。与传统富氧燃烧相比，增压富氧燃烧技术中全流程均置于高压下运行，这样可以带来众多优势：① 降低系统中压力波动带来的功损；② 降低锅炉设备尺寸；③ 可以回收烟气中的蒸汽潜热；④ 避免了系统漏风从而降低纯化压缩系统的功耗等。

近年来，国内外学者针对增压富氧燃烧技术的研究也逐渐引起了学术界和产业界的关注。意大利IETA公司、波兰煤化工过程研究所、渥太华大学及国内的华北电力大学、华中科技大学、东南大学和西安交通大学等多家机构报道过相关研究，这些研究包括增压富氧燃烧系统建模和优化研究[4-6]、燃烧特性[7-9]、污染物排放特性[10-13]以及流动特性[14-15]等方面。但现有对燃烧特性的研究多借助增压热重或者增压管式炉等设备开展，而对真实燃烧条件下煤颗粒增压富氧燃烧机理研究还不充分。

煤颗粒的干燥和脱挥发分过程是燃烧的重要过程。目前，针对煤和生物质等燃料颗粒在流化床条件下的热解模型研究已经较多，但是这些模型研究大多集中在常压条件下，而针对增压富氧燃烧条件下开展热解模型研究的报道还比较少。CHERN和HAYHURST[16-17]通过在流化床内模型研究发现，挥发分燃烧火焰会将热量传递至颗粒表面并提高颗粒的升温速率，SADHUKHAN等[18]的研究也得到了相似的结论。而YANG和WANG[19]通过研究脱挥发分过程中颗粒温度变化特性，发现挥发分燃烧热大多被颗粒周围气流携带走，对颗粒升温的影响有限。BU等[20]认为颗粒热解过程中颗粒一半置于密相区一半置于稀相区，并假设挥发分火焰在稀相区部分均匀包裹于颗粒表面，计算结果发现挥发分火焰对颗粒的平均加热份额较低，可以被忽略。而根据课题组前期研究发现，煤颗粒在密相区热解时大多处于乳化相中，而挥发分会穿过床层后形成火焰，颗粒与火焰完全脱离[21-22]。

为研究增压流态化下的O2/CO2和O2/N2气氛对煤颗粒脱挥发分的影响机制，笔者将建立适用于流态化的颗粒尺度的增压热解模型。并解析高压、高CO2气氛及多种操作参数对煤颗粒脱挥份的影响机制。

1 模型介绍

1.1 模型描述

本工作通过一维非稳态模型描述煤颗粒脱挥发分过程，模型考虑了颗粒与环境之间的传热、颗粒内部的温度梯度、水分蒸发过程和挥发分的析出过程。其中颗粒边界和其外界环境通过边界方程对接。由于流化床燃料颗粒尺寸较大，颗粒内部温度梯度不可忽略。本模型计算过程中，将颗粒沿半径方向等分成n环形球壳，保证每个计算区域内颗粒毕渥数(Bi)远小于0.1，并认为每个网格内颗粒温度是均匀的。当颗粒中心的温度第1次超过373 K时认为颗粒干燥过程结束，而当颗粒中心温度达到床层温度时认为煤颗粒脱挥发分过程结束。计算采用的煤种为小龙潭褐煤(LC)，工业分析和元素分析见表1。

表1 工业分析及元素分析

1.1.1 模型假设

为便于模型的建立和分析，假设：

(1)颗粒始终处于乳化相中，且床层各处温度均匀，颗粒在床层内部换热特性不受位置影响;

(2)煤颗粒为均匀的球形颗粒，不同网格内其化学组分一致，物性参数(比热容、密度、热导率等)一致；

(3)颗粒在整个干燥和挥发分析出过程中不发生膨胀和破碎等物理变化，颗粒尺寸始终保持恒定；

(4)颗粒干燥过程中，水分蒸发的温度为373 K；

(5)脱挥发分反应过程中，认为反应的活化能和指前因子等动力学参数不随压力变化；

(6)挥发分析出和燃烧的过程是不可逆的准稳态过程，挥发分在床层上部燃烧并形成的火焰对煤颗粒的加热过程没有影响。

1.1.2 控制方程

煤颗粒干燥和挥发分析出的过程中，沿着颗粒半径方向不同计算网格内的密度和温度均会发生变化，颗粒密度和温度的变化可以描述为

Vp∂ρp/∂t=-s1

(1)

(2)

式中，ρp，Vp，cp，Tp和R分别为煤颗粒的密度(kg/m3)、体积(m3)、比热容(J/(kg·K))、温度(K)和半径(m)；λp为煤颗粒导热系数，W/(m·K)；s1和s2分别为因水分蒸发过程和挥发分析出过程引起的煤颗粒质量和温度的变化。

初始条件下(t=0)，ρp=ρp,0，当0≤r≤R时，Tp=Tp,0。颗粒边界条件为

∂Tp/∂r=0(t>0，r=0)

(3)

λp∂Tp/∂r=htotal(Tb-Tp)(t>0，r=R)

(4)

其中，Tb为床层温度，K；htotal为床层与颗粒之间的换热系数。不同温度条件下颗粒的热导率、密度和比热容等参数的计算过程可见文献[23]。

1.2 反应模型

将煤颗粒在干燥过程中温度达到373 K的界面定义为蒸发界面。随着干燥过程推进，蒸发界面半径(ref)缩小，蒸发界面(r=ref)处的水分蒸发速率(kdry)为

(5)

本模型中煤颗粒的脱挥发分过程采用无穷平行反应模型描述，脱挥发分过程中某一反应i的反应速率常数(ki)由Arrhenius方程描述，脱挥发分反应速率为

(6)

(7)

其中，V为某一时间下挥发分析出量， kg/kg；V*为颗粒中挥发分，kg/kg；k0为速率常数；Rg为摩尔气体常数，J/(mol·K)；E，T分别为活化能(J/mol)和温度(K)。当时刻为t时，煤颗粒挥发分析出总量为各个平行反应的累计析出量，可用式(6)描述为

(8)

式中，Apyro为热解反应的指前因子，1/s；f(Epyro)为热解反应活化能Epyro的高斯分布函数。

1.3 换热模型

本模型中颗粒与环境间的换热系数[24]可描述为

htotal=hconv+hcond+hradi

(9)

式中，hconv，hcond和hradi分别为床层与颗粒之间的对流换热系数、导热换热系数和辐射换热系数(W/(m2·K))，详细计算过程可以参考文献[24-27]。

1.4 模型求解策略

将颗粒沿半径方向均匀的划分为M个单元体，厚度为R/M，模拟过程中对每个单元体的控制方程采用有限体积法进行求解。首先对M和计算的时间步长(Δt)进行无关性验证。不同的M下各个单元体Bi分布情况如图1所示。可以发现，从颗粒中心到外表面，单元体Bi逐渐增大，同一M条件下，当M>10时，各个单元体Bi均小于0.1。通常为Bi小于0.1时可以认为单元体温度均匀，忽略温差。对M和Δt的无关性进行分析结果如图2所示。可以发现随着M的增加，模型计算所得煤颗粒干燥时间逐渐下降，但是变化越来越小。而随着Δt的减小，模型计算所得煤颗粒干燥时间逐渐下降。综合分析可得，当M为50，Δt为0.001 s即可获得较好的数值计算精度。

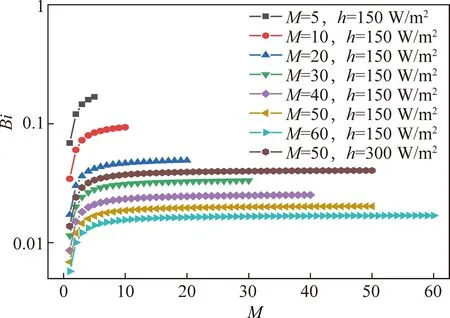
图1 不同M时各个单元体的Bi Fig.1 Distribution of Bi for different values of M

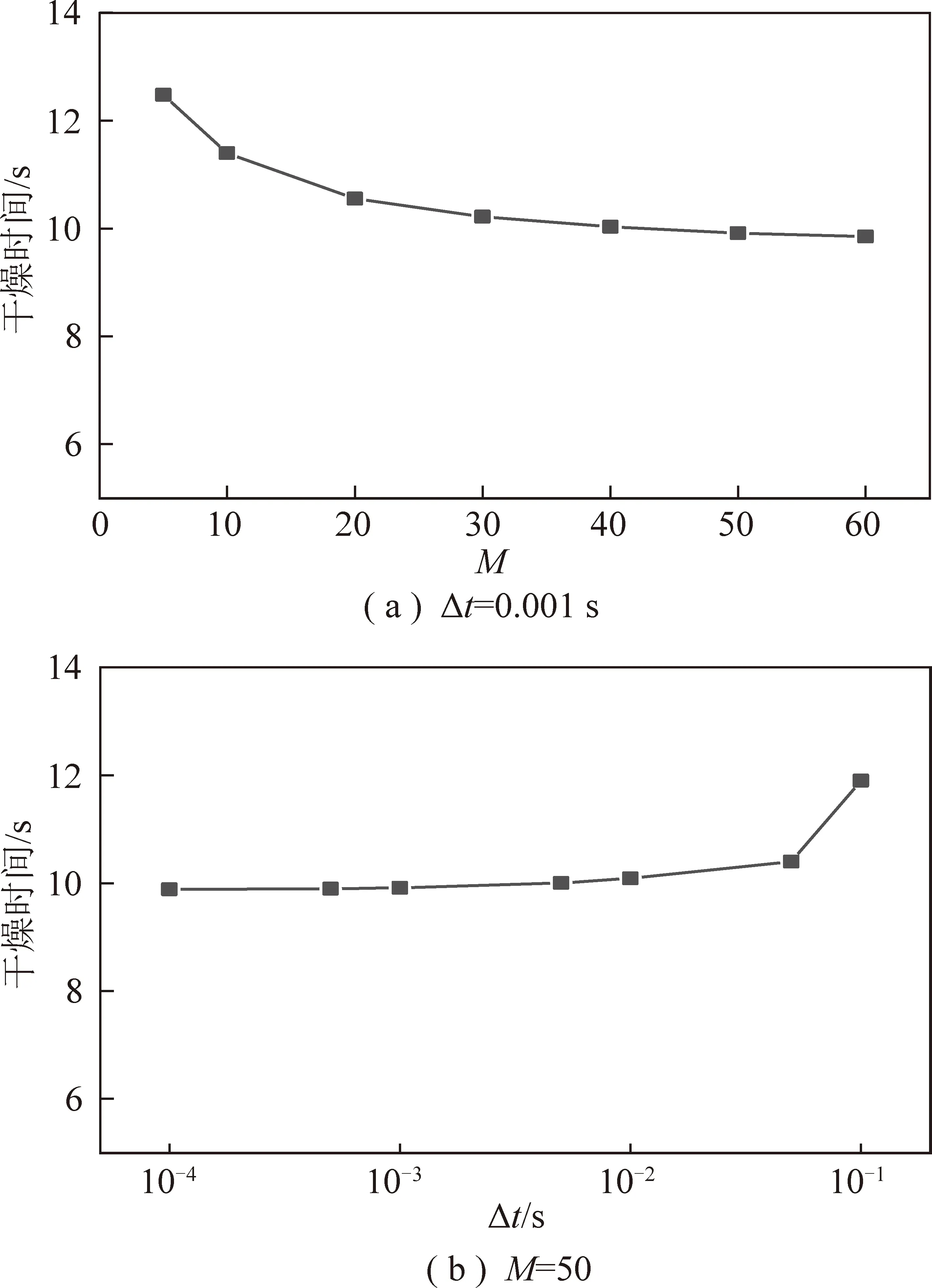
图2 不同Δt和M时煤颗粒的干燥时间变化Fig.2 Variation of drying time with different Δt and M

2 结果与讨论

2.1 模型分析

2.1.1 煤颗粒干燥和脱挥发分过程

煤颗粒在不同压力和气氛下温度变化如图3所示,可以看出，当煤颗粒进入流化床内后，迅速被炽热的床料加热，导致颗粒外表面温度迅速上升。但由于自身相对较小的导热系数，颗粒中心的温度则响应较为缓慢。颗粒不同位置(r=0，1，2，3 mm)的温度变化均经历了相似的温升过程。即颗粒首先升温至373 K进行干燥，这一阶段会出现一个“平台”，直至干燥过程结束。进而颗粒挥发分开始析出，随着挥发分的析出，颗粒温度曲线在600～700 K间会出现“第2个平台”，这主要是由颗粒的热导率、比热容和密度等参数变化引起的。随着颗粒温度的上升，其与环境之间的温差逐渐减小，颗粒升温速率逐渐下降。如图3所示，随着压力的升高，颗粒与环境间换热系数显著增强，一方面降低了颗粒的干燥时间和脱挥发分时间，另一方面会导致颗粒内外温差增大。煤颗粒尺寸为6 mm时，N2和CO2气氛下，当压力从0.1 MPa升高到0.5 MPa时，颗粒内外温差峰值(ΔTmax)分别从309 K和312 K升高到316 K和331 K。

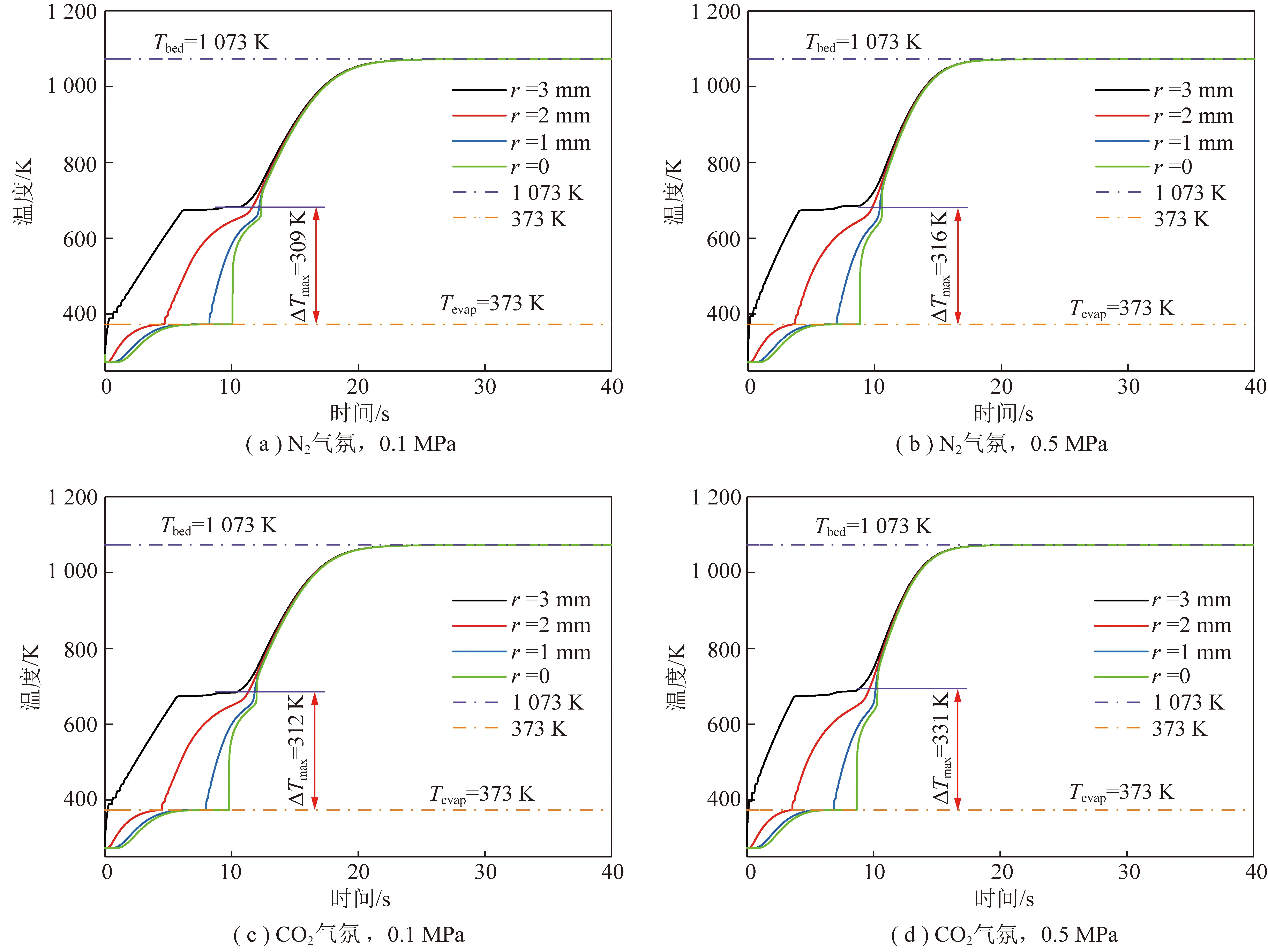
图3 煤颗粒不同位置温度变化曲线(w=2.5,dp=6 mm)Fig.3 Temperature variation curves of coal particle in different positions (w=2.5,dp=6 mm)

2.1.2 模型验证

笔者课题组前期在可视化增压流化床反应器上开展煤颗粒(粒径为6 mm)增压富氧燃烧实验研究[28]，获取了不同压力(0.1～0.5 MPa)和气氛(O2/CO2和O2/N2)下煤颗粒的干燥和脱挥发分时间。此处用这些结果与本模型的模拟结果进行对比来验证模型可靠性，对比结果如图4所示。计算结果与实验结果具有较好的吻合，模型预测值误差在20%以内。

此外，从图4可以发现，模型可以很好地反应压力变化时传热特性的变化，进而预测煤颗粒的干燥和脱挥发分过程。而当压力不变，氧浓度升高的时候，本模型计算结果与实验结果的偏差增大，这是因为本模型没有考虑煤颗粒表面煤焦燃烧对颗粒的加热作用，而这一作用可以促进脱挥发分过程，且氧气体积分数越高，促进作用越显著。

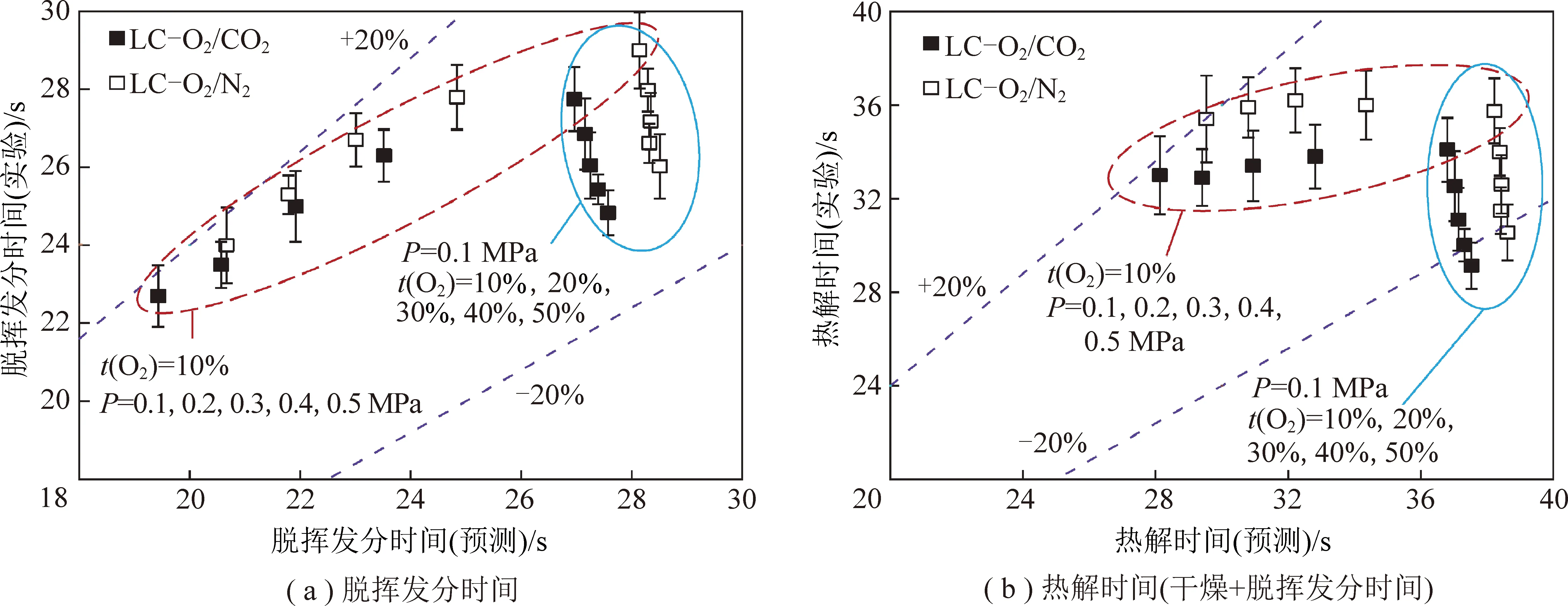
图4 模型预测结果与实验结果的对比Fig.4 Comparison between predicted results and experimental results

2.1.3 模型敏感性分析

在不同的操作条件下，各种参数(例如床料比热容cbed、燃料比热容cfuel、换热系数htotal、燃料挥发分含量Vfuel、燃料水分含量Mfuel、燃料颗粒密度ρp、颗粒尺寸dp以及压力P等)变化会通过改变传热来影响煤颗粒的干燥和脱挥发分过程。通过调整单一参数值(±30%)的方法来研究模型中各参数的敏感性。不同参数的敏感性分析如图5所示。

从图5(a)可以发现，cbed,cfuel,dp,ρp,Mfuel以及htotal对颗粒干燥时间(tdrying)的影响较大，而P和Vfuel对干燥时间的影响较小。燃料颗粒的干燥过程主要受传热过程控制，cbed的提高可以提高床料与颗粒之间的换热系数，从而降低干燥时间。Mfuel,dp以及ρp的增加会增加颗粒含水量，而水分具有较高的气化潜热，因此会带来较高的颗粒干燥时间。如图5(b)所示，干燥和热解时间(tsum)变化主要受cbed，htotal,dp和ρp影响，前2者因素主要影响燃料与床层之间的换热，后2者因素主要影响颗粒中水分和挥发分的总量。图5(c)给出了不同条件对煤颗粒内外温差峰值(ΔTmax)的影响。可以发现，床料cbed,htotal,dp和ρp依然是影响ΔTmax的主要因素。

这些参数的变化对热解过程的影响主要是通过影响换热系数、颗粒导热系数以及颗粒尺寸而产生的。

2.2 不同操作参数对热解过程的影响

2.2.1 压力和气氛的影响

计算的煤颗粒在不同压力和气氛下tdrying和tsum如图6所示，可以发现，相同操作条件下，N2气氛下的干燥时间和脱挥发分时间均大于CO2气氛下，这主要是由于CO2与N2的物性参数(密度、黏度、比热容等)存在差异，这些参数一方面会影响气体与燃料间的对流换热；另一方面还会影响床层的流动状态，进而影响燃料颗粒与床料之间的传递。需要指出的是，2种气氛带来的换热系数差异并不大，当压力为0.1～1.0 MPa内时，2种气氛带来的换热系数的差异均小于10%。因此，相同条件2种气氛下，颗粒的tdrying，tsum以及ΔTmax的差异均小于5%。

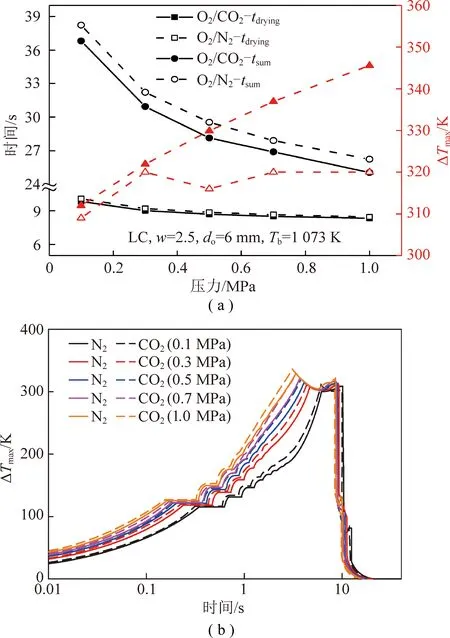
图6 气氛和压力对煤颗粒干燥和脱挥发分过程的影响(dp=6 mm，w=2.5，Tb=1 073 K)Fig.6 Effects of atmospheres and pressure ondrying and devolatilization of coal particle(dp =6 mm,w=2.5,Tb=1 073K)

图6(a)结果还表明随着压力的升高，煤颗粒的tdrying和tsum显著下降，而颗粒内外温差的峰值明显上升。当压力从0.1 MPa升高到1.0 MPa时，2种气氛下tdrying和tsum分别从10.08 s(N2气氛，tdrying)、9.84 s(CO2气氛，tdrying)、38.22 s(N2气氛，tsum)和36.80 s(CO2气氛，tsum)减小到8.46 s(N2气氛，tdrying)、8.33 s(CO2气氛，tdrying)、26.23 s(N2气氛，tsum)和25.03 s(CO2气氛，tsum)，ΔTmax分别从308.91 K(N2气氛)和311.98 K

(CO2气氛)增加到329.75 K(N2气氛)和345.58 K

(CO2气氛)。这是因为压力升高，煤颗粒与床层之间换热系数显著增加，从而缩短了tdrying和tsum。由于煤颗粒尺寸较大，颗粒的Bi大于0.1，因此当换热系数增加时会导致颗粒沿径向温度梯度的增加，颗粒的ΔTmax相应增加。

图6(b)为不同压力和气氛下煤颗粒内外温差变化曲线，可以发现不同压力和气氛下，温度曲线变化趋势一致。即当煤颗粒处于干燥阶段时，由于水分的高比热容和高气化潜热，导致在颗粒中心干燥尚未结束时(≤373 K)，颗粒表面温度已经进入脱挥发分阶段，具有相对较高的温度，因此煤颗粒温差峰值均出现在干燥阶段的后期。而当干燥过程结束后，颗粒内外均具有较高的升温速率，颗粒内外温差迅速减小，直至脱挥发分后期温差接近于0。

2.2.2 煤颗粒尺寸的影响

通常，工业流化床锅炉燃烧的煤颗粒尺寸范围较宽(0～13 mm)，不同燃料粒径会对颗粒干燥和脱挥发分产生影响。本研究在4，6，8，10和12 mm粒径下开展，不同粒径热解参数计算结果如图7所示。

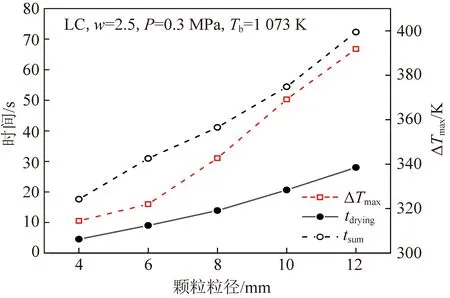
图7 颗粒尺寸对tdrying，tsum和ΔTmax的影响Fig.7 Effect of particle size on the tdrying,tsum and ΔTmax

2.2.3 床层温度的影响

流化床的床层温度是一个十分重要的参数，对燃料颗粒干燥、脱挥发分以及焦炭燃烧过程均有重要影响。本研究计算了流化床增压富氧燃烧条件下不同床层温度(1 023，1 073，1 123，1 173，1 223以及1 273 K)对褐煤颗粒干燥过程和脱挥分过程的影响，计算结果如图8所示。

图8 床层温度对tdrying，tsum和ΔTmax的影响Fig.8 Effect of bed temperature on the tdrying,tsum and ΔTmax

由图8可以发现，随着床层温度的升高煤的tdrying略有下降，tsum和ΔTmax显著降低和升高，这是因为颗粒与床层之间的换热系数增加所致。但是，tsum和ΔTmax随床层温度的变化十分显著，而tdrying随床层温度的变化仅有非常微弱的改变。这是因为当煤颗粒含水分时颗粒的导热系数较低，而干燥后的煤颗粒导热系数会随着温度的升高而增加，这将显著提高颗粒内部的热传递。因此，在干燥阶段，即使床层温度升高，颗粒与环境间换热增强，但由于颗粒内部导热热阻较大，对干燥过程的促进作用也较小。

2.2.4 流化数的影响

流化数是流化床锅炉运行的重要参数，它会影响床层的流动特性和传热传质特性。当CO2气氛、压力0.3 MPa、床层温度1 073 K、颗粒粒径6 mm时，流化数对煤颗粒干燥和脱挥发分过程的影响如图9所示。

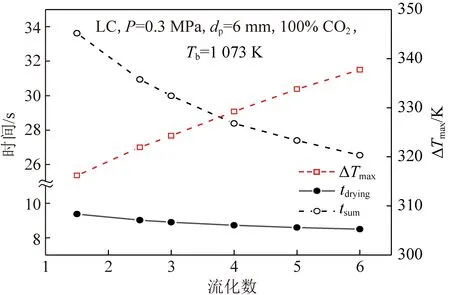
图9 不同流化数对tdrying，tsum和ΔTmax的影响Fig.9 Effect of fluidization number on the tdrying,tsum and ΔTmax

结果表明随着流化数的增加，煤颗粒的tdrying和tsum均有下降，而ΔTmax则明显上升，这是因为随着流化数的增加，颗粒与床层之间的换热系数增加所致。当流化数升高时，一方面煤颗粒周围的床料颗粒更新频率将随之提高，床料与煤颗粒之间的换热将会被加强；另一方面流化数的提高会提高气泡的频率和降低气泡的尺寸[16]，这也将对气-固对流换热系数产生影响，综合表现为流化数越大，总换热系数越大。