UWR-FDTD矿井电磁波数值分析方法

2023-01-07张高敏

煤炭学报 2022年11期

张高敏，刘毅，彭铭

(中国矿业大学(北京) 机电与信息工程学院，北京 100083)

煤矿井下5G、WIFI6、人员定位和车辆定位等无线系统[1]的设计和布置，需进行矿井电磁波分析，以扩大无线基站信号的覆盖范围，提高无线通信质量，节约建设成本。国内外学者用多种方法对矿井电磁波传播特性展开研究[2-6]，但这些方法难以分析巷道中防爆电气开关、机电设备、金属管道、动力和通信线缆等对矿井电磁波传播的影响[7]。时域有限差分(Finite-Difference Time-Domain，FDTD)是计算电磁学中求解麦克斯韦方程组的一种基本方法，该方法自身充分考虑了空间内各种介质对电磁波的反射、衍射、透射的影响以及不同类型电磁波之间的相互作用，使仿真环境更接近实际目标环境，被广泛用于电磁问题的数值仿真[8-10]。

作为一种全波数值分析方法，FDTD需要存储全部Yee网格上的电磁场分量及中间变量，用于时间步迭代，大量的网格以及矩阵运算对计算机内存和算力提出了较高的要求。为了减少内存使用量，提升FDTD的计算效率，扩大FDTD的应用范围，大量学者对此问题进行了深入研究。KATO等[11]通过降低计算空间维度来减少存储需求，在二维球坐标系下用FDTD计算闪电回击通道产生的电场波形。MIGUEL等[12]从共享内存、分布式内存以及矢量化不同CPU体系结构等3个方面研究FDTD并行化计算，得出增加分布式节点，可提高计算性能等结论。MAI等用传统FDTD计算粗网格区域的场值，用弱条件稳定时域有限差分(Weakly Conditionally Stable -FDTD)计算细网格，粗网格和细网格区域交界处采用了空间插值方法来减少仿真时间和内存需求[13]，但过多的插值运算会降低计算精度。何欣波等[14]将Unconditionally Stable FDTD与传统FDTD相结合克服了CFL(Courant-Friedrichs-Lewy)条件限制，由粗网格决定时间步长，在细网格区域及相邻的粗网格区域计算特征值，通过减少特征值分解矩阵大小提高计算效率。DUAN等在电磁波的传播方向上设置一个可移动窗口，可移动窗口内又设置了一个小窗口用来存储大部分电磁场分量，当小窗口到达移动窗口边界时把小窗口数据复制到新的移动窗口开始新区域的计算[15]。AHDAB等[16]为降低计算资源，把全部的障碍物设在激励源附近区域，用FDTD计算出该区域内电磁波相互影响的全部结果，远场电磁波则用抛物线方程计算，BAKIRTZIS等[17]则提出了一种FDTD和射线追踪相结合的电磁波传播方法来降低FDTD的算力需求。

FDTD方法可以分析巷道中防爆电气开关、机电设备、金属管道、动力和通信线缆等对矿井电磁波传输影响。但采用FDTD计算数百米三维立体巷道电磁波传输衰减，对计算设备的内存、算力都提出了非常高要求，制约了FDTD在矿井电磁波衰减仿真的应用。针对煤矿井下巷道断面小，轴向长的特点，笔者提出了单位窗口循环使用的时域有限差分方法(Unit Window Recycling，UWR-FDTD)。该方法沿巷道轴向把整个巷道均匀划分成多个大小相同的虚拟窗口，仅为一个与虚拟窗口大小相同的单位窗口分配内存空间，所有虚拟窗口根据自身编号循环使用单位窗口内存进行FDTD迭代，每一个虚拟窗口迭代完成后，存储单位窗口电磁场，用于合成整个巷道内的电磁场。UWR-FDTD方法不改变FDTD的迭代方程，可根据计算机硬件设定单位窗口大小，划分窗口个数，FDTD迭代过程仅在一个单位窗口的内存空间内进行，大幅减少了传统FDTD方法对内存的需求，提高了计算效率。

1 UWR-FDTD建模

1.1 FDTD原理

麦克斯韦方程组揭示了电和磁之间的转换规律，预测了电磁波的存在。FDTD直接求解麦克斯韦方程组研究电和磁之间的关系，成为计算电磁学中的一个重要数值计算方法[18]。FDTD把计算空间划分成多个Yee网格，电场可以设置在Yee网格棱的中心，磁场在Yee网格面的中心，这样每个电场分量周围都环绕4个磁场分量，每个磁场分量也环绕着4个电场分量，与自然界中电场与磁场的物理结构保持一致。由于电场与磁场在时间和空间上都交叉分布，迭代过程也很容易用差分格式实现。用麦克斯韦方程组的两个旋度方程，在时间和空间上差分可以推导出FDTD的迭代方程[19]。

(1)

式(1)中的E和H在直角坐标系下沿x，y，z三个方向可以拆分成关于Ex，Ey，Ez和Hx，Hy，Hz的6个标量方程。设定空间离散步长和时间离散步长，把上述6个标量方程中关于x，y，z，t的偏导数用中心差分近似后，即可得到电磁场在x，y，z三个方向分量上FDTD显示表达式。FDTD的计算空间包括待仿真的全部空间以及空间内的激励源和散射体，空间离散步长一般小于待研究频域内最短波长的1/10[16]。受计算机内存容量限制，在模拟无限大区域内的电磁特性时，还需要在相应的截断边界处给出吸收边界条件[21]。

1.2 UWR-FDTD模型

对于断面为拱形或马蹄形的矿井巷道可以用面积等效为一个矩形巷道，故在直角坐标系下设等效矩形巷道断面宽和高的大小分别为lx，ly，巷道轴向长lz，3个方向Yee网格空间步长均为δ。UWR-FDTD仿真时，用激励源模拟发射天线，可以把电磁波信号通过更新方程耦合到空间网格内。激励源所在的巷道断面为轴向起始参考位置，一般情况下激励源位于巷道断面中心，激励源在巷道断面上的不同位置可以研究发射天线位置对矿井电磁波传播特性的影响。沿巷道轴向把巷道划分成多个长度大小均为lwz并从1顺序编号的虚拟窗口，虚拟窗口的断面大小与巷道的断面大小相同。单位窗口中lwz的大小可根据计算机硬件性能和巷道轴向长度lz的大小来设定，一旦确定lwz后对计算结果向上取整，得单位窗口的数量nw：

(2)

仿真时，整个计算空间只需为电场和磁场分量及中间变量分配一个单位窗口的存储空间用于FDTD迭代过程、与电磁波传播lwz距离所用时间Tu相关的缓存空间。实际计算的巷道空间在3个方向上的大小分别为lx,ly和lz×nw，整个FDTD迭代过程在一个单位窗口空间内完成。电磁波在一个单位窗口内沿z方向的传播时间Tu为

(3)

式中，Δt为Yee网格的时间步长。

电磁波从激励源经过Tu时间到达单位窗口z方向的最后一个Yee网格，在此之后需要存储最后一个网格的电场和磁场分量作为下一个虚拟窗口迭代的激励源。

针对三维矿井巷道特点提出的UWR-FDTD方法同样适用于一维和二维空间。使用UWR-FDTD方法对一维空间仿真时，Yee网格可比作一个点的扩展，需要按照时间步存储最后一个点的各电场和磁场分量作为下一窗口迭代的子激励源。若使用UWR-FDTD方法对二维空间进行仿真时，Yee网格可比作一条线的扩展，需要按照时间步存储最后一条线的各电场和磁场分量作为下一窗口迭代的子激励源。同理使用UWR-FDTD对三维空间进行仿真，Yee网格可作为一个面的扩展，需要按照时间步存储最后一个面的各电场和磁场分量作为下一窗口迭代的子激励源。电磁波在空气介质中以近似光速从激励源到达第一个窗口最后一个Yee网格的时间为Tu，并且激励源以固定频率周期变化，计算空间内各位置的电磁场也将呈周期性变化，在此可缓存单位窗口内最后一个网格Tu/Δt个时间步的电磁场作为下一个虚拟窗口的激励源。每一个单位窗口运行完最后一个时间步长后都把该窗口的电场各分量转存到合成电场中。UWR-FDTD的基本原理如图1所示。

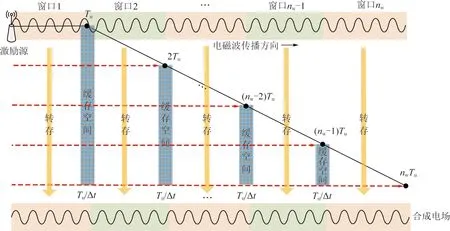
图1 UWR-FDTD原理Fig.1 Principle of UWR-FDTD

为避免FDTD多个时间步迭代后的仿真结果发散，空间离散步长和时间离散步长上需要满足CFL稳定性条件[19-20]：

(4)

若网格3个方向上的空间步长均为δ，则式(4)可简化为

(5)

S=cΔt/δ

(6)

1.3 边界处理

在直角坐标系中用x，y，z三个方向电场矢量和(下文用x方向表示计算空间的宽度方向，y方向表示高度方向，z方向表示长度方向)表示Yee网格的合成电场，该电场选在Yee网格的左下角。在两个虚拟窗口或传播介质与PML吸收边界的交界面上，若使用左下角合成电场表示边界处的电场，用最后一个Yee网格的电场表示传播介质和PML交界处的电场，则存在一个Yee网格空间步长的计算误差，如图2中用Em(1,1,nm)表示第nm个网格的电场情况。因此，需要对边界处的电场进一步处理，减小该误差。边界电场处理方法如图2所示。

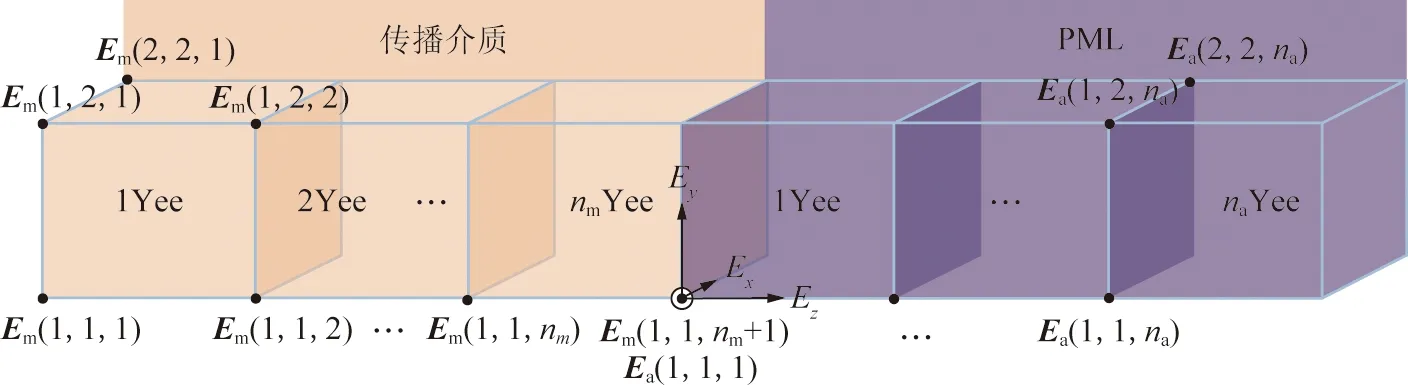
图2 边界电场处理方法Fig.2 Treatment method of boundary electric fields

图2中传播介质空间和PML空间沿x,y方向都包含nxny个Yee网格，传播介质空间沿z方向分别被划分为nm个网格，PML包含na个网格。传播介质空间和PML空间第1个Yee网格的电场分别为Em(1,1,1)和Ea(1,1,1)，传播介质中最后一个Yee网格电场为Em(1,1,nm)。可以近似求解Em(1,1,nm+1)的值当作传播介质和PML交界面处的电场，以及进入PML层的初始电场Ea(1,1,1)，实现减少1个空间网格步长的误差。FDTD迭代过程可得在两种介质交界面上x和y方向上的电场Emx(1,1,nm+1)和Emy(1,1,nm+1)，由于Emz(1,1,nm+1)在PML空间无法用传播介质空间的电磁场分量直接计算，并且电磁波进入到PML空间后电磁场强度的衰减速率按照指数增加，在此采用传播介质中Emz(1,1,nm-1)和Emz(1,1,nm)的线性插值表示Emz(1,1,nm+1)。可得在交界面上沿坐标轴3个方向上的电场为

(7)

2 数值计算与分析

本文实验仿真软件为Matlab R2021a，操作系统为Windows 10 专业版，CPU型号为Intel(R) Core(TM) i7-7700K CPU @ 4.20 GHz，系统内存容量32 GB。在此设计不同的实验场景从计算精度与计算效率2个方面对比UWR-FDTD和传统FDTD的数值计算性能，并研究UWR-FDTD中窗口大小与仿真时间之间的关系。

2.1 内存空间

煤矿巷道壁材料主要为混凝土，其电磁参数变化不大，可以等效为各向同性的一个狭长的计算空间。设巷道断面大小为nxny个Yee网格，轴向长为nz个Yee网格，所需电磁场各分量及中间变量个数为ne，则传统FDTD所需内存空间κFDTD为

κFDTD=nxnynzne

(8)

(9)

单位窗口内循环计算出的电场分量最后要合成整个巷道的电场，因此还需要分配一个额外内存空间存储整个巷道内的电场κa，大小为

κa=nxnynz

(10)

由式(9)和(10)可得UWR-FDTD所需的全部内存空间κUWR为

(11)

式(8)给出了传统FDTD所需的内存空间，用式(11)除以式(8)可得UWR-FDTD所需的内存空间与传统FDTD所需内存空间的比值，经过化简后为

(12)

由式(12)可知ζ的大小与划分窗口的个数以及电磁场及中间变量的个数有关。

下面在一维二维三维空间内分别分析。根据FDTD更新方程，一维计算空间需1个电场和1个磁场变量，用指数差分BerengerPML吸收边界条件至少需4个系数变量，故ne≥6。二维计算空间需2个电场、2个磁场变量、至少4个参与FDTD迭代的系数变量，故二维计算空间中ne≥8。对于三维计算空间，电磁场将分裂成12个电磁场变量，以及至少4个系数变量，故三维计算空间中ne≥16。不同维度空间所需的变量个数不同，划分不同窗口数量时UWR-FDTD方法和传统FDTD方法所需内存的比值见表1。

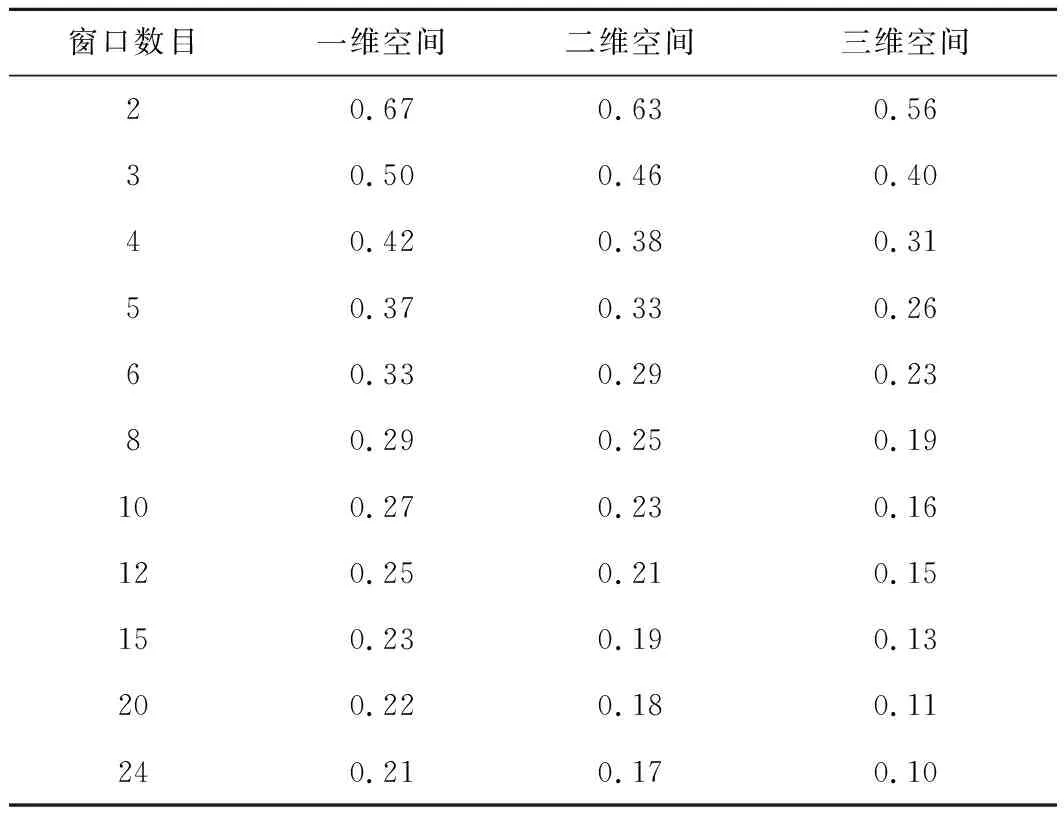
表1 不同维度空间下ζ的大小

从表1可知，与传统FDTD方法相比，用UWR-FDTD方法划分的窗口数目越多，仿真时所需的内存空间越小；在三维计算空间内使用UWR-FDTD方法求解电磁问题时，节省的内存空间远大于一维和二维计算空间。

2.2 计算精度

FDTD仿真过程需要用与时间相关的函数作为激励源引入到计算区域，常用周期时谐函数和脉冲函数作为时谐源和脉冲源。时谐源带宽窄，一次可以仿真一个频点的电磁波，但可以直观的看出电磁波的传播特性。脉冲源具有宽频带特性，使用脉冲源进行一次FDTD仿真，可以得到较宽频带上的电磁响应特性[22]。在此采用正弦波作为时谐源，微分高斯脉冲作为脉冲源对UWR-FDTD方法的性能进行分析，2种激励源时间变化的函数方程为

(13)

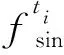
对于式(13)中的微分高斯脉冲，当t0=τ且fmaxτ=2(fmax为微分高斯脉冲中待分析的最高电磁波频率)，可以用稳定因子S和单位波长包含的Yee网格数量dλ把Δt隐式表示，微分高斯脉冲可以离散为

(14)

在一维空间内待求计算空间长度为5 m，窗口长度为2 m，根据UWR-FDTD方法整个计算空间将被划分为3个窗口，实际计算空间长度为6 m。Yee网格空间步长为载波波长的1/20[23]，CFL稳定因子S为0.5，采用10层指数差分Berenger PML吸收边界条件。以激励源位置为起始点，用900 MHz的正弦波激励源和微分高斯脉冲激励，在无耗介质中迭代720时间步后电场的时域波形如图3所示。由于迭代720时间步电场刚传播到整个计算空间的最后一个网格，正弦波激励源最右侧电场还没有完全稳定，使用UWR-FDTD方法划分3个窗口合并后的电场与传统的FDTD方法计算出的电场一致性较好，在2，4 m等2个窗口的交界处合成电场较为平滑。同一计算空间微分高斯脉冲激励源在无耗介质中用UWR-FDTD和FDTD方法计算出的时域电场波形也几乎完全一致。

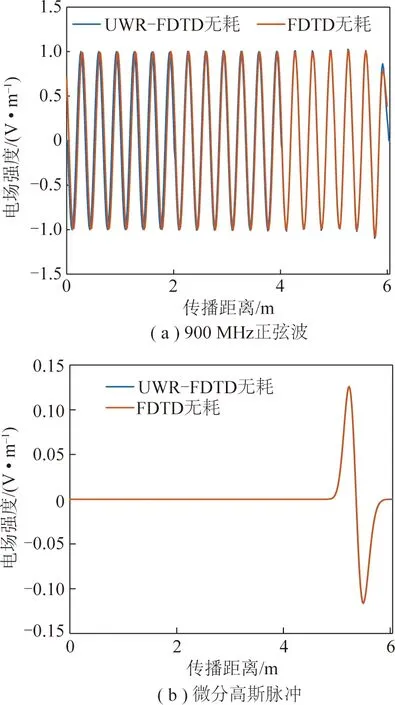
图3 一维无耗介质中的时域电场Fig.3 Time domain electric field in one-dimensionallossless medium

同无耗介质计算空间大小一样，设有耗介质电导率σ为0.36 S/m，900 MHz正弦波和微分高斯脉冲激励源传播6 m，划分3个窗口的UWR-FDTD与FDTD方法计算出的时域电场波形也一致，如图4所示。

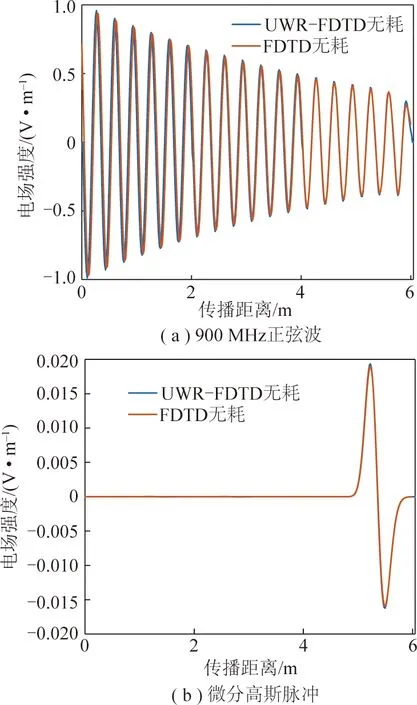
图4 一维有耗介质中的时域电场Fig.4 Time domain electric field in one-dimensional loss medium

在长10 m、宽4 m的二维无耗介质计算空间中，设置UWR-FDTD单位窗口长3 m，宽4 m，可知需要把计算空间划分4个虚拟窗口，实际计算空间长12 m、宽4 m。设正弦激励源频率为900 MHz，Yee网格空间步长16.67 mm，CFL稳定因子为0.5，时间步长27.8 ps，窗口四周采用10层指数差分BerengerPML吸收边界条件。激励源位于计算空间宽度方向上的中心位置，从激励源开始在整个二维无耗计算空间内沿计算空间长度方向的时域电场分布如图5所示。图5(a)，(b)为2种方法求解出在整个二维空间内的瞬时电场强度分布情况，图5(c)为接收点位于宽度方向上的中心位置，沿巷道长度方向上各空间采样点处的瞬时电场强度。

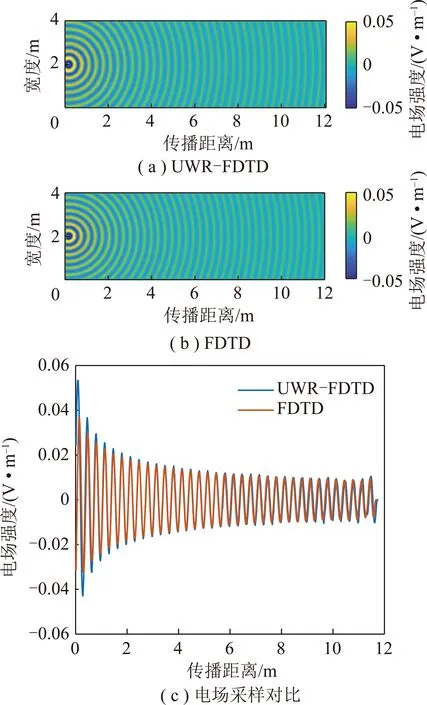
图5 二维无耗介质中的时域电场Fig.5 Time domain electric field in two-dimensionallossless medium

由图5可以看出，UWR-FDTD方法划分4个窗口单独运行后再合成的电场分布，与在一个窗口内使用FDTD运行的电场分布，在幅值和周期两个方面都能较好吻合，表明UWR-FDTD能够在二维计算空间内取得较好计算结果。

用文献[2]中高3.4 m、宽4.8 m的一个等效矩形巷道来仿真三维无耗计算空间，窗口四周采用10层指数差分BerengerPML吸收边界条件。当正弦激励源频率为900 MHz时，波长为333.11 mm，CFL稳定因子为0.40时，时间步长为22.22 ps，Yee网格空间步长为电磁波波长的1/20，对应单位窗口宽高分别288和204个Yee网格空间步。把偶极子激励源放在巷道断面中心，设单位窗口长为300个Yee网格，巷道长度约为5 m，用传统FDTD与UWR-FDTD两种方法，对3个虚拟窗口组成的巷道和5个虚拟窗口组成的巷道进行仿真，接收位置同样位于巷道断面中心沿巷道轴向采样，最终得到各采样点处的合成电场时域波形如图6所示。

由图6可知，在三维巷道内，用UWR-FDTD与传统FDTD方法计算出的电场大小和周期较为一致，划分多个虚拟窗口分别计算，最后合成的波形在2个窗口过渡时较为平滑，无明显窗口分割痕迹。经过在不同维度空间对UWR-FDTD方法计算精度的分析可知，该方法可用于煤矿井下、金属和非金属等其他矿井、铁路隧道、公路隧道、地铁、地下人防工程、城市地下管廊、地下商场等空间内的电磁波分析。

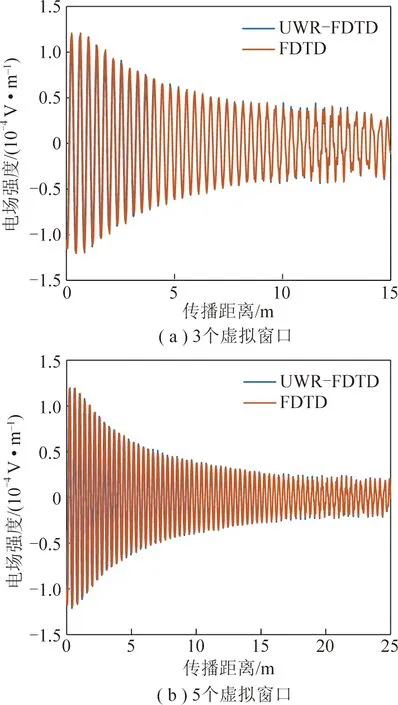
图6 三维无耗介质中时域电场Fig.6 Time domain electric field in three-dimensionallossless medium

2.3 计算效率

UWR-FDTD方法把计算空间分割成多个虚拟窗口，电磁场分量及中间变量矩阵大小和单位窗口大小相同。传统FDTD在1个时间步内迭代整个计算空间的电磁场变量矩阵，两者相比，UWR-FDTD在每个时间步的计算量大幅减小，理论上可以缩短仿真时间，提高计算效率，下面在三维巷道内用仿真实验给予验证。

《煤矿安全规程》第九十条和《煤矿巷道断面和交岔点设计规范》4.1.1节规定了轨道机车运输的巷道净高自轨道道面起不得低于2 m，采(盘)区内上山、下山和平巷的净高度不得低于2m，薄煤层内不得低于1.8 m，巷道净宽不宜小于2.0 m。用900 MHz正弦波作为激励源，稳定因子S取0.4，空间步长为电磁波波长的1/20，约为16.67 mm。设巷道断面宽高分别为140，110个Yee网格，约为2.33 m和1.84 m，单位窗口长为140个Yee网格约为2.33 m。测试从1到22个单位窗口组成的三维巷道，长度从2.33 m到51.33 m，在上述不同长度的巷道内用UWR-FDTD和FDTD两种方法仿真同一电磁波传播问题，仿真过程所需时间如图7所示。

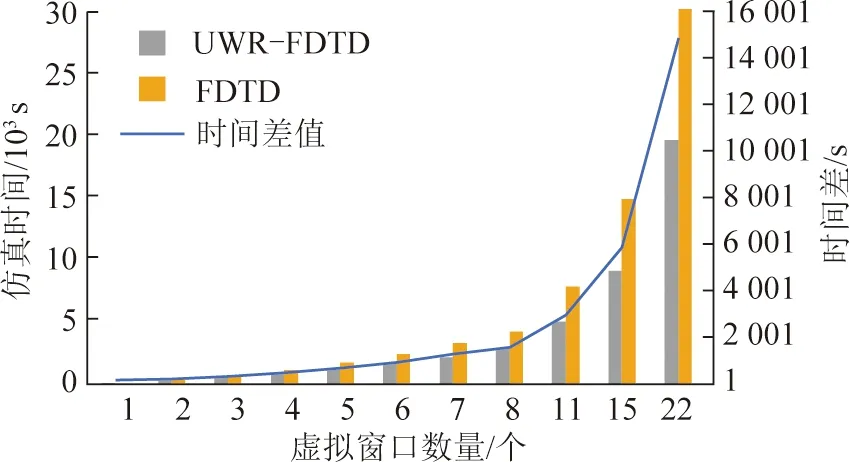
图7 不同三维空间的仿真时间Fig.7 Simulation time in different three-dimensional spaces

当单位窗口长度和待仿真巷道长度相等时，相当于没有划分窗口，2种方法的仿真时间都为74 s，时间差为0，说明UWR-FDTD在不划分窗口时与传统FDTD的计算方法本质相同。当计算空间大小为8个虚拟窗口时，UWR-FDTD方法仿真用时2 739 s，FDTD方法仿真用时4 149 s，两者用时相差1 410 s。当计算空间长度为22个虚拟窗口时，UWR-FDTD方法仿真用时19 499 s，FDTD方法仿真用时34 335 s，UWR-FDTD方法所需仿真时间比FDTD减少了14 836 s，降低了43.2%。故，UWR-FDTD方法非常适合狭长空间的电磁问题数值仿真，计算空间越大，同FDTD相比UWR-FDTD方法的计算效率越高。

2.4 窗口大小优化

对于同一段巷道，单位窗口的大小决定了需要划分虚拟窗口的数量，虚拟窗口数量又决定着每个虚拟窗口在单位窗口内的迭代次数，迭代次数进一步影响整个巷道的仿真时间。因此需要研究巷道断面的大小、巷道长度、电磁波频率等多个条件下，虚拟窗口数量与仿真时间之间的关系，给出最优单位窗口大小的计算方法。

2.4.1 巷道断面

用900 MHz正弦激励源模拟发射天线，激励源位于巷道断面中心，Yee网格空间步长为波长的1/20，巷道长(z向)1 200个Yee网格，沿长度方向分别划分为2，3，4，5，6，8，10，12，15，20，24个窗口，用xy表示巷道宽和高的Yee网格数量。当xy分别为140×110,90×70和50×40时，仿真上述11种虚拟窗口划分方法所需的仿真时间见表2。

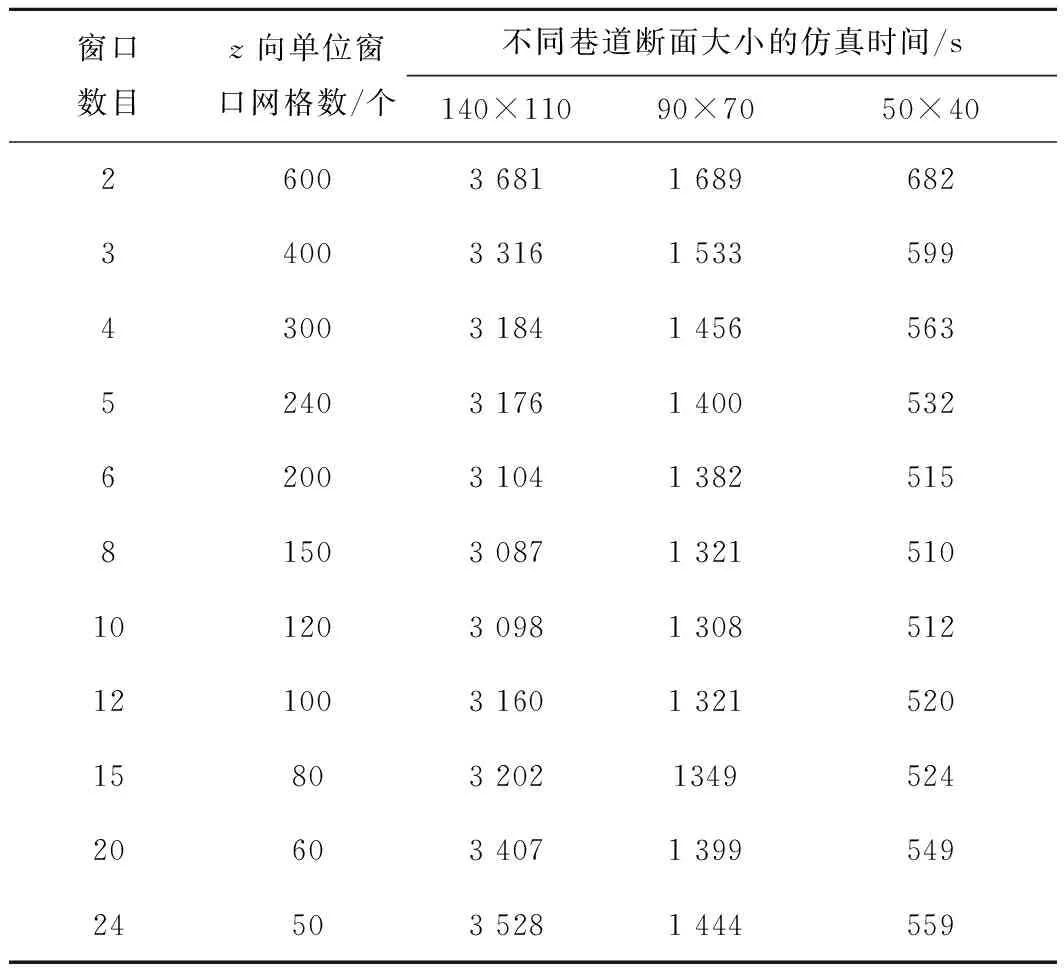
表2 不同巷道断面大小的仿真时间

取表2中每一种xy仿真时间最小的一个虚拟窗口为时间基准(加粗数据)，其他虚拟窗口的仿真时间都减去基准虚拟窗口的仿真时间，可得虚拟窗口数量、xy大小与仿真时间之间的关系，如图8所示。

由图8可以看出，对于同一长度的巷道，不管xy大小如何，划分虚拟窗口数量过多或过少都会增加仿真时间，并且xy越大，划分虚拟窗口的数量对仿真时间的影响越大。长度为1 200个Yee网格的巷道划分8～10虚拟窗口时所用的仿真时间相对较少，此时单位窗口的长度为总巷道长度的1/10～1/8。

2.4.2 巷道长度

激励源、稳定因子和吸收边界条件与2.4.1节中设定的数值相同，巷道断面固定为140×110个Yee网格，巷道长度分别为1 200，840和720个Yee网格。每种长度巷道依旧划分为2，3，4，5，6，8，10，12，15，20，24个虚拟窗口，使用UWR-FDTD方法仿真上述不同长度巷道所需的仿真时间见表3。

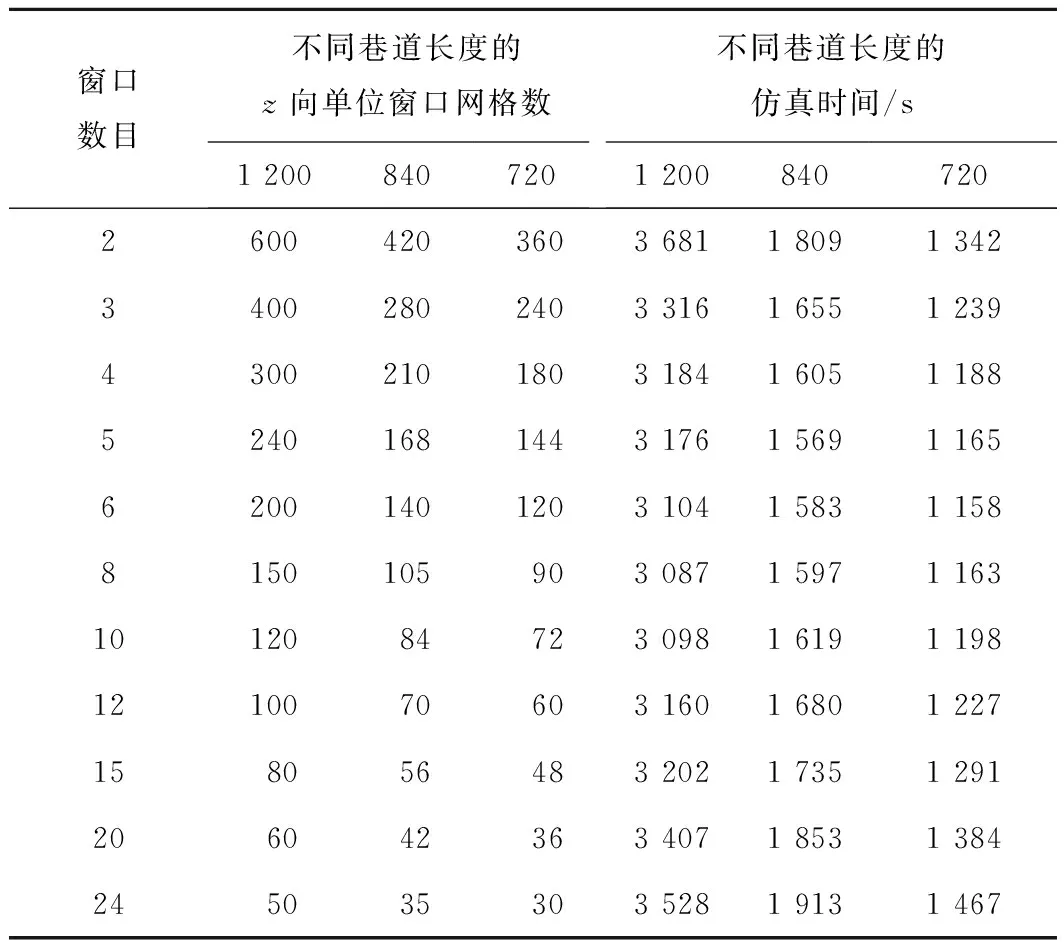
表3 不同巷道长度的仿真时间

由表3可知，巷道长度方向Yee网格大小为1 200和840时，把上述巷道划分为8个和5个虚拟窗口所需仿真时间最短；长度为720个Yee网格，划分6个虚拟窗口时所需仿真时间最短。根据表3数据，以仿真时间最短的虚拟窗口为基准(加粗数据)，其他虚拟窗口的仿真时间都减去基准窗口的仿真时间，可得不同巷道长度与仿真时间的关系，如图9所示。

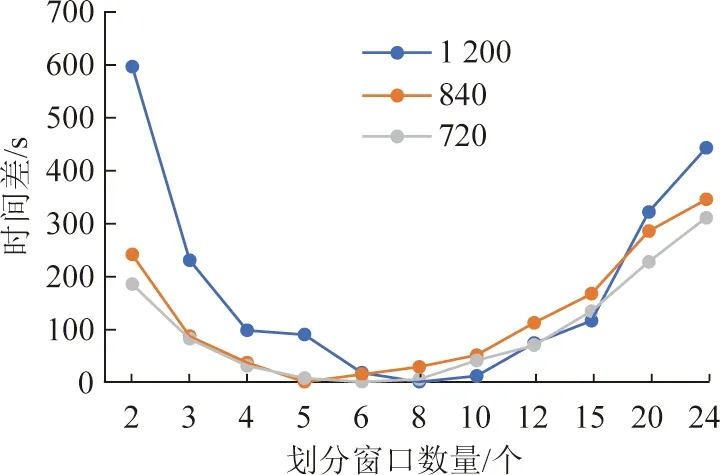
图9 巷道长度与仿真时间的关系Fig.9 Relationship betweentunnel length and simulation time

由图9可知不管待计算的巷道有多长，划分虚拟窗口数量过多或过少都会增加仿真时间。对于同一xy断面，单位窗口长度为对应巷道长度的1/10～1/6时，所需仿真用时相对较小。

2.4.3 电磁波频率

用1 200，900，700 MHz的正弦波作为激励源在长×宽×高为840×90×70个Yee网格的巷道内仿真，网格步长都为电磁波波长的1/10，计算不同电磁波频率在划分不同窗口数量时所需的仿真时间，统计划分窗口数量与电磁波频率之间的关系。3种电磁波频率划分不同窗口数量时所用的仿真时间见表4。

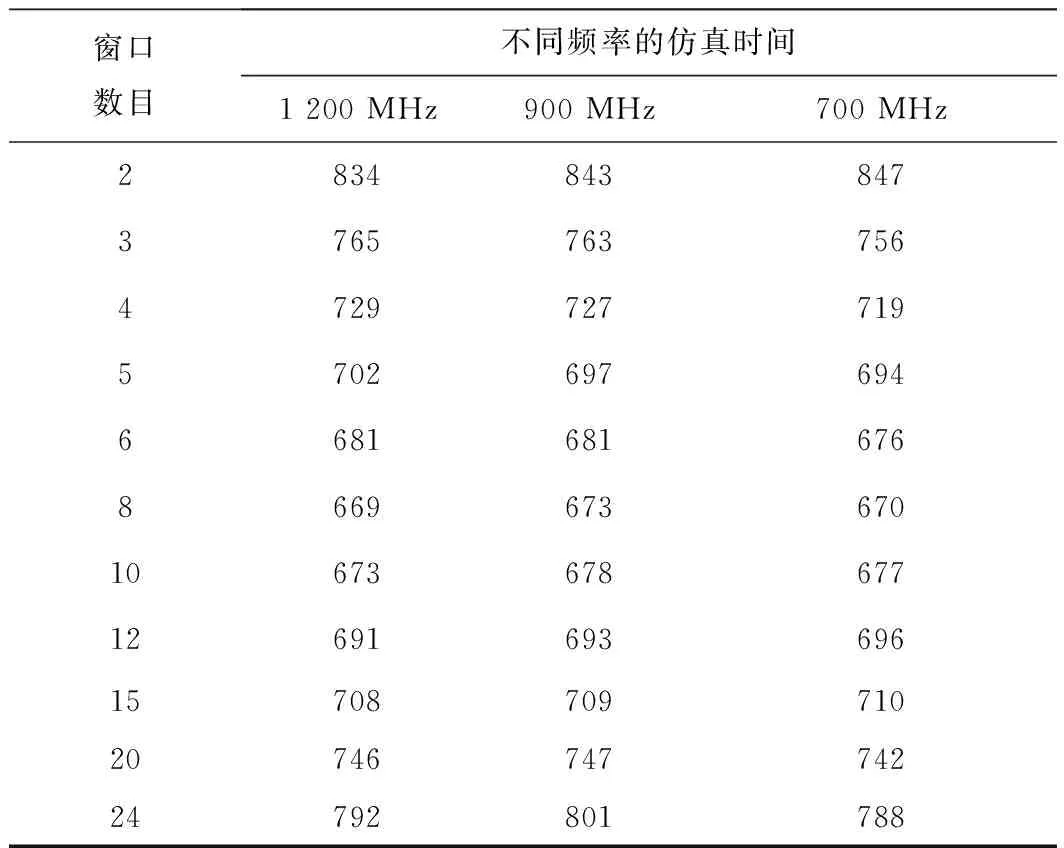
表4 窗口数量与不同频率的仿真时间

每个频率中选择用时最少的虚拟窗口作基准(加粗数据)，该频率中其他数目虚拟窗口的仿真时间减去基准窗口的时间，可得不同电磁波频率对仿真时间的影响程度，如图10所示。3条不同电磁波频率的时间差曲线几乎完全重合，说明UWR-FDTD方法在相同数量网格内所需的仿真时间与电磁波频率无关，但划分虚拟窗口的数量与仿真时间关系较大。当计算空间被分为8个虚拟窗口时，3种频率都能在最短的时间内完成数值仿真，此时单位窗口长度为计算空间总长度的1/8。

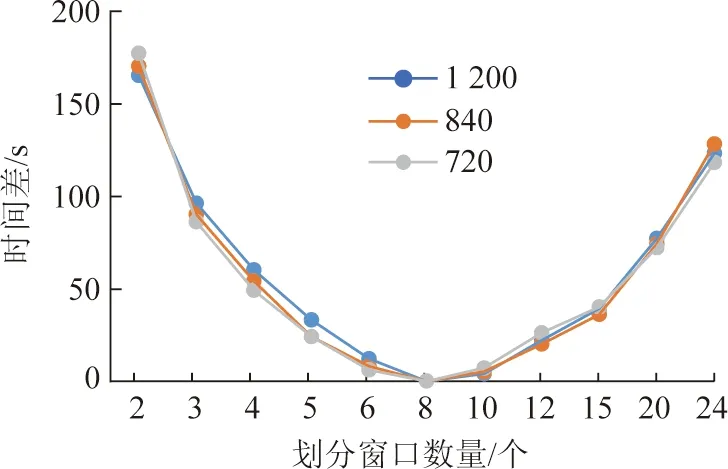
图10 窗口数量和频率与仿真时间的关系Fig.10 Relationship between electromagnetic wavefrequencies and simulation time

综上所述，从巷道空间分析最优单位窗口的划分方法，由图8可知,不同巷道断面单位窗口长度为巷道总长度的1/10～1/6内时，仿真时间最短；由图9可知对于不同巷道长度，单位窗口长度也是在上述取值范围内仿真时间最短。可得出在同一计算空间内，单位窗口长度为计算空间总长度的1/10～1/6时仿真计算用时最短。对于不同电磁波频率，从图10中可得当单位窗口长度为计算空间总长度的1/10～1/6时，计算效率较高。因此，在同一巷道内，不管电磁波频率多大，当单位窗口长度为计算空间总长度的1/10～1/6时，都能取得较好的计算效率。