玻璃喷气冷却传热特性及影响因素

张晓宇 刘风肖 石发祥 迟勃洋 田亮 赵聚龙

（1. 河北工业大学校园建设与管理处 天津 300401；2. 河北工业大学能源与环境工程学院 天津 300401）

0 引言

玻璃以其良好的透明性得到了广泛应用，但玻璃表面微缺陷的存在导致其容易破碎。为了提高玻璃的强度，各种玻璃钢化技术应运而生。目前玻璃钢化方法主要有物理钢化和化学钢化［1］，其中物理钢化方法中最常用的工艺为喷气冷却，即采用高速空气对高温玻璃进行急速冷却［2］。该过程使玻璃内外产生温度梯度，从而产生应力层，以获得足够的强度［3］。

玻璃喷气冷却钢化过程中，很多工艺参数会影响玻璃的换热过程，从而影响其钢化质量。因此，许多学者针对玻璃冷却过程及工艺控制进行了大量研究。许伟光［4］着眼于温度控制工艺，指出其在钢化玻璃生产过程中的重要地位。夏国华等［5］运用非线性的有限元法，模拟了平板玻璃钢化过程，得到玻璃中心和边界区域的温度分布和应力的变化历史及分布。岳高伟等［6］建立了玻璃降温的风栅模型，分析了风压、风温、玻璃出炉速度和玻璃摆动速度对玻璃降温规律的影响。F.Monnoyer等［7］对玻璃钢化的撞击式空气射流过程进行模拟，评估了从玻璃表面到冷却喷嘴之间的对流传热，计算了四种不同的雷诺数的射流传热系数。研究发现，局部传热与平均传热的相对偏差与雷诺数无关，平均努赛尔数与雷诺数存在幂数关系。Cirillo等［8］采用计算流体力学模拟的实验设计矩阵，建立了垂直撞击平板的九个圆形受限空气射流的传热系数的数学模型，分析了玻璃钢化中常用的设计参数值的平均传热系数和冷却过程均匀性。Puneet Gulati等［9］研究了喷嘴形状、射流间距和雷诺数对光滑表面上垂直冲击淹没空气射流局部传热分布的影响，得出圆形射流的压力损失系数最低，矩形射流的压力损失系数最高。雷诺数对于非圆形射流性能的影响与圆形射流相似，随雷诺数的增加，换热速率增加，且平均努赛尔数对喷嘴形状不敏感。Yazici［10］利用方形和三角形排列的多喷嘴确定不同雷诺数下4 mm厚平板玻璃在自动玻璃钢化中的最佳快速冷却配置，发现在三角形排列喷嘴系统中获得最佳钢化条件。

综上所述，钢化工艺参数是影响玻璃传热特性及钢化质量的重要因素。由于气冷钢化过程中玻璃内部的温度难以实时测量，因此若通过反复实验来优化钢化工艺参数，导致产品开发周期长、成本高，难以保证高产品质量［11］。因此，本文对玻璃喷气钢化过程进行了数值模拟，研究了玻璃在喷气钢化过程中的换热特性，并分析了射流速度、喷孔到玻璃距离、喷孔间距以及喷孔排布方式对玻璃降温规律及温度均匀性的影响，为钢化玻璃生产过程中冷却工艺参数设置提供理论依据。

1 模型建立与数值模拟

1.1 物理模型

本文对尺寸为40 mm×40 mm×5 mm玻璃的喷气钢化过程进行数值仿真，物理模型如图1所示。

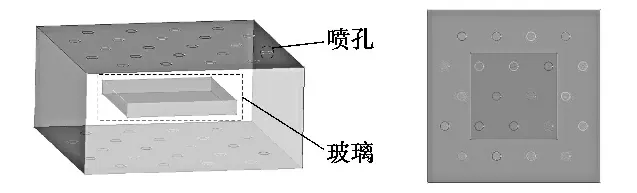
图1 淬冷玻璃几何模型

喷孔呈等边三角形排布，其直径D为4 mm。喷孔与喷孔之间的距离S为16 mm，喷孔到玻璃的距离H为16 mm，即S/D＝4，H/D＝4。为避免边界效应对计算结果产生影响，计算域尺寸为80 mm×80 mm×37 mm。采用ICEM软件对计算域进行结构化网格划分，如图2所示。

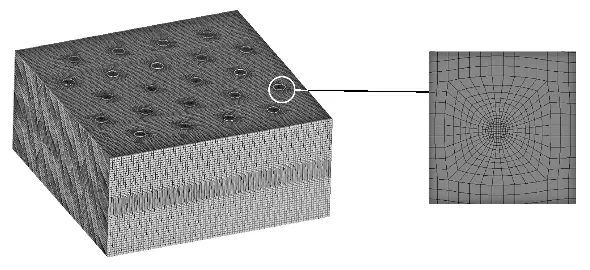
图2 模型网格划分

为了提高计算精度，对玻璃板附近及喷孔处网格进行细化。在玻璃钢化过程中，材料性质随温度发生显著变化。玻璃的密度固定为2500 kg/m3，其他性质见表1。

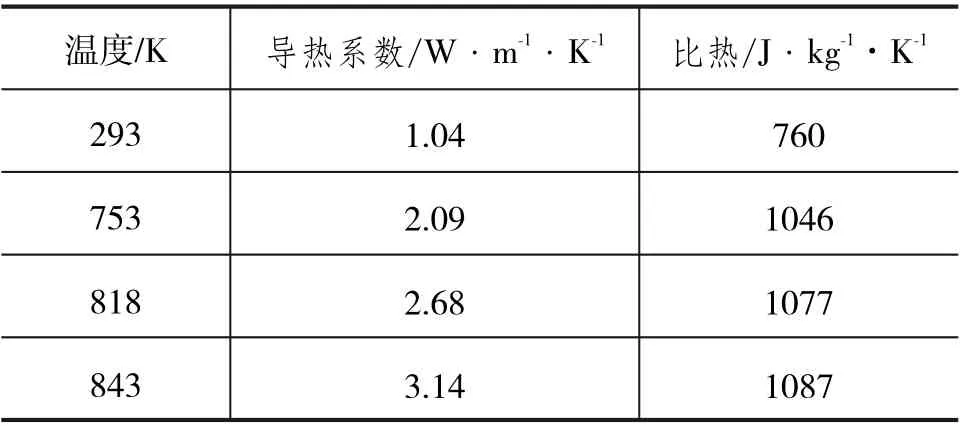
表1 玻璃性质［12］

1.2 数学模型

此次数值模拟基本控制方程式为：

（1）连续性方程

（2）动量方程

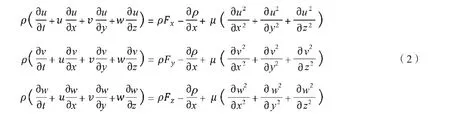
本研究选用了K-epsilon模型中的realizablek-e model湍流模型，因为其可以更好地模拟圆形射流问题。

鉴于圆形喷嘴对玻璃板上的喷气冲击，关于模型的假设为：

（1）这是一个瞬态传热过程；

（2）流体（空气）的性质是恒定的；

（3） 流体（空气）是不可压缩的；

（4）玻璃表面光滑。

1.3 边界条件

（1）喷孔为速度入口，流动速度为80 m/s，湍流强度为5%，入口温度恒定为300 K；

（2）周围出口为压力出口，出口压力与环境压力相同；

（3）玻璃板的表面为流固耦合边界，玻璃的初始温度为893.15 K。

2 玻璃钢化过程中的换热特性

玻璃表面平均传热系数和温度随时间的变化如图3所示。

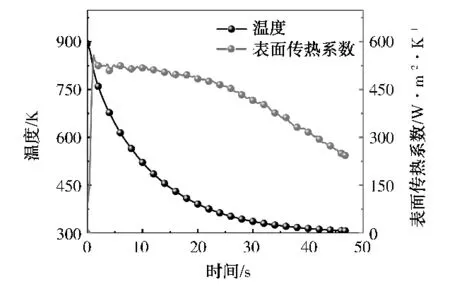
图3 玻璃表面传热系数和温度变化

由图3可以看出，玻璃表面冷却速率随时间呈负指数的降低，而并非线性降低。同样，玻璃表面传热系数在冷却初期时呈最大值，而后随时间降低。这是因为在淬冷初期，玻璃温度较高，与空气的温差最大。随冷却的进行，玻璃温度降低，导致玻璃表面与空气的温差减小。

图4为玻璃板中心点与表面中心点随时间冷却的温度历史和温差变化。

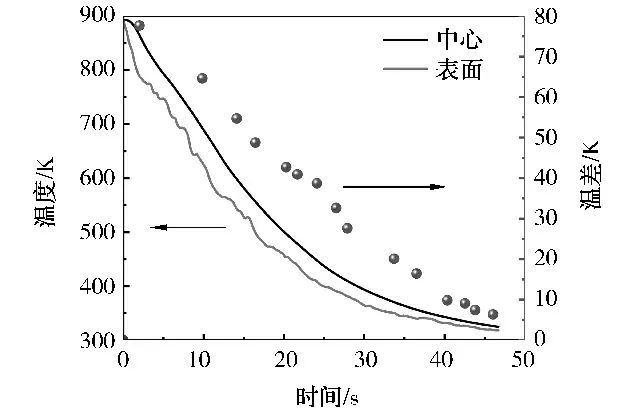
图4 玻璃板中心点与表面中心点温度变化及两点温差变化

由图4可知，玻璃表面温降比内部大；在玻璃厚度方向，最初几秒内温差迅速增加，并在t＝5 s时达到最大值，然后逐渐减小，趋近于0。这是由于开始淬冷时，玻璃表面对流换热量远远大于内部导热量，随着玻璃内外温差变大，内部导热量增加，使玻璃内外温差变小。根据无限板的推导，Adams等［13］提出了玻璃钢化过程中内应力与冷却速率之间的关系：

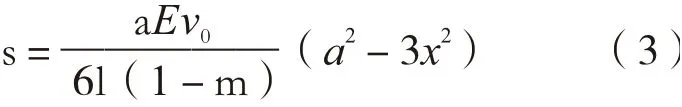
式中：s——玻璃的内应力；

a——膨胀系数；

E——弹性模量；

l——导热性；

m——泊松比；

v0——冷却速率；

a——玻璃板厚度的1/2；

x——测量点的距离。

根据式（3）可以看出，由于冷却速率不同，导致玻璃内外存在温差，从而产生热应力。因此，根据玻璃冷却过程中最大温差值可以判断玻璃的钢化程度。

在玻璃钢化过程中，玻璃厚度方向上的温差决定了玻璃内部的应力大小，而玻璃表面温度的均匀性决定了钢化玻璃质量的优劣［14］。图5为玻璃瞬时温度云图分布，该图表明在淬冷过程中，玻璃表面存在明显的温度梯度，呈现出非均匀性。玻璃的四角温度最低，这是因为玻璃顶点与周围环境的接触面积最大，对流传热速度最快［15］。因此，在进行玻璃钢化时，玻璃顶点处容易因冷却过快而应力集中，导致其破碎。其次，滞止区温度最低，这是由于喷孔的射流冲击。

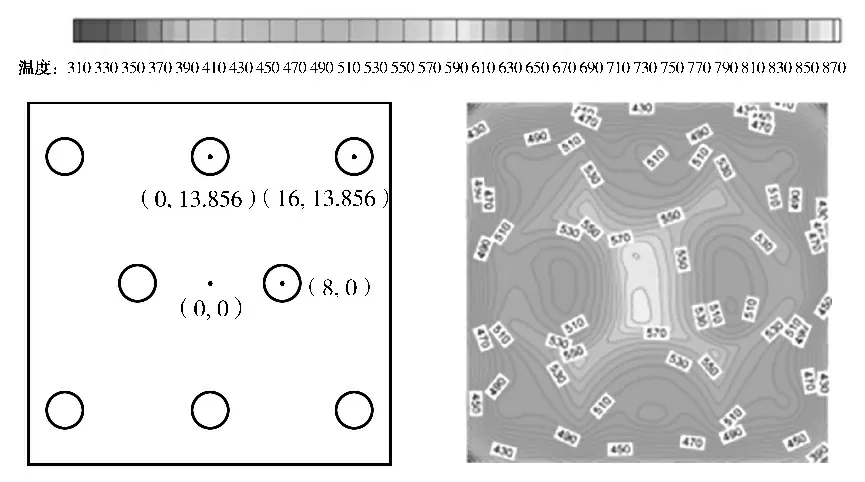
图5 t ＝ 11 s时的温度分布

3 淬冷钢化玻璃降温影响因素分析

钢化玻璃过程中的影响因素众多，主要有喷气射流速度、喷嘴到玻璃的距离、喷孔间距、喷孔排布方式。基于上述淬冷玻璃物理模型，利用仿真模拟分析各因素对玻璃降温速率和温度均匀性的影响。

3.1 喷气射流速度

喷气射流速度是影响玻璃钢化程度和钢化效果最为重要的工艺参数之一。为了分析喷气射流速度对高温玻璃降温规律的影响，设置射流速度分别为40、60和80 m/s。

图6中实线表示玻璃表面温度随时间的变化，虚线代表玻璃中心点与表面中心点温差的变化规律，该图表明随射流速度的增大，玻璃的降温速率和最大温差均增大，并且最大温差出现的时刻逐渐提前。这是由于射流速度越大，玻璃近壁面处的扰动增强；并且冷风质量流量也随之增高，使玻璃对流换热效率增强、玻璃内外温差增大。因此，可通过调高射流速度的方式提高玻璃钢化应力。

图6 玻璃表面平均温度以及玻璃中心点和表面中心点温差的变化规律

图7显示了玻璃表面温度分布，玻璃表面边缘处和滞止区温度总是最低的，在玻璃表面的中心区域存在一个最高温度区，并且该区域的温度值随风速的增加而降低。将玻璃表面上最高和最低温度之差定义为表面最大温差（DT），用来说明玻璃表面温度的均匀程度。射流速度分别为40、60和80 m/s时，对应的表面最大温差（DT）分别为257.9、267.5和236.8 K。因此，空气射流速度为80 m/s时，玻璃表面温度均匀性最佳，有

图7 t ＝11 s时，不同射流速度下的瞬态温度分布

3.2 喷孔到玻璃距离

喷嘴到玻璃的距离不同，气流在玻璃表面的对流传热量也存在差别。在本研究中，设置喷孔到玻璃的距离分别为16、24和32 mm，即H/D分别为4、6和8。玻璃表面平均温度以及玻璃中心点和表面中心点温差的变化规律见图8。

由图8可以看出，随H/D的减小，玻璃的冷却速率和温差均升高，且最大温差出现的时刻提前。这是因为H/D越小，玻璃近壁面处流体速度越大，表面传热越强，有利于玻璃的钢化，但该影响并不是很明显。

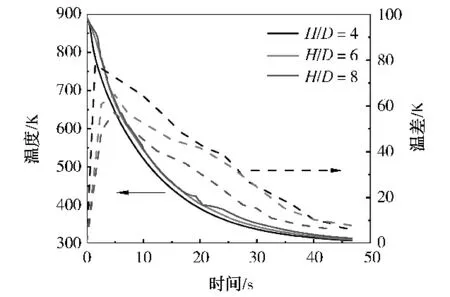
图8 玻璃表面平均温度以及玻璃中心点和表面中心点温差的变化规律

图9为t＝11 s时，玻璃表面温度云图分布。H/D＝4、6和8时的表面最大温差（DT）分别为236.8、284和177.9 K。因此，H/D＝8时，温度均匀性越好。但在实际生产过程中，一般不宜调节风栅高度来改变玻璃的降温速率，因此要确定一个最佳的喷气距离，使玻璃快速而均匀的冷却。

图9 t ＝11 s时，不同射流速度下的瞬态温度分布

3.3 喷孔间距

在本研究中，设置喷孔间距为16、24和32，即S/D分别为4、6和8。玻璃表面平均温度以及玻璃中心点和表面中心点温差的变化规律见图10。

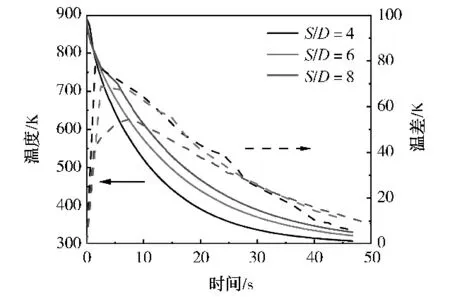
图10 玻璃表面平均温度以及玻璃中心点和表面中心点温差的变化规律

由图10可以看出，随S/D的增大，玻璃冷却速度降低，玻璃厚度方向上的温差减小并且最大温差值出现的时间点逐渐延迟，不利于玻璃的钢化。这是由于S/D越大，喷孔的数量越小，作用到玻璃表面冷气的质量流量越低，传热量降低。

图11为t＝11 s时，玻璃表面温度云图分布。可以看出在不同S/D条件下，玻璃表面的温度分布趋势也不同，这是因为不同的间距会影响玻璃表面流场的分布，冲击玻璃表面的流动模式受喷孔排布的影响。此外，玻璃表面的最高温度区域的温度值以及面积都随着S/D的降低而减小。这代表玻璃表面上的温度梯度变小，换热更加均匀。S/D＝4、6和8时，玻璃表面最大温差（DT）分 别 为236.8、312.7和285.4 K，也证明了S/D＝4时温度均匀性最好。

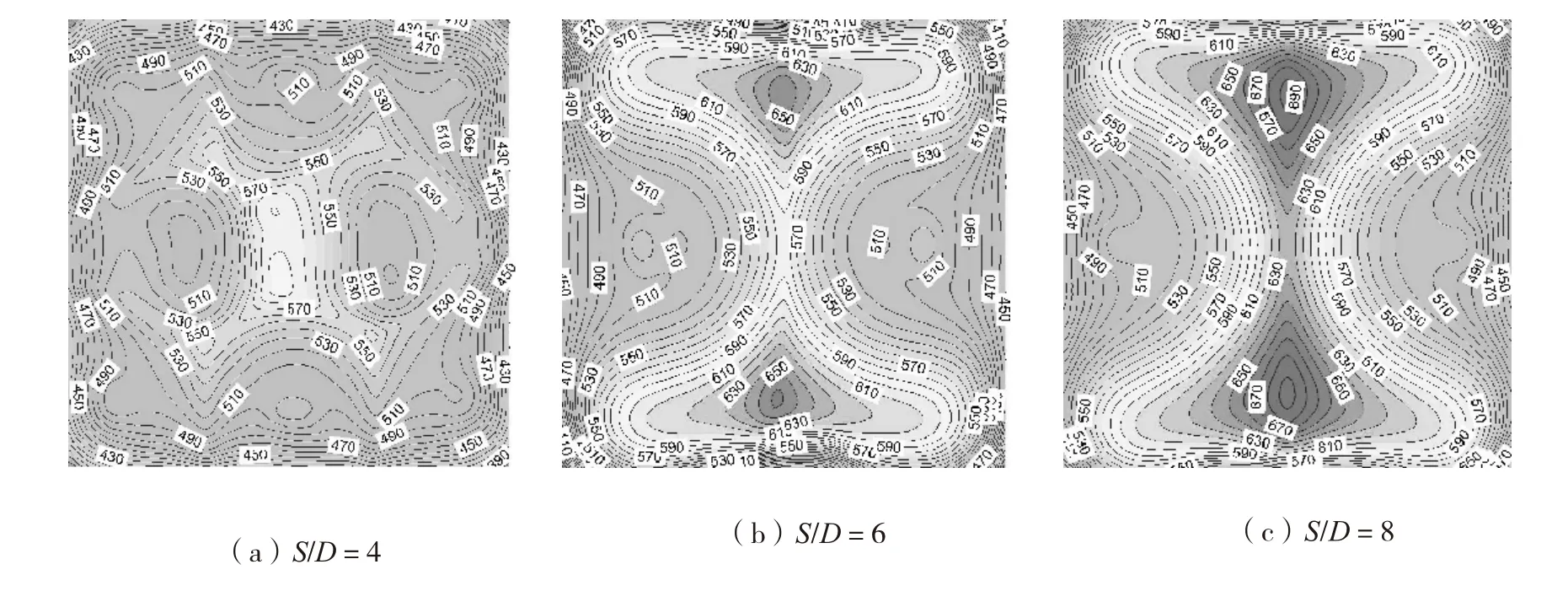
图11 t ＝11 s时，不同S/D条件下的瞬态温度分布

3.4 排布方式

在本研究中 设置排布方式分别为等边三角形、正方形和菱形 如图12所示。图13 a 为不同排布方式下玻璃表面传热系数变化 图13 b为不同排布方式下玻璃中平面与玻璃表面平均温度差值的历史变化。

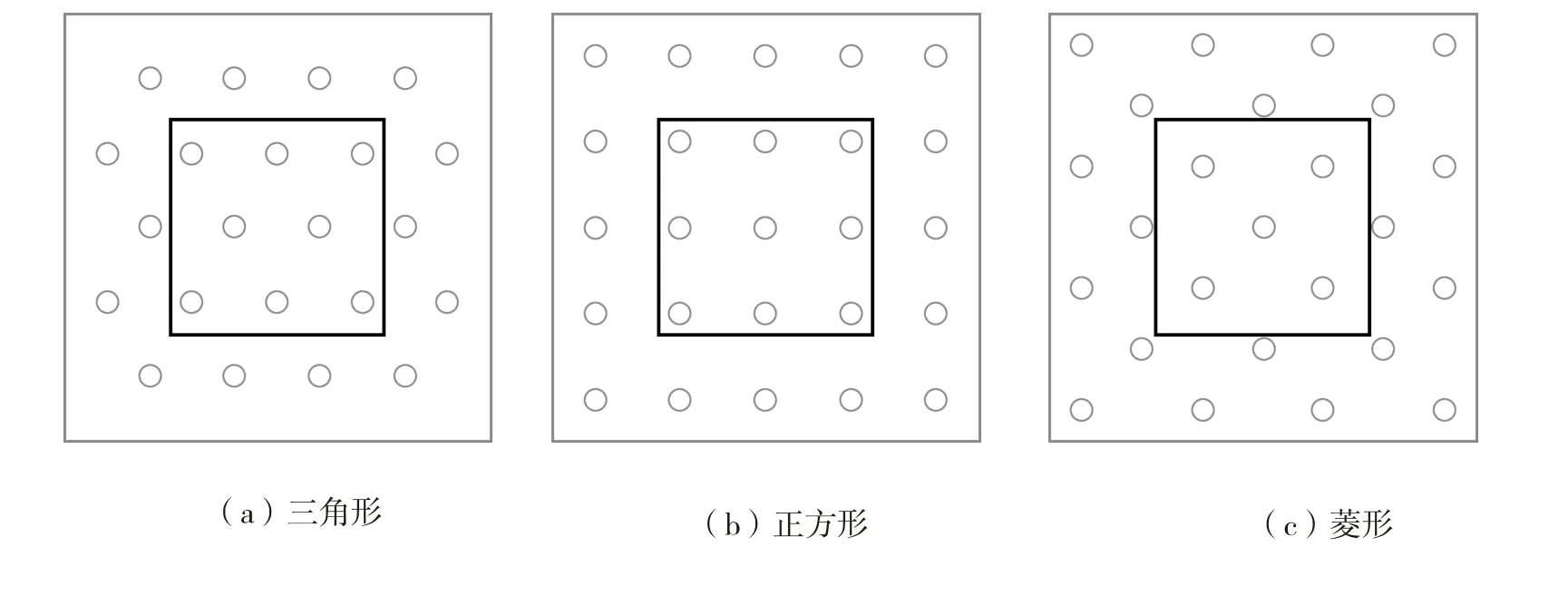
图12 喷孔排布示意图

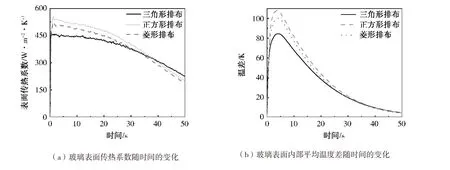
图13 传热系数及温度变化示意图

由图13（b）可以看出，正方形排布方式下玻璃表面和内部的温差最大，其次是菱形排布，最次是三角形排布。这是由于模型中正对玻璃的喷口数量对于三角形排布、正方形排布和菱形排布来说分别为8个、9个和5个，因此喷孔数最多的正方形排布方式下的平均表面换热系数最高，如图13（a）所示。

图14为t＝11 s时玻璃表面温度云图分布。三角形、正方形和菱形喷孔排布下表面最大温差（DT）分别为227、261和252 K，即三角形排布方式下表面温度均匀性最好，其次是菱形，最次是正方形 这是因为不同的喷孔排布影响玻璃表面流场的分布。由于三角形排布下玻璃表面形成的压应力值最小 因此在选择喷孔排布时应针对应力值和应力分布均匀性两方面综合考虑。

图14 t＝11 s时不同排布方式下玻璃表层截面温度云图

4 结论

本文对玻璃喷气钢化过程进行了仿真模拟，研究了玻璃在喷气淬冷钢化过程中的传热特性；并分析了射流速度、喷孔到玻璃的距离、喷孔间距、喷孔排列方式对玻璃的冷却速率及温度均匀性的影响规律。得出以下结论：

（1）在喷气冷却过程中，玻璃表面的温度是不均匀的，玻璃的边缘区域和玻璃的四个角处的温度是最低的，其次是喷孔射流冲击的滞止区。

（2）随射流速度的增加，玻璃的冷却速率和内外温差均增大。此外，在本研究范围内，射流速度为80 m/s时，玻璃表面温度均匀性最佳，有利于玻璃钢化。

（3）喷孔到玻璃的距离越小，玻璃表面传热效果越好，即H/D＝4时取得最大应力值，但玻璃表面温度均匀性最佳值在H/D＝8时取得。

（4）随喷孔间距的减小，玻璃内外温差增高，所选喷孔间距中换热性能最好的是S/D＝4。并且，S/D＝4时温度均匀性最好。

（5）通过分析喷孔排布对传热性能的影响，得出正方形排布可以在玻璃中形成更大应力，但菱形排布有更均匀的换热效果，因此在选择喷孔排布时应综合考虑。