支撑物对钢化真空玻璃传热影响的研究

2022-08-10管长征胡东方

节能技术 2022年3期

管长征，胡东方

(河南科技大学机电工程学院，河南洛阳 471003)

0 引言

随着节能降耗的呼声不断高涨，钢化真空玻璃一经问世，其结构和性能就受到了广泛的关注[1-2]。钢化真空玻璃作为新生的节能玻璃产品，具备隔声降噪、节能降耗、保温隔热等特质，更兼备高强度、抗冲击等安全性能优势，广泛应用于建筑、农业、交通以及光伏建筑一体化等领域[3-4]。

钢化真空玻璃由两块钢化玻璃构成，玻璃间用微小支撑物隔开，周边用封接材料封接[5-6]。支撑物作为钢化真空玻璃的重要组成部件之一，它的设计对钢化真空玻璃的传热性能有着重要的影响[7-10]。在钢化真空玻璃的研究中，许威[11]研究了影响真空玻璃传热系数的主要因素，得出了Low-E玻璃辐射热导和支撑物热导为影响真空玻璃传热系数的主要因素；张亮等[12]研究了真空玻璃的保温性能；张凡等[13]得出了适当调整支撑物的尺寸和间距，可以在保证力学性能的基础上，使得玻璃同时具有低的热导；赵洪凯等[14]分析了支撑物截面形状和固定装置与支撑物性能间的关系，改善了真空玻璃的传热问题；赵伟同[15]利用灰色系统理论得到了支撑物参数与玻璃导热系数的灰关联值；赵骁真[16]运用灰色关联理论研究了钢化真空玻璃各个指标对其传热系数的影响;1913年卓勒在其专利首次提出了真空玻璃的概念之后，从20世纪80年代起，世界对真空玻璃的研发逐渐活跃起来[17];美国Guardian公司为代表的研发企业围绕局部加热、激光加热、红外特征吸收封接等方式申请了多项专利，并制备出实验室样块[18]。然而，国内外大多数学者对钢化真空玻璃强度的研究很多，大多关注钢化真空玻璃安全性的研究，却很少有学者对钢化真空玻璃传热进行分析，忽略了钢化真空玻璃对于建筑能耗的影响。

本文针对钢化真空玻璃的传热机理，主要分析支撑物对玻璃的传热影响，通过建立钢化真空玻璃的传热模型，进行有限元仿真，对不同的支撑物参数模型进行数值模拟分析，得到了钢化真空玻璃传热中心区域的最大热通量。

1 钢化真空玻璃的传热机理分析

1.1 钢化真空玻璃的结构组成

钢化真空玻璃的结构由两片钢化玻璃、封接材料、微型支撑物、钢化玻璃内侧阻挡紫外线的Low-E薄膜以及吸气剂组成，微型支撑物将两片玻璃隔开，微型支撑物的作用避免两片钢化玻璃在大气压的作用下造成挤压变形，导致钢化真空玻璃的性能受损，其中一片钢化玻璃内侧制备一吸气剂槽，放置吸气剂，保证钢化真空玻璃内部有良好的真空度，另一片钢化玻璃上面制备一抽气孔，两片钢化玻璃四周用封接材料进行气密封接。钢化真空玻璃的结构示意图如图1所示。

图1 钢化真空玻璃结构示意图

1.2 钢化真空玻璃的传热机理

当钢化真空玻璃的两侧存在温度差异时，热量会从温度较高的一侧传递到温度较低的一侧，在热量传递的过程中，有两片玻璃板内表面的热辐射，封接材料区域也在进行热量的传递，还有支撑物以及残余气体都可以进行热传导，这些热量传递的物理过程是同步进行的。因此，钢化真空玻璃中心区域的传热方式主要有辐射传热、残余气体传热和支撑物传热。钢化真空玻璃中心区域的传热机理示意图如图2所示。

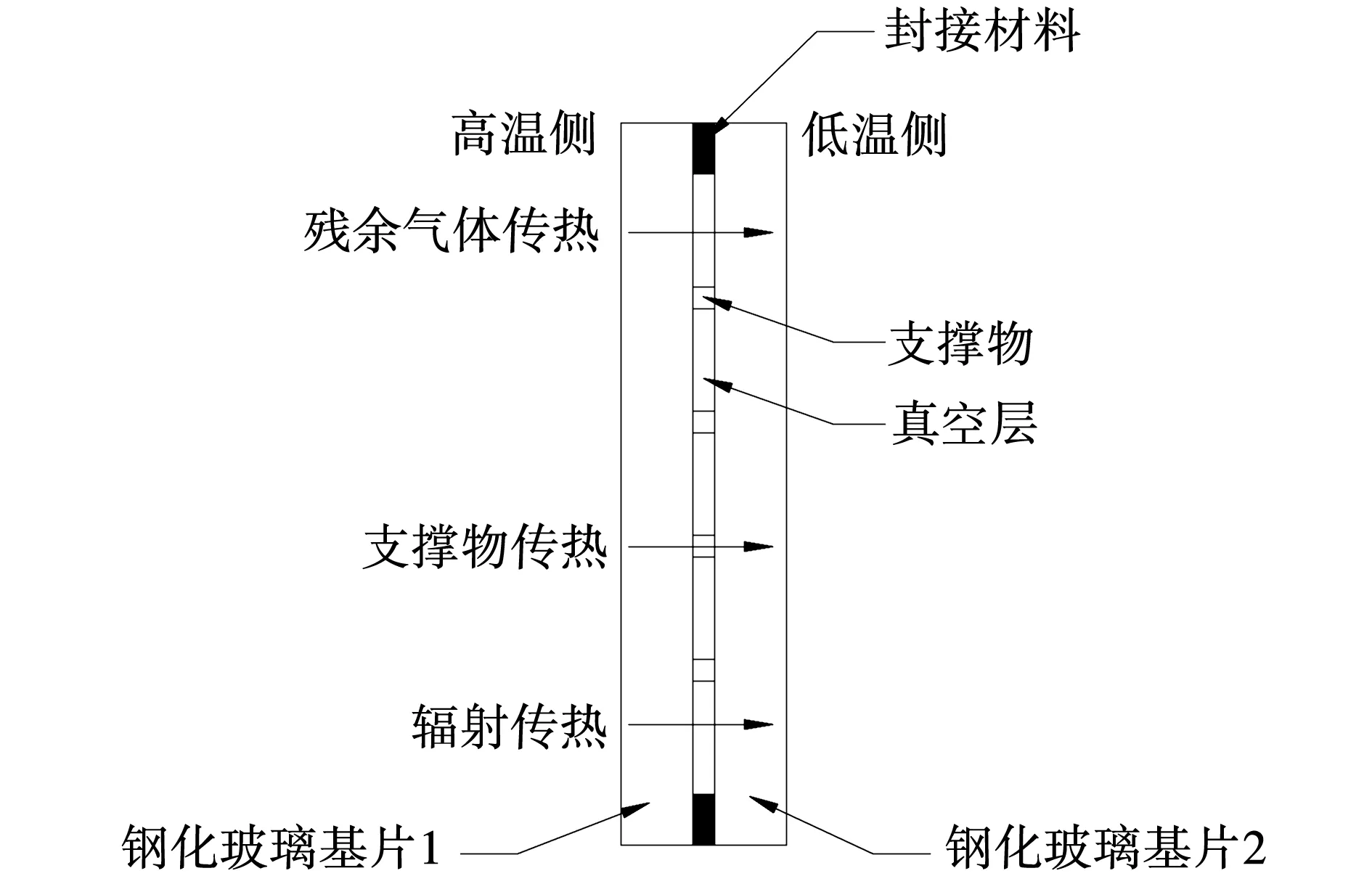
图2 钢化真空玻璃中心区域的传热机理示意图

2 支撑物对钢化真空玻璃传热系数的影响

在钢化真空玻璃中心区域的传热方式中，由于Low-E薄膜的作用，有效地阻挡了热辐射，减少了热量的传递，故辐射传热对钢化真空玻璃中心区域的传热影响很小。当钢化真空玻璃真空层内的压强小于10-2Pa时，残余气体的传热可以忽略不计。因此，支撑物的热传导是钢化真空玻璃中心区域传热的主要影响因素。

为了增加整体玻璃的美感，必须保证钢化真空玻璃内的支撑物足够小，在支撑物足够小的情况下，也要满足其使用性能，当钢化真空玻璃在明视距离0.25 m外，对于人眼张角的角度小于0.1度时，此时，人眼是无法分辨出来的。由于支撑物与两片钢化玻璃直接接触，当支撑物的尺寸越小时，其与钢化玻璃的接触面积就越小，钢化真空玻璃的热导也就越小，式(1)[19]为支撑物的热导率计算公式

(1)

式中U玻——玻璃的导热系数/W·(m·K)-1，约为1 W/(m·K)；

r——支撑物与玻璃接触区域半径/m；

d——支撑物布放间距/m；

h——支撑物的高度/m；

U支撑物——支撑物材料导热系数/W·(m·K)-1。

支撑物的形状常见的有球形、圆柱形以及圆环形等，由于支撑物的形状不同，支撑物对玻璃的传热影响也不同，球形支撑物与钢化玻璃的接触为点，大大减小了接触面积，但球形支撑物使得玻璃受力更集中，易造成玻璃产生裂纹，圆柱形和圆环形为面接触，相对来说，不易产生裂纹，但会使得传热量更多。支撑物的材料选择有很多，如有机非金属、玻璃、金属、陶瓷等，材料的热导率越低，支撑物的热导越低，同时，支撑物材料也要满足一定抗压能力，支撑物在钢化真空玻璃中起支撑作用，承受一定的压力，所以，支撑物材料也要满足强度要求。

在钢化玻璃上布放支撑物时，需要设计相邻支撑物的间距，同时支撑物的布放还要遵循一定的规律，可以避免钢化真空玻璃受力不均产生变形。支撑物的布放间距越大，支撑物在钢化真空玻璃中的布放数量就越少，传热能力也就越低，但在考虑传热问题的同时，也要注意支撑物的受力问题，支撑物的数量能够影响传热，也要考虑受力问题。同样，支撑物的排布方式也会影响支撑物的数量，常见的支撑物的排布方式有正方形排布、正三角形排布和正六边形排布，支撑物的三种排布方式示意图如图3所示。

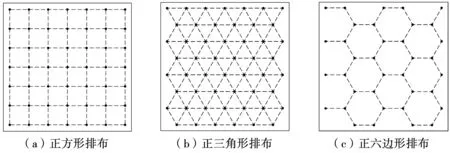
图3 支撑物的三种排布方式示意图

3 支撑物对钢化真空玻璃传热的数值模拟分析

有限元分析是一种数学模拟方法，利用数学近似的方法对真实物理系统进行模拟，把复杂问题简单化，它可以用来求解物体的传热问题。根据JC/T 1079-2008《真空玻璃》标准，钢化真空玻璃的中心区域作为传热测量的有效部分。因此，为了提高钢化真空玻璃的保温隔热性能，针对支撑物的尺寸、形状、材料、布放间以及排布方式进行分析，通过上面的理论分析以及部分学者的研究得出，支撑物的形状、尺寸以及材料对钢化真空玻璃的传热影响较小，而支撑物的布放间距和排列方式对玻璃的影响较大，下面通过有限元数值模拟软件主要对支撑物的布放间距和排列方式进行传热分析。

3.1 参数的设定

钢化真空玻璃的实体模型较大，在进行仿真时，计算量过大，求解效率低，由于钢化真空玻璃本身结构对称性强，结构比较规则，因此，为了提高数值仿真效率，对模型进行简化，钢化真空玻璃的参数设定如表1所示。

表1 钢化真空玻璃各参数

由于钢化真空玻璃的中心区域作为传热测量的有效部分，在进行数值模拟时，取钢化真空玻璃传热模型的一部分，以钢化真空玻璃中心区域的一个支撑物为单元，支撑物三种排列方式的中心单元几何模型如图4所示。

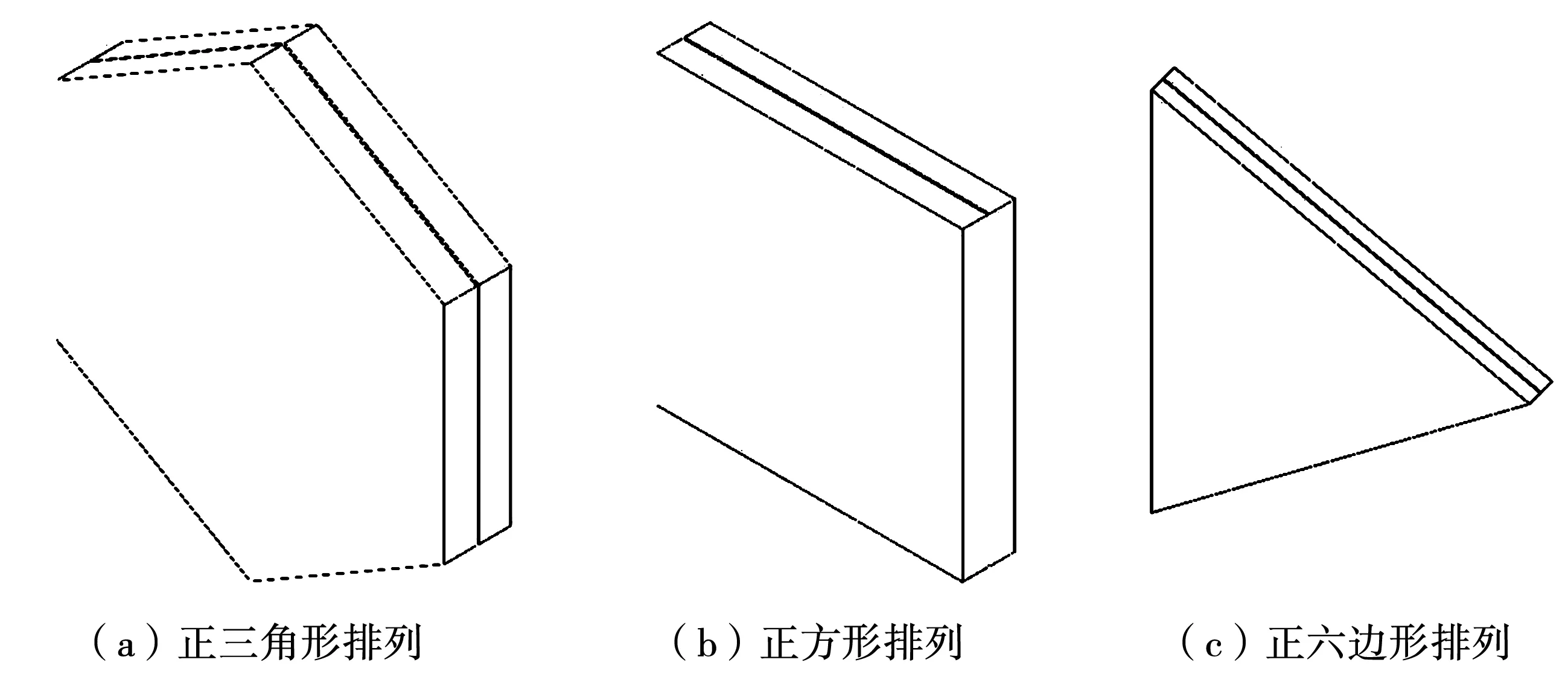
图4 支撑物三种排列方式的中心单元几何模型

钢化玻璃基片是由白玻璃经过热处理得到，封接材料由Cerasolser CS186合金制成，支撑物的材料选择304不锈钢，查询相关资料，得到钢化真空玻璃各个组成部分的热导率如表2所示。

表2 钢化真空玻璃各材料的热导率

钢化真空玻璃在进行有限元模拟仿真时，需要对钢化真空玻璃模型进行边界条件的设定，钢化真空玻璃在实际应用过程中，其四周侧面是嵌入玻璃边框中，结构对称，设置钢化真空玻璃四周侧面为绝热边界条件，根据国家标准GB/T 8484-2008建筑外门窗保温性能分级及检测方法标准和JGJ_T 151-2008建筑门窗玻璃幕墙热工计算规程进行设定。以冬季为例，假设室内温度为18 ℃，室外温度为-20 ℃，边界条件的设定如表3所示。

表3 钢化真空玻璃数值模拟边界条件

4.2 数值模拟结果与分析

数值模拟时，分别对支撑物的布放间距和排列方式进行仿真分析。在支撑物的布放间距仿真时，支撑物选择球形，直径为0.3 mm，排列方式正方形排布，布放间距分别为40 mm、50 mm、60 mm，分别对不同布放间距的钢化真空玻璃设定边界条件，施加热源，得到钢化真空玻璃中心区域的最大热通量云图，钢化真空玻璃的其他结构被隐藏，支撑物云图如图5所示。

图5 支撑物不同布放间距下钢化真空玻璃中心区域的热通量

由图4可知，布放间距为40 mm、50 mm、60 mm钢化真空玻璃中心区域的最大热通量分别1.423 4 W/mm2、1.402 4 W/mm2、1.382 6 W/mm2。从得到的结果可以看出：布放间距从40 mm到60 mm，最大热通量降低了约3%，故支撑物的布放间距对钢化真空玻璃的影响较大。

同样，对三种支撑物的排列方式进行仿真分析，支撑物选取球形，直径为0.3 mm，布放间距为60 mm。分别对不同支撑物排列方式的钢化真空玻璃设定边界条件，施加热源，得到钢化真空玻璃中心区域的最大热通量云图，钢化真空玻璃的其他结构被隐藏，支撑物云图如图6所示。

图6 支撑物不同排列方式钢化真空玻璃中心区域的热通量

由图5可知，排列方式为正三角形、正方形、正六边形钢化真空玻璃中心区域的最大热通量分别为2.095 7 W/m2、1.382 6 W/m2、1.591 4 W/m2。从得到的结果可以看出：从正三角形到正方形，最大热通量降低了约34%，支撑物的排布方式对钢化真空玻璃的影响较大，所以采用支撑物正方形排布的钢化真空玻璃隔热保温性能更好。

在钢化真空玻璃的实际生产制造过程中，上述仿真结果对选择优化钢化真空玻璃传热模型具有实用性，能够有效降低玻璃能源的消耗，对国家呼吁的绿色节能理念具有重要的现实意义。