Model Predictive Control Based Defensive Guidance Law in Three-Body Engagement

Jinglei Ren, Zhenya Wang, Feng Fang

Abstract: Model predictive control (MPC) has been widely used in process industry, but its applications to missile guidance law are relatively rare. In this paper, MPC is introduced to design defensive guidance law in a three-body engagement, where a defending missile (i.e., defender) is employed to protect a target aircraft from an attacking missile. Based on nonlinear kinematic equations, an explicit linear discrete-time model is derived as the predictive model. Then the defensive guidance problem is formulated as a quadratic programming problem, and a fast algorithm for the MPC guidance law is developed. The advantages of the MPC guidance law include the applicability to scenarios with unknown guidance strategy of attacking missile, nonlinear kinematics and multiple constraints. Another key feature is that the proposed approach does not require alteration in the target maneuver. Simulation results show that the MPC guidance law works well and can meet real-time requirements.

Keywords: defensive guidance law; model predictive control; three-body engagement

1 Introduction

Model predictive control (MPC) also known as receding horizon control, is a control framework that can simultaneously handle constraints, optimize performance and provide robustness in a systematic and elegant approach, via repetitive online optimization [1-2]. MPC has been widely used in process industry, power electronics,robots and so on, including systems with complex dynamics, long delay times or unstable system[3]. However, there are few applications of MPC to the field of missile guidance law. In [4-5],the predictive missile guidance laws were presented in the framework of probability density function, which aimed to maximize the probability of successful interception. However, high computation costs are resulted, in order to obtain the optimal control action at each time. This is an important motivation for the present work.

In traditional one-on-one engagement, it is difficult for an aerial aircraft (i.e., target) to evade an attacking missile equipped with modern guidance laws. To protect the target, a defending missile (i.e., defender), which is launched by the target or a friendly platform, is employed to impact the attacking missile. Thus,the target, defender and attacking missile constitute the three-body engagement, which includes two engagements of missile-target and defendermissile. The main approaches to investigate the three-body engagement include optimal control[6-10], differential game[11-13] and sliding model control [14-15]. However, in [6-10] the authors built the linear kinematic model under some linearity assumptions, and additionally assumed the guidance strategy of attacking missile is known.In [12-13], the authors assumed the control/acceleration limit is known. However, in practical application, prior information of enemy missile(i.e., attacking missile), including guidance strategy and control bounds, is unavailable, while, the linearity assumptions may be invalid in some scenarios.

To deal with this situation, the MPC technique is employed for the three-body engagement. A general linearization approach that combines Taylor expansion technique and the transition matrix, is proposed to transform the nonlinear kinematic model into an approximate linear discrete-time model. By using the linear discretetime model as the predictive model, the defensive guidance problem becomes a quadratic programming problem, in which we aim to minimize the objective function containing the quadratic terms of line-of-sight (LOS) angular velocity and relative distance, with bounded control constraints. Then by solving this quadratic programming problem, a fast MPC guidance algorithm is proposed.

The main contributions of this paper are summarized as follows. 1) As far as we know,MPC is firstly applied to three-body engagement.Compared with the work in [6-13], with the help of MPC framework, the proposed approach has the advantage of easy incorporation of additional constraints without changing the control design scheme. 2) Different from the guidance laws in [6-10], the MPC guidance law has the ability to deal with a wide range of scenarios,including unknown information of attacking missile and nonlinear kinematics. 3) Compared with the predictive guidance in [4-5], the MPC guidance here is easily implemented, and it can satisfy real-time requirements.

The paper is organized as follows. In Section 2, the three-body engagement is introduced and the defensive guidance problem is formulated as a nonlinear MPC problem. In Section 3,the general linearization approach for transforming a nonlinear continuous system into an approximate linear discrete-time system is proposed, and the effectiveness of the approach is verified via simulations. Then, in Section 4, the defensive MPC guidance law is developed. The performance of the MPC guidance law is analyzed in Section 5, and conclusions are provided in Section 6.

The agents in the three-body engagement are defined as follows: a target aircraft denoted as T,a defending missile denoted as D and an attacking missile denoted as M. The attacking missile employs the fixed pursuit guidance law to intercept the target, but it is unknown to defendertarget team. In order to protect the target aircraft, a defender launched by the target or target friendly platform is used to impact the attacking missile. The three-body engagement is divided into two one-on-one engagements:defender-missile (D-M) engagement and missiletarget (M-T) engagement. The geometry of three-body engagement is shown in Fig. 1, whereVi,aiandγirepresent the velocity, acceleration and flight-path angle of each aircraft,λMT, λMDandrMT, rMDare the LOS angles and relative distances of M-T and D-M engagements.

There are three assumptions in this paper.1) The speed of each aircraft is constant.2) Each aircraft flight control system is a firstorder dynamics system, and the relation of aircraft acceleration and guidance command is

2 Problem Statement

Fig. 1 Geometry of three-body engagement

whereuiis guidance command andτiis the time constant. 3) The defender’s guidance command satisfies |uD|≤uD,max, whereuD,maxis the guidance command limit.

In the M-T engagement, an attacking missile uses a fixed pursuit guidance law to pursue the target, such as proportional navigation (PN),augmented proportional navigation (APN),beam rider guidance (BRG) and so on. For example, the pursuit guidance commands of PN,APN and BRG described in [16] are

The defensive guidance problem can be formulated as a nonlinear MPC problem by using Eq.(6) as the predictive model. However, it is hard to obtain the accurate expression of Eq.(6), since it needs to solve the nonlinear differential equations shown in Eq.(4). Additionally, the nonlinear MPC problem is difficult to solve with high computation cost. Thus, we need to find an approximate explicit discrete-time model used for the predictive model, and reformulate the MPC problem as a simple one.

3 Discrete-Time Predictive Model

3.1 General Approach for Linearization and Discretization

3.2 Performance of Discrete-Time Predictive Model

Here, we define three models as follows. M1 is the original continuous nonlinear model shown in Eq. (5), and M2 and M3 are the discrete-time models shown in Eq. (10) and Eq. (15), respectively. M2 or M3 will be used as the predictive model, and the calculation error between the predictive model and the original nonlinear kinematic model determines the performance of MPC. Four factors will influence the calculation error, which are the sampling timeT, the number of stepsN, the initial stateX0and the guidance commands{uD(k)}. The prediction horizon is equal toNT. IfNTis chosen too large, then the results of predictive model will deviate from the original nonlinear kinematic model significantly. This is because the predictive model is linearized around the initial stateX0, and as the number of steps increases, there will be large model errors, which will lead to large errors in results. After several simulations with differentNandT, the following suggestion is given: if we chooseNT≤1.5 s andT≤0.1 s, both the linearized discrete-time models M2 and M3 match the actual model M1 well.

Then in the condition ofT=0.05 s andN=10, we test the performance of M2 and M3 in various initial states and guidance commands,which are obtained from a successful defensive engagement. Here, for illustrating the problem,two cases are selected: the first case has a horizon from 2.85 s to 3.35 s, of which the initial relative distance is 4886.4 m far away from zero;and the second case is at the end-stage having the horizon from 6.8 s to 7.3 s, of which the initial relative distance is 539.2 m going close to zero. The simulation results are shown in Figs. 2-3, where Error 12, Error 13 and Error 23 refer to the absolute result errors between M1 and M2,M1 and M3, and M2 and M3, respectively. In Fig. 2, it is seen that the absolute errors are small and acceptable in the first case, which demonstrates that the performances of M2 and M3 are close to that of M1. In Fig. 3, Error 12 and Error 13 ofλ˙MDsuddenly increased to 0.24 rad/sat the 10th sample time in the second case, due to the accuracy decrease of linearized models.

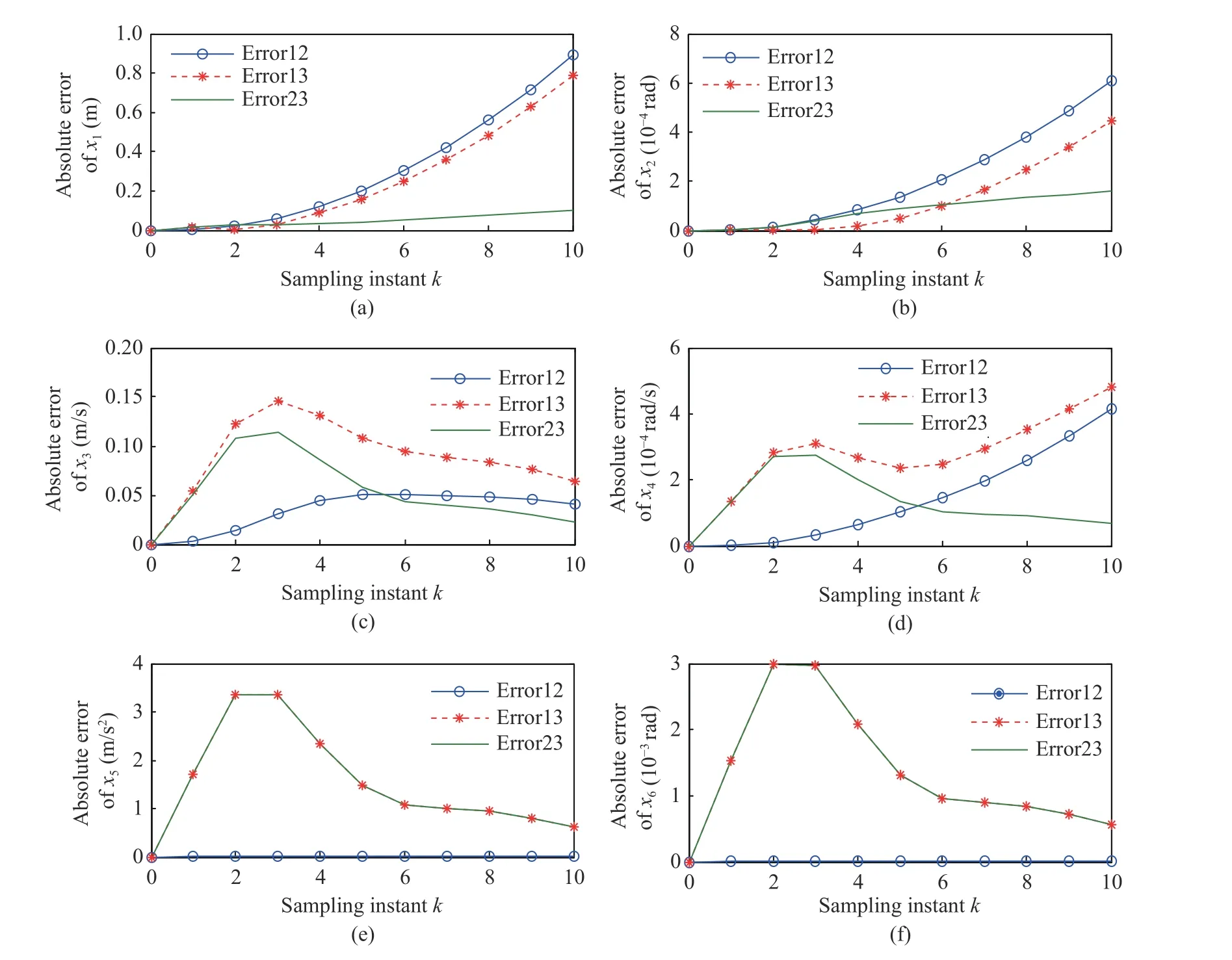
Fig. 2 The absolute errors in the first case: (a)relative distance; (b)LOS angle; (c)closing velocity; (d)LOS angle rate; (e)acceleration; (f)flight-path-angle

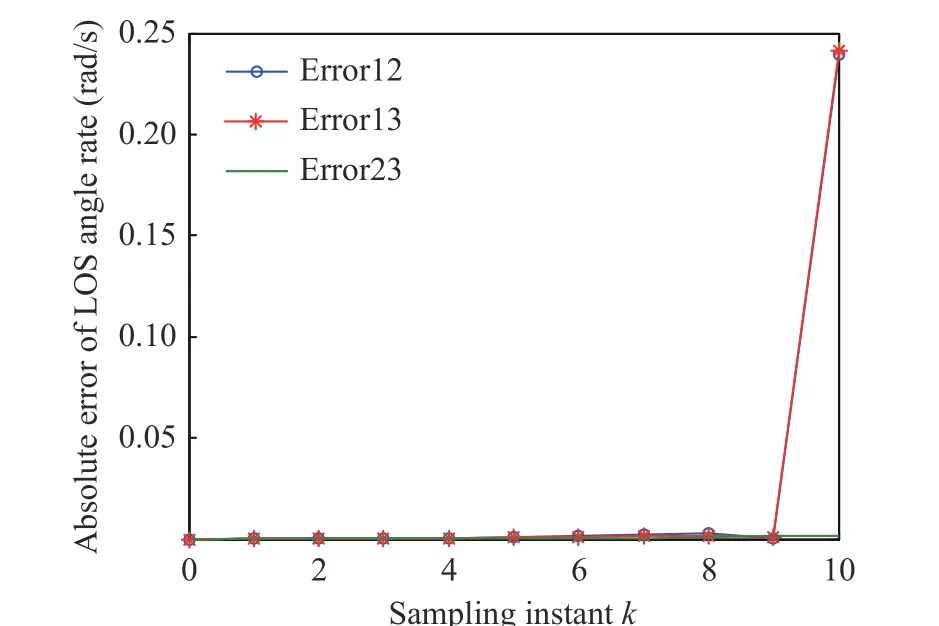
Fig. 3 The absolute errors of D-M LOS angle rate in the second case

Furthermore, we test other situations of different initial states and guidance commands,except for the above second case at the end-stage of engagement, and all the results show that both M2 and M3 perform closely to M1. The performance deterioration at that end-stage can be explained as follows. According to Eq. (4), the accuracy of linearized model (i.e., M2 or M3) is particularly influenced by the relative distance(i.e.,x1) as it appears in the denominator. Thus,at the end-stage, as the relative distance goes close to zero, the accuracy of the linearized model decreases substantially. As a consequence, the results of M2 and M3 at the end-stage will deviate from the actual values significantly.

After numerous tests, we conclude that both the M2 and M3 can match the actual nonlinear kinematic model well with the appropriate sampling timeTand number of stepsN. Meanwhile,at the end-stage, we need to decrease the forward stepNfor acquiring the good performance,and it will be discussed in Section 4.

4 Model Predictive Guidance Law

The sufficient condition of successful interception for D-M engagement is described as

wheret1is a time instant satisfyingt1∈(0,tfMD],andtfMDis the D-M interception time. Eq. (16)shows that aftert1, the LOS of D-M engagement remains fixed, and in this situation, as long as the defender and attacking missile keep getting close to each other, the defender will impact the attacking missile. The basic idea of PN and APN tries to satisfy this sufficient condition, i.e., the interceptor (the role played by the attacking missile in this paper) that tries to nullify the interceptor-target LOS rate change when it approaches to its target. Inspired by this idea,the LOS rate of D-M engagement is considered into the objective function. Also, we expect that the defender approaches the attacking missile quickly with acceptable control effort. Thus, the objective function of MPC guidance problem is described as

where blkdiag(·) represents the block matrix.

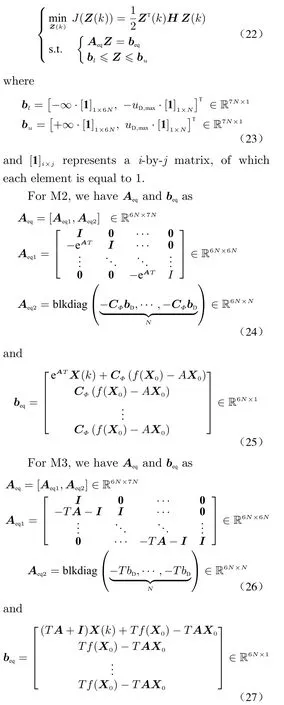
By using M2 and M3 as the predictive models and considering the control input saturation as the inequality constraint, the MPC guidance problem can be formulated as the following quadratic programming problem.To calculate Eqs. (24)-(27), the linearization pointX0needs to be determined. At each time instant, the current stateX(k) is available,which is obtained by defender’s tracking system.Thus, we can setX0=X(k), which means that the M2 and M3 are linearized around the current state.

According to the analysis of Section 3.2,when the defender gets close to the attacking missile, the model errors of M2 and M3 become large if we use the large prediction horizon. Thus,in order to avoid the large model error at the end-stage of D-M engagement, the approach of variable length of prediction horizon is introduced as follows. Calculate the approximate time-to-go of D-M engagement astgo,MD=rMD/|r˙MD|, and compare time-to-go and the length of prediction horizon. Iftgo,MD≥NT, thenNkeeps the original value; however, iftgo,MD＜NT, we setN=floor(tgo,MD/T), where function floor(x) represents getting the nearest integer less than or equal tox.

At each guidance time, the MPC guidance problem in Eq. (22) is solved, of which the optimal control sequence is derived, and the first control action in this sequence is applied as the current guidance command. The MPC guidance scheme is shown in Fig. 4, which includes three steps at each time instant. For step 2, there is a number of commercial software that can be used to solve the quadratic programming problem.Here, the Matlab function “quardprog()” is used to deal with this problem.

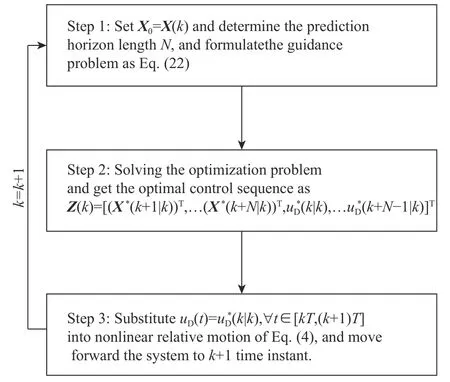
Fig. 4 The MPC guidance scheme

5 Simulation Analysis

Here MPCGL2 and MPCGL3 are defined as the defender’s MPC guidance law based on M2 and M3, respectively. The initial positions of target,defender and attacking missile are (8 000, 0) m,(8 000, 0) m, and (0, 0) m, and the speeds of them are 350 m/s, 450 m/s and 700 m/s, respectively. The initial flight-path angles of target,defender and attacking missile are 25°, 30° and 20°, and the time constants of flight control systems are 0.1 s, 0.4 s and 0.4 s, respectively. The control bound of defender is 20 g. All the simulations are implemented on a laptop with 2.5 GHz Intel i5 CPU.

5.1 Performance of Two MPC Guidance Laws

Here, the performance of MPCGL2 and MPCGL3 is compared. The parameters of two MPC guidance law are set as:N=10,T=0.05 s,α=1 000 andβ=1. The attacking missile uses PN guidance law with navigation ratio asNPN=3, and the target employs zero maneuver.The simulation results are shown in Figs. 5-6,where the defender intercepts the attacking missile before the target is harmed, with either of the MPC guidance laws, with only small differences in guidance commands. The reason for similar performance of both MPC guidance laws is that both M2 and M3 match actual model M1 well in this situation.

The total computation burden of simulation is about 3 s, which is less than simulated flight time (i.e., 7.26 s). The computation time to generate MPC guidance command at each sampling time instant is shown in Fig. 7. Except for the first guidance command with a computation time of about 0.4 s, all guidance commands are obtained in less than 0.05 s (i.e., the sampling period) for MPCGL3. Also, except for the first and second guidance commands, all guidance commands are obtained in less than 0.05 s for MPCGL2. Besides, the computation time of MPCGL3 is less than that of MPCGL2. This is because MPCGL2 has higher computation requirement to calculate the transition matrix by using RK4.

Fig. 5 Flight trajectories in the cases of MPCGL2 and MPCGL3

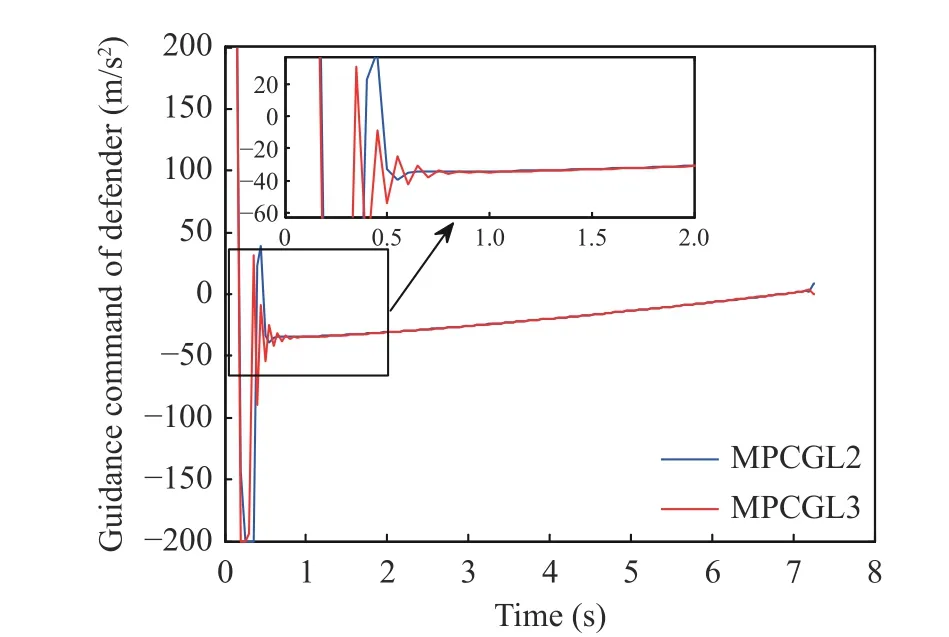
Fig. 6 Defender’s guidance commands in the cases of MPCGL2 and MPCGL3

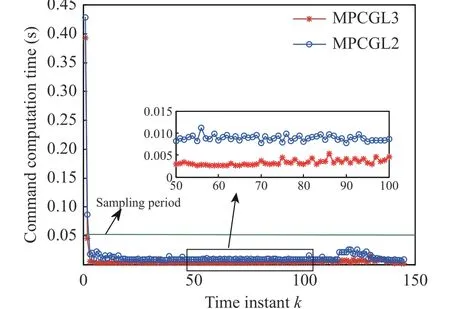
Fig. 7 The computation time for generating guidance command at each sampling time instant

Note that even with a simple laptop without specialized hardware and software, all calculations are easily within the sample time, except at the initial time step(s), where initialization of MATLAB code results in longer computation - a problem that is avoided in actual implementation stage. Thus, by using the proposed MPC guidance laws, the online requirement is easily satisfied in practical applications, since the defender can be equipped with advanced software and high-efficiency optimization algorithms,which can reduce the computation time significantly.

Next, we test the performance of MPC guidance laws with different lengths of prediction horizon. We set sampling time asT=0.05 s and penalty weight asβ=1. In this case, the target employs zero maneuver, and the attacking missile uses PN guidance law withNPN=3. The ranges of effective penalty weightαof MPCGL2 and MPCGL3 are almost same, which are presented in Tab. 1. The resulted D-M miss distances of Tab. 1 are all smaller than 0.05 m,guaranteeing the successful defensive interception. From Tab. 1, it is seen that the MPC guidance law has good robustness for the penalty weight, since the range ofαis large. Also, it is seen that the range ofαincreases as length of prediction horizonNdecreases.

Tab. 1 Range of effective penalty weight with different N

5.2 Special Scenarios

In this subsection, three special scenarios that the references [6-10] cannot handle are discussed.In this section, MPCGL3 is used as the defender’s guidance law, and its parameters are set asN=10,T=0.05 s,α=1 000 andβ=1.

In Scenario 1, the attacking missile uses BRG to purse the attacking missile. Note that BRG does not satisfy the linear forms of guidance laws assumed in [6-10]. The target employs zero maneuver. The beam generator is set at the position of (-8 900, 0) m, which produces a radar or laser beam continuously pointing to the target. The objective of BRG is to fly the attacking missile along a beam. If the beam is always on the target and the attacking missile is always on the beam, then this results in interception. The guidance gain of BRG is set asK=0.1. If there is no defender, the attacking missile with using BRG will intercept the target at 8.020 8 s with M-T miss distance as 0.946 8 m. In this case, the simulation results of MPCGL3 are shown in Fig. 8.It shows that the defender intercepts the attacking missile successfully at 7.34 s with moderate guidance command, and the D-M miss distance is 0.012 m.

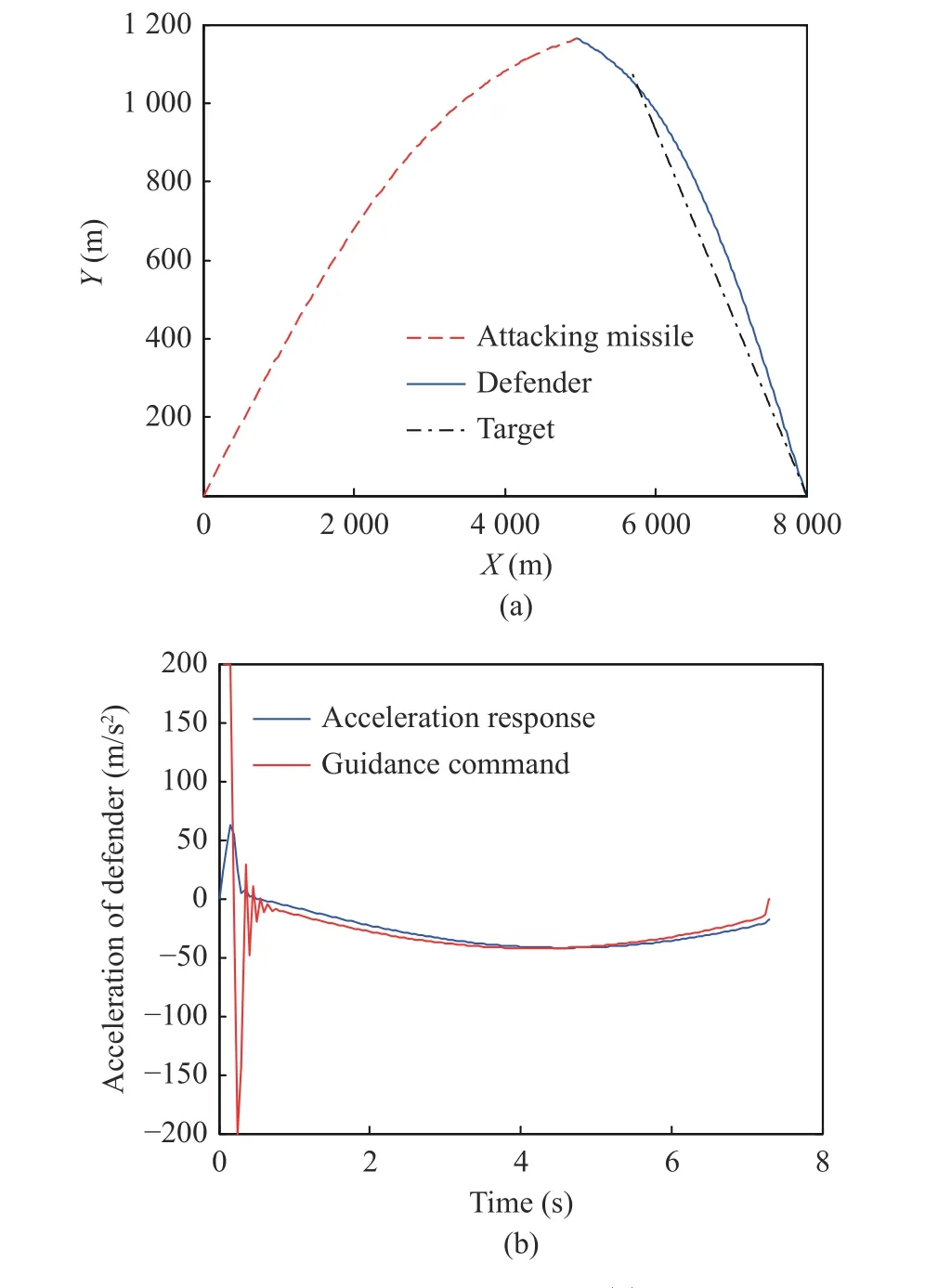
Fig. 8 Simulation results of Scenario 1: (a) flight trajectories;(b) defender’ s guidance command and acceleration response

For comparison, the two-way cooperative guidance law in [7] is adopted in Scenario 1, and the simulation results are shown in Fig. 9. It is seen that the defender misses the attacking missile with miss distance as 36.56 m. Also, the guidance commands grow large quickly at last few seconds. In this case, even with the help of target cooperation maneuver, the defender cannot intercept the attacking missile. The reason for unsuccessful defensive interception is that BRG is inconsistent with the assumption of linear-form guidance law, leading to generating the guidance command error.

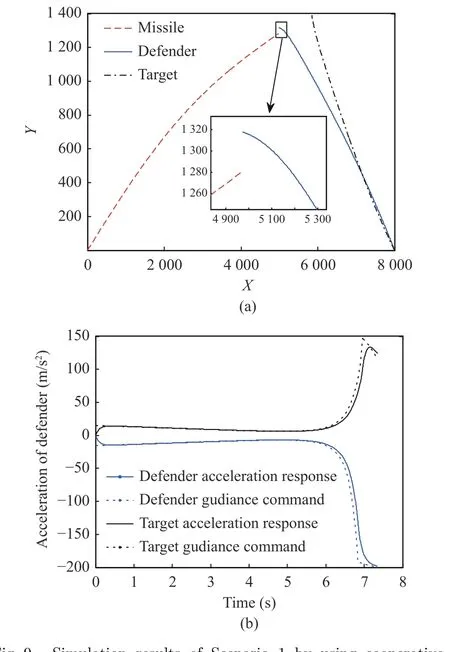
Fig. 9 Simulation results of Scenario 1 by using cooperative guidance law in [7]: (a) flight trajectories; (b) guidance commands of defender and target

In Scenario 2, we consider the large initial LOS angle difference, i.e., |λMT-λMD| which is not small. In this scenario, the linear assumption,that the deviation of D-M and M-T collision triangles is small in [6-10], is not satisfied. Here, we change the initial position and flight-path angle of defender as (4 000, 4 000) m and 90°, respectively. Then, we have |λMT0-λMD0| = 45°. The attacking missile uses PN guidance law with navigation ratio as 3, and the target employs zero maneuver. The simulation results are shown in Fig. 10, which shows the defender intercepts the attacking missile at 6.78 s with appropriate guidance command. As a contrast, the two-way optimal cooperative guidance law in [7] is also used in this scenario, and the cooperative guidance law performs badly. The defender misses the target with miss distance as 56.88 m, and the problem of guidance command oscillation appears. The reason for the above results is that the linearization assumption of small LOS-angle deviation is not satisfied in this scenario.

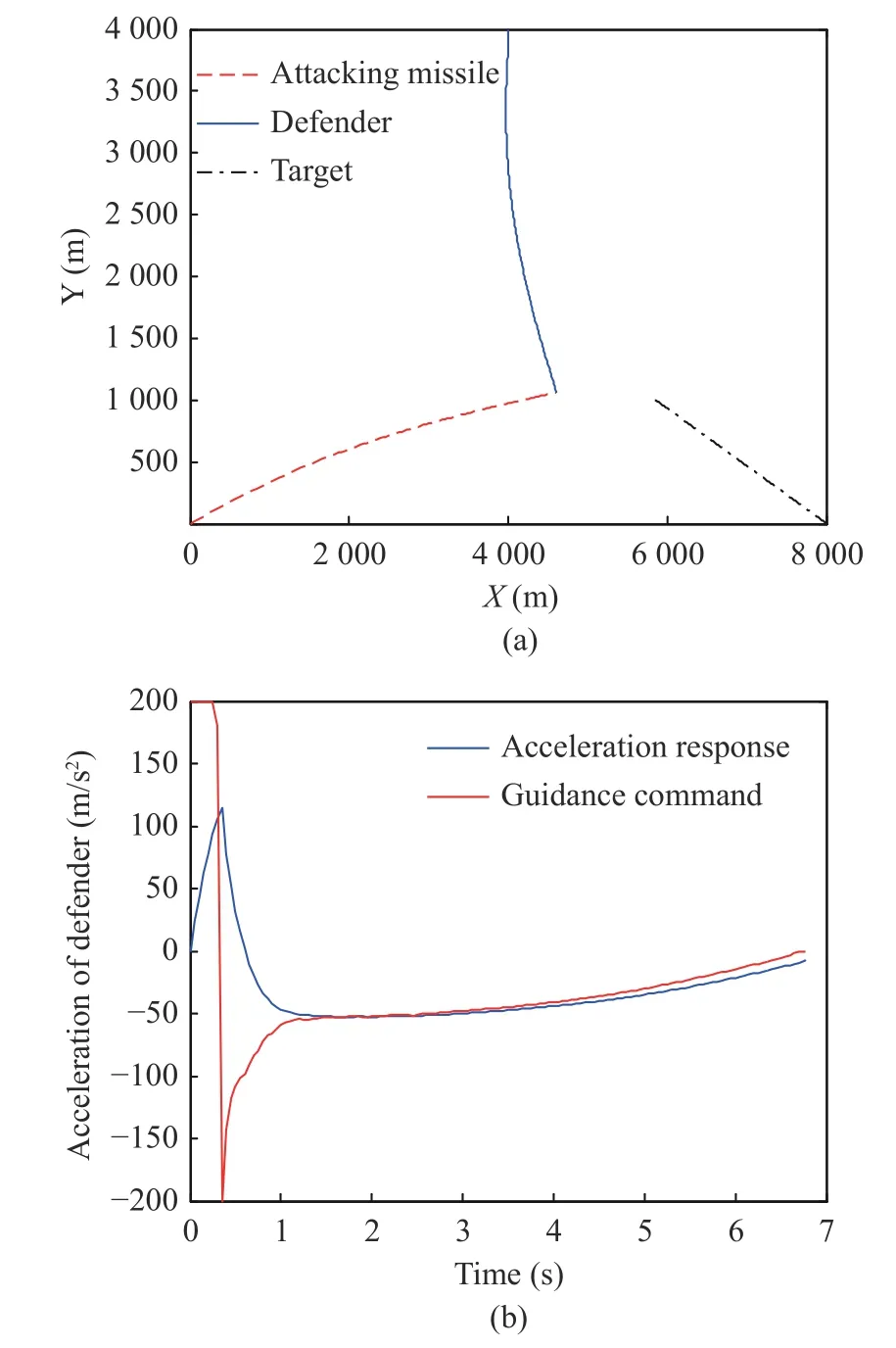
Fig. 10 Simulation results of Scenario 2: (a) flight trajectories;(b) defender’ s guidance command and acceleration response

In Scenario 3, we consider the maneuver of target is unperturbed, which means target can focus on its task without considering the interception of attacking missile. This is different from [6-10], where target needs to employ cooperative maneuver with defender. For example, we assume the unperturbed maneuver of target is constant as 1g. For compensating the target maneuvers, the attacking missile uses APN guidance law with navigation ratio equal to 3. Fig. 11 shows that the defender intercepts the attacking missile at 8.66 s, and the D-M miss distance is 0.01 m. Besides, we test the cases of target using different maneuvers, and the results show that the MPC guidance law has good robustness for attacking missile’s maneuver.

Fig. 11 Simulation results of Scenario 3: (a) flight trajectories; (b) defender’s guidance command and acceleration response

Via the simulation results in this subsection,it is seen that the defensive MPC guidance law has the ability to deal with the scenarios of various pursuit guidance laws and nonlinear kinematics engagement and to allow the target to take its maneuver, unperturbed.

6 Conclusion

In this paper, MPC is applied to design the defensive guidance law in the three-body engagement. The MPC guidance law is a fast algorithm solved as a quadratic programming problem,where the approximate linear discrete-time model is used for the predictive model. The MPC guidance law is guaranteed to work well and satisfy real-time requirements, as shown in extensive numerical simulations. It has good robustness for the unknown attacking missile’s maneuver, and can deal with nonlinear kinematics of three-body engagement. Also, it gives freedom for the target to execute its task.