Distributed Privacy-Preserving Fusion Estimation Using Homomorphic Encryption

Xinhao Yan, Siqin Zhuo, Yancheng Wu, Bo Chen

Abstract: The privacy-preserving problem for distributed fusion estimation scheme is concerned in this paper. When legitimate user wants to obtain consistent information from multiple sensors, it always employs a fusion center (FC) to gather local data and compute distributed fusion estimates(DFEs). Due to the existence of potential eavesdropper, the data exchanged among sensors, FC and user imperatively require privacy preservation. Hence, we propose a distributed confidentiality fusion structure against eavesdropper by using Paillier homomorphic encryption approach. In this case, FC cannot acquire real values of local state estimates, while it only helps calculate encrypted DFEs. Then, the legitimate user can successfully obtain the true values of DFEs according to the encrypted information and secret keys, which is based on the homomorphism of encryption. Finally,an illustrative example is provided to verify the effectiveness of the proposed methods.

Keywords: eavesdropping attack; distributed fusion estimation (DFE); homomorphic encryption;computational privacy

1 Introduction

Recently, many advantages of networks are discovered and used, such as high scalability and low wiring complexity, so networked multi-sensor fusion systems (NMFSs) have received increasing attention [1], and they have been considered in a wide range of applications, including maneuvering target systems [2] and cyber-physical systems [3]. However, due to the gradual openness of NMFSs, they have the risks of suffering network attacks [4], such as denial-of-service attacks [5], replay attacks [6], and eavesdropping attacks [7, 8]. Among various attacks, eavesdropping is a serious kind, since it can not only steal private data, but also make other attacks more menacing. Hence, protecting the information privacy of NMFSs is imperative. Generally, there are two basic data fusion frameworks: the centralized fusion [9, 10] and the distributed fusion[11, 12]. As is known, the distributed fusion structure is more robust and fault-tolerant [13].Thus, we concern about the privacy-preserving methods on distributed fusion estimation.

For countering eavesdropping attacks, there exist plenty of privacy-protecting approaches,such as differential privacy [14], complex noise insertion [8] and homomorphic encryption [15].Homomorphic encryption is an efficient method introduced in [15] that uses a pair of keys and homomorphisms to guarantee computational privacy. The eavesdroppers cannot acquire valid information when the transmission is encrypted with secret keys. Different from complex noise insertion [8], encryption with homomorphic encryption does not consume extra energy. Meanwhile, it will not affect the performance of legitimate user like noise contamination [7] and differential privacy [14]. To be specific, some components of local state estimates are replaced by stochastic noises in [7], while random noises with certain distributions are considered to be added into query in [14]. Although the privacy is guaranteed on certain level, the noises also decrease the system performance. On the contrary, the performance under homomorphic encryption scheme will not be affected, because the required data can be completely decrypted by combining homomorphisms and private keys. Therefore, the homomorphic encryption approach has been embedded for a wide range of studies, such as quadratic optimization [16] and state estimation[17-19]. A secure state estimator was designed with hybrid homomorphic encryption in [17],while the influence of quantization was carefully discussed. Since the performance degradation generated by quantization is slight, we neglect it during the encryption in this paper. Then, by resorting to partially homomorphic encryption,the centralized and distributed fusion Kalman estimators have been studied in [18], but the estimation performance of its distributed fusion is not good enough due to the usage of covariance intersection. Moreover, a secure multi-party dynamic state estimation was proposed in [19].However, the time of each loop is relatively long,because the user needs to broadcast fusion information to all the parties.

According to above analysis, this paper studies the privacy-preserving distributed fusion estimation problem by utilizing homomorphic encryption, since it can achieve high privacy level while does not waste extra energy or damage estimation performance. Besides, the proposed estimation will not establish feedback process,which provides sufficient real-time performance.The main contributions of this paper are summarized as follows. 1) The Paillier homomorphic encryption method is introduced into distributed fusion estimation field to protect the privacy of NMFS. Meanwhile, the fusion criterion weighted by matrix is considered to increase the performance of estimation. 2) Based on certain cryptographic definitions, computational privacy is proved to be guaranteed against semi-honest eavesdroppers.

Consider a NMFS described by the following time-invariant state-space model as

In this paper, we consider the distributed fusion structure owing to its higher robustness and fault-tolerance. The sensors are responsible to calculate local state estimates (LSEs)xˆi(t)based on their sensed variables{yi(1),··· ,yi(t)}.Then, the distributed fusion estimate (DFE)xˆf(t)at each time will be computed by means of weighted sum on LSEs, i.e.

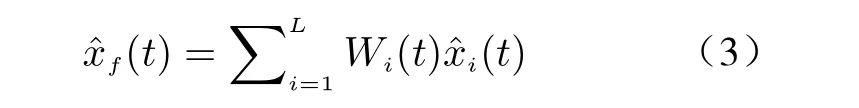
whereW(t)≜[W1(t),W2(t),··· ,WL(t)] is the weighting fusion matrix.

The eavesdropper in this paper is a coalition that colludes with all the sensors and FC by exchanging their information, private cryptographic keys and even the decrypted outputs to infer private data of legitimate user. To prevent information leakage, the Paillier homomorphic encryption approach is considered, where the transmitted data are encrypted with public keys

2 Problem Formulation

for countering eavesdropping, and the data after Paillier encryption are denoted by [[·]]. Under such encryption method, the FC serves as a computation unit, and it can only obtain encrypted fusion estimate [[xˆf(t)]]. Then, after FC calculates and sends encrypted DFEs, the legitimate user can successfully decrypt them to obtain estimatexˆu(t) by using previously generated private key.

Consequently, the main problem to be solved in this paper is to determine the encryption structure to protect the transmission confidentiality of NMFS. Then, all the local information needs to be best utilized for computing an optimal fusion estimate. Finally, the privacy requires being proved by resorting to some concepts about cryptography.

Assumption 1The noisesw(t) andvi(t) are independent and identically distributed (i.i.d.)white Gaussian noises (WGNs) that satisfy

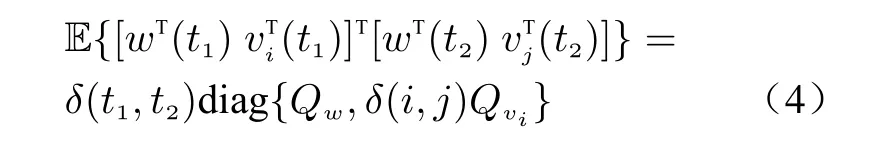
where superscript T represents the transpose,diag stands for a diagonal matrix, E{·}means the mathematical expectation,QwandQvirespectively denote the covariances ofw(t) andvi(t).δ(i,j) is the delta function such thatδ(i,j)=1 ifi=j; otherwise,δ(i,j)=0.

3 Main Results

3.1 Privacy Goals

Before giving main introduction of homomorphic encryption, let us introduce some definitions about cryptographic privacy [20, 21]. First, the eavesdropper is considered to be semi-honest,which is defined as follows.

Definition 1(Semi-honest Model) A party is semi-honest if it does not deviate from the steps of the protocol, but may store the exchanged messages and its internal coin tosses, as well as process the data received in order to learn more information.

Such eavesdropper cannot modify the transmitted data, so the legitimate user can correctly decode with private keys. For countering this kind of eavesdropping, the following privacy target called computational indistinguishability is introduced, where{0,1}*is a sequence of bits with indefinite length andX={Xn}n∈Nis a sequence of random variablesXnthat ranges over strings of bits with a length polynomial inn.

Definition 2(Computational Indistinguishability) The ensemblesX={Xn}n∈NandY={Yn}n∈Nare computationally indistinguishable, denoted asX≡cY, if for every positive probabilistic polynomial-time algorithmD:{0,1}*→{0,1}, every positive polynomialp(·) with all sufficiently largen’s, one has

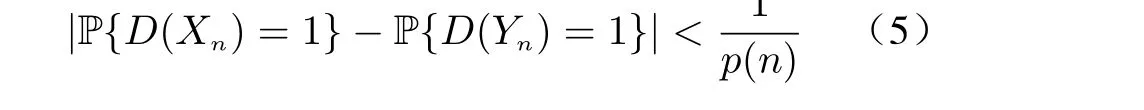
where P means the probability of event.

Then, the execution view requires to be defined.

Definition 3(Execution View) Letf(x¯)=(f1(x¯),f2(x¯),··· ,fL(x¯))be a deterministic polynomial-time function and Π a multi-party protocol that computesf(x¯) with the inputx¯=(x1,x2,··· ,xL). The view of thei-th party during an execution of Π usingx¯ is defined as

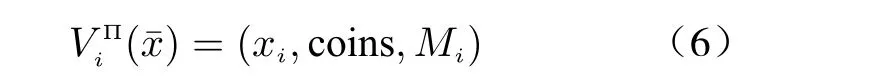
where coins are the outcome of the party’s internal coin toss, andMiis the set of messages it has received. Then, the view of eavesdropperVeΠ(x¯)during an execution of Π is defined as

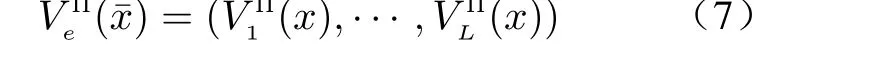
Finally, the multi-party privacy needed to be achieved is defined as follows.

Definition 4(Multi-party Privacy with Respect to(w.r.t.)Semi-honest Behavior) Since the eavesdropper has access to sensors from 1 toL, one hasfe(x¯)=(f1(x¯),··· ,fL(x¯)). We say that the multi-party protocol Π computesf(x) privately if there exists a polynomial time algorithm, denoted by simulatorS, such that

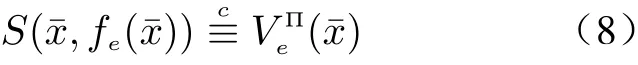
3.2 Homomorphic Encryption

wherer∈ZNis a non-zero random number.

3) Dec(c,sk): Input the private key anda ciphertextc, output the message that was encryptedm. The detailed decrypt process is given as

The Paillier homomorphic encryption provides two fundamental operations: addition and multiplication. They are respectively denoted by“⊕” and “⊗” in this paper, and “⊗” is omitted when the type of multiplication can be inferred.The details of these operations are given as follows.

1) The addition of two values can be described by the following form

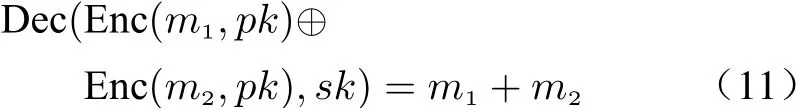
The result can be proved by resorting to the multiplication of encrypted values

Besides, the privacy guarantees of Paillier homomorphic encryption are based on the decisional composite residuosity assumption [22].In distributed fusion structure, LSEs are calculated at sensors with raw measurements. We consider measurements{yi(1),yi(2),··· ,yi(t)}as the basis of estimation at timetinstead of{yi(1),yi(2),··· ,yi(t-1)}, since it provides more information according to projection theory.

To be specific, the standard Kalman filter 23] is adopted to compute each LSE

3.3 Privacy-Preserving Fusion

In practice, the parameters of Kalman filter converge to constant values quickly. Therefore,we assume the Kalman filter has already achieved steady state at start. In this case, the steady-state parameters are defined as

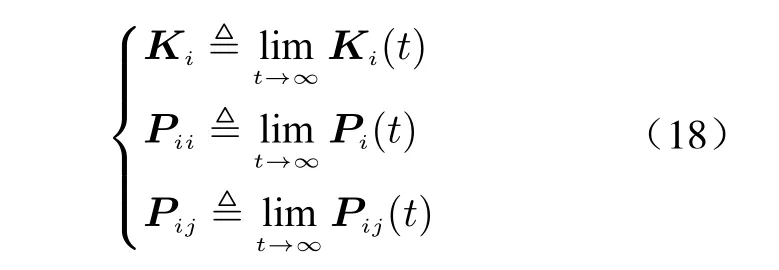
With such steady state design, the computation resource can be efficiently saved, since the procedures of real-time recursive computation are greatly reduced. Thus, more time is reserved for the implementation of encryption scheme.

Then, to obtain the best estimation performance with LSEs, the optimal weighting matrix should be calculated in the linear minimum variance sense. Based on above steady-state Kalman design, corresponding steady-state weighting matrix is computed by

In order to counter malicious eavesdropping,LSEs in this paper are processed by Paillier homomorphic encryption approach. The original LSEs are replaced by encrypted LSEs for transmission. Thus, the fusion operations in FC will become

At last, the legitimate user will decrypt encrypted data (20) by using secret keys. The privacy-preserving fusion protocol using homomorphic encryption is given in Protocol 1. Then,we give the following theorem to show the privacy of proposed confidentiality estimator.

Theorem 1 Protocol 1 preserves the computational privacy against eavesdroppers, while the legitimate user obtains the optimal DFEs.

ˆxi(0),i=1,2,··· ,L Protocol 1 For given Sensors:1: Use KeyGen(λ) to calculate and distribute keys.2: Calculate LSEs by steady-state Kalman filters (15)-(18);[[ˆxi(t)]] pk 3: Calculate encrypted LSEs with ;

FC:1: Calculate weighting fusion matrices by (19);[[ˆxf(t)]]2: Calculate encrypted DFE by (20);[[ˆxf(t)]] sk ˆxu(t)1: Decrypt using to get ;

Proof Let us define the variables with (˜·) as those obtained by the simulator and differ from that of the views but follow the same distribution. Then, we respectively analyze the views of eavesdropper and legitimate user. Since DFEs of different steps are independent, we only describe the view of each time step, and the time indextis omitted.

First, we analyze the computation of eavesdropper. Let us denoteVsΠas the view of all sensors from 1 toL. It can be described as [18]

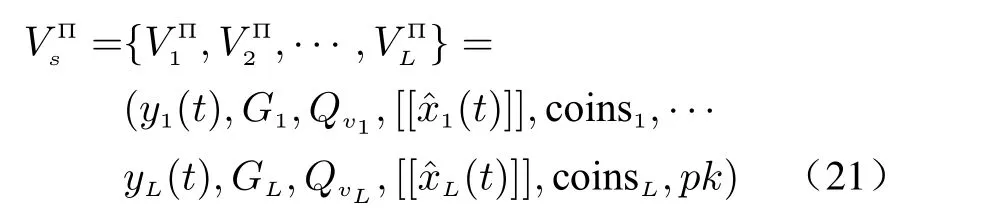
where coinsi(i=1,2,··· ,L) are random numbers used for the encryption process and key generation. Similarly, the view of FC is given

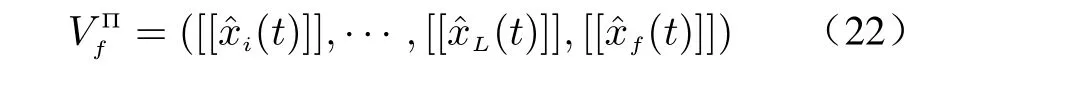
Since eavesdropper has access to the transmissions of sensors and FC, FC and legitimate user, its execution view can be described by

On the other hand, the legitimate user can decrypt message due to the private keysk. Based on the homomorphisms (11) and (13), the encrypted DFE (20) can be decrypted into

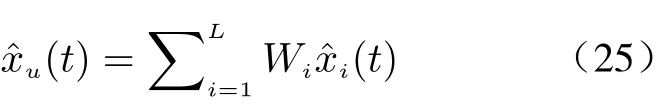
It can be found thatxˆu(t)≡xˆf(t). This means that the encrypted data [[xˆf(t)]] can be successfully decrypted toxˆf(t), which makes the optimal estimation performance of legitimate user. This completes the proof.

Remark 1 In the secure estimator design in[18], aggregator uses covariance intersection approach to fuse estimates of managers. To increase performance, the fusion criterion weighted by matrix is considered in this paper,which has higher accuracy due to the consideration of cross covariances. Meanwhile, the estimation systems are assumed to be steady-state at start, which reserves the time for encryption process, since the recursive calculation of estimator gain is reduced.

4 Simulation

In this section, we consider a target tracking system that is observed by two sensors as a simulation example, since unmanned vehicles imperatively require privacy protection in recent years.The state vector is constructed asx(t)=col{s(t),s˙(t)}, wheres(t) ands˙(t) respectively represent the position and velocity of a maneuvering target at timet. According to the dynamics and observations of vehicles, the system parameters in (1) and (2) are given by [7]

We compare the proposed method with distributed fusion estimator in [18], which uses

covariance intersection as fusion criterion. In Fig. 1 and Fig. 2, the trajectories of real states and estimates are plotted. We can intuitively see from this figure that the proposed DFE can track the maneuvering target well under homomorphic encryption, including position and velocity. Then,due to the existence of random noises, we assess the estimation performance by the root mean square errors (RMSEs) with Monte Carlo method over an average of 1 000 runs. Based on such metric, the performance of various estimators is shown in Fig. 3. It can be seen from this figure that the RMSE of DFE is lower than that of all the LSEs, which indicates DFE effectively fuses information from all sensors. Meanwhile,the RMSE of DFE in [18] is higher than that of proposed DFE. It demonstrates the better performance of the proposed fusion criterion.

Fig. 1 The positions of real state and DFE

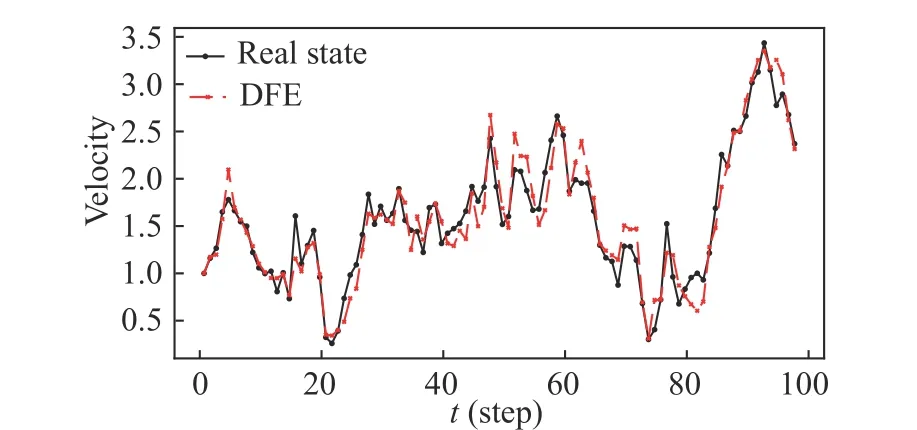
Fig. 2 The velocities of real state and DFE

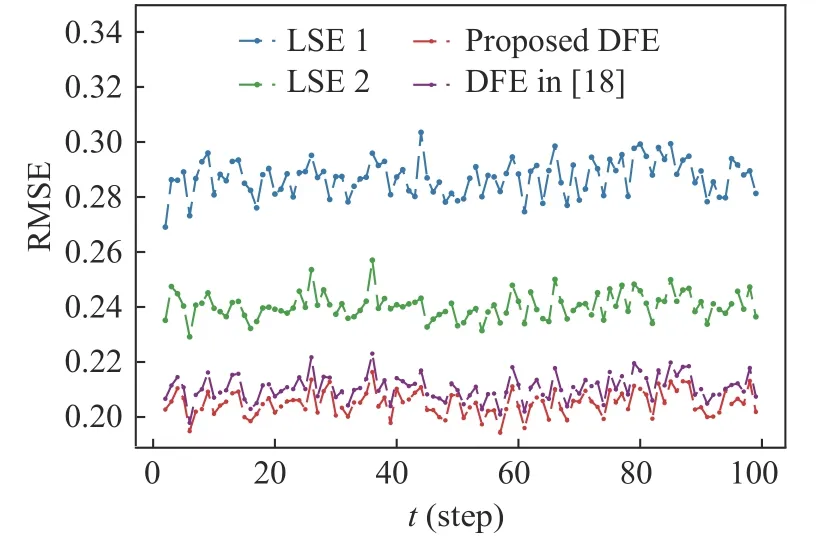
Fig. 3 The RMSEs of various estimators

5 Conclusion

In this paper, the distributed fusion estimation problem has been studied for a class of NMFS under eavesdropping attacks. By using Paillier homomorphic encryption approach, we designed a distributed privacy-preserving fusion estimator,where the transmitted LSEs were encrypted with public keys at each sensor node. Then, the encrypted local data were received and utilized for calculating encrypted DFEs in FC, which implies the invisibility of real DFEs to FC. By resorting to the private key, legitimate user successfully decrypted the encrypted DFE that was sent from FC, so it obtained the optimal estimation performance. On the other hand, the computational indistinguishability was guaranteed on the basis of cryptographic definitions. Finally, a maneuvering target tracking system was used to demonstrate the effectiveness of proposed method.