基于综合预测模型和蒙特卡洛的电动汽车保有量及负荷预测方法研究*

李 楠, 马宏忠

(河海大学 能源与电气学院,江苏 南京 211100)

0 引 言

随着化石能源的日渐短缺，以电动汽车为代表的新能源汽车成为未来汽车行业发展的方向[1-2]。由于政策支持和技术推动，电动汽车前景可观，近年来其保有量呈现高增长状态。2014年，我国电动汽车销量仅为7.4万辆，而2018年，电动汽车销量达到125.6万辆，出现15倍以上的爆发式增长。近年来因疫情等因素影响，电动汽车市场有所收缩，但仍保持一定增长，2021年全年电动汽车销量达到136.7万辆[3]。然而，电动汽车大规模接入电网势必加剧电力系统的不稳定性，因此，对电动汽车保有量以及充电负荷预测具有重要意义。

针对电动汽车保有量预测，现有方法大多采用单预测模型。文献[4]建立基于Bass模型和GM(1,1)模型的电动汽车保有量预测模型，对我国2020～2030年的电动汽车保有量进行预测。文献[5]利用Bass模型和灰色Lotka-Volterra模型对电动汽车短期保有量进行预测，并对政府政策扶持方法和电动汽车发展前景提出相关建议。文献[6]采用弹性系数法和千人保有量法建立电动汽车保有量预测模型，对陕西省电动汽车保有量进行预测。上述文献在参数估计的基础上利用单预测模型对电动汽车保有量进行预测，可以根据预测中偏大或偏小的趋势预测变化效果，但随着预测步长的加长，预测误差将逐渐增大。相较于单预测模型，综合预测模型能够结合各单预测模型的优点，并利用权重分配方法，进一步提高预测准确率。目前，综合预测已经广泛应用于其他各个领域。文献[7]建立基于k-SVD-OMP和KELM组合方法的短期光伏功率预测模型，得到了较好的预测结果和精度。文献[8]提出一种基于极端梯度提升和长短时记忆(LSTM)网络模型的短期光伏出力组合预测模型，对2018年光伏电站人工运维大数据进行预测。文献[9]建立非线性状态估计和神经网络组合的预测模型，对风电机组故障情况进行预测。

针对电动汽车负荷预测，现有研究主要集中于负荷时空分布特性。在统计大量交通信息的基础上，形成一条涵盖用户出行目的、出行时间和活动数量等相关信息的出行链，建立出行链理论，从而完成负荷预测。文献[10]提出一种基于图WaveNet的电动汽车充电负荷预测框架，利用耦合电网-交通网内相关信息对充电站充电负荷进行预测。文献[11]提出一种考虑季节特性的多时间尺度电动汽车负荷预测模型，对未来数年电动汽车的发展趋势以及考虑季节特性的多时间尺度电动汽车负荷进行预测。但是上述方法无法考虑空间分布上的随机性和波动性，且缺少准确的未来电动汽车保有量数据，实际应用效果不佳，预测准确率不高。而基于蒙特卡洛的电动汽车负荷预测方法，可以分析用户的出行习惯以及用户的使用习惯，形成起始充电时间和出行时刻等相关数据的概率分布。采用蒙特卡洛算法模拟用户出行，从而对某一地区负荷进行预测，可以有效反映电动汽车空间分布上的随机性以及波动性。

综上所述，本文建立基于综合预测模型和蒙特卡洛的电动汽车保有量以及负荷预测模型。组合灰色预测、反向传播(BP)神经网络和LSTM网络模型，并利用熵权法分配3种单预测模型预测结果，得到综合预测结果。基于2022年电动汽车保有量，采用蒙特卡洛算法，分析电动汽车起始充电时间等用户出行特征，对电动汽车规模化接入电网后的负荷变化进行预测。

1 电动汽车保有量预测模型

预测模型对预测结果具有重要影响，选用合适的预测模型可以有效提高预测精度。时间序列数据具有非周期、非线性以及非平稳等复杂性，为兼顾不同预测模型在预测过程中的优势，本文组合灰色预测、BP神经网络以及LSTM网络3种方法对电动汽车保有量进行预测。综合预测模型可以表示为

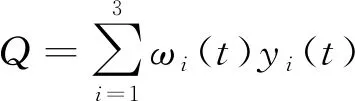
(1)

式中：yi(t)为灰色预测、BP神经网络以及LSTM网络的预测结果；ωi(t)为灰色预测、BP神经网络以及LSTM网络的权重，和为1。

1.1 单预测模型

电动汽车数据具有线性、周期性以及复杂性等不同特性，灰色预测模型对线性数据具有较强的适应性，BP神经网络模型在周期性时间序列数据上效果较好，LSTM网络模型能够较好地对复杂时间序列数据进行预测。

1.1.1 灰色预测

灰色预测是用来预测灰色系统的预测方法。其通过寻找已知数据的规律，生成有较强规律性的数据序列，建立相应的微分方程模型，从而对未来的发展趋势进行预测，可表示为

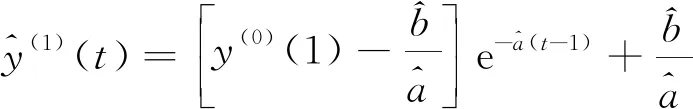
(2)

1.1.2 BP神经网络

BP神经网络根据所给的训练样本输入和输出向量不断学习，并对神经元之间的权值和阈值进行调整，使网络不断逼近样本输入和输出之间的映射关系，再通过测试样本来预测结果的准确性。首先定义输出误差信号：

ej(n)=dj(n)-yj(n)

(3)

式中：yj(n)为神经元j在n步迭代的实际输出值；dj(n)为期望输出值。

定义代价函数：

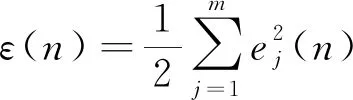
(4)

权值调整公式为

wji(n+1)=wji(n)+Δwji(n)

(5)

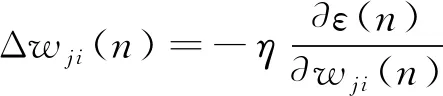
(6)

式中：η为学习率参数。

最后输出结果：

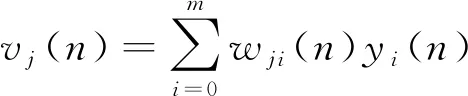
(7)

yi(n)=φ[vj(n)]

(8)

式中：φ(x)表示神经元非线性激活函数。

1.1.3 LSTM网络

LSTM网络在传统递归神经网络的基础上，增加了具有记忆单元的神经网络层，包括输入门、输出门和遗忘门3个模块，增加了对时间序列数据预测的记忆能力，广泛应用于时间序列数据的预测。

输入门负责保存记忆单元中的相关信息，其更新公式为

it=sigmoid(aixxt+aihht-1+aicCt-1+bi)

(9)

式中：sigmoid为激活函数；aix、aih、aic为输入门权重系数；xt为t时刻的输入；ht-1为t-1时刻的输出；Ct-1为t-1时刻的候选向量；bi为输入门偏置。

输出门负责输出记忆单元中的相关信息，只输出算法所需信息，其更新公式为

Ot=sigmoid(aoxxt+aohht-1+aocCt-1+bo)

(10)

式中：sigmoid为激活函数；aox、aoh、aoc为输入门权重系数；xt为t时刻的输入；ht-1为t-1时刻的输出；Ct-1为t-1时刻的候选向量；bo为输出门偏置。

遗忘门负责丢弃记忆单元中的相关信息，其更新公式为

ft=sigmoid(afxxt+afhht-1+afcCt-1+bf)

(11)

式中：sigmoid为激活函数；afx、afh、afc遗忘门权重系数；xt为t时刻的输入；ht-1为t-1时刻的输出；Ct-1为t-1时刻的候选向量；bf为遗忘门偏置。

1.2 组合权重

不同数据的权重分配组合具有不同类型，主要分为主观赋权和客观赋权。主观赋权往往容易受到人为因素的干扰，预测结果与实际结果存在较大偏差，因此本文采用客观赋权的方法，对单预测模型预测结果进行组合。熵权法在客观赋权方法中应用效果最佳，其利用不同模型预测的保有量数据计算信息熵大小，对不同预测模型所占权重进行分配，可以最大程度地保存有效信息。

对于m个对象，将每个传感器采集的n维数据进行拼接，构成矩阵X：

(12)

对X进行一次标准化，可以得到Z，其中标准化公式为

zij=

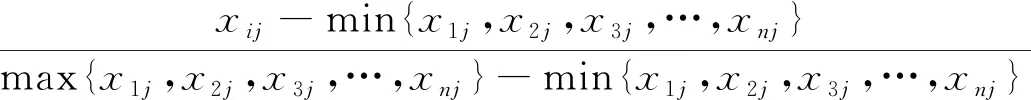
(13)

对j个指标而言，信息熵计算公式为

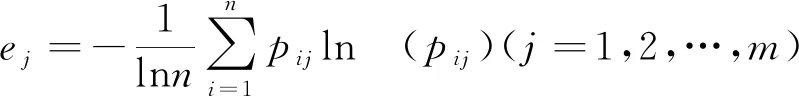
(14)

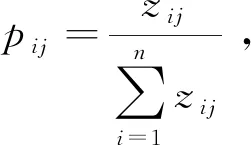
可得各模型熵权为

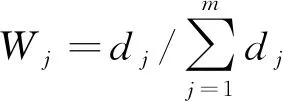
(15)

2 基于蒙特卡洛的电动汽车负荷预测模型

2.1 车辆出行时空模型分析

2.1.1 电动汽车起始充电时间

电动汽车的起始充电时间受到电动汽车的种类、用户个人出行习惯、汽车电池容量、季节以及节假日等多种因素的影响。基于国家统计局数据，本文对北京市交通数据进行调查，得到各类电动汽车起始充电时间的分布情况，如图1所示。起始充电时间可以分成0～12时和12～24时两个时间段。

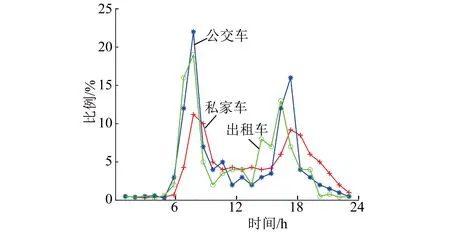
图1 电动汽车起始充电时间分布图

本文利用SPSS软件拟合电动汽车起始充电时间分布数据得，电动汽车起始充电时间在0～12时和12～24时两个时间段内符合以下概率密度函数，即符合正态分布，具体拟合参数如表1所示：

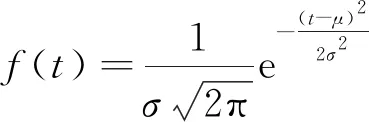
(16)

式中：σ为起始充电时间的方差；μ为起始充电时间的均值。

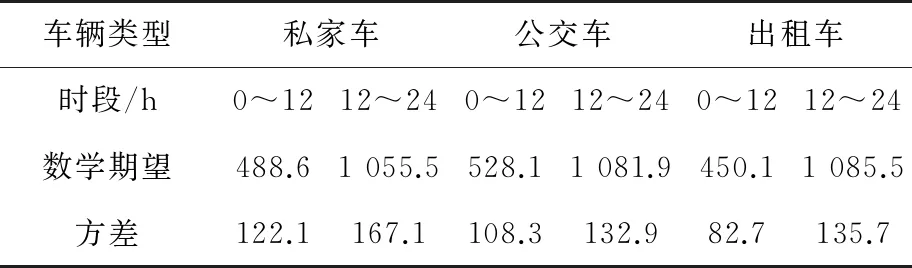
表1 起始充电时间拟合参数

2.1.2 车辆日行驶里程

私家车的出行里程受到多种因素的影响，其出行主要应用于工作及娱乐。如图2所示，本文统计某市私家车日行驶里程，可得工作日与休息日的行驶里程存在明显差别。

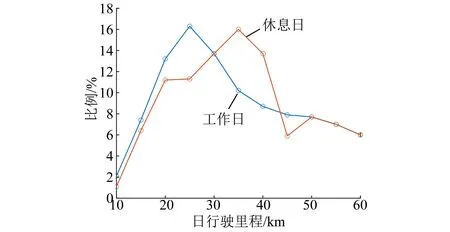
图2 电动汽车日行驶里程分布图

本文利用SPSS软件拟合电动汽车日行驶里程，其分布符合以下概率密度函数，即伽马分布：

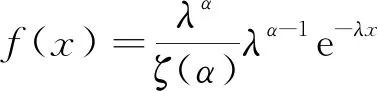
(17)

式中：ξ(α)为伽马函数；λ和α分别为尺度和形状参数，其中工作日λ=0.045、α=1.6，节假日λ=0.031、α=1.8。

出租车的日行驶里程较为复杂。受到出租车司机的班次选择和城市需求等因素的影响，平均日行驶里程在300～600 km之间。本文统计某市出租车日行驶里程，可知出租车日行驶里程可以分成0～15时和15～24时两个时间段，利用软件对出租车的日行驶里程进行拟合，可知其符合正态分布，其拟合参数如表2所示。

表2 日行驶里程拟合参数

公交车的日行驶里程比较均匀，主要取决于公交车的固定线路长度、发车密度、路阻程度和运营时间等因素。分析调查数据可知，公交车平均行驶里程均在140～200 km范围内，并且呈现随机分布的特性，因此本文假设公交车的日行驶里程服从均匀分布[140,200]。

2.2 车辆出行时空模型分析

本文假设整个行驶过程的用电率相同，基于蒙特卡洛模拟电动汽车的充电负荷模型，对于电动汽车用户的习惯进行仿真，随机抽取包括电动汽车起始充电时间、电动汽车充电功率和电动汽车日行驶里程等参数，算法流程图如图3所示。

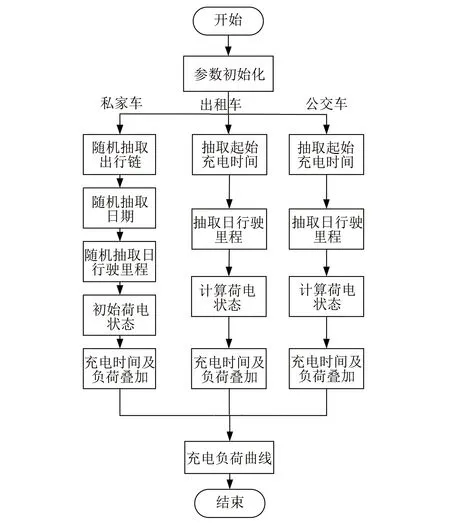
图3 电动汽车负荷预测流程图

根据上述数据分析的相关参数，确定仿真的次数、仿真电动汽车的保有量和电动汽车类型所对应的最大行驶里程，完成模拟仿真的程序参数初始化。初始电动汽车荷电状态(SOC)计算式为

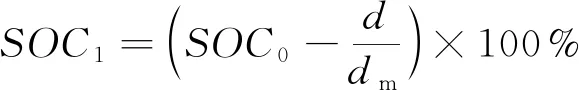
(18)

式中：SOC1为本次充电开始时的电池荷电状态；SOC0为上次充电完成时的电池荷电状态；d为本次行驶的里程；dm表示车辆最大行驶里程。

充电所需时间为

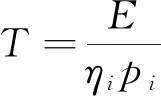
(19)

式中：E为第i类电动汽车的电池容量；ηi为第i类电动车的充电效率；pi为第i类电动车的充电功率。

各个负荷节点的充电功率为

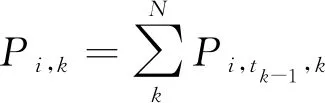
(20)

式中：Pi,k为第i类电动汽车在第k个节点的充电功率之和；Pi,tk-1,k为第i类电动汽车中满足充电起始时间大于tk-1的车辆的充电功率。

节点负荷功率叠加为

Pk=Pcar,k+Pbus,k+Ptaxi,k

(21)

式中：Pcar,k、Pbus,k、Ptaxi,k分别为私家车、公交车和出租车在第k个节点的充电功率之和；Pk表示第k个节点的充电功率之和。

3 算法验证

3.1 电动汽车保有量预测

本文以某市电动汽车实际数据为基础，利用构建的综合预测模型预测该市的电动汽车保有量情况，并以此为基础利用蒙特卡洛算法模拟电动汽车充电日负荷情况。

表3为2012～2021年某市电动汽车保有量数据，以此为基础,利用本文方法进行拟合，并与真实数据对比，验证本文所提模型的有效性。如图4所示，本文所提模型对不同类型车辆均具有较高的准确度。

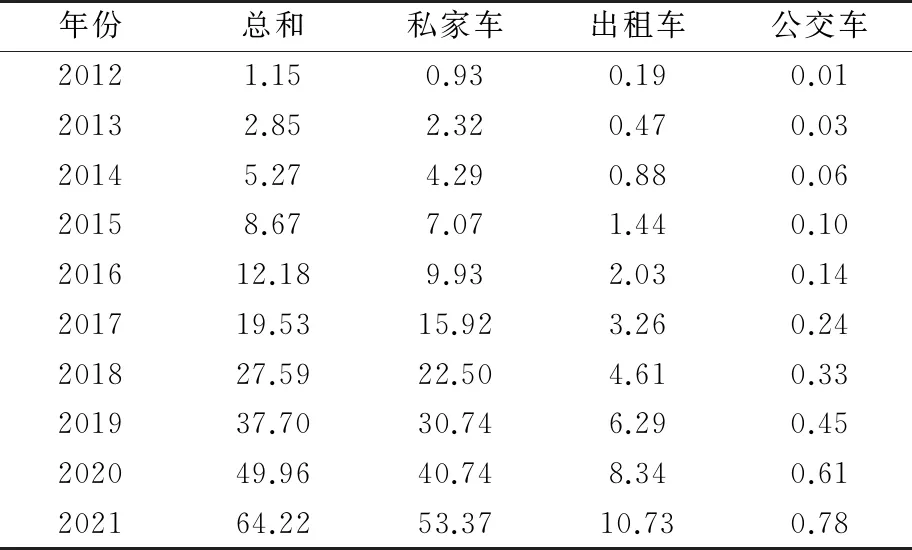
表3 2012～2021年某市电动汽车保有量 万辆

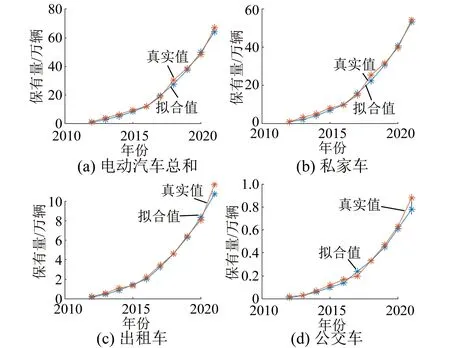
图4 电动汽车保有量拟合图

为进一步验证本文所提综合预测模型的优越性，与灰色预测、BP神经网络以及LSTM网络3种模型对比，如图5所示。由图5可知，本文所提模型更贴近真实值，综合预测模型、灰色预测模型、BP神经网络模型以及LSTM网络模型的拟合优度分别为0.98、0.90、0.92和0.56，可知本文所提模型具有更高的准确度。

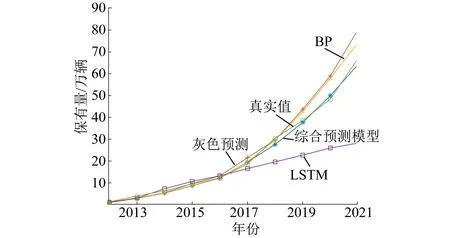
图5 各预测模型对比图

基于上述的综合预测模型，对2022～2024年某市电动汽车保有量进行预测，预测结果如表4所示。

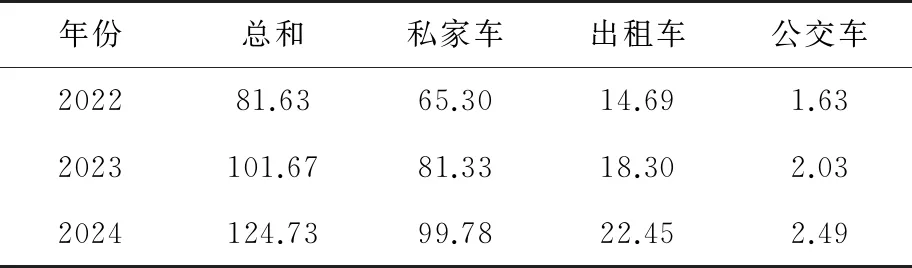
表4 2022～2024年某市电动汽车保有量 万辆

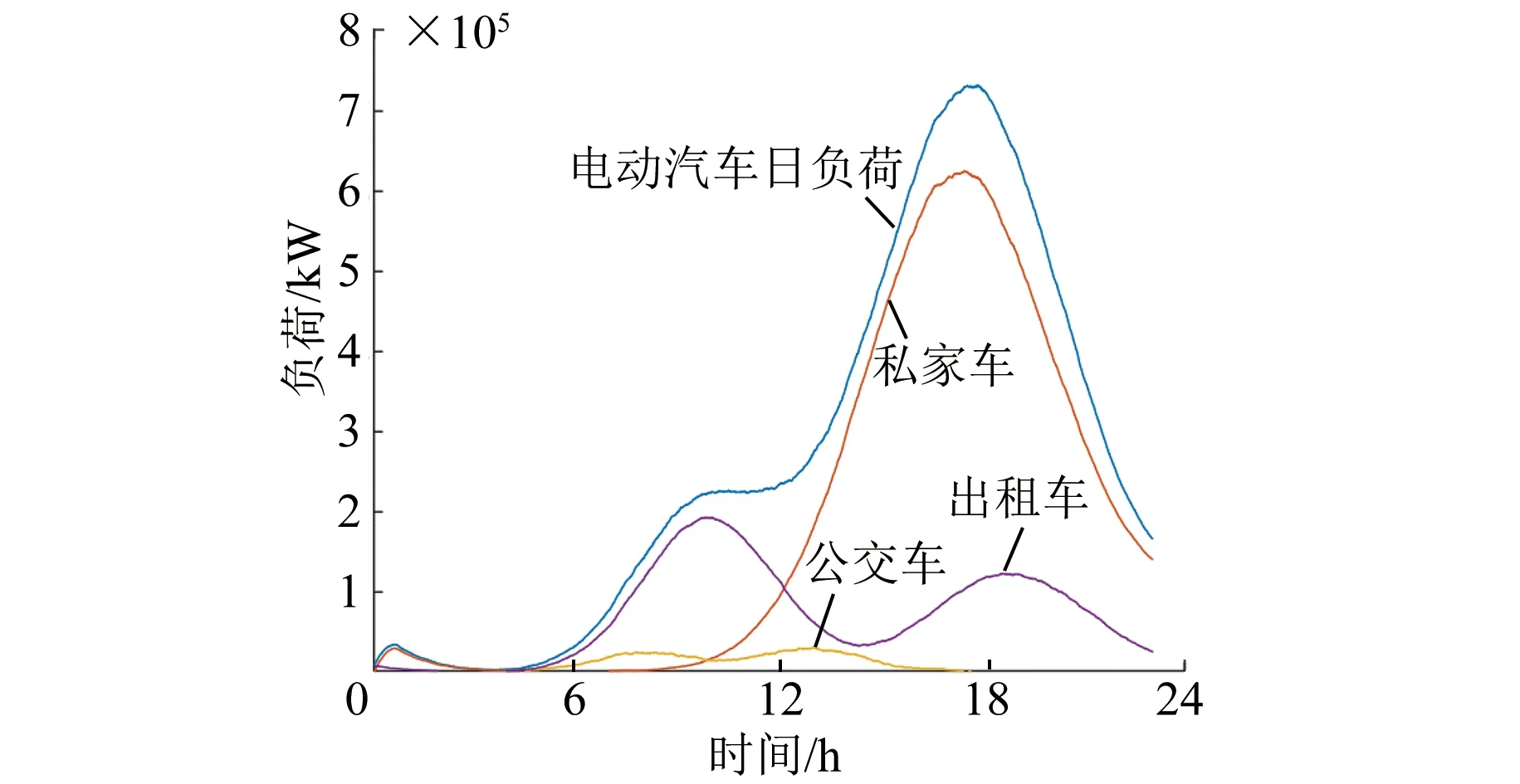
图6 电动汽车负荷预测图

3.2 电动汽车日负荷预测

基于2022年电动汽车保有量，根据起始充电时间、日行驶里程以及充电功率等出行特性，预测电动汽车工作日的日负荷。如图6所示，私家车的充电负荷高峰期主要集中在城市居民下班回家之后的19～22时之间。出租车和公交车的充电时间相对来说比较分散，但也存在小的高峰。总负荷在19～22时期间较大，可知私家车负荷占很大部分。此情况下可以通过价格引导等方式，鼓励用户错峰充电，以缓解用电压力，提高电网利用率。

将电动汽车日负荷曲线与该市电网的负荷曲线叠加，如图7所示。电动汽车大规模接入电网后，势必加剧电网的峰谷差，电网的负荷曲线峰谷差越大，对电力系统的安全稳定运行带来的风险越多。因此考虑采用V2G技术，负荷低谷时电动汽车充电，负荷高峰时电动汽车放电，以削弱电网峰谷差。

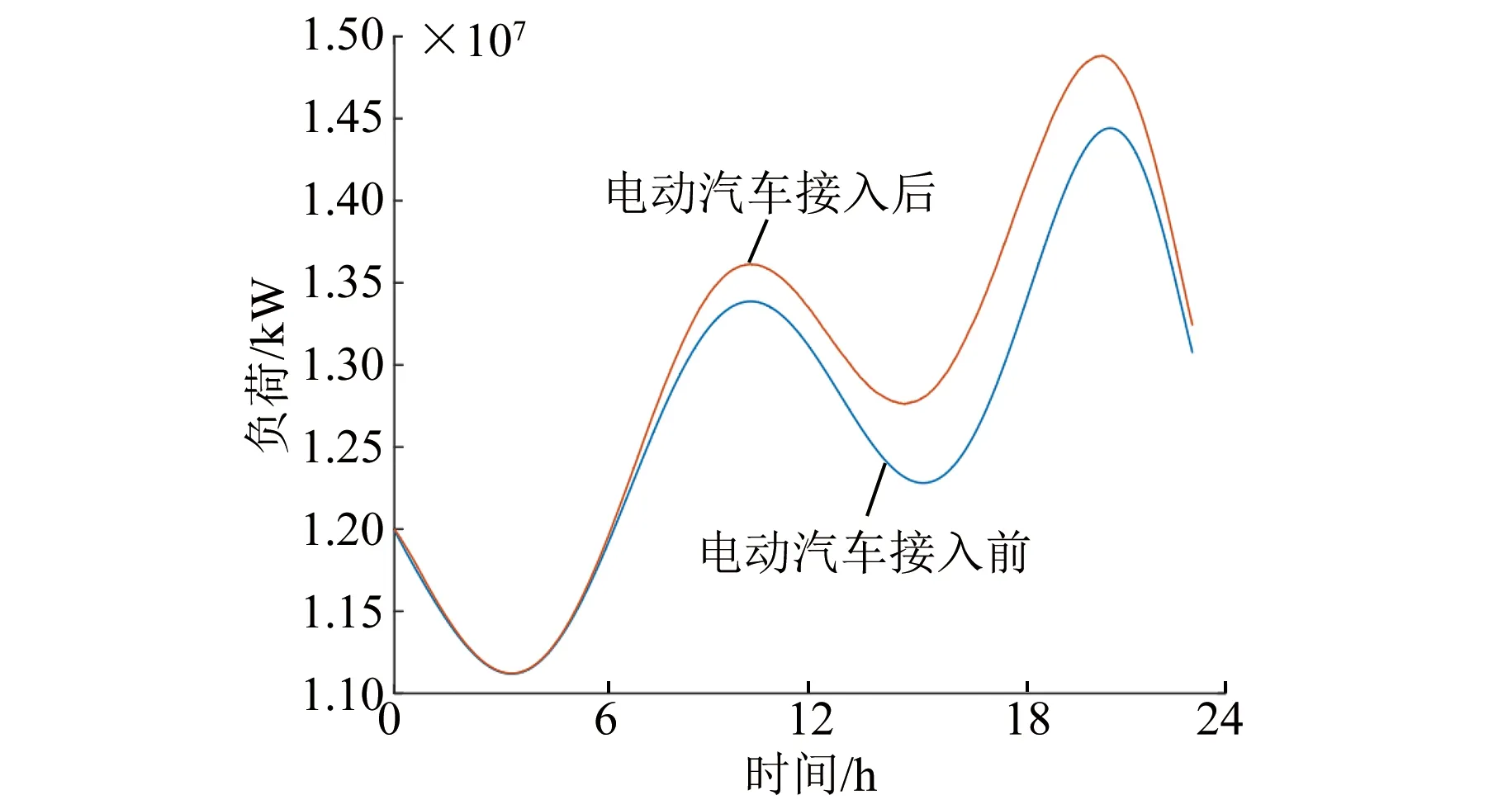
图7 电动汽车大规模接入电网前后对比图

4 结 语

电动汽车大规模接入电网给电力系统的安全稳定运行带来新的隐患。本文建立基于综合预测模型和蒙特卡洛的电动汽车保有量和负荷预测模型，对某市电动汽车保有量和负荷情况进行预测，得到如下结论。

(1) 针对单预测模型预测精度不高的问题，建立电动汽车保有量综合预测模型，结合灰色预测模型、BP神经网络模型以及LSTM神经网络模型的优势，并利用熵权法组合各预测模型权重，取得了良好的预测结果，预测准确率高达98%，比单预测模型至少提高了6%。

(2) 针对现有电动汽车负荷预测方法多集中于时间分布，未考虑空间位置的随机性和波动性的问题，提出基于蒙特卡洛的电动汽车负荷预测方法，分析结果表明电动汽车大规模接入势必加大电网的峰谷差，严重加剧电力系统的不稳定性。

此外，将在后续研究中统计真实的电动汽车实时负荷数据，与本文所提方法的预测结果进行对比，进一步验证本文所提方法的有效性。