标准地铁牵引PMSM初始位置辨识算法研究与应用

岳学磊, 高 闯, 田 地, 许克磊, 李康乐, 王晓飞

(西安中车永电捷通电气有限公司，陕西 西安 710016)

0 引 言

适用于系列化中国标准地铁列车的永磁牵引系统因其具有高效率、高功率密度等特点，成为新一代轨道交通牵引系统的发展方向[1]。其中永磁同步电机(PMSM)转子初始位置辨识的准确性，关系到起动转矩的大小及方向，当转子初始位置辨识误差较大时，磁场定向会发生较大偏差，导致电机起动失败甚至电机反转。当前PMSM转子初始位置辨识的方法主要有两种，一种利用PMSM自身的凸极特性，另一种基于PMSM定子铁心非线性饱和特性[2-4]。

文献[5]介绍了一种在电机静止时对转子位置进行辨识的方法，利用PMSM定子铁心的非线性磁化特性，通过给电机施加幅值相同、方向不同的一系列电压脉冲，检测并比较其响应的定子电流来辨识转子位置。试验表明此方法确实能有效地辨识出转子初始位置，但此方法依赖电压脉冲的幅值和作用时间，而且电机在辨识过程中可能会转动，对初始位置辨识精度产生影响。文献[6]提出一种优化选择电压矢量的脉冲电压注入法，对PMSM转子初始位置进行检测。其原理是根据多次脉冲电压作用的响应电流计算出含有位置信息的电感参数矩阵，从而计算出转子位置。该方法只需要施加5次电压脉冲即可确定转子初始位置，施加脉冲的次数较少，受电流采样误差的影响较小，其估算精度也不受转子初始位置影响。文献[7]提出在估算的同步旋转坐标系中注入高频正弦电压信号，通过闭环调节得出初次转子位置估算值；再利用不同磁极下d轴等效电路时间常数不同的特性，判断出d轴正方向，结合初次估算值得出正确的转子初始位置。该算法计算简单，易于实现，但需要参数整定。

为了得到准确的转子初始位置，本文首先采用高频方波电压注入算法获得转子的初次估计位置，然后分别在估计的d轴中注入正、反向电压窄脉冲，通过比较d轴正、反向响应电流幅值大小来判断此时定位的磁极为N极还是S极，如果定位的磁极是S极，则需要对初次估计位置进行补偿，使其定位在N极。通过仿真验证了该方法的准确性，并在多个位置对标准地铁PMSM进行转子初始位置辨识测试，将辨识结果与旋变实测值进行比较，证明了该辨识方法的可行性和实用性。

1 转子位置辨识算法

1.1 高频方波电压注入原理

为简化分析，作如下假设：

(1) 相绕组、定子电流和转子磁场均对称；

(2) 忽略磁场饱和，不计涡流损耗和磁滞损耗，气隙磁密波形为正弦波；

(3) 转子上无阻尼绕组。

在此基础上，PMSM在d-q同步旋转坐标系下的数学模型可以表示为

(1)

式中：ud、uq分别为同步旋转坐标系下的d、q轴电压；id、iq分别为同步旋转坐标系下的d、q轴电流；Ld、Lq分别为同步旋转坐标系下的d、q轴电感；Rs为定子电阻；ωe为电角速度；ψf为转子磁链；p为微分算子。

当电机静止或转速较低，且注入的方波电压信号频率远高于基波运行频率时，反电动势在定子电压中的占比很小，且不含高频成分，因此PMSM可近似等效为感性负载，式(1)可以简写为式(2)：

(2)

式中：udh、uqh分别为同步旋转坐标系下的d、q轴高频电压分量；idh、iqh分别为同步旋转坐标系下的d、q轴高频电流分量。

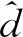
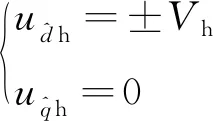
(3)

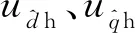
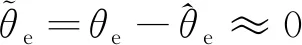
(4)

结合式(3)和式(4)将式(2)变换到静止坐标系中，得到静止坐标系中高频电流表达式为

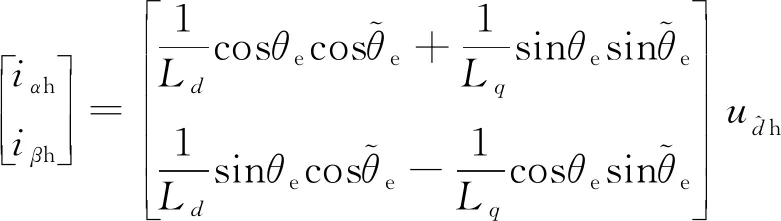
(5)

当转子位置估计误差近似为0时，式(5)可以简化为

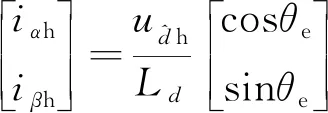
(6)

此时求得高频电流包络线(本次电流与上次电流的差值)为

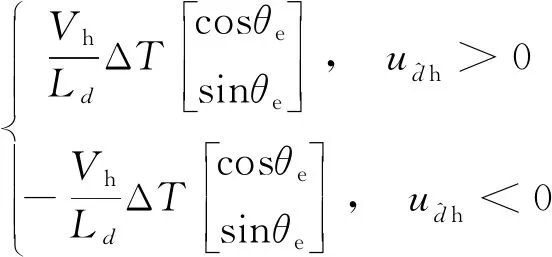
(7)

考虑到注入的高频方波电压信号的极性(正负)，式(7)可以表示为

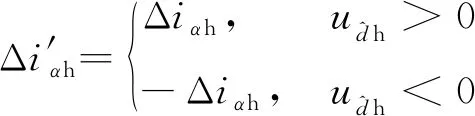
(8)

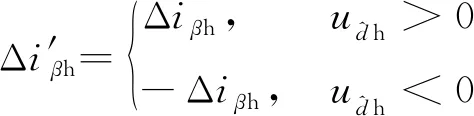
(9)

最终，静止坐标系中的高频电流包络线可以表示为

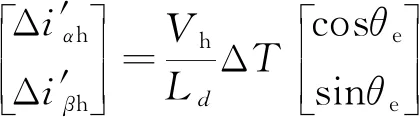
(10)

由式(10)可知α轴高频电流分量包络线表达式中包含实际转子位置的余弦值，β轴高频电流分量包络线表达式中包含实际转子位置的正弦值。高频响应电流包络线如图1所示。

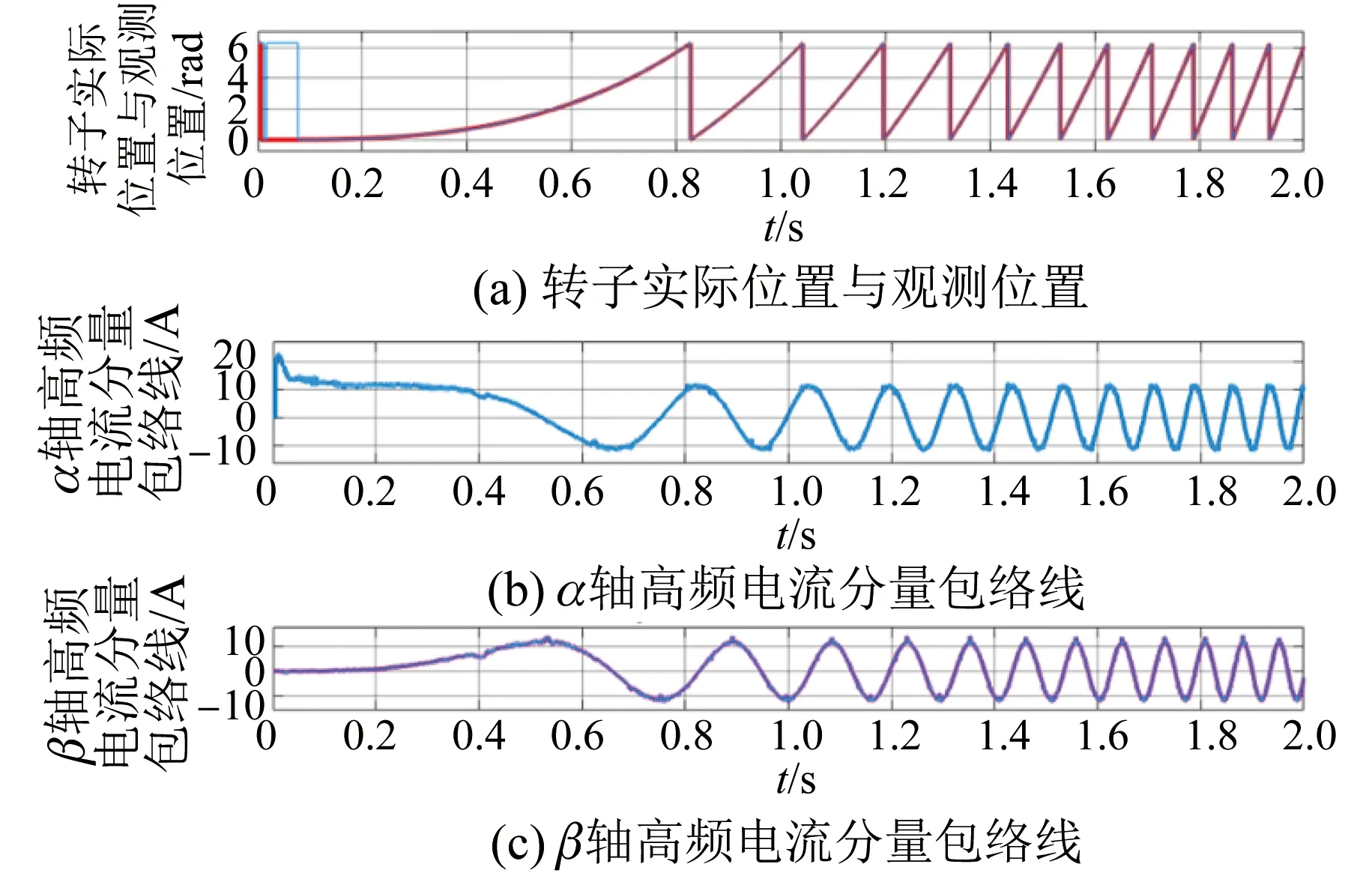
图1 高频响应电流包络线波形

由式(10)可知，通过提取高频电流分量包络线可以得到实际转子位置的余弦函数和正弦函数。当转子位置估计误差近似为0时，估计误差可以近似等于估计误差的正弦值，因此转子位置估计误差可由下式表示：

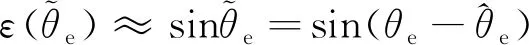
(11)

1.2 电流载波信号分离

为了避免带通滤波器(BPF)和低通滤波器(LPF)的使用，提高高频方波电压信号的注入频率，通过简单的代数运算分离出高频电流分量和基波电流分量。

本文采用的控制模式为双采样双更新模式，即在一个开关周期内采样两次电流，通过此方法可以将注入的高频电压频率提高到与开关频率一致。双采样双更新模式下注入电压信号和响应电流信号时序图如图2所示。

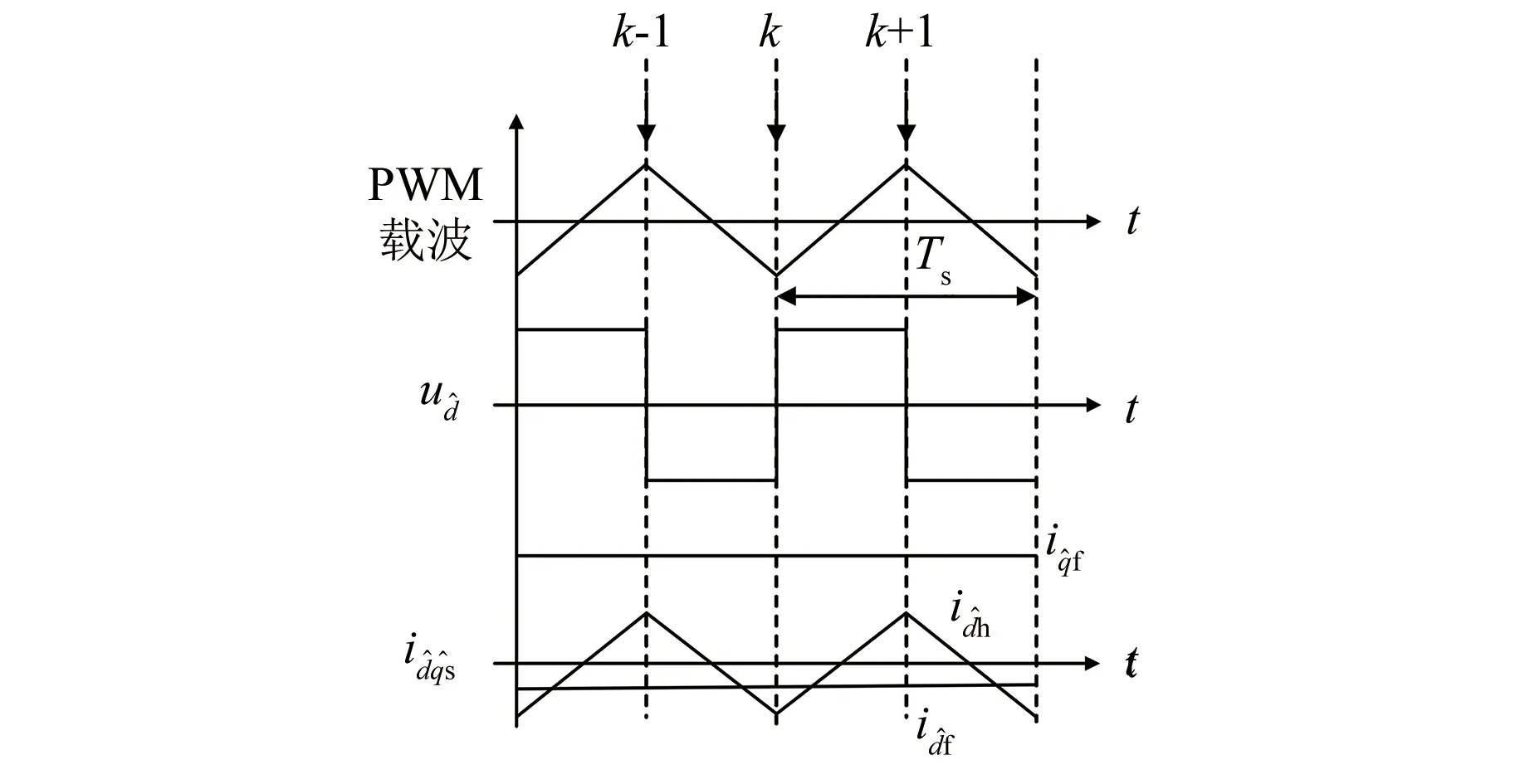
图2 双采样双更新模式下注入电压信号和响应电流信号时序图

在采样的电流信号中，忽略高频谐波电流，定子电流由高频响应电流与基波电流组成。由于注入的高频信号频率远高于基波运行频率(辨识初始位置的过程中电机基本不动)，因此在相邻采样时刻可认为基波电流信号不变，本周期电流与上周期电流之差的一半即为高频响应电流，具体可以表示为

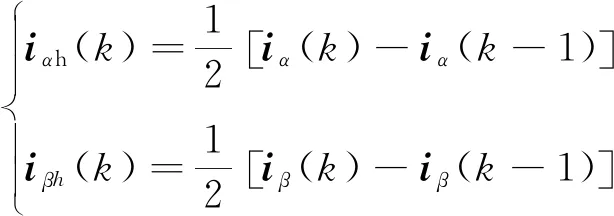
(12)

式中：iα(k)、iβ(k)分别为k采样时刻的α轴、β轴电流矢量；iα(k-1)、iβ(k-1)分别为k-1采样时刻的α轴、β轴电流矢量；iαh(k)、iβh(k)为k采样时刻的α轴、β轴高频响应电流矢量。

1.3 位置鲁棒观测器

在获得转子位置估计误差后，根据PMSM的机械运动方程构建位置观测器，将电磁转矩作为系统前馈项，从而提高观测器的动态响应性能。电磁转矩可以通过下式直接计算得到：

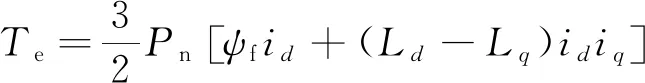
(13)

式中：Te为电磁转矩；Pn为电机极对数。

PMSM的机械运动状态方程为

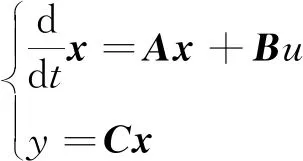
(14)

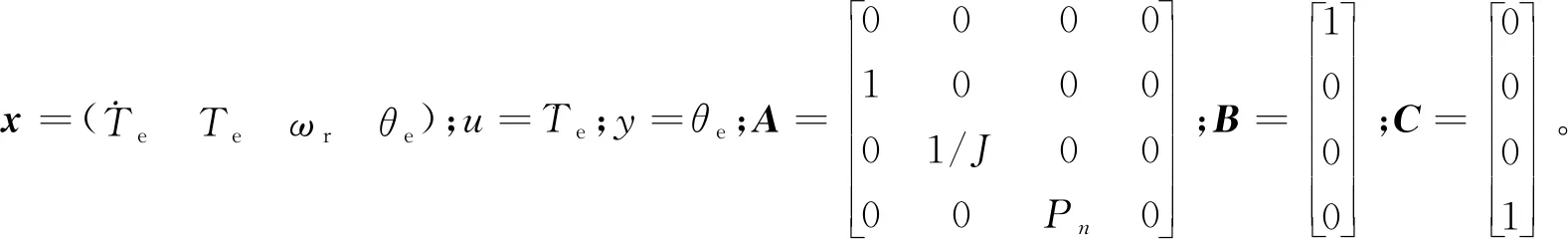
信息技术与课程整合的研究现状 笔者查阅相关文献发现，我国关于信息技术与课程整合的方法与实施策略的研究仍比较薄弱，很多中小学教师以及教育工作者不清楚信息技术与课程整合的模式、方法、实施策略等，在实际教学中不知道如何进行整合实践；而且目前的研究多数是将传统的教学模式和信息技术与课程整合的模式进行比较分析，鲜有研究把信息技术与课程整合的几种模式进行内部比较，这也是资源、设施的应用率比较低的原因之一。

则位置鲁棒观测器状态方程为

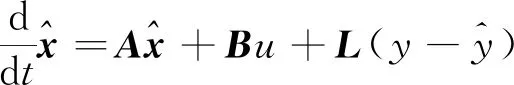
(15)

上式中L为反馈矩阵，其表达式为

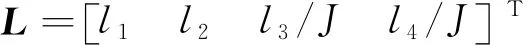
(16)

式中：l1、l2、l3、l4为系数，系数选取方法具体可参考文献[8]；J为转动惯量。

根据位置鲁棒观测器建立转子估计误差与扰动负载的传递函数[8]，公式如下：

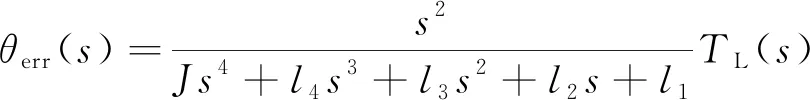
(17)

根据式(17)可以得到如图3所示的位置鲁棒观测器结构框图，观测器的输入为转子位置误差，输出为角速度和转子位置的辨识值。

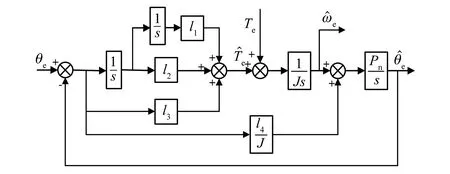
图3 转子位置鲁棒观测器结构框图

综上，构建转子位置初次辨识的控制结构框图，如图4所示。

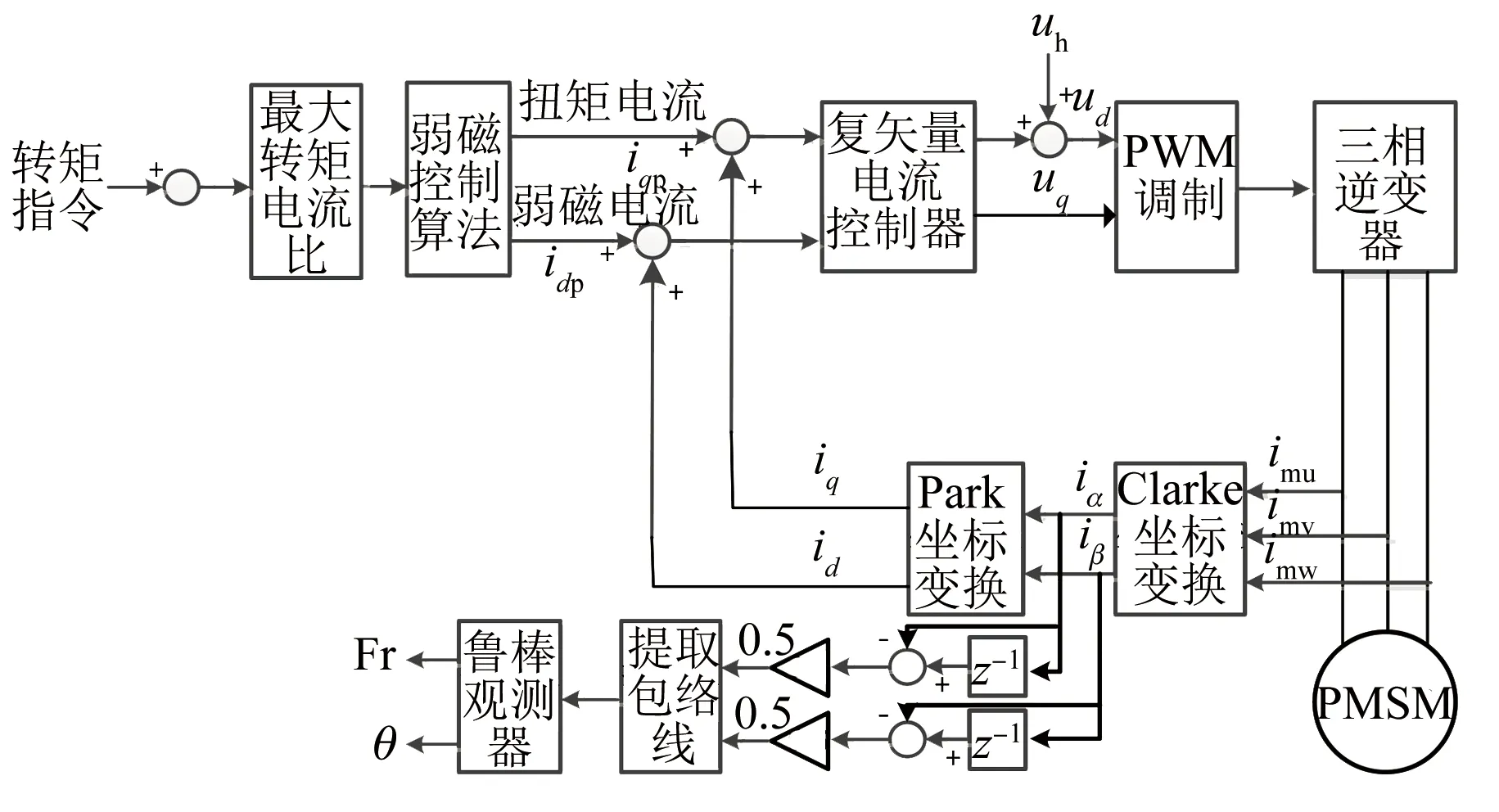
图4 PMSM转子位置初次辨识的控制结构框图

2 转子磁极极性判断算法

2.1 磁路饱和原理

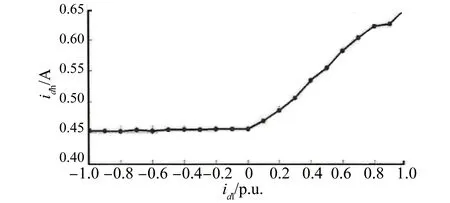
图5 d轴给定电流和响应电流关系图

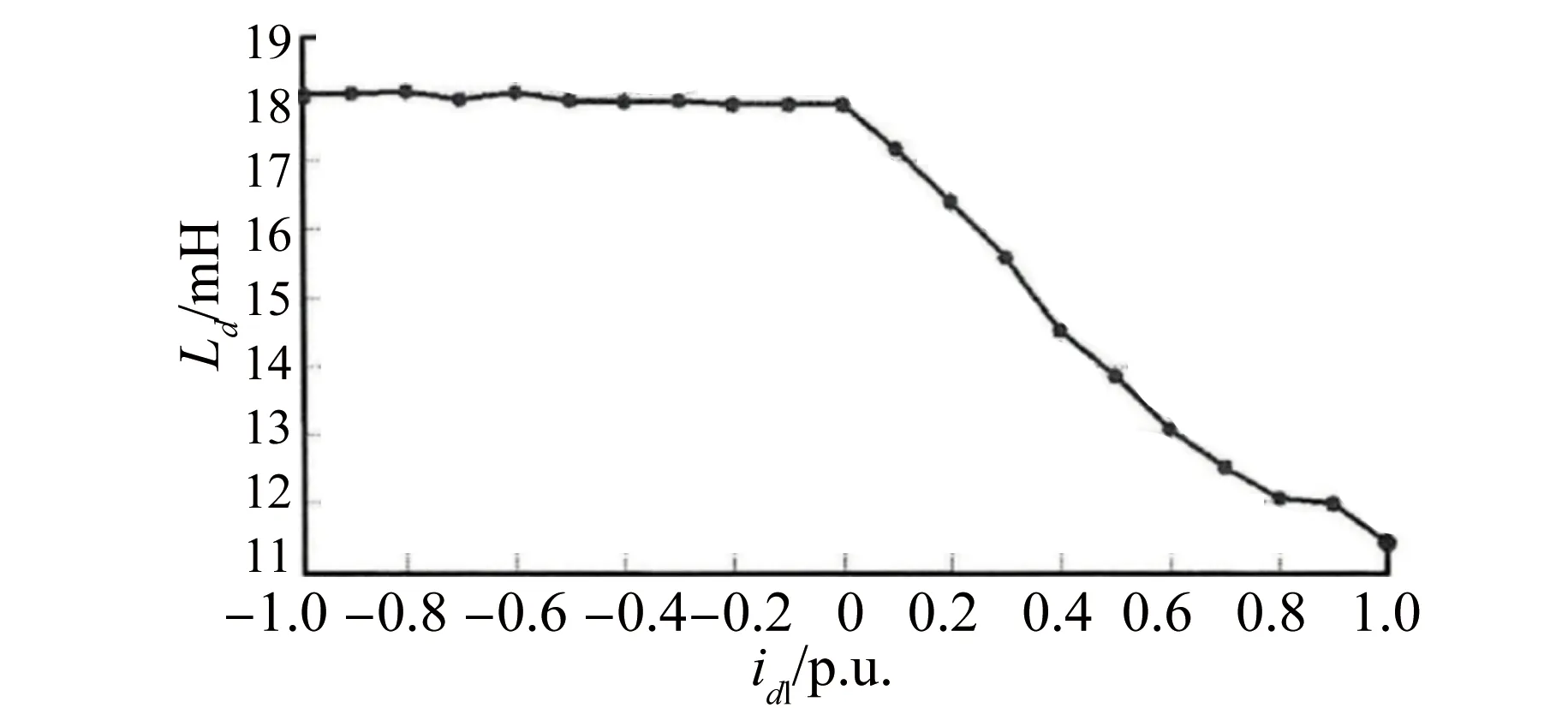
图6 d轴电流和电感关系图

从图5可以看出，当在d轴给定负的电流时，d轴响应电流几乎无变化，而在d轴给定正的电流时，d轴响应电流呈上升趋势。图6中，当在d轴给定负的电流时，电感几乎不变，而在d轴给定正的电流时，电感和d轴给定电流成反比。

综上可以得出，d轴响应电流的幅值随着定子铁心的饱和而改变，而此时的饱和程度又反而影响电感值。由于电感的变化，d轴电流响应的前后差值包含转子位置信息，但是对d轴给定电流本身来说，其差值很小，因此信噪比不高。

2.2 转子磁极极性判断算法

(1) 在估计d轴上注入两个周期的正电压脉冲，得到响应电流idF1；然后注入两个周期的负电压脉冲，得到响应电流idF2。idF1与idF2差值的绝对值即为正向的响应电流id1。延迟100个周期后，在估计d轴上注入两个周期的负电压脉冲，得到响应电流idF3；然后注入两个周期的正电压脉冲，得到响应电流idF4，idF3与idF4差值的绝对值即为负向的响应电流id2。

(2) 如果id1大于id2，则高频方波电压注入法所得初判的磁极位置极性为转子N极，不需要进行角度补偿，极性状态标志位设置2；如果id1小于id2，则高频方波电压注入法所得到初判的磁极位置极性为S极，需要进行π角度补偿，极性状态标志位设置1。转子磁极极性判断流程如图7所示。

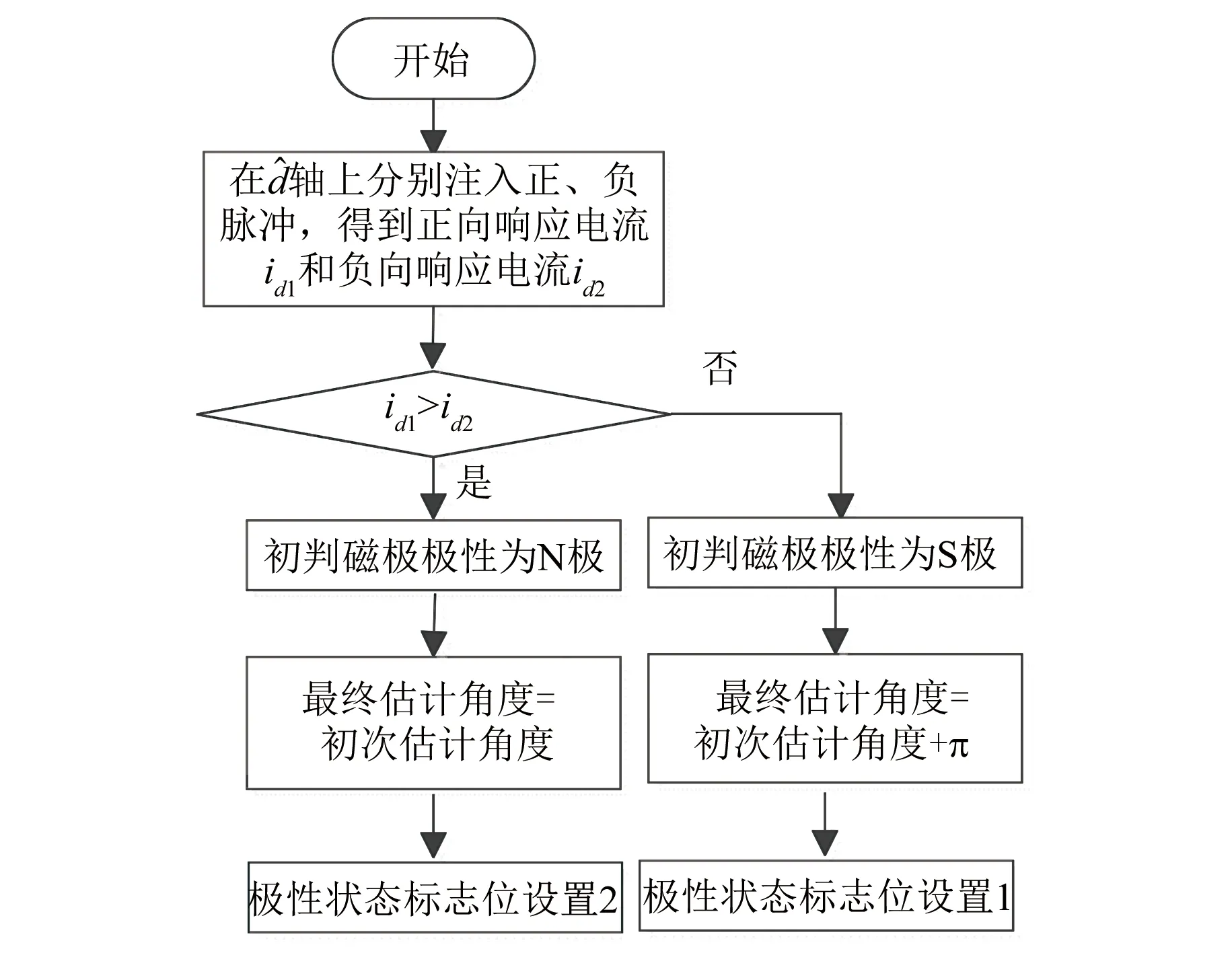
图7 转子磁极极性判断流程图

结合转子磁极极性判断算法与高频方波电压注入算法，就可以得到最终的转子位置辨识值，转子位置辨识的控制结构框图如图8所示。

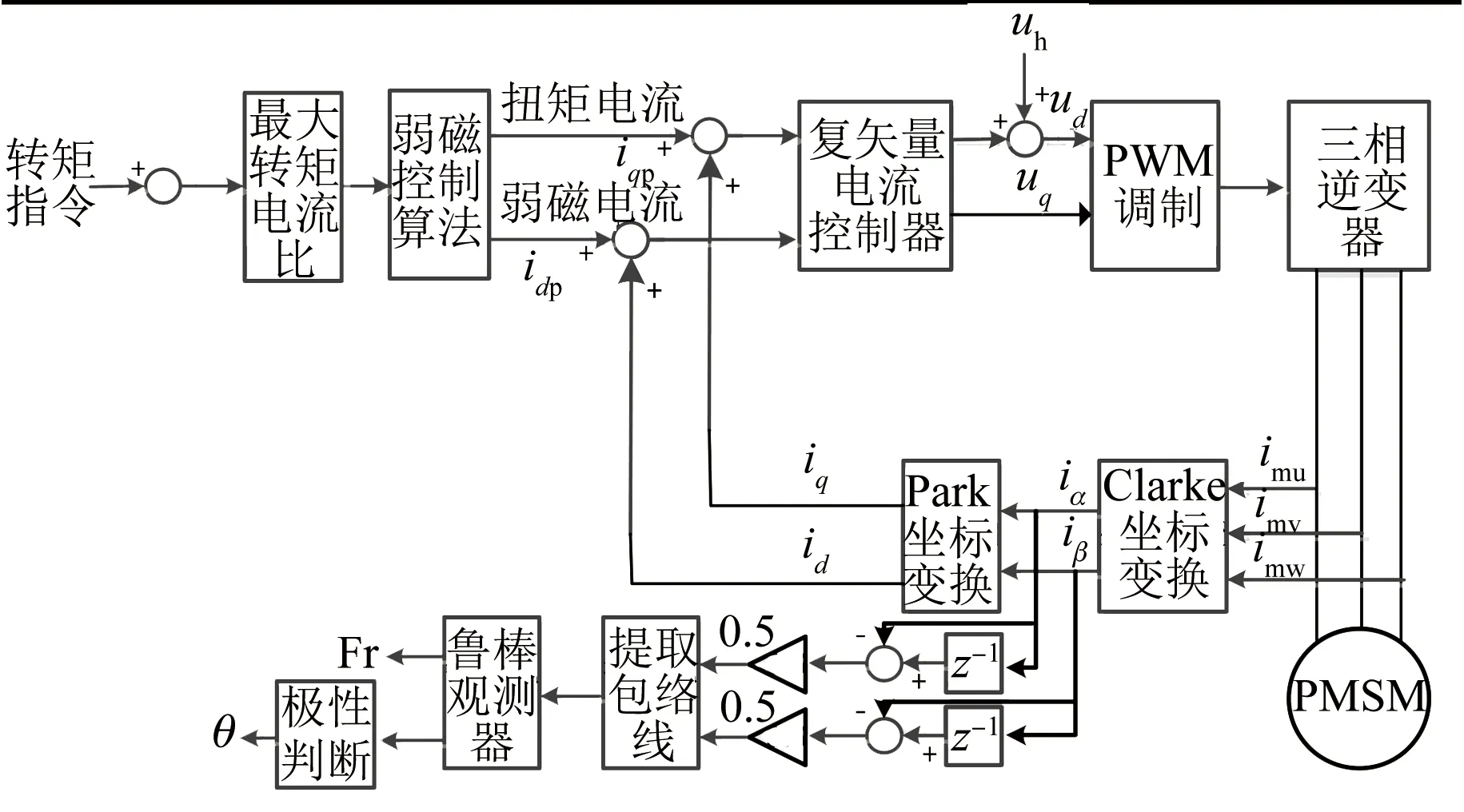
图8 PMSM转子位置辨识的控制结构框图

3 Simulink仿真与试验结果

3.1 Simulink仿真结果

为验证仿真状态下，转子初始位置辨识是否可靠，在Simulink仿真环境下，根据标准地铁主电路参数和PMSM参数，搭建基于永磁牵引控制系统的仿真模型，进行仿真测试。标准地铁主电路参数和PMSM参数如表1和表2所示。

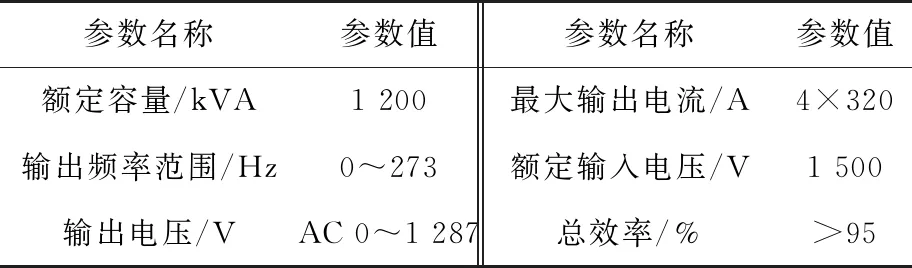
表1 标准地铁牵引逆变系统主电路参数

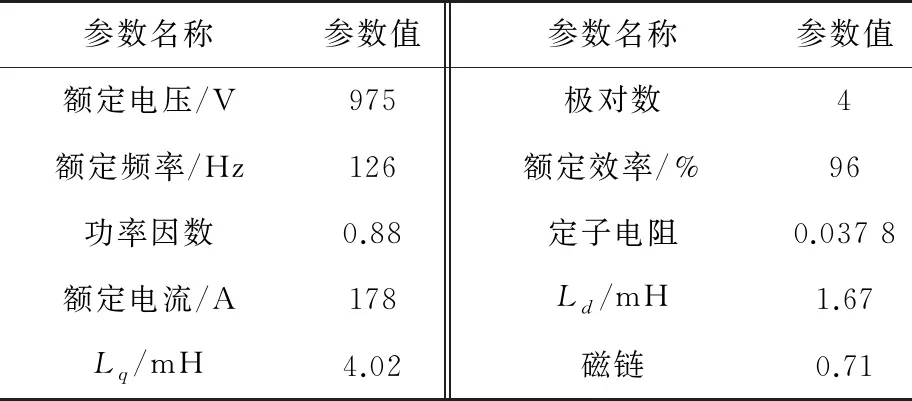
表2 标准地铁用PMSM参数

转子固定在1.4 rad位置，采用本文所提的转子初始位置辨识方法进行辨识。图9为转子磁极极性判断过程中的电流和电压波形，其中图9(a)为注入电压窄脉冲后得到的响应电流，图9(b)为注入的电压窄脉冲。

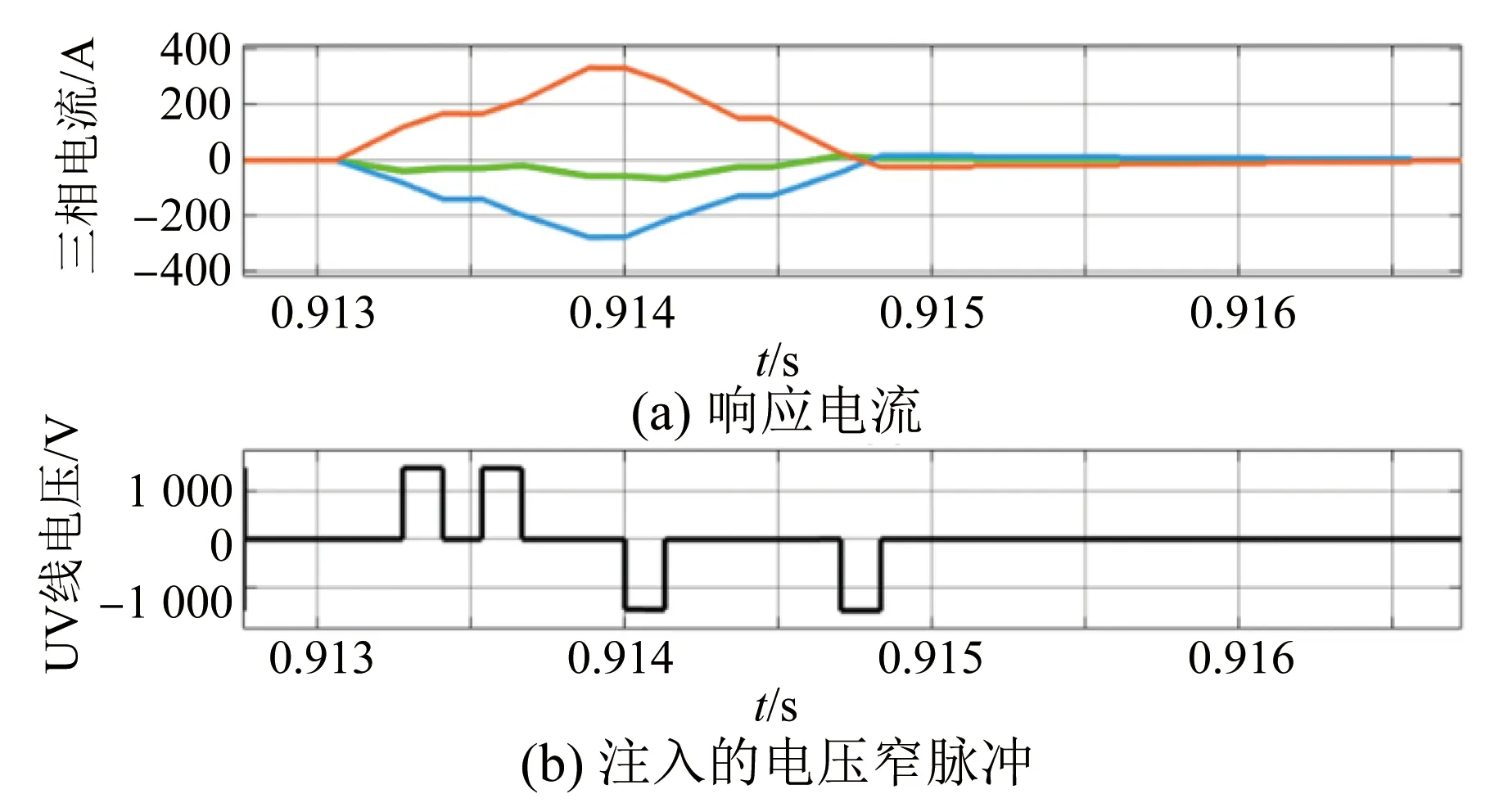
图9 转子磁极极性判断过程中的电流和电压波形

图10为转子初始位置辨识过程波形。从图10中可以看出，转子位置最终收敛值为1.414 9 rad，位置误差为0.014 9 rad，因为极性状态标志位为2，所以不需要加π处理。

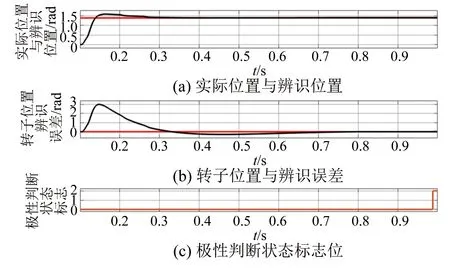
图10 转子初始位置辨识过程波形

3.2 组合试验结果

为验证初始位置辨识方法在标准地铁永磁牵引逆变系统中的性能，在中车大连电力牵引研发中心有限公司试验中心进行试验验证，图11为试验所用的标准地铁永磁牵引变流器及其他试验设备。

图11 试验所用的永磁牵引变流器

转子固定在5.183 6 rad，采用本文所提的转子初始位置辨识方法进行辨识。图12为转子磁极极性判断过程中的电压和电流波形，从上到下依次为UV线电压、UW线电压、U相电流和V相电流，图中的电压波形为注入电压窄脉冲，电流波形为注入电压窄脉冲后得到的响应电流。

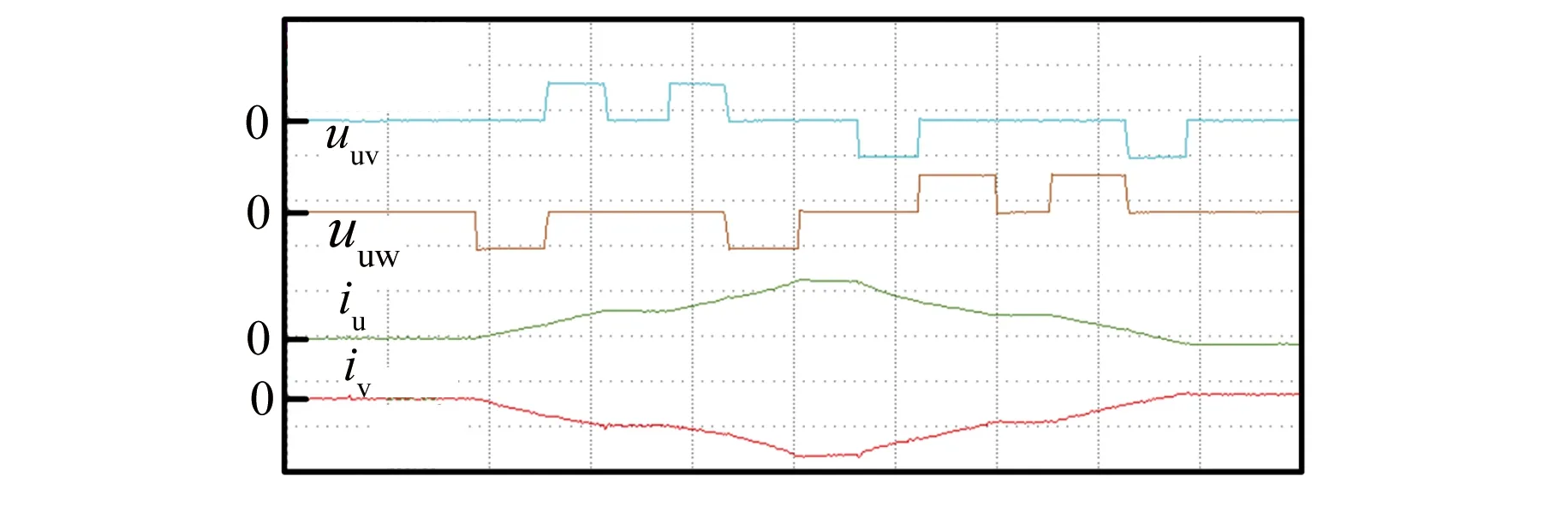
图12 转子磁极极性判断过程中的电流和电压波形

图13为转子初始位置辨识过程波形，从上到下依次为转子初始位置辨识值、极性状态标志位、负向电流和正向电流。通过光DA设备将以上变量输出至录波仪DL850E上显示。从图中可以看出，转子位置初次收敛值为5.183 6 rad，因为id1(248 A)小于id2(-268 A)，极性判断状态值为1，因此需要加π处理，最终转子辨识位置为5.218 5 rad，位置误差为0.034 9 rad。

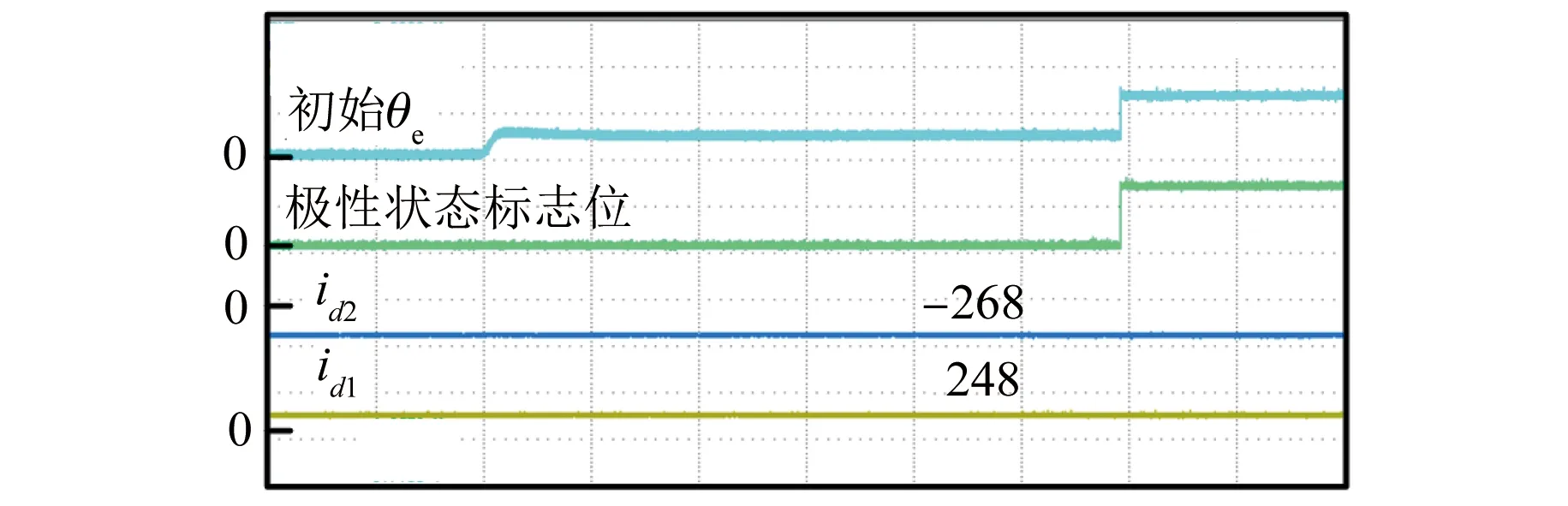
图13 转子初始位置辨识过程波形

通过手动旋转电机至下面11个位置进行转子初始位置辨识，结果如表3所示。由下表可以看出，电机实际初始位置不同时，该方法均能辨识出正确的转子位置，最大辨识误差为0.052 4 rad，平均误差0.016 1 rad。

表3 转子初始位置辨识结果 rad

4 结 语

本文在分析PMSM数学模型的基础上，采用高频方波电压注入算法获得转子的初次估计位置，然后分别在估计的d轴中注入正、反向电压窄脉冲，通过比较d轴正、反向响应电流幅值大小来判断此时定位的磁极为N极还是S极，如果定位的磁极是S极，则需要对初次估计位置进行补偿，使其定位在N极。通过Simulink仿真及试验证明，电机实际初始位置不同时，该算法均能辨识出正确的转子位置，最大辨识误差为0.052 4 rad，平均误差0.016 1 rad。