基于K-Medoids聚类的分布式光伏台区线损异常感知算法
2023-01-06梁嘉文严贝峰景楷楠李婷婷屈志原王伟宁
梁嘉文, 严贝峰, 景楷楠, 李婷婷, 屈志原, 王伟宁
(国网甘肃省电力公司甘南供电公司,甘肃 甘南 747000)
0 引 言
分布式光伏为分散建设,可减少对公共电网的影响和危害[1-4]。但随着分布式光伏数量的增加,大量的线损情况也同时出现,对分布式光伏的使用产生很大影响。若无法及时发现故障则会导致更多的问题,影响电网的稳定性、安全性。因此分布式台区线损异常程度感知对分布式光伏稳定运行有重要作用。
众多相关学者已对此展开大量研究,如陈洪涛等[5]根据K-Means聚类算法判断线损异常,但该方法无法剔除影响线损异常的孤立点,且存在应用过程复杂的问题。张裕等[6]结合多元线性回归和K-Means聚类算法进行了台区线损数据异常的检测,此方法运算简单,容易实现,可收缩性高,但运算开销比较大。
K-Medoids聚类是K-Means的改进算法,可更精准地进行数据检测。因此本文提出基于K-Medoids聚类的分布式光伏台区线损异常感知算法,完成对分布式光伏线损异常数据的检测。
1 分布式光伏台区线损异常感知算法
1.1 线损数据聚类算法
采用K-Means聚类算法聚类分布式光伏台区线损数据时,会出现聚类线损结果差异小的情况,且对噪声和孤立点比较敏感[7]。因此提出用中心点对象替换K-Means聚类算法中重心点的K-Medoids聚类算法。
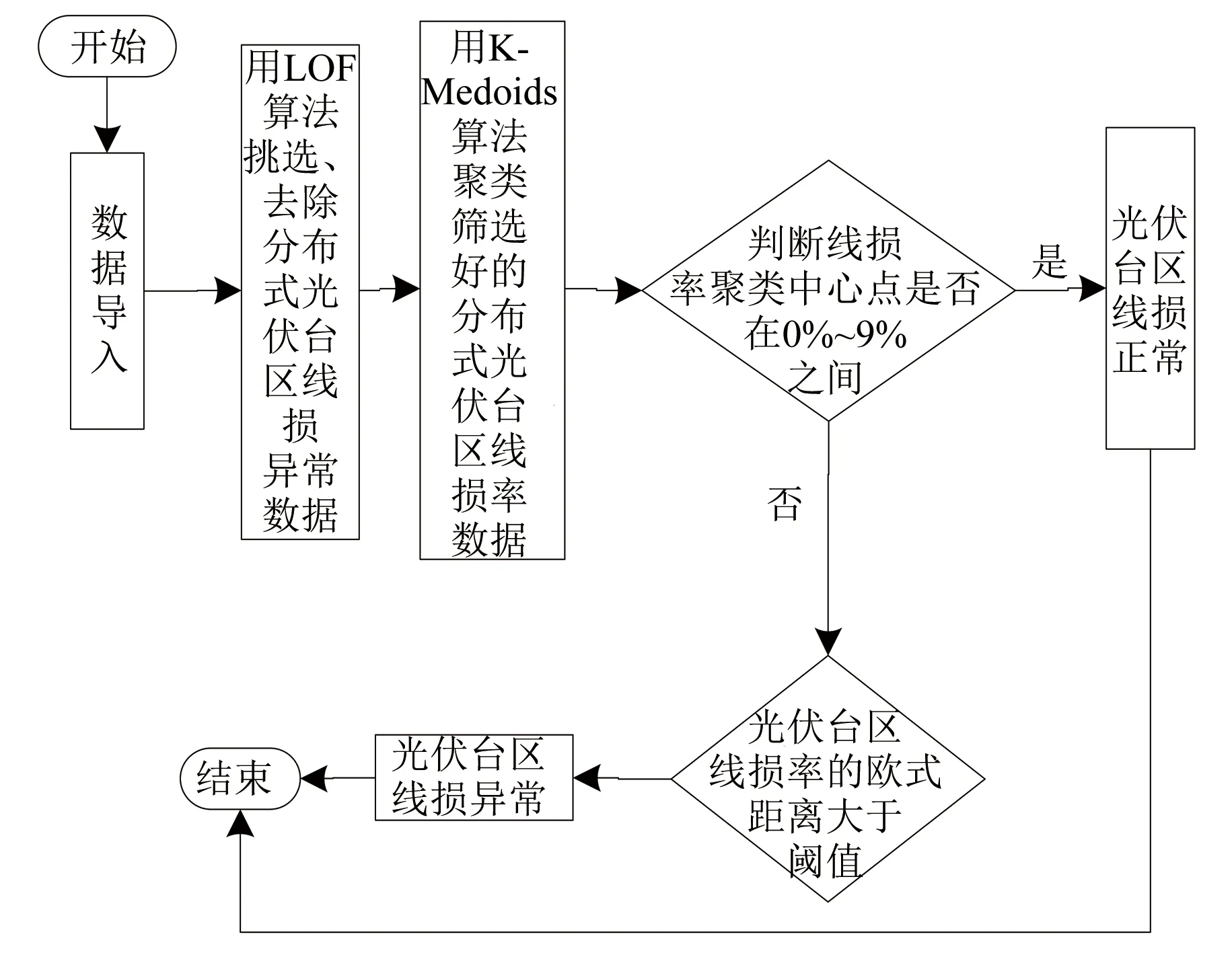
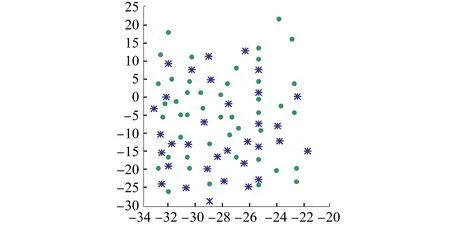
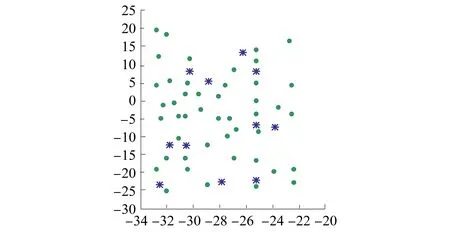
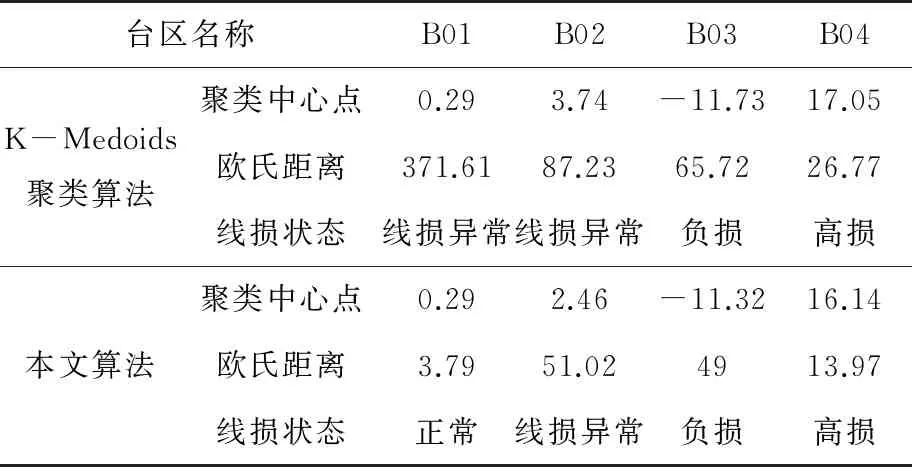
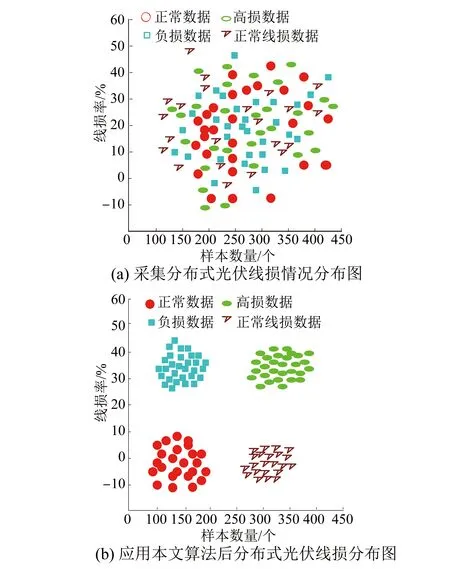
K-Medoids聚类算法的核心是已知分布式光伏台区线损数据集包括n个分布式光伏台区线损数据对象,将这些数据集分为k个聚类,将Oi作为原始簇中心,随机获取差异数据对象时,应在k聚类内完成。为了给与各数据对象距离最近的簇中分配合理的对象[8],需要基于这些数据对象到Oi的距离进行分配。顺序采集非簇中心点的数据对象Otmp的工作,需要在各簇中完成。Etmp为消耗代价,用于描述Oi被Otmp代替过程所产生的分布式光伏台区线损数据聚类成本。Ei是线损数据聚类采用Oi过程中形成的聚类成本。对比Etmp和Ei两种聚类成本,获取聚类准则函数为若Etmp 为了使簇内以及簇间的数据对象尽可能地相似以及不相似,需要对聚类准则函数可否收敛进行判断。 K-Medoids聚类算法利用欧氏距离权衡类内相似性,用下式描述该距离d(x,y): (1) 式中:x=(x1,x2,…,xp)与y=(y1,y2,…,yp)分别为数据集中两个p维的数据对象。 通过目标函数(误差平方和准则函数)E评价K-Medoids的划分聚类效果[9],则有: (2) 式中:k为聚类数量;|xj-oi|2与oi分别为欧氏距离与簇类Ci的中心点;E为数据对象与其所在簇类的中心点误差平方和。 假定待聚类数据集是n个台区线损数据对象构建的数据集合X=(x1,x2,…,xn),p维数据对象用xi=(xi1,xi2,…,xip)描述。为了得到数值最小化的目标函数E,需要得到X的一个划分数据对象Pk={C1,C2,...,Ck},确保式(2)值最小化。 K-Medoids聚类算法模型为,输入:分布式光伏台区线损数据集X,其由n个线损数据对象组成,待划分的聚类数为k;输出:k个聚类簇Ci,确保聚类准则函数E值最小化。具体步骤如下: (1) 设置初始簇中心Oi时,需要有n个数据对象组成数据集,将这些数据集分为k个聚类,在k聚类中随意选择不同的数据对象; (2) 重复迭代; (3) 为了向各数据对象距离最近的簇中分配合理的对象,需要根据式(1)计算获取的数据对象到Oi的距离进行分配; (4) 根据式(2)计算得出聚类成本Ei; (5) 为了计算数据对象Otmp的消耗代价Etmp,需要顺序采集非簇中心点的数据对象Otmp,并在各簇中完成; (6) 若Etmp (7) 直到E值保持稳定。 本文采用K-Medoids聚类算法逐个聚类光伏台区线损数据,过程中设置聚类簇数为1个。 聚类中心点和欧氏距离对分布式光伏台区线损异常感知起着重要的作用。首先孤立点对分布式光伏台区线损聚类中心点的干扰,可以通过K-Medoids聚类算法解决,但孤立点对欧式距离的干扰不能用K-Medoids描述。因此要在挑选和去除分布式光伏台区线损异常数据之后,再进行分布式光伏台区数据聚类,异常数据即为上文的孤立点。为了正确筛选出分布式光伏台区异常数据[10],本文采用了局部异常因子(LOF)算法。 1.2.1 定义局部光伏台区异常 取分布式光伏台区线损数据随意自然数K,在数据对象xa具备以下条件时,可以用数据对象xb与数据对象xa之间的距离描述xb的K-距离,即K-distance(xb)。 (1) 最少有K个对象x′a∈D{xb},满足d(xb,x′a)≤d(xb,xa),d代表距离; (2) 最多有K-1个对象x′a∈D{xb},满足d(xb,x′a) 数据对象xb的K-距离邻域可描述为 Nk-distance(xb)={q|d(xb,q)≤K-distance(xb)} (3) 即所有数据对象与xb的距离对比,为小于等于K-distance(xb)。 xb对于对象xa的可达距离表达为 reach-distk(xb,xa)=max{k-distance(xb),d(xb,xa)} (4) 对象xb与其MinPts-领域的平均可达距离的倒数为对象xb的局部可达密度,即: (5) 根据式(3)描述出分布式光伏线损LOF为 (6) 以上算法说明分布式光伏台区线损LOF与数据异常的可能性成正比,分布式光伏台区线损数据对象xb异常的程度可以用数据对象xb的异常因子描述。 1.2.2 LOF计算 n个分布式光伏台区线损数据对象组成分布式光伏台区线损数据库X,用邻域中数据对象的最小个数MinPts来计算所有分布式光伏台区线损数据对象的LOF值[11-12],此计算有两步。 (1) 为了得到各个分布式光伏台区线损数据对象的MinPts-邻域到各个分布式光伏台区线损数据对象的距离,需要使分布式光伏台区线损数据对象的MinPts-邻域在分布式光伏台区线损数据库中构成,在物化数据库导入计算结果,且使用的方法随差异维数而变化。 (2) 对不同数据对象的局部可达密度以及LOF进行运算,将各个分布式光伏台区线损数据对象的LOF值根据物化数据库M来描述。 用下式描述对象xb的局部可达密度: (7) 式中:dist(xb,xa)与|N(xb)|分别为xb和xa的n维欧式距离与xb的邻域中邻居的数目。 为了得到xb的局部偏离指数,需要满足|N(xb)| (8) LOF算法分析数据异常的标准是数据对象全部邻居的局部可达密度均值。 本文所提方法先由LOF算法对分布式光伏每日线损率的数据进行选择,再由K-Medoids聚类算法聚类处理后的线损数据,完成分布式光伏台区线损异常感知。分布式光伏台区线损率分为正常、高损和负损。正常的线损率值在0%~9%之间,高损的线损率值大于9%,负损的线损率值小于0%。分布式光伏线损的电量和数据的采集必须在智能表100%覆盖的台区进行,才能精准判断日线损率,在非智能表下的光伏台区采集数据是无效的。根据本文所提方法的思想得到了如图1所示的分布式光伏台区线损异常感知的流程图。 图1 K-Medoids算法分布式光伏台区线损异常感知流程图 导入分布式光伏台区线损数据,用LOF算法挑选和去除分布式光伏线损异常数据后,利用K-Medoids算法对LOF算法处理后的分布式光伏台区线损率数据进行聚类。在聚类时,影响分布式光伏台区线损异常的因素有两个[13],分别是聚类中心点和欧氏距离,其分别代表分布式台区线损异常的程度以及每日线损率的上下幅度。为了准确判定分布式光伏台区线损,采用光伏台区日线损率总个数与欧式距离结果的倒数描述测验中的欧氏距离数据差异。如果分布式光伏台区线损出现异常[14-15],说明日线损率上下幅度大,且欧氏距离比阈值大;反之分布式光伏台区线损正常,日线损率上下幅度较平稳,且数值在聚类中心点区间内。 利用K-Medoids算法进行光伏台区线损数据聚类分析,某种程度上可以理解为在全部可能的粒度集内得出最佳粒度值。因此为了达到K-Medoids算法的最佳数据聚类效果,引入粒度计算。 论域U以及属性集合A构成聚类空间,聚类空间T=(U,A)的相似度F(xi,xj)用下式描述: (9) 式中:|A|以及xil,xjl分别为聚类属性集合个数以及xi,xj的第l属性值;wi为聚类属性分辨能力,如式(10)所示: (10) 式中:|U|与e分别为数据对象的总数与划分块数。 区间块{x1,x2,…,xe}由属性l值分割获取,利用xi进行区间分割获取的数据对象个数为|xi|,h为数据对象数,对象平均相似度如下: (11) 在论域里分割h个粒子得到{X1,X2,…,Xh},第i个区间中的数据对象数目为|Xi|,Xi粒子的密度如下: (12) 该粒子h的平均密度为 (13) 设置有H个数据对象在第i个粒子中,用xi1,xi2,…,xin表示,粒子中心点Di用下式描述: (14) 粒计算的运算过程如下。 (1) 线损数据对象间相似度及平均相似度,由式(9)和式(11)运算。 (3) 获取各对象类似对象序号的过程,即为依据M(i,j)处理各对象获取其粗粒集G的过程,粒子即为对象及其所有类似对象构成的集合。 (4) 各个粒子的密度以及G的平均密度由式(12)和式(13)描述,有效粒子集I包含gd(xi)≥GD的有效粒子。 (5)I内各个粒子的中心根据式(14)运算,在X中录入两个随意粒子间的欧式距离。 (6) 首个聚类中心点o1是I内最大密度粒子Q1的中心点,第二个聚类中心点o2是与Q1最远的密度最大粒子Q2的中心点,由X对其余粒子的中心点到o1,o2,…,on的距离进行运算,得di1,di2,…,din,取其di最小值,求di最大值,粒子Qi的中心是oi,同理粒子Qk的中心是ok。 以簇的数量K以及n个对象的数据集为输入,得到K个簇类中心和聚类准确度。粒计算算法模型如下。 (1) 记录中心点对应的粒子是Q1,Q2,…,Qk,且K个簇类中心o1,o2,…,ok通过粒计算改进的K-Medoids聚类算法被初始化。 (2) 为距离数据对象最近的中心点的簇分配其余数据对象,并将该簇记作w,对S(w)进行运算。 (3) 分别选取在Q1,Q2,…,Qk里的非代表对象orandom,将oi用orandom替换,再更新各个簇内中心点并重新聚类,将新的簇记作w′,运算S(w′)。 (4) 运算ΔS=S(w′)-S(w),如果ΔS>0,则oi、w被orandom、w′替换,反之保持不变。 (5) 反复运算步骤(3)和步骤(4),当簇集合中对象保持稳定时,运算结束。 以某地区689个分布式光伏台区的线损数据为试验对象,验证本文所提算法的有效性。本文采用LOF算法检测和去除分布式线损异常数据,统计LOF算法不同取值下的分布式台区线损数据分布图,结果如图2和图3所示。 图2 LOF=0.4时分布式台区线损数据分布图 图3 LOF=1时分布式台区线损数据分布图 图2和图3中,圆圈代表分布式光伏台区线损正常数据,星号代表分布式光伏异常数据。当LOF值为0.4时,分布式光伏线损的异常数据数量很多,当LOF值为1时,分布式光伏线损的异常数据大幅减少。由此说明,LOF值越大对由孤立点导致的分布式光伏台区暂态异常数据的挑选和去除效果越好,能够更精准地衡量数据的异常程度,为应用K-Medoids算法进行分布式光伏台区线损异常数据感知提供更好数据基础。 利用K-Medoids算法对分布式光伏台区线损率进行聚类,设置欧氏距离的阈值为9。本文从689个分布式光伏台区中,选取4个光伏台区15天内的每日线损率,如表1所示。 表1 4个分布式光伏台区每日线损率 % 将以上分布式台区线损率,分别通过K-Medoids聚类算法、本文算法进行线损异常感知,得到如表2所示的统计结果。 表2 线损数据感知结果对比 由表2可知,K-Medoids算法将正常光伏台区数据判定为异常光伏台区,存在判定错误的缺点。本文所提算法有效结合了LOF算法和K-Medoids聚类算法,合理地避免了由孤立点导致的分布式光伏台区出现暂态异常数据对异常感知结果的影响,可以准确感知分布式光伏台区线损异常。 通过本文所提算法进行分布式光伏台区的异常线损感知。先由LOF算法对分布式光伏每日线损率的数据进行选择,如图4(a)所示;再由K-Medoids聚类算法聚类处理后的线损数据,如图4(b)所示,最终完成分布式光伏台区线损异常感知。 图4 异常线损感知效果图 图4(a)中分布式光伏台区线损的正常数据、高损数据、负损数据、正常线损数据每个类别比较分散,无法准确对数据进行感知,而在图4(b)中能清楚看到,每个数据都被聚类在各个数据的类别里,说明本文所提算法可有效、准确地解决分布式光伏台区线损异常感知的问题。 本文所提算法将LOF与K-Medoids算法结合,根据分布式光伏台区线损异常的情况,对光伏台区数据进行采样、筛选、识别,将异常数据进行聚类,保证算法能够准确地感知分布式光伏台区异常数据,并将分布式光伏的异常情况进行聚类。创新性地引入粒度计算优化K-Medoids算法,在全部可能粒度集内得出最佳粒度值,以此达到K-Medoids算法的最佳数据聚类效果,确保分布式光伏台区异常数据感知的精准性、可靠性。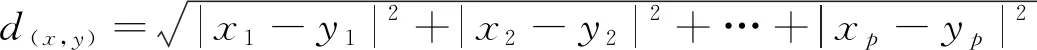
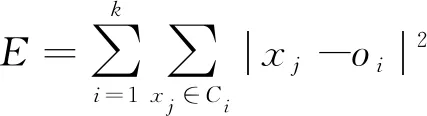
1.2 异常数据挑选和去除
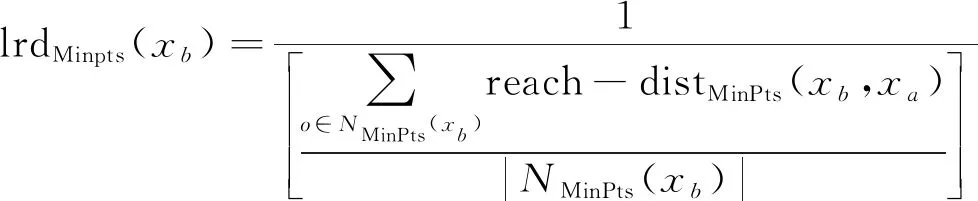
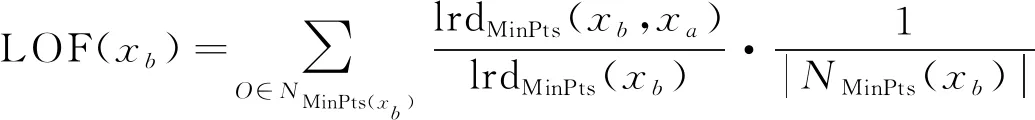
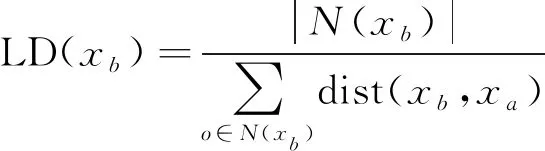
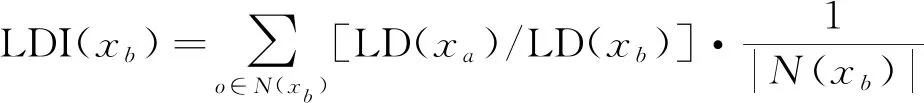
1.3 分布式光伏台区线损异常感知流程
1.4 引入粒度计算的K-Medoids算法优化
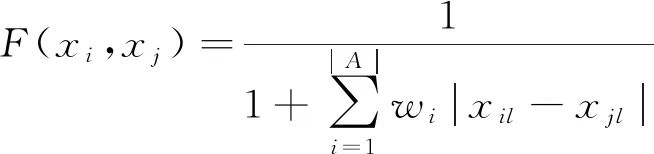
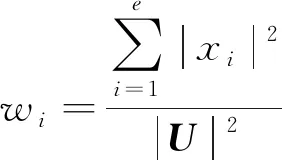
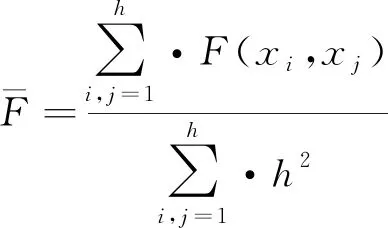
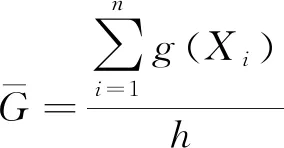
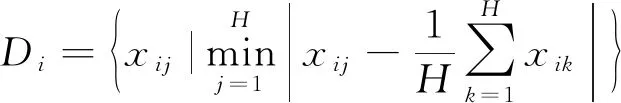
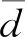
2 试验分析
3 结 语
