永磁同步电机标幺化无权重系数模型预测转矩控制*
2023-01-06李耀华张鑫泉崔康柬徐志雄兰奋龙
李耀华, 张鑫泉, 崔康柬, 陈 昕, 徐志雄, 兰奋龙
(长安大学 汽车学院,陕西 西安 710064)
0 引 言
模型预测转矩控制(MPTC)性能优越,可用于线性或非线性的控制对象,采用成本函数即可轻易实现多目标控制和非线性环节,近年来在永磁同步电机(PMSM)控制领域得到高度关注[1-5]。
成本函数作为评价备选电压矢量控制性能的方法,可以统一多控制目标,实现多目标优化控制。当控制目标为同一量纲,可直接相加,如模型预测电流控制中的定子电流d、q轴分量。但如果控制目标的量纲并不相同,则需设置权重系数,如MPTC中的磁链和转矩。但是成本函数灵活柔性的特点也带来了权重系数的设计与调整问题。权重系数大多采用试验法确定,过程相对繁琐[6]。文献[7-9]采用模糊控制动态设定权重系数,但模糊控制规则的设计较为复杂。文献[10-12]采用粒子群算法和神经网络算法实现权重系数的自整定,但需要构造大量训练数据集,计算量较大。文献[13-14]将不同控制变量转换为各自成本函数的排序位次,从而消除量纲,无需权重系数,但将成本函数寻最优转换为排序,增加了排序计算量。文献[15-16]将磁链和转矩转换为相对误差率,从而统一量纲,消除权重系数,但如果控制目标的参考值不确定,则该方法失效,仍需设计权重系数。文献[17-18]提出将磁链和转矩标幺化以消除量纲,从而消除无权重系数。
本文建立基于标幺化成本函数的表面式PMSM MPTC,仿真验证其有效性,并指出标幺化成本函数统一控制目标的变化范围,仅适用于控制目标重要性基本相同的领域,且算法实时性有所降低。
1 PMSM MPTC
定子坐标系下,表面式PMSM定子磁链矢量与转矩预测模型如下所示:
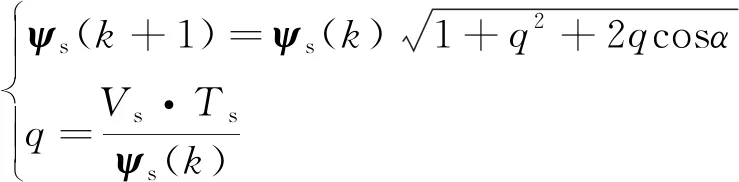
(1)
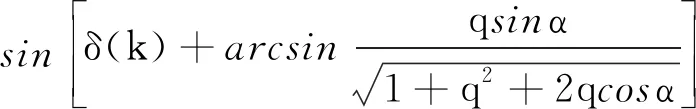
(2)
式中:ψs(k)、δ(k)和Te(k)分别为k时刻的定子磁链矢量、转矩角和电磁转矩;ψs(k+1)、δ(k+1)和Te(k+1)分别为k+1时刻的定子磁链矢量、转矩角和电磁转矩;Vs为施加电压矢量幅值;α为施加电压矢量与定子磁链的夹角[19];p为极对数;Ts为采样时间;ψf为转子磁链。
两电平三相逆变器可产生7个备选电压矢量,如式(3)所示,其中零电压矢量可由开关状态000或111生成,具体选择以开关次数最小为原则[20]。
Vs∈{V0,V1,V2,V3,V4,V5,V6}
(3)
定义成本函数如下所示:
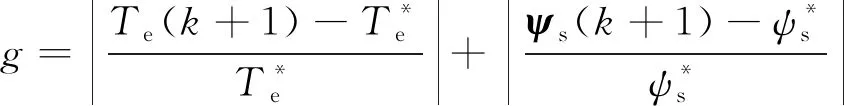
(4)
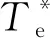
PMSM模型预测转矩系统框图如图1所示。
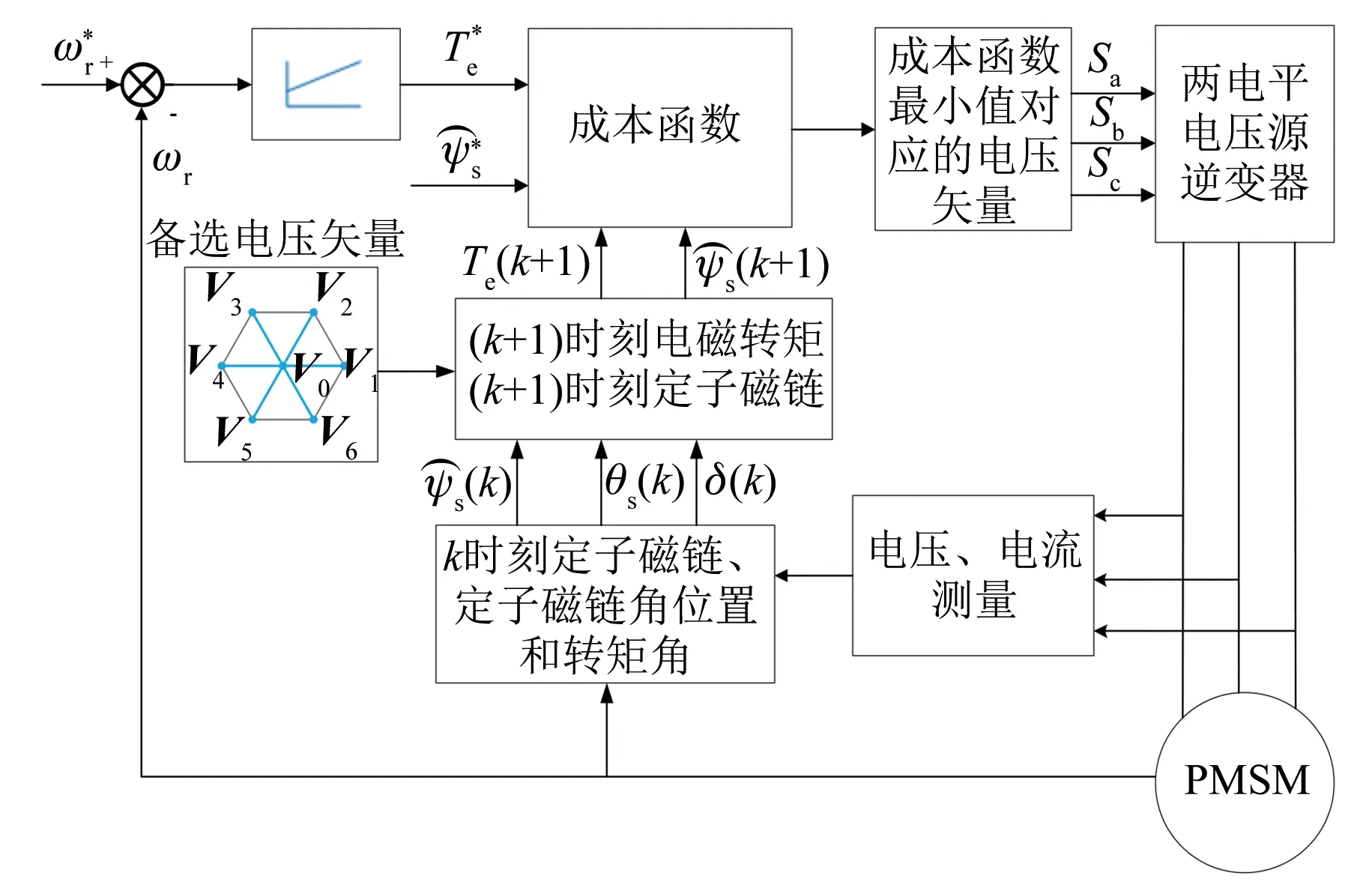
图1 PMSM模型预测转矩系统
在MATLAB/Simulink中建立基于定子坐标系的表面式PMSM MPTC仿真模型,成本函数如式(1)所示。仿真模型为离散模型,采样时间为5×10-5s,直流母线电压为312 V,初始参考转速为500 r/min,2 s时阶跃至-500 r/min,负载转矩初始为10 N·m,1 s时阶跃至-10 N·m,3 s时阶跃至10 N·m,仿真总时长为4 s。PMSM MPTC系统仿真参数如表1所示。电机系统仿真波形如图2~图5所示。
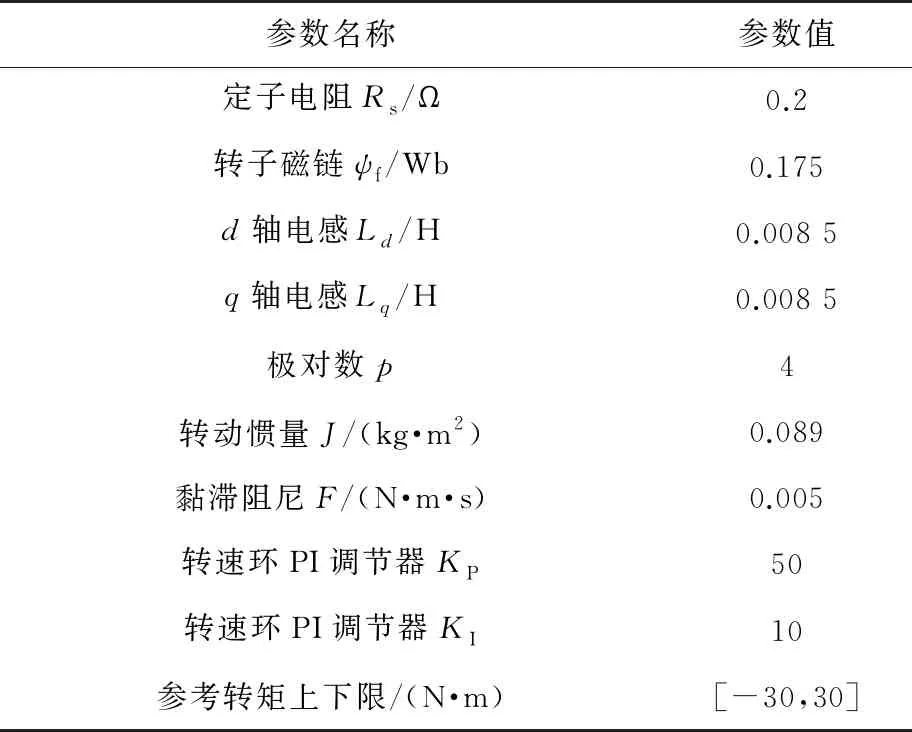
表1 仿真系统参数
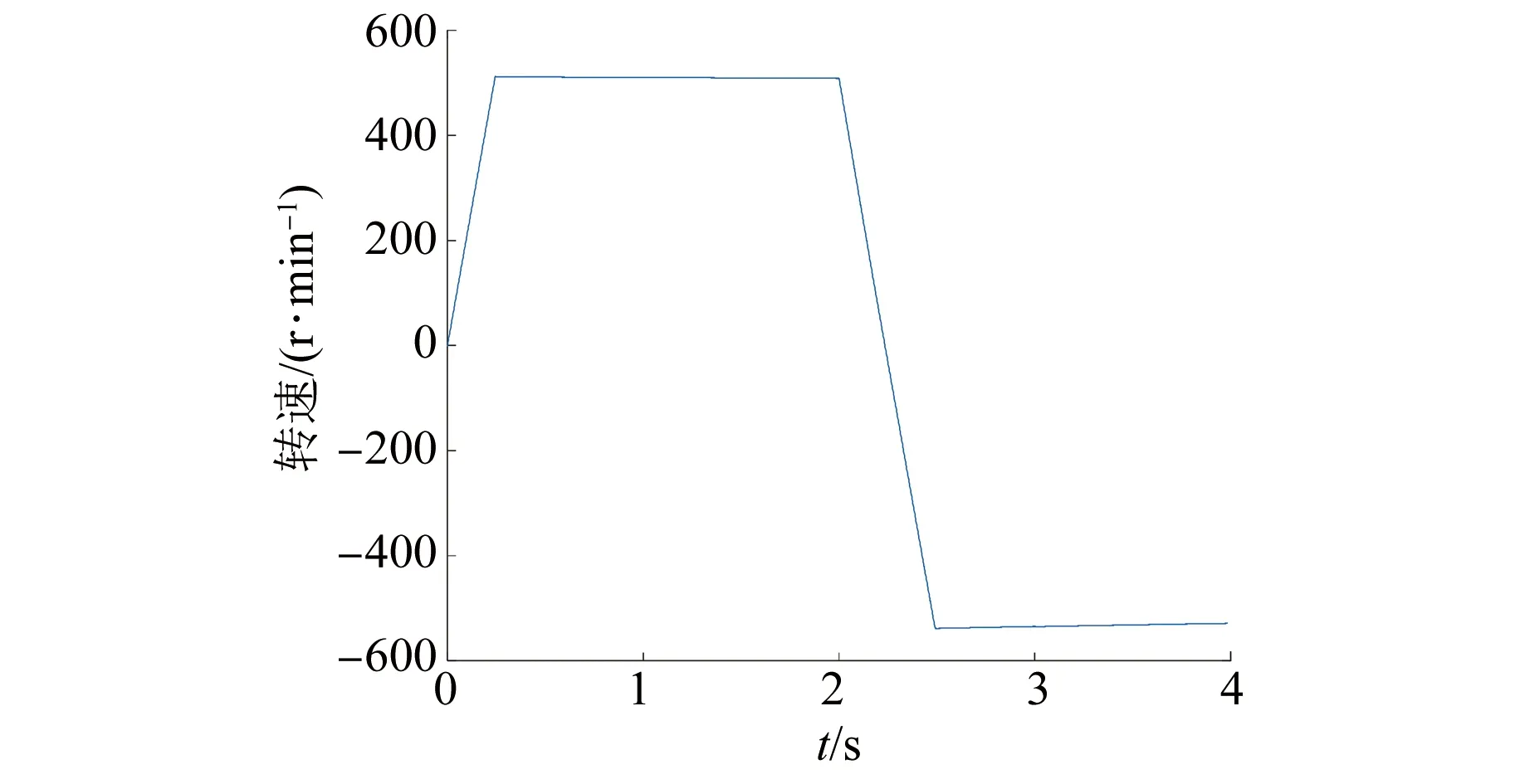
图2 PMSM转速
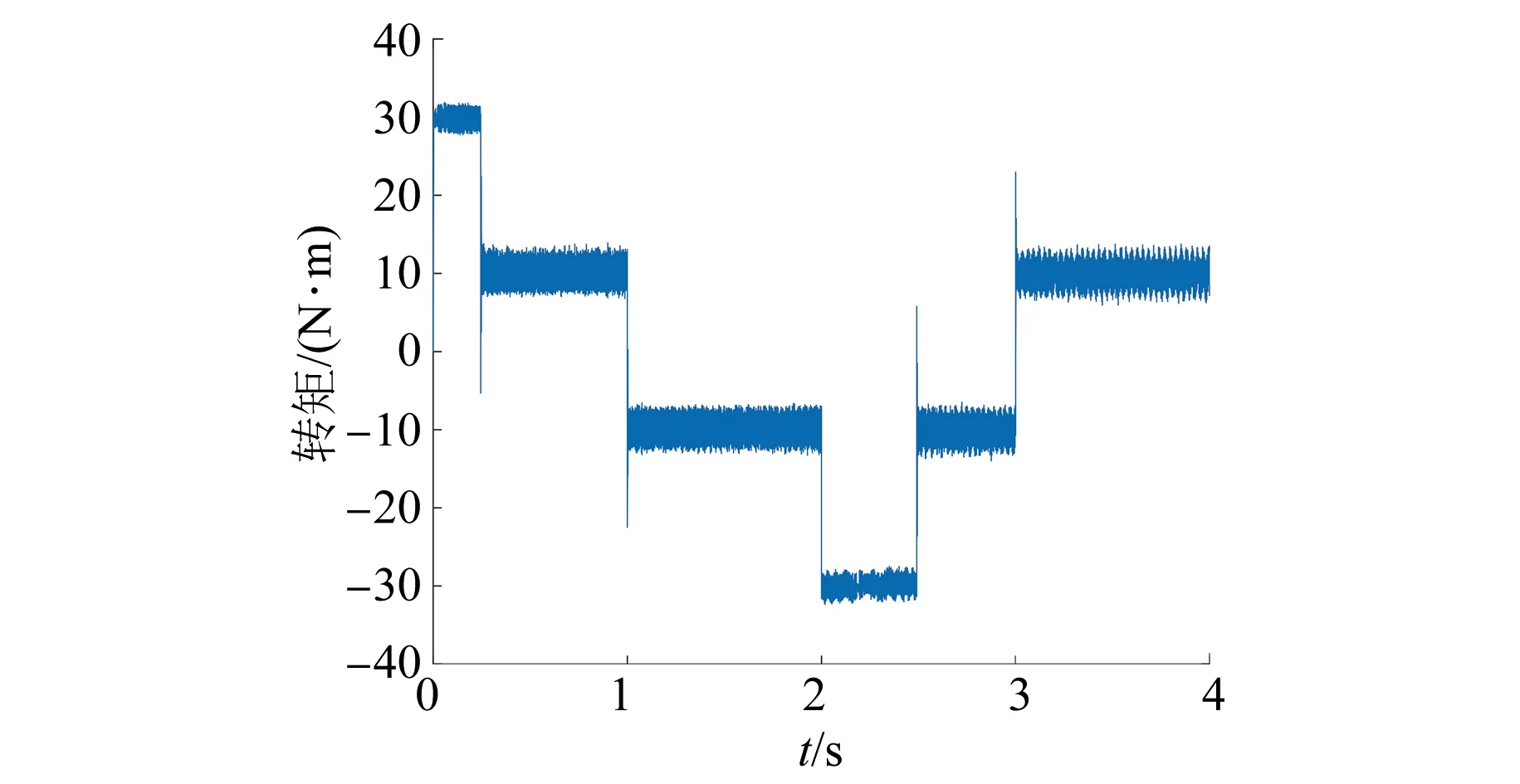
图3 PMSM转矩
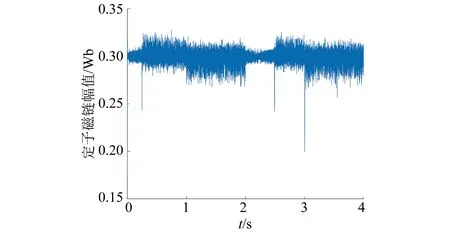
图4 PMSM定子磁链幅值
定义转矩脉动均方根误差(RMSE)、磁链脉动RMSE和平均开关频率如下所示:
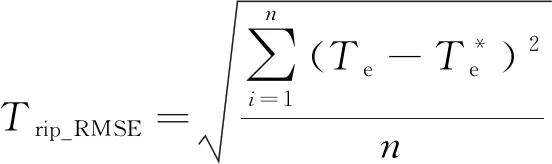
(5)
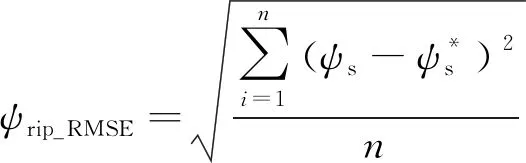
(6)
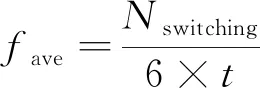
(7)
式中:n为采样个数;Nswitching为逆变器上下桥臂开关总次数;t为仿真总时长。
基于式(4)所示的PMSM MPTC系统性能如表2所示。

表2 PMSM MPTC系统性能
2 标幺化无权重系数成本函数
式(4)所示的成本函数将转矩误差和磁链误差转换为误差率,从而统一量纲,但需要转矩和磁链参考值,对于开关次数控制等没有参考值的控制目标,误差率成本函数失效。标幺化法将转矩控制误差和磁链控制误差统一转换为无量纲的标幺值,无需参考值,应用范围广。定义转矩控制和磁链控制的成本函数分别如下所示:

(8)

(9)
令gTe和gψs最大值与最小值分别为gTe_max、gTe_min、gψs_max、gψs_min,则标幺化的gTe_per-unit和gψs_per-unit如下所示:
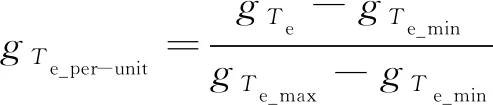
(10)
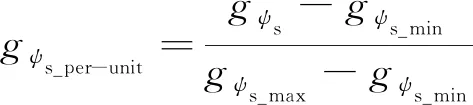
(11)
由式(10)和式(11)可知,标幺化gTe_per-unit和gψs_per-unit为同一数量级无量纲变量,变化范围均为[0,1],可消除成本函数中的权重系数,如式(12)所示:
g=gTe_per-unit+gψs_per-unit
(12)
基于上文仿真模型,采用标幺化成本函数,电机系统仿真波形如图5~图7所示,控制性能如表3所示。
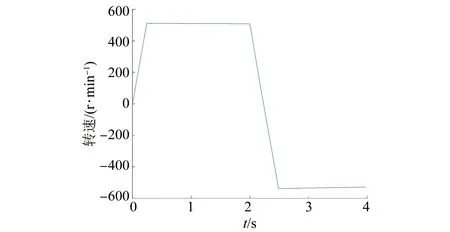
图5 PMSM转速
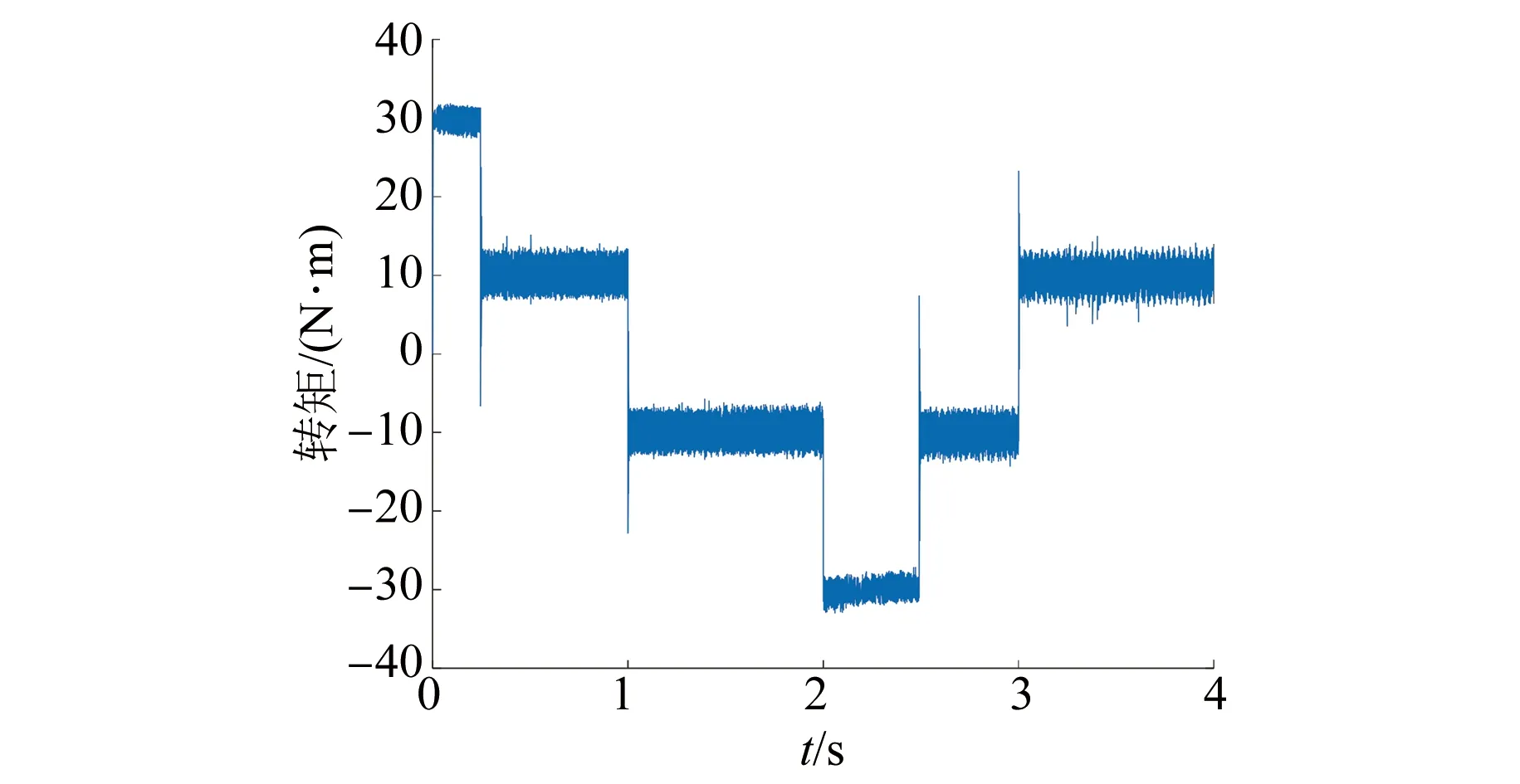
图6 PMSM转矩
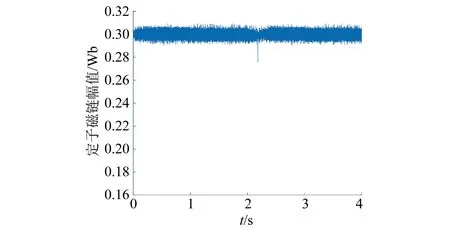
图7 PMSM定子磁链幅值

表3 PMSM MPTC系统性能
仿真结果表明,标幺化成本函数无需权重系数,此时电机可实现四象限运行,且运行良好。与误差率成本函数仿真结果对比可知,标幺化成本函数使转矩控制和磁链控制的重要性相同,弱化转矩控制,强化磁链控制,使转矩脉动增大,磁链脉动减小。
3 实时性验证
基于误差率成本函数的PMSM MPTC计算量为遍历电压矢量计算下一时刻转矩7次,计算转矩误差率绝对值7次,遍历电压矢量计算下一时刻磁链7次,计算磁链误差率绝对值7次,计算成本函数7次,7个成本函数寻最小计算1次。基于标幺化成本函数的PMSM MPTC计算量为遍历电压矢量计算下一时刻转矩7次,计算转矩误差绝对值7次,7个转矩误差绝对值寻最小计算1次,寻最大计算1次,转矩标幺化计算7次,遍历电压矢量计算下一时刻磁链7次,计算磁链误差绝对值7次,7个磁链误差绝对值寻最小计算1次,寻最大计算1次,磁链标幺化计算7次,成本函数计算7次,7个成本函数寻最小计算1次。
标幺化无权重系数MPTC额外增加7个转矩误差绝对值寻最小计算1次,寻最大计算1次,转矩标幺化计算7次,7个磁链误差绝对值寻最小计算1次,寻最大计算1次,磁链标幺化计算7次。
基于STM32单片机平台,对不同成本函数的MPTC进行单步实时性验证。单片机实时性验证的输入数据来自仿真数据,如表4所示。

表4 单片机实时性验证输入数据
将单步算法循环80 000次,共进行10组实时试验,并计算其平均值。基于误差率和标幺化成本函数的PMSM MPTC的单步平均计算耗时如表5所示。

表5 平均计算耗时
由表5可知,标幺化成本函数增大了计算量,相比于误差率成本函数,其平均计算耗时增加38.29%。
4 考虑开关次数控制的标幺化无权重系数成本函数
将开关次数控制引入PMSM MPTC,则控制目标增加为3个。此时,误差率成本函数失效,标幺化成本函数依然有效。标幺化的开关次数控制成本函数如下所示:
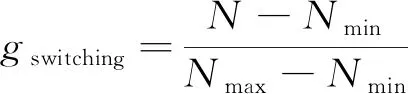
(13)
式中:N为开关切换次数;Nmax与Nmin为由当前开关状态切换到下一时刻的开关切换次数最大值与最小值。
由此可得,考虑开关次数控制的标幺化无权重系数成本函数如下所示:
g=gTe_per-unit+gψs_per-unit+gswtching
(14)
由于两电平电压源逆变器开关状态确定且有限,每个控制周期的开关切换次数也是确定的,如表6所示。
由表4和式(13)可知,开关切换次数的成本函数gswitching也为固定值,如表7所示。
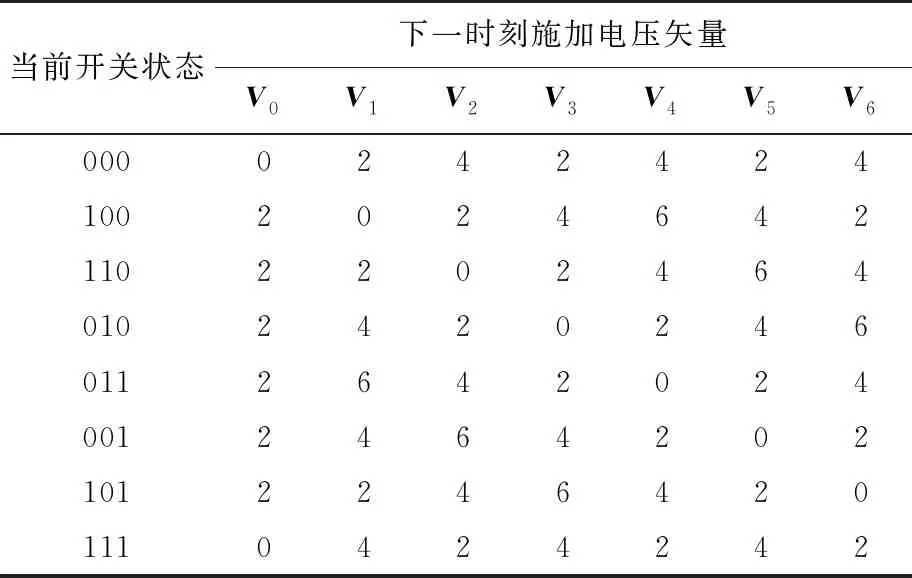
表6 开关切换次数表
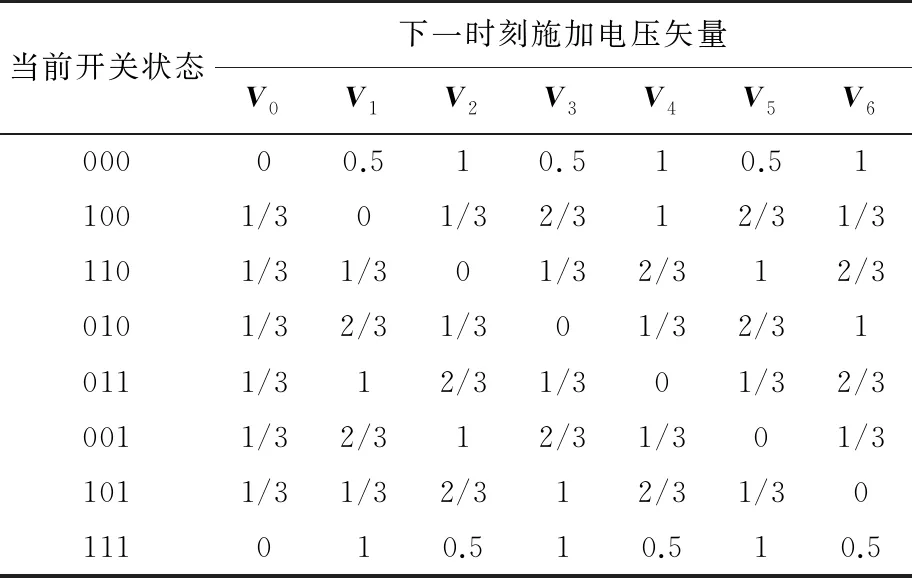
表7 开关切换次数的成本函数gswitching
基于上文仿真模型,采用标幺化成本函数,电机系统仿真波形如图8~图10所示,控制性能如表8所示。
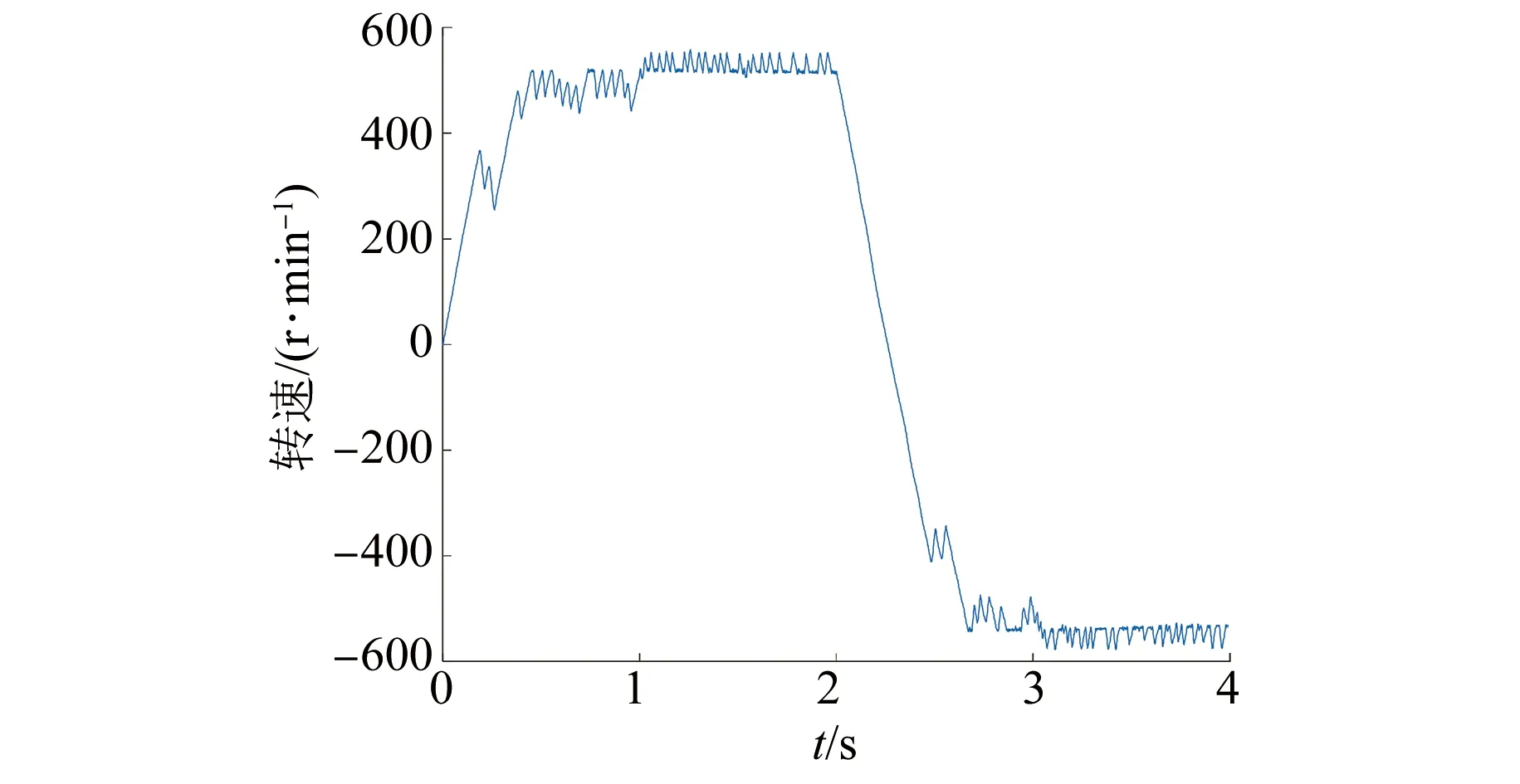
图8 PMSM转速
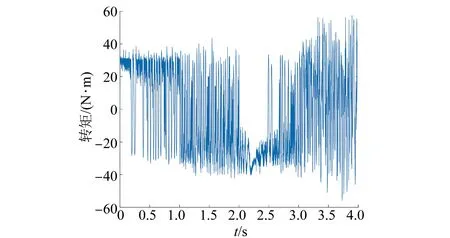
图9 PMSM转矩
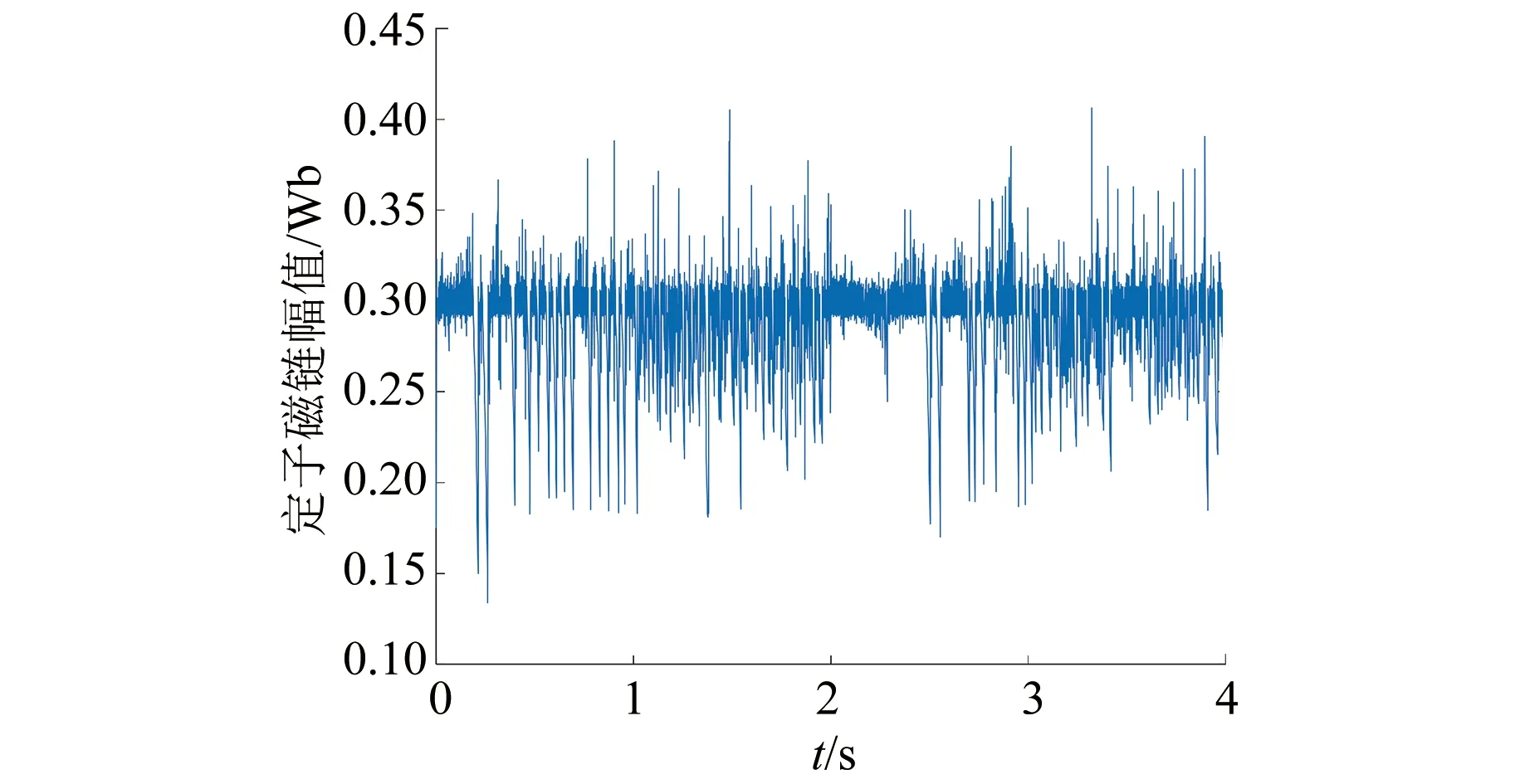
图10 PMSM定子磁链幅值

表8 PMSM MPTC系统性能
仿真结果表明,此时开关频率较低,但转矩和磁链脉动极大。这是由于标幺化成本函数在统一量纲、消除权重系数的同时,也统一了磁链、转矩和开关次数三者的数量级,使得三者的控制重要性相同。但实际电机系统的重要性排序为转矩控制>磁链控制>开关次数控制。因此,标幺化成本函数弱化转矩控制和磁链控制,产生较大的转矩和磁链脉动。为了解决上述问题,需要降低开关切换次数的重要性,对gswitching一项增加权重系数λ,如下所示:
g=gTe_per-unit+gψs_per-unit+λ·gswtching
(15)
式中:λ变化范围为[0,1]。
基于式(15)所示的成本函数,在不同权重系数下的PMSM MPTC系统性能如表9所示。
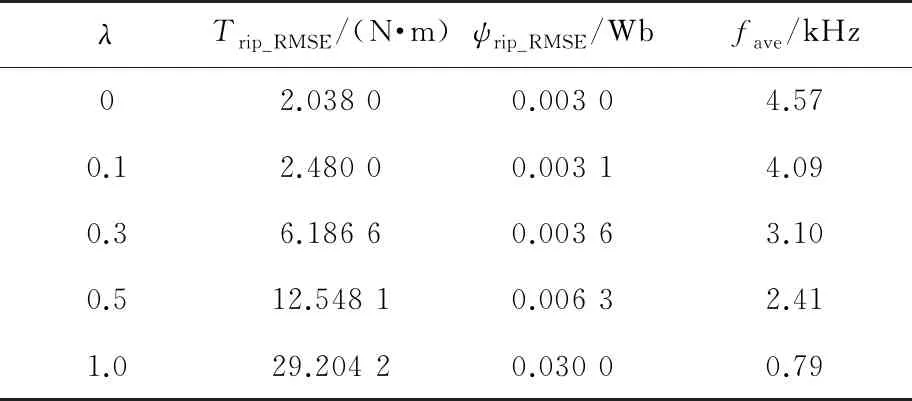
表9 PMSM MPTC系统性能
表9说明可通过增加开关次数控制的权重系数来减小转矩和磁链脉动,但这又引入权重系数。
5 结 语
标幺化成本函数在消除控制变量量纲的同时,也统一了控制变量的变化范围,所有控制目标的重要性均相同。对于MPTC的转矩控制和磁链控制,标幺化成本函数方法有效,电机系统运行正常,但其强化磁链控制,弱化转矩控制,使得转矩脉动有所增大。且标幺化成本函数增加计算量,算法实时性有所降低。
当控制目标含重要性较弱的开关次数控制时,标幺化成本函数使控制目标的重要性完全一致,电机系统过多考虑开关次数控制,电机控制性能下降。因此,标幺化成本函数仅适用于所有控制目标重要性基本相同的领域。可通过增加开关次数控制的权重系数来减小转矩和磁链脉动,但需要设计和调整权重系数。
