巧添“辅助线” 妙解几何问题

⦿江苏省江阴市顾山中学 吴灵姿

大部分学生在学习平面几何内容时都感觉到有点难度，归根到底是在处理一些问题的过程中难以把握怎么作“辅助线”，有的问题一旦确定了辅助线的添加方法，问题就变得非常容易.文章围绕初中平面几何问题如何添加辅助线主要从四个方面做了细致分析，旨在为大家提供解决相关问题的实例研究.

1 添加“辅助线”，构造新图形

我们在解决一些几何图形问题的过程中，常常是从已知条件出发，分析条件得到某个结论，然后向未知靠拢.但是在一些问题的分析中，却很难将已知与未知联系起来，这就需要我们适当添加“辅助线”，构造新的几何图形，建立桥梁关系，将待解问题转化为可解问题.下面笔者结合具体案例浅淡下对作辅助线的几点认识.

例1(2022南京)如图1，将平行四边形ABCD绕点A逆时针旋转到平行四边形AB′C′D′的位置，使点B′落在BC上，B′C′与CD交于点E．若AB=3，BC=4，BB′=1，求CE的长．

图1

根据旋转性质得AB=AB′，考虑到等腰三角形“三线合一”的性质，如图2，作辅助线AM⊥BB′，垂足为M，过点B作BN⊥AB′于点N，再计算CE的长.围绕CE构造直角三角形，过点E作EG⊥BC，交BC的延长线于点G，从而根据已知条件可以得到△AMB∽△EGC，△ANB∽△B′GE，最后根据已知边长求得答案.

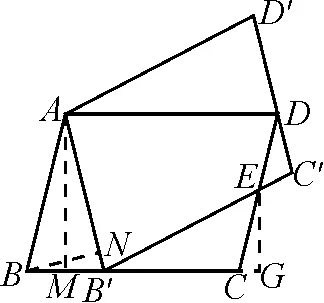
图2

2 巧用“辅助线”，构造全等三角形

对于关键已知条件，如“中线”“中点”等，注意利用延长、平行等手段，构造全等三角形.中线问题往往可以延长，构造全等三角形，将分散的已知信息融合到同一个三角形中；中点问题往往构造中位线，利用中位线的性质得到边与边或者三角形的面积等关系.

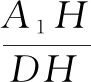
图3

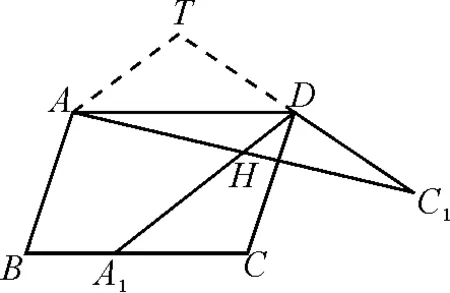
图4

3 巧作“辅助线”， 体现“平分点”

遇到关键词“平分”，对于角注意作到角两边的垂线，对于边注意作与两个端点的连线，从而构造全等形或者等腰三角形，再结合已知条件进行求解.遇到此类问题，我们往往考虑到角平分线上的点到角两边的距离相等，线段平分线上的点到线段两个端点的距离相等，此类问题涉及的内容多是求边长的问题.

例3如图5，点D在等边三角形ABC的边BC上，连接AD，线段AD的垂直平分线EF分别交边AB，AC于点E，F．当CD=2BD时，试判断AE和AF的关系．

图5

图6

4 借助“辅助线”，转化比值

遇到关键点“比值”问题，注意考虑作平行线，构造相似三角形.一般情况下，当所要求的是一个比值问题时，首先要考虑到在相似三角形中研究问题，从而确定对应线段的比值.若能明显观察到两个线段所在的三角形相似，可利用已知条件进行分析求解，但是大多问题不能直接判定相似，这就需要根据题意适当添加辅助线进行转化，从而让问题变得易解.

图7

图8

5 巧连“辅助线”，建立相似三角形

遇到关键点“切线”，注意连接圆心与切点，构造直角三角形.根据切线的定义可以很明确地判断切点与圆心连线的重要性.故在问题中出现切线必连切点与圆心，从而再构造直角三角形；其次是形如“a+kb”的最值计算，根据k的值巧妙构造相似三角形也是常见辅助线作法.

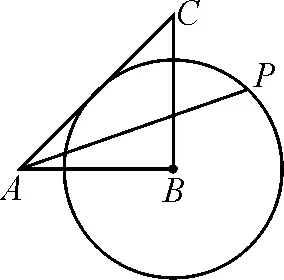
图9

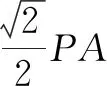
图10

当然，针对不同的问题应考虑不同的方法和思路作辅助线.如，出现面积问题，往往作底边的高线为辅助线；遇到多边形问题，往往转化为三角形，割补多边形是作辅助线的重点；出现线段之和或之差问题，采用截长或补短法作辅助线是常见之法.

在平面几何问题中，添加辅助线的方法多种多样，且灵活多变，仅借助几种方法是不够的，还需要我们准确把握相关的基本概念和基本性质，多练习多总结，在给定的条件下结合图形不断深入研究隐含的或规律性的问题，不断积累突破疑难问题的经验与方法.