基于直观想象的后建构课堂教学实践研究*
——以“反比例函数图象下的面积问题”为例
2022-04-16江苏省无锡市东绛实验学校毛巾钧
⦿江苏省无锡市东绛实验学校 毛巾钧
1 引言
《义务教育数学课程标准(2022年版)》指出,数学学科核心素养主要表现为:抽象能力、运算能力、几何直观、空间观念、推理能力、数据观念、模型观念、应用意识、创新意识.其中,利用几何直观建立形与数的联系,构建数学问题的直观模型[1].后建构课堂,是指在解构学生已有的知识,使之被学生重新认知和接受,并在新的认知情境下进行重组和再构,形成新的认知结构的课堂.后建构教学是在建构主义和后结构主义指导下,在新知识教学结束后,帮助学生建构更为完整的知识结构、技能结构、思维结构和素养结构的课堂教学[2].
笔者最近观摩了一节区公开课“利用几何直观解反比例函数图象下的面积问题”,对直观想象这一核心素养的形成和发展有了更深层的理解和体会,也借此思考并研究后建构课堂教学如何使核心素养的培育真正落地呈现,如何使学生的深度学习有效发生,如何促进高阶思维的深层发展.
2 课堂再现
2.1 课堂引入,回顾知识
问题1由如图1你能想到什么?

图1
生:这是反比例函数的图象,双曲线.
问题2你能求出这个函数的表达式吗?
生:不能.
问题3如何添加一个条件,可以求出它的表达式?
生1:给出一个具体的点,比如图象经过点A(2,3).

教师解释了所谓“几何直观”是指“我们能直接观察到的有关图形(图象)的信息”,并在以上问题串的基础上引出本节课的课题:利用几何直观解反比例函数图象下的面积问题.在教学过程中,教师逐步板书本节课复习反比例函数的主要内容,如图2.
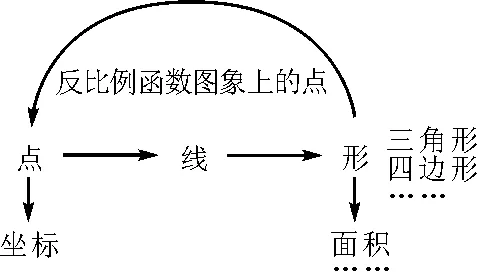
图2
2.2 回顾结论,引出模型
教师出示两个基本图形,如图3和图4,通过个别提问,让学生回顾与三角形面积有关的基本结论.

图3
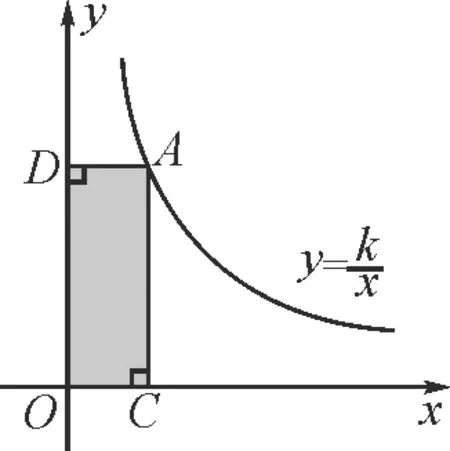
图4
模型1:一点一线.
教师出示两张变式图,如图5和图6,求阴影部分的面积.

图5

图6
在图5中,大部分学生能想到通过平行得到同底等高的两个三角形面积相等进而转化为求△OAC的面积.教师引导学生借助基本结论小结归纳此模型“在一条双曲线上取一个点,得到的三角形或四边形的面积问题”,并得出解决面积问题的方法1:平行线→等积转化→基本图形.
模型2:两点一线.
如图7和图8,增加有关图形面积的具体条件,利用基本图形解决面积和差问题.归纳此模型为:在一条双曲线上取两个点,得到的三角形和四边形的面积问题.其中四边形的面积和差问题设置了类比学习,让学生类比三角形的面积问题自己画图设问并求解.在解决问题的基础上归纳得出解决面积问题的方法2:割补法.

图7
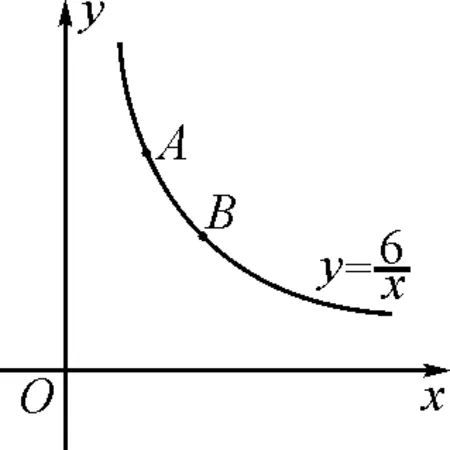
图8
模型3:两点两线.
如图9和图10,教师归纳此模型为:分别在两条双曲线上各取二个点,得到的三角形和四边形的面积问题.其中四边形的面积问题同模型2一样,设置了类比学习,让学生类比三角形的面积问题自己画图设问并求解.

图9
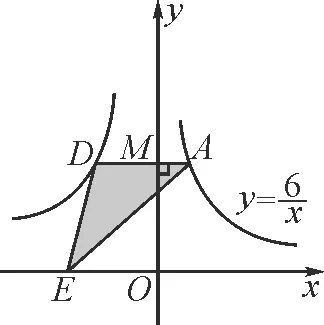
图10
2.3 综合运用,解决问题
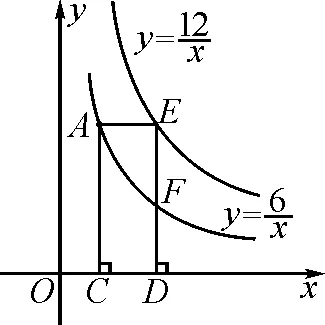
图11
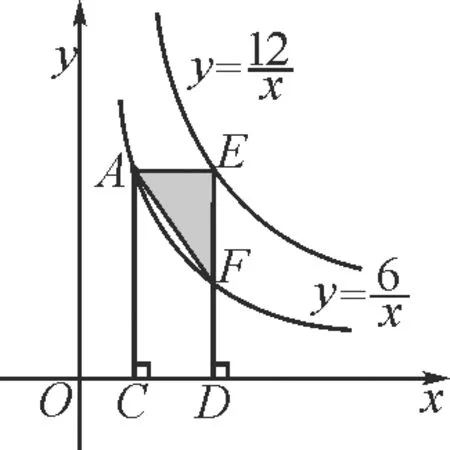
图12
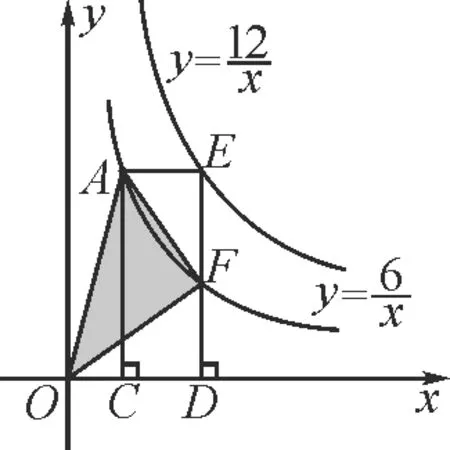
图13
2.4 总结归纳,能力提升
教师总结归纳,如表1

表1 模型归纳表
3 课后思考
3.1 直观想象引起知识的发生
笛卡尔创立的解析几何,尤其是函数图象问题,数形结合思想方法的体现最为明显.本节课全程仅用十几张图解决一系列反比例函数图象下的面积问题,充分体现了几何直观的震撼力.本节课在引入环节,从较为熟悉的一目了然的双曲线入手,唤起学生对旧知的回忆,并在此基础上引起学生对反比例函数图象中的面积问题展开深入研究.
3.2 直观想象促进知识的发展
通过直观想象,学生进一步建立形与数的联系,构建反比例函数图象下面积问题的直观模型,从模型1(一点一线)到模型2(两点一线)到模型3(两点两线),构建一系列模型,均根据基本图形来解决问题.形成的若干直观模型,可促进学生对反比函数图象下的面积问题的掌握,并能总结归纳计算面积问题的3种方法.
3.3 直观想象助力知识的运用
在综合运用环节,由直观的基本模型图再次深入探究,借助几何直观理解问题,以形助数,在具体的问题情境中形成数学直观从而运用所学知识解决问题.在求解斜三角形的面积问题时,学生能够根据几何直观利用模型结论,化复杂图形为基本图形,化未知为已知,在知识的综合运用中进一步掌握反比例函数图象的性质以及面积问题的求解.
3.4 直观想象促成知识的归纳
本节课研究反比例函数图象下的面积问题是在几何直观的大背景下展开的,从直观观察到方法提炼到思维提升,层层递进,层层落实,很好地将基本知识、基本技能、基本方法、基本思想落实到位.将零散的知识形成框架结构,方法和思想融合其中,促成学生对知识的归纳和建构,真正意义上使得核心素养落地,深度学习发生.
4 后建构再探
如何使核心素养的培养真正落地呈现,如何使学生的深度学习有效发生?借助对本节课的思考,笔者从以下三个方面对核心素养背景下的后建构课堂教学进行再探.
4.1 以素养为指向设定教学目标
后建构课堂往往承载着对知识的回顾与再构、巩固与再生.如,本节利用几何直观解反比例函数图象下的面积问题,在教学设计中融入直观想象这一核心素养,更确切地说,是将直观想象这一核心素养贯穿始终.它既是解决函数图象中面积问题的工具,又是素养的外显表现,是方法也是目标,是一以贯之的内线也是重要方法之一.不妨拓展一下,在初中阶段有关函数(一次函数、反比例函数、二次函数)的专题复习中,数形结合是重要的思想方法,而直观想象是发现、提出、分析、解决问题的重要手段,它能够有效地建立形与数的联系,利用几何图形描述问题,借助几何直观理解问题.函数问题中有关图形(图象)的问题,比如图象的交点、图象的性质、图形的周长面积、图形的存在性等都需要借助直观想象来理解并解决问题.它既是重要手段,也是理解和解决问题的基本素养.
4.2 以素养为手段制定教学模式
核心素养背景下的课堂教学模式大致分为四个环节:(1)知识梳理,(2)建立模型,(3)模型运用,(4)总结归纳.以本节课为例,首先梳理反比例函数的有关知识点,最好能形成网络框架;其次建立两个基本模型并在此基础上建立三个变式模型(一点一线、两点一线、两点两线);然后综合运用模型解决复杂问题,即通过达成度进一步检验模型;最后总结归纳模型的运用、方法的掌握、思想的渗透等.整个学习过程经历学习的发生、发展、运用到知识建构,四个环节相辅相成,呈现直观想象这一核心素养在解决问题中的中心位置.几何直观贯穿学习过程的始终,在学生的整个学习过程中尽情展开,绝不是一点一滴地渗透,而是通过一系列图形、一系列模型将几何直观这一核心素养充分呈现.从图形入手,以直观为手段,帮助学生分析和解决反比例函数图象下与比例系数有关的面积问题.
4.3 以素养为目标落实问题的解决
素养的落地呈现最终的检验标准是什么?解决问题.直观想象有助于建立形与数的联系,构建数学问题的直观模型,探索解决问题的思路.在本节课中,如果最终能增加一个解决问题的环节,也就能真正使素养落地呈现,比如解决一个实际生活中与反比例函数有关的问题(诸如八省联考中的有关大兴机场的问题).数学学习的目的是为了解决问题,尤其是解决具有生活价值的问题.我们需要让学生了解怎样的知识才是有价值的.生活和未来都充满不确定性,而确定的方法、技能、素养能够帮助学生解决这些问题,这才是最有价值和意义的.在核心素养背景下的课堂教学,要走出课堂,走进生活.解决问题是数学知识和现实生活的桥梁,而直观想象是数和形的桥梁,数形结合形成数学直观,在具体的情境中解决问题从而使得核心素养真正落地呈现.
5 结语
核心素养背景下的后建构课堂教学,在不断实践和积累中彰显它独特的魅力,使得核心素养可观测、可评价、可呈现、可落地,这样的课堂教学要形成的课堂形态、教学范式需要持续地认真探索和实践,只有这样六大核心素养才能真正意义上在课堂教学中落地,才能促进学生的深度、高效学习,促进思维的高阶发展.
