横流驻波增长因子模式在跨声速边界层的应用

王玉轩，徐家宽，*，张 扬，乔 磊，白俊强，3

(1.西北工业大学航空学院，西安 710072；2.西安交通大学机械结构强度与振动国家重点实验室，西安 710049；3.西北工业大学无人系统技术研究院，西安 710072)

0 引言

以减阻、减排为核心的“绿色航空，清洁蓝天”计划的提出使得层流设计和层流控制技术成为全球的研究热点。要进行层流设计和控制技术研究，转捩预测技术是首当其冲需要解决的难题[1]。

经过近半个世纪的研究和诸多知名研究机构关于亚跨声速边界层转捩预测的研究和实践，基于线性稳定性理论（linear stability theory,LST）的eN方法表现突出。eN方法是一种半经验的转捩预测方法，一般通过线性稳定性理论求解得到不稳定波的增长因子N在空间的分布，人为给出转捩临界N值，从而获得转捩位置。Klebanoff等[2]的研究表明小扰动环境下，边界层内扰动的T-S波线性演化区域几乎占据转捩前整个层流区域的80%左右，尽管横流波到非线性阶段饱和区域较长，但是其线性发展区域仍然占大部分区域，这是使用线性稳定性理论预测T-S波转捩和横流转捩能够成功的根基。二维边界层的eN方法于20世纪50年代被Smith[3]和Van Ingen[4]提出，在航空航天领域得到了广泛应用。该方法后来被Mack[5]和Cebeci[6]等进一步拓展至三维边界层，使得基于LST的eN方法在理论分析层面趋于完善。为了使得eN方法能够计算部分工程问题，国内外的众多知名科研机构都发展了基于传统线性稳定性理论的eN分析程序[7-10]，与CFD求解器和边界层方程等外部求解器耦合迭代从而实现线性稳定性分析。法国宇航研究中心（ONERA）[11]和德国宇航研究中心（DLR）的科研人员[12]基于多年的稳定性分析数据构造了基于线性稳定性理论的eN数据库，将该数据库与CFD求解器和边界层方程等外部求解器一起耦合求解，从而获得所需要的扰动增长因子N。

传统的基于线性稳定性理论的标准eN方法包括以下六个步骤：第一，求解精确的层流基本流；第二，对层流基本流进行速度分解和坐标变换以及法向一阶导数和二阶导数的计算；第三，猜测不稳定波可能出现的区域和参数区间，通过求解扰动波的特征值筛选不稳定波；第四，沿流线方向积分特征值获得不同扰动的增长因子（N factor）；第五，给定临界N值判定转捩位置；第六，通过固定转捩的方式给出层流区和湍流区的分布，从而计算气动力。

经过国内外知名科研机构的验证，基于线性稳定性理论的eN方法可以对工程中出现的常规气动外形表面的Tollmien-Schlichting（T-S）波转捩、层流分离泡转捩和横流不稳定性转捩进行预测，满足工程需求。这种RANS求解器与eN求解模块的迭代耦合策略在一定程度上将传统的线性稳定性理论分析推广到了比平板、翼型更为复杂的常规气动外形，在机翼、翼身组合体、升力体等构型的转捩预测中得到了广泛应用[13-14]，可以解决大部分工程问题，理论上该方法适用于任意复杂外形的转捩预测。但是，该方法实现难度较高，前后处理较为复杂。存在以下问题：第一是分析过程比较复杂，即使是数据库方法，也需要独立的转捩分析模块去单独处理线性稳定性理论的求解，然后与RANS求解器进行耦合迭代。该方法各模块的代码之间耦合性较差、复杂度高，且在并行化计算方面较难实现。对于稍微复杂的基本流求解和速度分解等都很难保证求解精度，依然需要进行积分和搜索等非当地操作，不符合RANS模式仅依赖当地变量的发展需求。第二是只能给出局部规则区域的层流-湍流分布，难以给出复杂气动外形的全机层流-湍流气动力数据，这对层流优化设计而言是非常难以接受的。第三个是对于扰动源的考虑不足，对于壁面粗糙度的影响，需要通过改变横流驻波转捩临界N值的方法加以考虑。Crouch等[15]发展的临界N值判定准则尚不具备普适性，仅由一组试验数据标定而来。

随着近年来基于RANS方程的当地化转捩模式的快速发展[16-28]，结合两者的优点，让线性稳定性理论模式化的思路逐渐涌现。1982年，Drela和Giles[29]对不同压力梯度下的层流相似性解进行了大量的线性稳定性分析，从而获得了T-S波的扰动增长因子N与形状因子和动量厚度雷诺数的直接函数映射关系。这是研究人员首次对线性稳定性理论进行简化，使得eN方法可以非常便捷地应用到翼型绕流的转捩判定当中。2013年开始，Coder和Maughmer[30]基于Drela等[29]的研究成果，首次提出了流向扰动增长因子NTS的输运模式。该模式的构造思想为：对不同压力梯度下的边界层相似速度型进行大量的变参数稳定性分析，从而提炼出N值包络线与当地形状因子和动量厚度雷诺数以及边界层特征尺度之间的函数映射关系；然后对关系式中出现的非当地变量逐一进行合理的当地化，提出新的流场识别因子，构造新的计算函数，最后与湍流模式耦合形成转捩-湍流预测模式。模式构造完成后应用非常简单便捷，与CFD求解器求解基本流一起计算，一次性求解即可获得整个气动构型的层流-湍流分布和整体的气动力等数据。随后，Coder不断对该模式进行改进，尤其是提出了满足伽利略不变性的形状因子参数[31]，使得该模式在非惯性坐标系下也不再有缺陷，整体预测性能趋于完善。但是该模式只能预测流向的T-S波转捩和层流分离泡转捩，无法对横流转捩进行预测。而航空航天飞行器表面，横流转捩现象非常突出。Coder等[32]在2020年对该方法进行了发展，将横流判据加入其中，使得该方法能够用于横流转捩的预测。但是，其对于横流的预测，采用的是Langtry等[18]通过风洞试验数据拟合出的经验关系式，没有对横流不稳定波的发展进行独立的、物理的建模。低湍流度环境被认为与高空实际飞行环境相似，在此环境下，尽管非定常横流涡的增长率更大，但是三维横流边界层流动主要由定常横流涡主导转捩[33]。因此，对于小扰动飞行环境，后掠翼表面横流定常波的分析和建模是关注的重点。为了完善这一功能，Xu等[34-35]提出了横流定常波扰动增长因子NCF输运模式，以横流强度因子和螺旋度雷诺数为根基发展了完全基于当地变量的NCF输运模式，经过广泛的低速算例验证，证实了其合理性。随后，该模式又进一步被添加了壁面温度效应修正[36]，使其可以对跨声速的部分变壁面温度算例进行预测。

本文将重点展示当地化的NCF输运模式在跨声速后掠翼流动中的公式细节和应用实例，验证其在跨声速边界层中对横流驻波扰动增长因子的预测能力，证实其合理性和可行性，进一步促进该方法的推广应用。对于eN方法与转捩经验关系模式的预测结果比较，可以参考文献[37，38]。

1 输运方程的数学描述

在包络近似方法中，唯一需要追踪的变量就是沿流动方向发展的包络增长因子N。Drela等[29]的简化模式的线性稳定性理论可使用增长因子标量输运方程来实现流场中增长因子N的求解。Coder等[30]首先通过无量纲化的当地压力梯度参数 HL=实现非当地形状因子H12的当地化计算，从而实现了整个输运方程内核公式的当地化求解。这里S是剪切应变率的模，d为流场中任意一点到壁面的最小距离，Ue是边界层边缘速度。Coder等[30]构造的Tollmien-Schlichting （T-S）不稳定波增长因子输运模式的形式为：

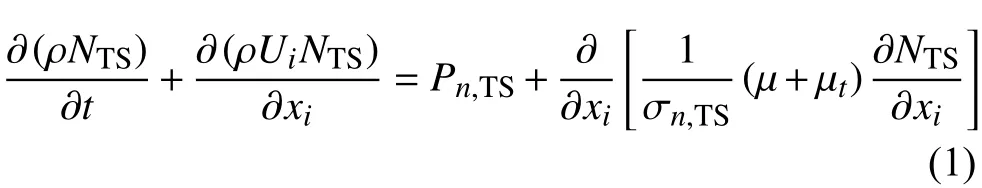
其中，扩散项系数σn,TS=1.0， Pn,TS是源项，µ是分子运动黏度系数，µt是湍流涡流黏度系数。源项是基于Drela的LST分析结果进行建模，所用到的失稳雷诺数和N因子增长斜率函数等均是流向形状因子H12的函数，具体公式信息可以参考文献[30]。

上述模式只能对流向转捩（T-S波和层流分离泡转捩）进行预测，无法预测横流转捩。本文作者基于对三维层流边界层相似性解进行的大量的线性稳定性分析结果，提出了横流驻波的扰动增长因子输运模式：

其中，扩散项系数σn,CF等于1.0，源项Pn,CF由以下几个部分组成：

式中，ρ是密度， Fonset是开关函数， NCF_growth是增长因子的发展函数和TCF是可压缩修正项目。所有函数的构造都源于对不同压力梯度和后掠角（0°～90°）下的Falkner-Skan-Cooke三维层流边界层相似性解进行的线性稳定性分析结果。

第一，开关函数的表达式为：

根据稳定性理论分析结果，起始失稳横流雷诺数RCF0是 横流形状因子 Hshape=的函数，计算公式为：

这里，Tw是壁温，Te是边界层边缘的温度。在 Hshape的定义中，dmax是 最大横流速度的高度，δCF（等于到横流速度分量变为其最大值的10%时与壁面的距离，靠近边界层边缘一侧的值）是横流特征厚度。横流雷诺数RCF定义为RCF=|wmax|，|wmax|是最大横流速度的绝对值，υe是边界层边缘的运动黏度。

关于横流雷诺数RCF的当地化，我们提出了一个新的当地指示因子该指示因子的定义不同于Grabe等[17]发展的螺旋度雷诺数然后， RCF可以通过公式（6）进行计算：

其中βH为Hartree压力梯度因子。

第二，增长因子的发展函数的计算公式是：

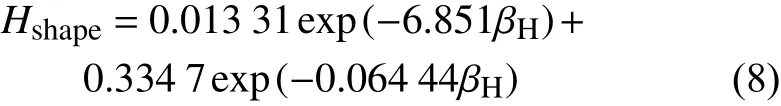
第三，可压缩修正项TCF等于其中壁面温度可以通过以下公式进行估算：

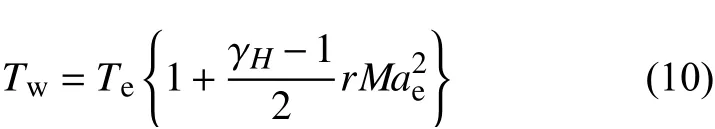
其中，r是温度恢复因子，Mae是边界层边缘马赫数、层流边界层中，r一般等于对于理想气体，且没有额外热源的情况下，边界层边缘速度Ue可以通过总焓不变关系式获得：

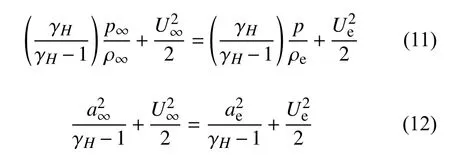
其中，γH是比热比，p是压强。边界层边缘的声速ae也可以使用类似的方法来计算。此外，ρe可以由等熵关系式ρe=给出。然后，Mae=。对于亚声速流和跨声速流，此估计方法对边界层边缘速度和马赫数的估算效果很好。

至此，模式中只有Hartree压力梯度因子βH尚未求解，该参数与Thwaites压力梯度因子λθ=有明确的函数关系βH=求解Thwaites压力梯度因子即可获得βH。Thwaites压力梯度因子λθ具体的求解方法见文献[17，36]。

有效间歇因子的触发函数表达式为：

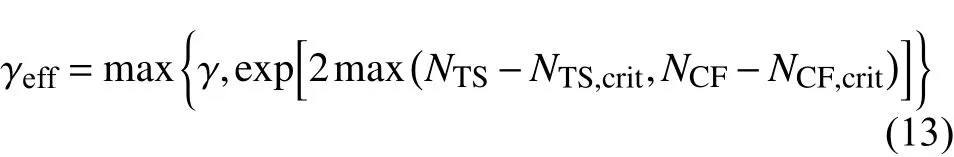
其中，γ是间歇因子，γeff是有效间歇性因子，用于触发湍流模式中的转捩现象。转捩模式与Menter的SST湍流模式之间的耦合方式如下：

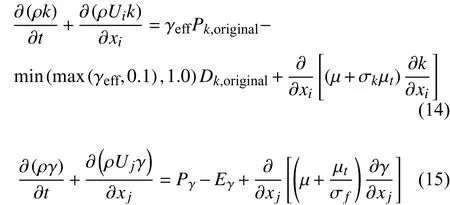
注意， γeff是通过控制湍流模式的产生源项Pk,original实现在边界层内部对层流和湍流的切换。到这里，横流驻波增长因子的输运方程已经构造完毕，所有变量均实现了当地化求解。下面将通过两个经典算例验证和分析该模式的预测能力。

2 验证和分析

本文所构建的横流驻波增长因子输运模式基于CFL3D程序进行开发，且已经在文献[35，36]中进行了多次网格收敛性验证，并且对NLF(2)-0415无限展长后掠翼、镰刀形后掠翼和椭球大迎角工况等经典算例进行了计算。结果均表明本文所构建的模式在不可压缩边界层广泛的算例验证中均取得了较好的预测结果。下面将对两个跨声速大后掠翼流动进行验证和分析。

2.1 DLR-F4翼身组合体

DLR-F4翼身组合体在欧洲跨声速风洞（ETW）中通过温度敏感涂层（TSP）技术进行了转捩测量试验，该构型通常被用于检验跨声速后掠翼表面的T-S波转捩、激波诱导附面层分离致转捩和横流转捩[39]。机翼前缘后掠角27.1°，试验数据和稳定性分析结果表明，横流主导了内侧机翼的转捩，而T-S波失稳或激波诱导附面层分离出现在中部和外侧机翼表面。该试验来流马赫数为0.785，基于平均气动弦长的雷诺数为6.0×106，自由来流湍流度小于0.05%，因此可将其视为低扰动环境。宋文萍等[10]在DLR-F4机翼上进行了标准的LST分析，证实了横流失稳主导机翼内侧区域的转捩现象。此外，与测量所得的转捩位置相比，文献[10]指出NTS和NCF的临界值可以分别设置为10.5和7.5。图1对比了不同网格尺度下的转捩预测结果。由图可知，随着网格的加密，转捩预测位置逐渐趋于收敛。最终选择Fine网格进行所有工况的计算，描述边界层的O网格内部壁面法向网格单元的数量为401，近壁第一层网格尺度为1×10-6m，与壁面相邻单元的y+（1）的平均值等于0.95。横流驻波扰动增长因子输运模式能够很好地预测出机翼内侧的横流转捩。与Coder等发展的NTS模式相结合组成的NTS-NCF模式可以很好地捕捉到横流不稳定性、T-S波转捩和激波诱导附面层分离致转捩。

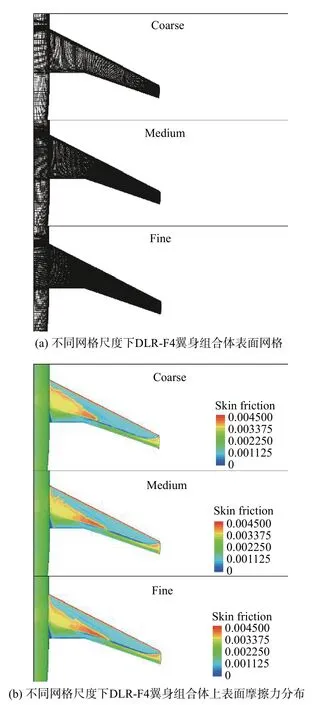
图1 不同网格尺度下DLR-F4翼身组合体上表面转捩预测结果Fig.1 Transition prediction results for the upper surface of DLR-F4 wing-body configuration resolved with different grid scales

图2 DLR-F4翼身组合体上表面转捩预测结果与风洞试验结果的对比Fig.2 Comparison of the transition results for the upper surface of DLR-F4 wing-body configuration between the prediction and the experiment

图2 展示了在迎角α = -0.87°（CL= 0.5）、α = -1.58°（CL=0.4）和α=-2.59°（CL=0.3）时，DLR-F4机翼上表面的摩擦阻力系数云图与试验测得的TSP结果。可以清晰地发现，与风洞试验结果相比，本文发展的

进一步截取α=-0.87°（CL=0.5）工况的上表面的NTS和NCF云图，如图3所示。由图可知，在内翼段（y =0.1 m）处，横流驻波主导失稳。向翼梢移动，在kink位 置（y =0.24 m）和 接 近 翼 梢 的 位 置（y =0.5 m），则分别是T-S波和激波诱导附面层分离主导失稳。产生这种不同转捩机制的原因主要是内翼段上表面为顺压梯度，kink处有双层逆压梯度，外翼段则为强逆压梯度，直接导致附面层分离，进而触发转捩。这些结论与参考文献[10]的标准LST分析结果一致。

2.2 ARA翼身组合体

层流模型（LFM）翼身组合体是由英国飞机研究协会（ARA）和西北工业大学（NPU）联合设计的。它是一架无尾飞机，用于研究跨声速大后掠机翼（35°）表面的自然层流（NLF）和混合层流控制（HLFC）[40-41]。该翼身组合体于2017年4月在ARA风洞中进行了试验。风洞中的机身和机翼几何尺寸如图4（a）所示；进行CFD数值模拟的Fine网格分布与DLR-F4构型类似，如图4（b）所示。

来流马赫数为0.7，参考弦长为0.562 m，参考面积为0.857 7 m2，来流湍流度0.2%，单位米雷诺数为1.2357×107m-1，风 洞 试 验 迎 角 为-0.99°、-2.16°和-3.34°。传统的LST分析结果表明NCF,crit值为7.0[40-41]。

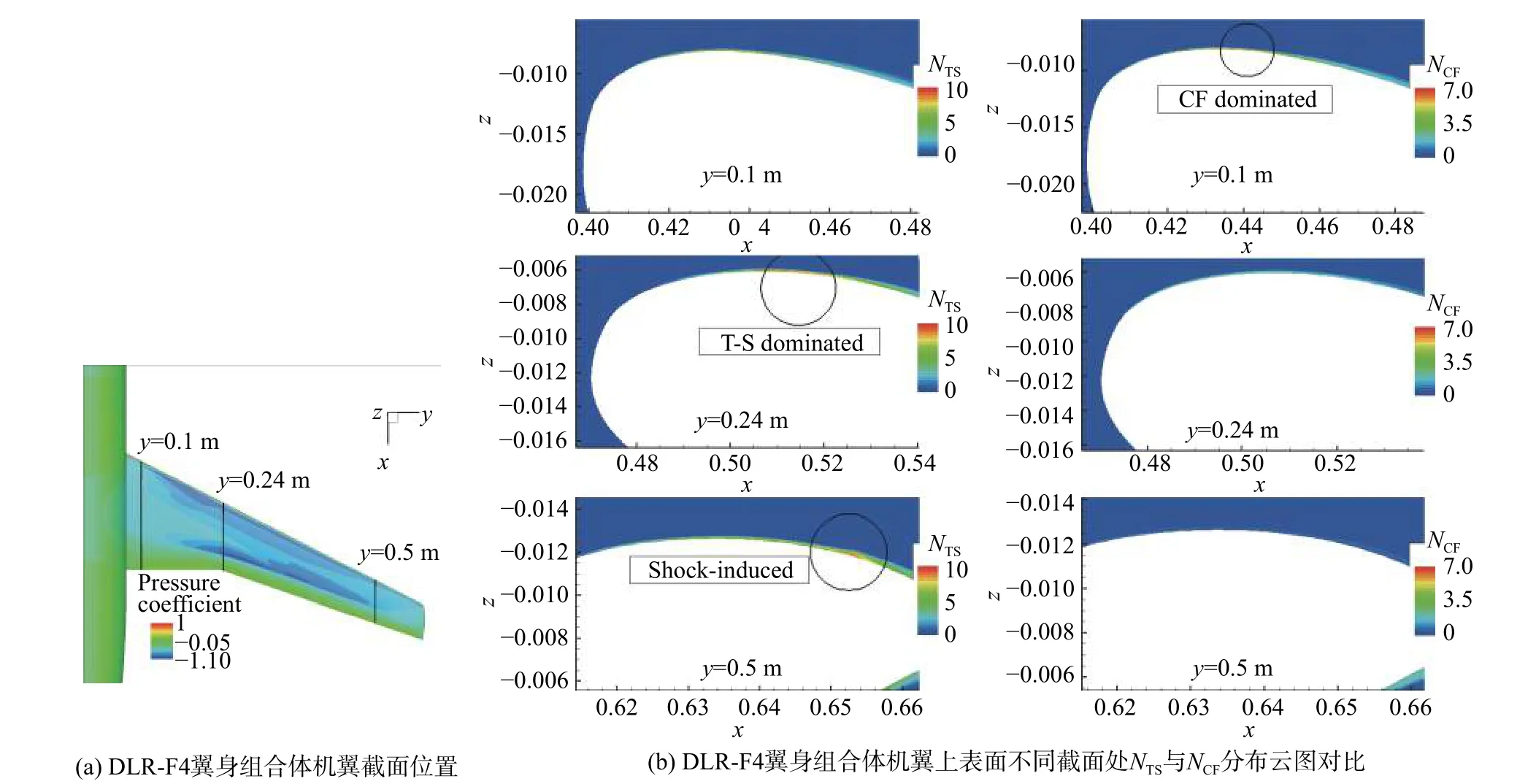
图3 DLR-F4翼身组合体上表面N TS与N CF分布云图对比Fig.3 Comparison of the contours for N TS and N CF on theupper surface of DLR-F4 wing-body configuration

图4 ARA翼身组合体的风洞试验构型尺寸和CFD网格图Fig.4 Wind tunnel model and CFDgrid of ARA wing-body configuration

经过本文NCF模式的计算，在不同迎角下，机翼展向y = 1.05 m位置的压力分布与试验结果吻合良好，如图5所示。图6对比了本文NCF模式预测所得的横流驻波NCF因子与传统标准LST分析结果，验证了本文模式总是能够捕捉到最不稳定的最大N值。图7则展示了在-3.34°迎角下，Coder的NTS模式与本文NCF模式的预测结果对比，可见Coder的NTS模式对于横流转捩的预测是失效的，本文NCF模式则能够较为准确地对横流转捩现象进行预测。

图5本文模式预测所得不同迎角下机翼表面（y = 1.05 m）压力系数分布与ARA风洞试验结果的对比Fig.5 Pressure coefficient distributionson the upper surface of the wing (y = 1.05 m)compared between themodel prediction and the wind tunnel experiment for different anglesof attack

图8 展示了不同迎角下NCF模式预测结果与风洞试验结果的对比，两者吻合良好。风洞试验显示机翼上表面出现的锯齿状转捩区也验证了横流驻波主导失稳这一事实。由图5可知，不同迎角下机翼上表面的顺压梯度强弱不同，迎角-3.34°下的顺压梯度最强，因而横流涡的发展更为迅速，转捩位置最靠前。DLR-F4机翼前缘后掠角为27.1°，ARA机翼前缘后掠角为35°，镰刀翼前缘后掠角从0°变化到55°，椭球表面的当地后掠角范围更大，变化更为剧烈。当地后掠角和顺压梯度这两个对横流转捩非常敏感的影响因素均被本文NCF模式精准捕捉得到，验证了其合理性和准确性。

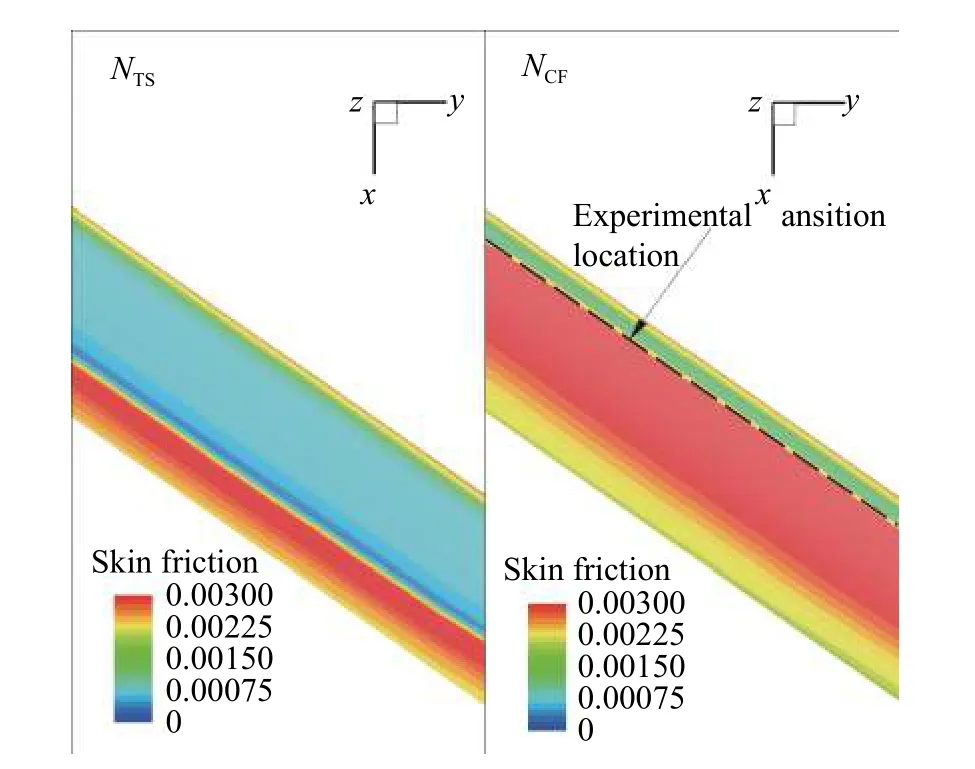
图7 Coder的N TS模式与本文N CF模式预测结果对比（α = -3.34°）Fig.7 Comparison of the prediction results between Coder’s N TS model and the present N CF model (α = -3.34°)

图8 不同迎角工况下本文N CF模式预测所得机翼上表面摩擦力系数云图与风洞试验结果对比Fig.8 Comparison of the skin-friction coefficient contours on the upper surface of the wing between the present N CF model prediction and the wind tunnel experiment for different anglesof attack

3 结论

基于MIT的Drela团队简化线性稳定性理论的思想，Coder等基于当地化变量首次构造了流向Tollmien-Schlichting（T-S）波的扰动增长因子输运模式。本文作者在2019年[35]首次提出了横流驻波的扰动增长因子输运模式，并对其进行了可压缩修正[36]，使其可以适应亚声速和跨声速复杂气动外形的边界层流动。主要创新点有以下几个方面：

1）揭示了横流驻波的最大包络N值与基本流中边界层特征厚度、横流形状因子、横流最大速度分量、横流雷诺数、壁面温度、边界层边缘马赫数的函数映射关系，并对方程源项的构造进行了可压缩修正和改进；

2）使用横流强度因子实现了对横流最大速度分量的当地化求解，并对计算公式进行了改进；

3）使用螺旋度雷诺数实现了对横流雷诺数的当地化求解，并对计算公式进行了改进；最终形成了基于当地变量的适用于亚跨声速边界层的横流驻波扰动增长因子输运模式。

本文选取了纯粹针对跨声速边界层横流转捩的风洞试验标模。不同迎角导致顺压梯度强度不同，进而使得横流强度不同，这些都能被当前模式精确捕捉，充分验证了其在跨声速工况下的合理性和准确性。未来将继续致力于让流动稳定性分析变成一个CFD问题，能够真正将传统的稳定性理论推广到工程复杂外形绕流的转捩预测。基于线性稳定性理论对超声速边界层的Oblique T-S波、横流波和Mack模态扰动的增长因子进行模式化构造并且探索较为普适的临界N值判据将是下一步的研究方向。

致谢：感谢史亚云博士和杨体浩博士提供ARA风洞试验构型和数据。