火箭整流罩脉动压力环境数值模拟与优化设计
2023-01-05樊宇翔
樊宇翔,于 洋,席 柯,赵 瑞,*,任 方
(1.北京理工大学宇航学院,北京 100081;2.北京强度环境研究所可靠性与环境工程技术重点实验室,北京 100076;3.中国兵器工业导航与控制技术研究所,北京 100089)
0 引言
飞行器在主动飞行阶段,整流罩外脉动压力会对壁面产生随时间变化的激励力,这是飞行器结构设计中需要考虑的关键问题之一。大量的实验研究表明,气动噪声是一种强噪声,声压总级高达130~170 dB,低中高频都有所覆盖,其不但会破坏飞行器结构,还可能以声透射方式进入飞行器内部,影响内部仪器正常工作并对人员造成伤害,甚至引发严重的飞行事故[1-3]。因此,整流罩作为保护飞行器的重要结构,对改善其气动噪声环境具有重要意义。整流罩最恶劣的噪声环境主要有两个阶段:第一阶段是发射阶段的喷流噪声;第二阶段则是在飞行器主动飞行时,整流罩表面由于非连续过渡的存在,流动容易出现膨胀、分离、压缩等结构,这些流动结构的相互影响,尤其是在跨声速阶段,会使得整流罩受到极大的脉动压力,形成极为恶劣的噪声环境[4-6]。
目前,对飞行器脉动压力环境预测的方法主要有数值模拟法、经验/半经验工程算法和风洞试验法。对于数值模拟法,Tsutsumi等[7]采用改进的延迟脱体涡模拟方法(improved delayed detached-eddy simulation,IDDES)[8]获取了典型整流罩结构的脉动压力等特征参数。赵瑞等[9]基于五阶加权本质无振荡(weighted essentially non-oscillatory,WENO)格式构造隐式大涡模拟方法(implicit large eddy simulation,ILES),对跨声速来流条件下火箭整流罩外头锥部位噪声环境进行了数值模拟计算,验证了该计算方法的可行性,并通过瞬时流场分析,改进了脉动压力经验预测公式[10]。此外,他们还对比了整流罩头锥不同母线形状对脉动压力环境的影响效果,指出冯·卡门母线形状有利于减缓头锥脉动压力环境[11]。石小潘等[12]采用脱体涡方法(detached eddy simulation,DES)预示了火星进入器在跨声速阶段时的脉动压力环境。之后他们又采用动网格技术,耦合了刚体运动方程,对火星进入器强迫震荡运动开展了非定常数值模拟,指出强迫振荡会诱导大底脱体激波进行同频率振动,进而导致进入器大底的脉动压力环境极为恶劣[13]。
综上所述,目前研究飞行器壁面脉动压力环境的数值模拟方法主要依靠DES和LES。但以上两种方法主要针对分离流动,而实际飞行器绕流往往以附体流动为主导,DES和LES需要在边界层内布置较密的网格才能捕捉小尺度湍流脉动结构,这样会耗费大量的计算资源[14]。为解决上述问题,Morris等[15]提出使用RANS模型先求解流场,再求解非线性扰动方程以获得声场,该方法准确地计算了三维射流声场问题。Batten等[14]将上述方法进行了改进,提出一种非线性噪声求解器(non-linear acoustic solver, NLAS)方法。这种方法采用非线性湍流模型(nonlinear reynolds averaged Navier-Stokes simulation, Nonlinear RANS)进行流场求解,求解效率较高;而无法求解的小尺度量则进行湍流重构[16-17],兼顾了亚格子尺度声源的影响。因此相比于LES与DES方法,NLAS在保证低耗散的同时降低了网格量。近年来,NLAS方法被成功应用于空腔噪声模拟[18-20]、高铁噪声模拟[21]、飞机机翼噪声模拟[22-23]、射流噪声模拟[24]等。
虽然目前关于NLAS方法的应用已经取得了一些进展,但将其应用于整流罩脉动压力环境的研究还较少。任淑杰等[25]使用RANS/NLAS方法研究了跨声速阶段火箭表面典型位置处的脉动压力,给出了不同马赫数下的声压级与均方根脉动压力系数,但是并未给出直观的流动现象,也没有分析迎角的影响。因此,本文使用RANS/NLAS方法,继续深入研究整流罩的壁面脉动压力环境产生机理并进行优化设计。文章首先对典型的整流罩头锥外形进行方法验证;然后研究头锥-柱-倒锥外形整流罩的脉动压力环境,分析迎角对脉动压力的影响规律;最后采用优化倒锥型线的方式抑制脉动压力环境。
1 控制方程
1.1 湍流模型
为准确描述NLAS方程中的非线性项,需采用一种非线性的湍流模型获取雷诺应力分布。本文用两方程cubick-ε湍流模型[26-29],同时引入Favre平均[30-33]。即在雷诺N-S(RANS)方程组的基础上提出密度加权平均概念,对压强和密度采用时间平均,其他变量采用密度加权平均,存在以下Favre分解:f=。Favre平均解决了RANS方程组处理可压缩流动较为复杂的问题,通适于不可压缩流动与可压缩流动,其输运方程如下:
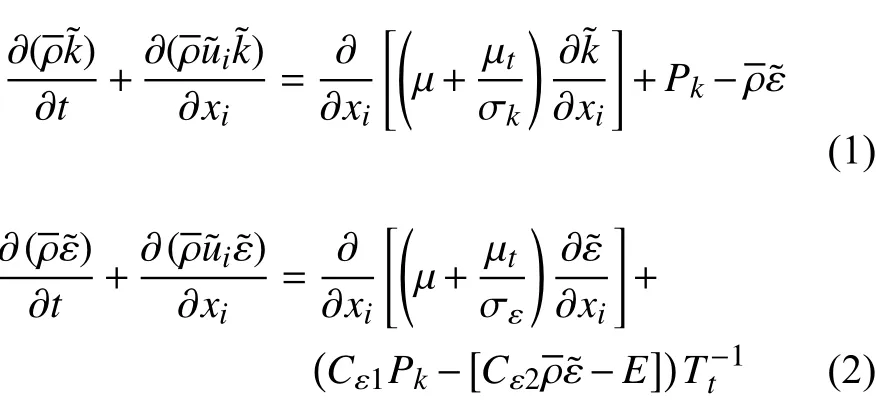
式中:常量Cε1= 1.44,Cε2= 1.92,σε= 1.3,σk= 1.0,
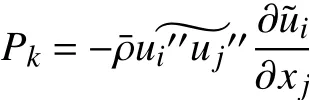
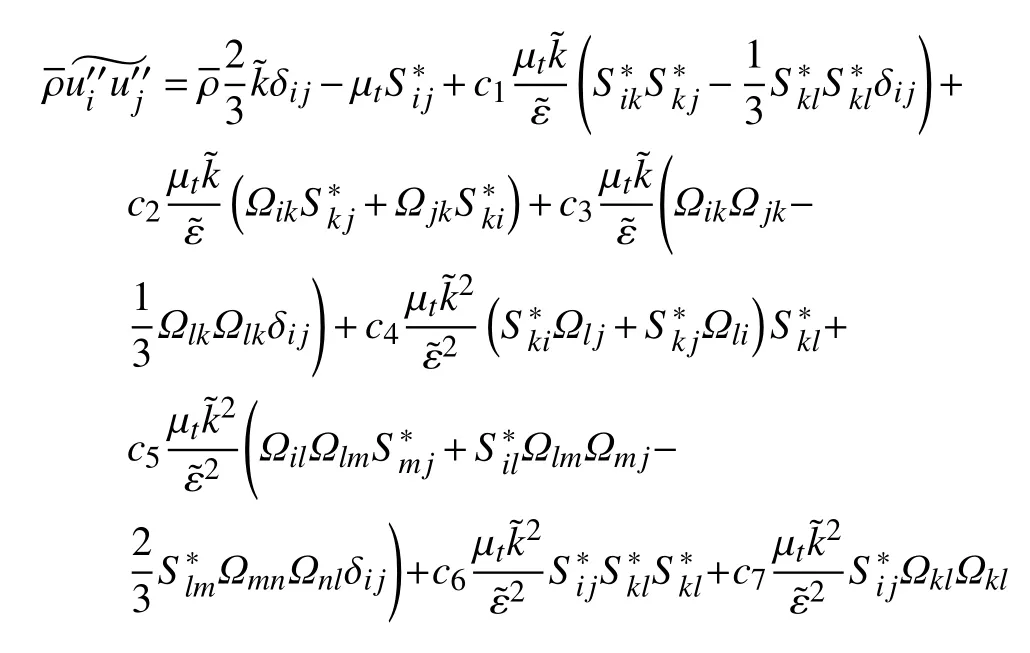
系数分别为:

其中:Pk为湍动能生成项,ρ为密度,t为时间,ui为i方向上的速度分量,μ为黏性系数,μt为涡黏性系数,Tt为时间尺度,常量AEτ= 0.15,Aμ= 0.01,Cτ=
1.2 NLAS控制方程
NLAS将湍流模型获取的雷诺应力和重构的小尺度亚格子源项共同作为声学扰动方程的源项,通过求解声学扰动方程,模拟脉动压力环境。

将流体变量分为统计平均项和扰动项:将其代入Navier-Stokes方程组并进行重新整理,等式左边为扰动项,右边为平均项,可得非线性的扰动方程:
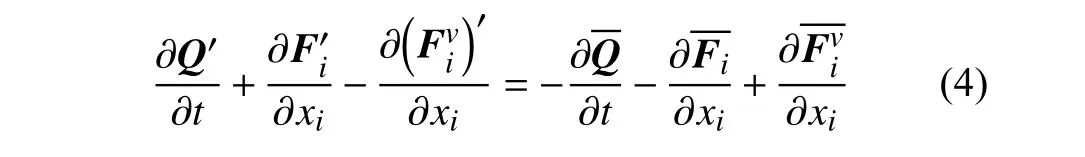
式中:

其中:p为压力;θi为传热项;δij为克罗内克符号;τ为剪切应力;e为单位体积能,表达式为:
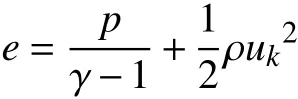
忽略式(4)中的密度扰动并进行时间平均处理,得:
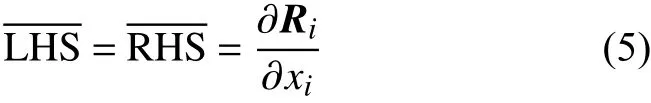
式中:LHS与RHS分别代表式(4)的左项与右项,Ri是标准雷诺应力张量和湍流热通量相关项,由左式扰动项化解而来,表达式为:
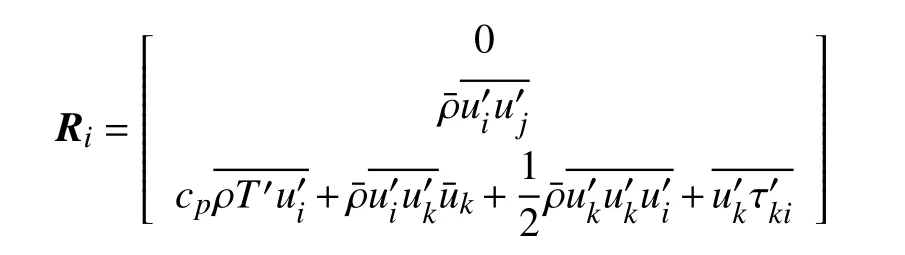
式中cp为定压比热容。Ri中各项由之前的cubick-ε求解得出。
对于无法求解的小尺度脉动量,需要使用湍流统计结果重构作为亚格子源项。湍流重构指的是在cubick-ε求解得到的平均流场基础上产生对应的扰动速度场[23],再叠加到非线性扰动方程求解过程中。在LES和声学相关领域,湍流重构可以显著降低计算成本[17]。Kraichnan[16]在1970年就提出了一种详细的湍流重构方法,用傅里叶模式叠加描述时间与空间关系,不过该方法只适用于各向同性湍流。之后Smirnov等[17]提出了基于雷诺应力张量相似变换的张量尺度概念,对Kraichnan的方法进行了改进,将其成功应用到了各向异性湍流。最后Batten等[14]对张量尺度进行了简化处理,避免了计算相似变换的过程,其湍流扰动速度的傅里叶模式方程如下:
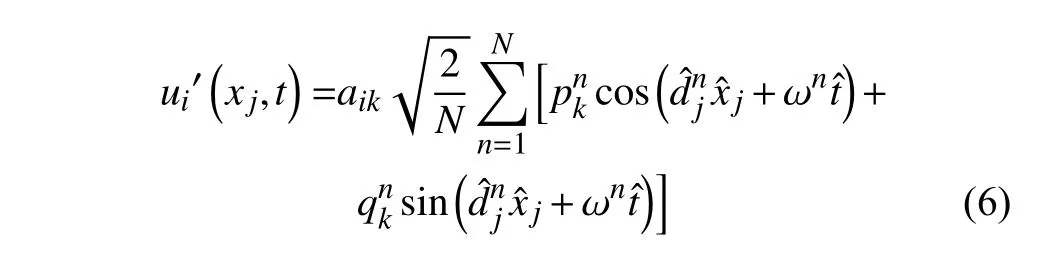
式中:
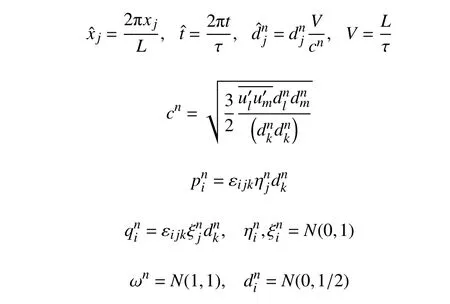
其中:为网格中特定位置的速度扰动;xj为笛卡尔坐标系中的位置;aik为当地雷诺应力张量的Cholesky分解;L为湍流长度尺度;τ为湍流时间尺度;与为余弦和正弦函数的系数;cn为速度缩放尺度;向量积运算的置换张量; 是高斯正态分布函数,其平均值为,标准偏差为β。上述湍流重构过程都是以cubick-ε计算的相关张量和湍流长度尺度与时间尺度作为输入,重构的结果将在式(4)时间迭代过程中作为扰动项加入。
此外,NLAS可以使用原来的RANS计算网格来模拟压力脉动的传播,也可以通过插值在新的计算网格上进行求解。相对于RANS,NLAS对网格的要求较低,可大量降低网格量,节省计算成本,更好地适用于工程复杂外形。空间离散采用耦合TVD限制器的二阶迎风格式,其限制器为Min-mod,声场计算的时间积分采用双时间步长隐式方法。迭代时,采用多重网格法加速收敛的同时,使用MPI并行计算,减小计算时间,提高计算效率。
2 NLAS方法验证
2.1 验证模型
采用文献[7,9]研究的整流罩外形作为验证算例,模型如图1、图2所示。计算迎角为0°,马赫数为0.8,基于圆柱段直径的雷诺数为2.66×106,计算网格参照文献[9],采用1/4模型,第一层网格高度y+<1。文献[7]采用1/72模型,网格量为1100万。在RANS计算中,远场边界为特征边界条件,对于NLAS声学计算,远场为吸收层边界,以消除远场边界反射,时间步长2×10-7s。为避免初始计算数值扰动,舍弃掉初始3000步数据。
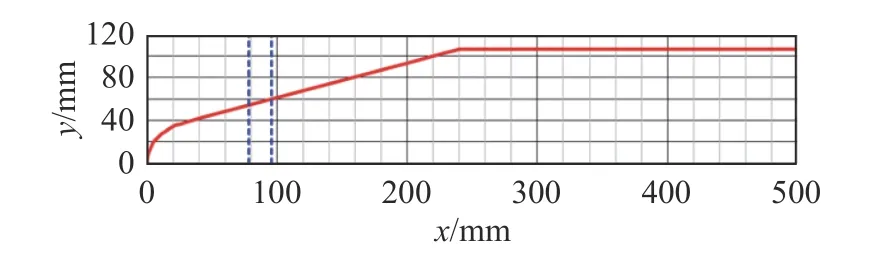
图1 整流罩模型的几何尺寸[7]Fig.1 Rocket fairing model geometry[7]

图2 风洞试验模型[7]Fig.2 Wind tunnel model of the rocket fairing[7]
2.2 计算结果对比

图3 壁面压力系数(时均)轴向分布对比Fig.3 Comparison of time-averaged surface pressure coefficient Cp profilesalong the axis-direction
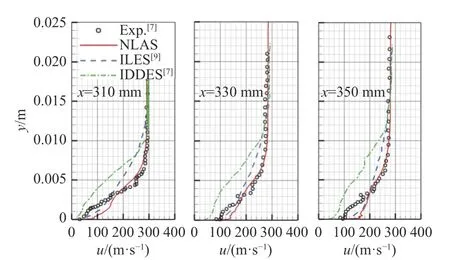
图4 再附点附近的流向速度型(时均)分布对比Fig.4 Comparison of time-averaged streamwise velocity profiles around the reattachment point
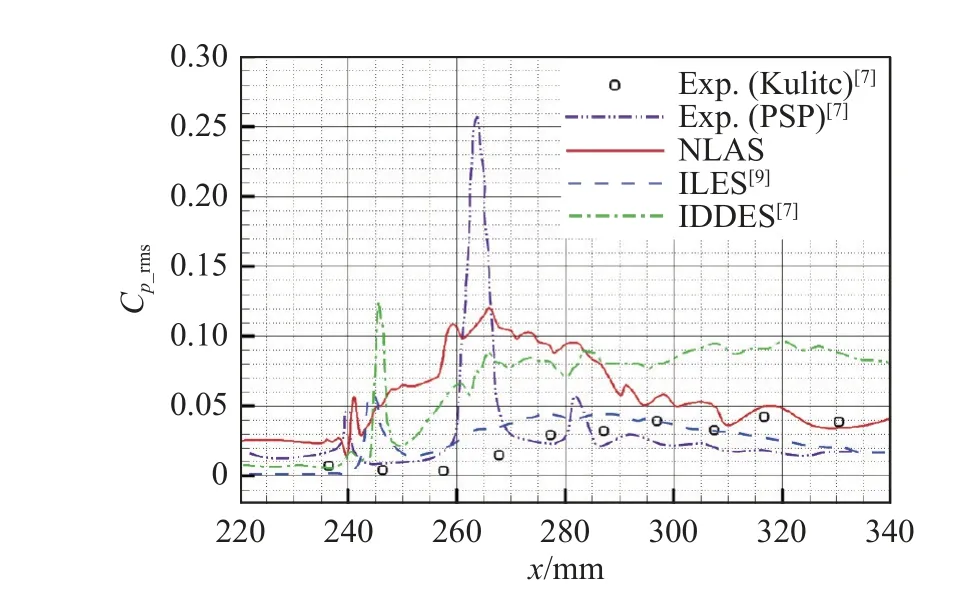
图5均方根脉动压力系数分布对比Fig.5 Comparison of root-mean-square fluctuating pressure coefficient Cp_rms profilesalong the axis-direction
图3 ~图5为RANS/NLAS声场计算结果与文献结果的对比。其中,文献[7]和文献[9]分别使用IDDES方法和基于五阶WENO格式的ILES方法开展了数值计算。图3为时均后壁面压力系数轴向分布图,通过与试验值和文献计算结果进行对比发现,使用NLAS方法能以较少的网格量获得更优的结果,与试验值也更为接近。图4为时均后再附点附近流向速度型分布对比图,从图中同样可以看到,本文使用的NLAS方法能够更加准确地预测出速度分布。图5为整流罩壁面均方根脉动压力系数分布对比图。均方根脉动压力系数Cp_rms的计算公式为:Cp_rms=是表征噪声环境的重要参数;其中,是均方根脉动压力,代表壁面上某点脉动压力的总强度,q∞=0.5ρ∞是来流动压头。可以看到,均方根脉动压力系数在折角区内显著增加,过折角之后开始下降,附体之后与实验值更吻合。头锥折角区域为激波/边界层干扰的主要区域,图中试验值的差异是由于Kulite传感器布局的限制,使其并没有捕捉到折角区域的峰值[7]。不同数值模拟方法都有预测到这一段区域的峰值,峰值的具体大小与位置的差异应该与网格量有关[7]。相比于文献[9]的基于五阶WENO格式构造的ILES方法,以及文献[7]的使用1100万网格量(1/72模型)的IDDES方法,本文采用更少的网格量以低阶计算格式进行计算,计算效率更高,计算精度较好。
3 整流罩外流场数值模拟分析与型线优化设计
3.1 几何模型和计算网格
计算模型为头锥-柱-倒锥的整流罩风洞模型,模型已做特定缩放处理,图6为外形示意图。
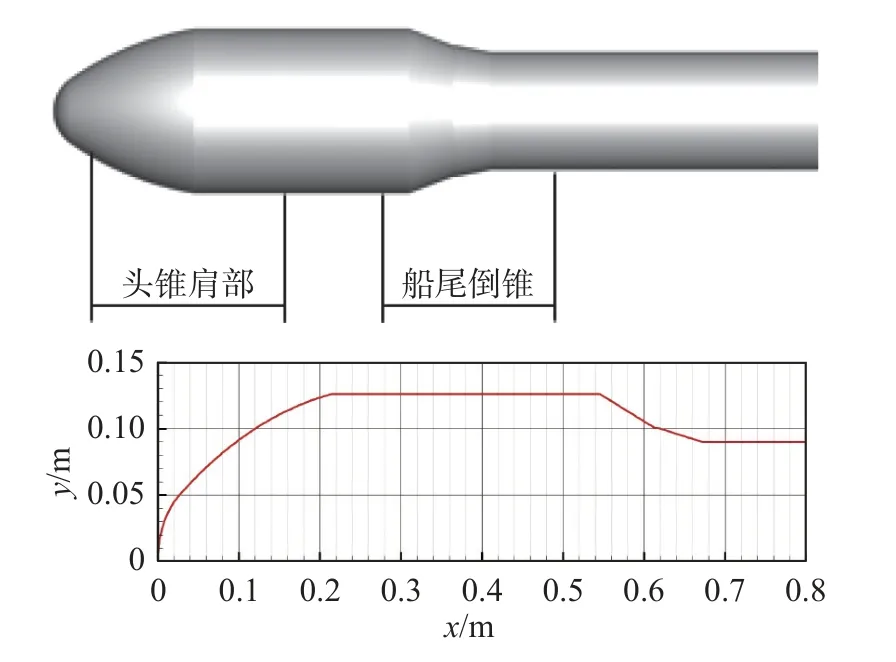
图6 整流罩外形Fig.6 Rocket fairing shape
计算模型为1/2模型,图7为RANS计算与NLAS计算的网格对比,RANS计算网格量约为620万,第一层网格高度y+<1,NLAS计算网格量约为370万。边界条件与算例验证相同,自由来流马赫数为0.8,单位雷诺数为1.58×107/m,迎角为0°、4°、8°,时间步长为 5×10-6s,共计算18000步,舍弃初始3000步数据。

图7 RANS与NLAS网格比较Fig.7 Comparison of meshes used by RANSand NLAS
3.2 计算结果分析
3.2.1 定常RANS流场分析
图8为迎角8°下的整流罩流场,对称面为马赫数云图,壁面为无量纲压力云图。亚声速来流沿整流罩头部加速,使得壁面压力不断降低,在头锥和圆柱段交界处即肩部附近显著降低达到最小值,过折角后膨胀加速形成一道斜激波,过激波后速度降低为亚声速,壁面压力增大。在肩部区域因为激波强逆压梯度发生分离,形成分离区,产生正激波,两道激波构成“λ”型,如图9的肩部放大图所示,对称面改用无量纲密度云图着色。而在倒锥处,由于外形突然的收缩产生大分离区,如图10所示。此外由于有迎角的存在,在肩部附近,背风面的气流迅速加速,流速更快,形成更大的高速区域;在倒锥处,迎风面的分离区更大,再附点靠后,背风面的分离区减小。
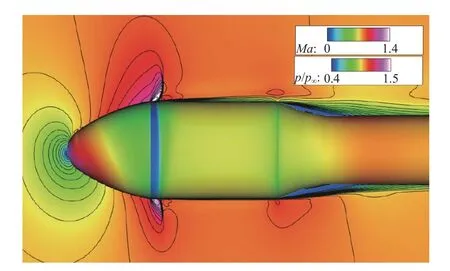
图8 壁面压力与对称面马赫数云图Fig.8 Contours for the pressure on the wall and the Mach number in the symmetry plane
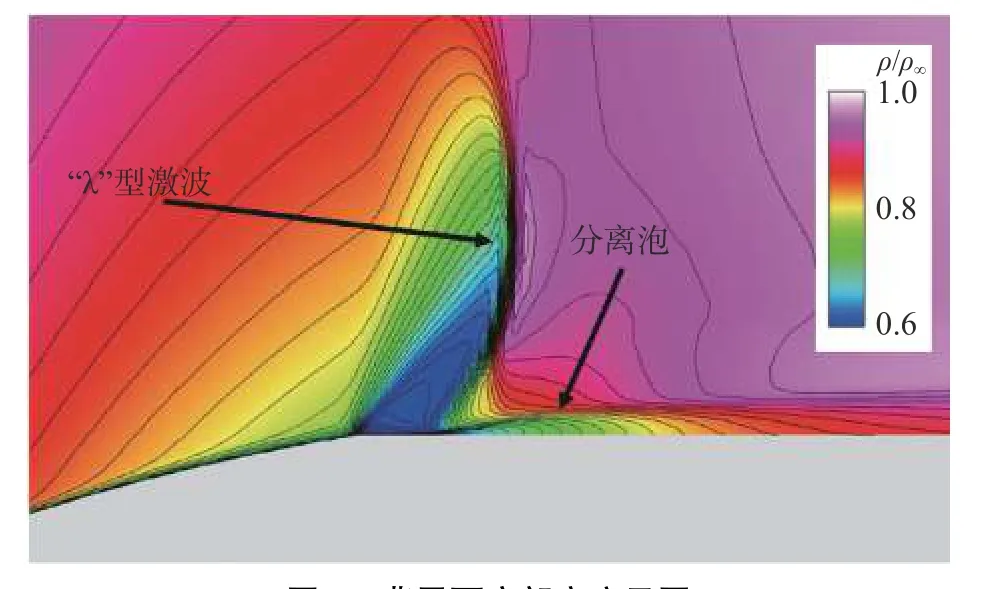
图9 背风面肩部密度云图Fig.9 Density contour in theleeward side of the cone-cylinder

图10 背风面倒锥部位分离区Fig.10 Separation zone in the leeward side of the inverted cone
3.2.2 NLAS脉动压力计算分析
迎角的存在导致流动在背风面肩部产生了更强的逆压梯度,附体边界层发生明显分离,脉动压力环境恶劣,因此本次研究主要针对背风面。
图11为NLAS计算所得的整流罩肩部瞬时数值纹影图,可以观察到其上游的斜激波主要在圆柱段与头锥连接的拐角处附近;分离剪切层不稳定、极易破碎,并向上游传播,其与激波相互作用,使得分离区的范围和激波位置前后震荡;在激波/边界层的干扰下,形成了极其恶劣的脉动压力环境。

图11肩部瞬时数值纹影图Fig.11 Instantaneous numerical schlieren images of the cone-cylinder
图12 为整流罩背风面均方根脉动压力系数沿轴向分布的风洞试验与数值计算结果对比图,各状态下计算结果和试验数据均已经过特定参考值无量纲化处理(下文同)。肩部处由于激波/边界层的干扰,产生了较大的峰值。倒锥处,分离区的不断扰动使得脉动压力增大,导致了倒锥部峰值的出现。NLAS预测结果与试验值较为吻合。
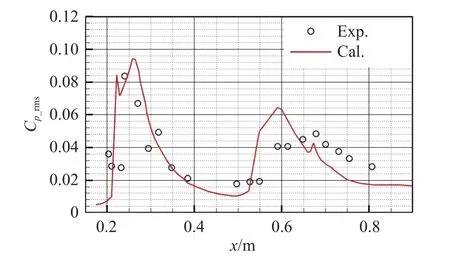
图12背风面均方根脉动压力系数分布(Ma = 0.8,α = 8°)Fig.12 Root-mean-square fluctuating pressure coefficient Cp_rms distributionsin the leeward side(Ma = 0.8,α = 8°)
图13 为不同迎角下背风面肩部附近的均方根脉动压力系数分布图。脉动压力系数随迎角的变化比较复杂,整体有随迎角增大而增大的趋势,这主要是因为随着迎角的增大,肩部激波/边界层的影响范围增大,导致了更加恶劣的脉动压力环境。
图14为不同迎角下背风面倒锥的均方根脉动压力系数分布图,可以看出在倒锥部位,随着迎角的增大,均方根脉动压力系数会减小,这主要是因为背风面倒锥部位的分离区会因迎角的增大而减小,如图15所示,分离区产生的扰动作用减弱,从而使得均方根脉动压力系数值降低。
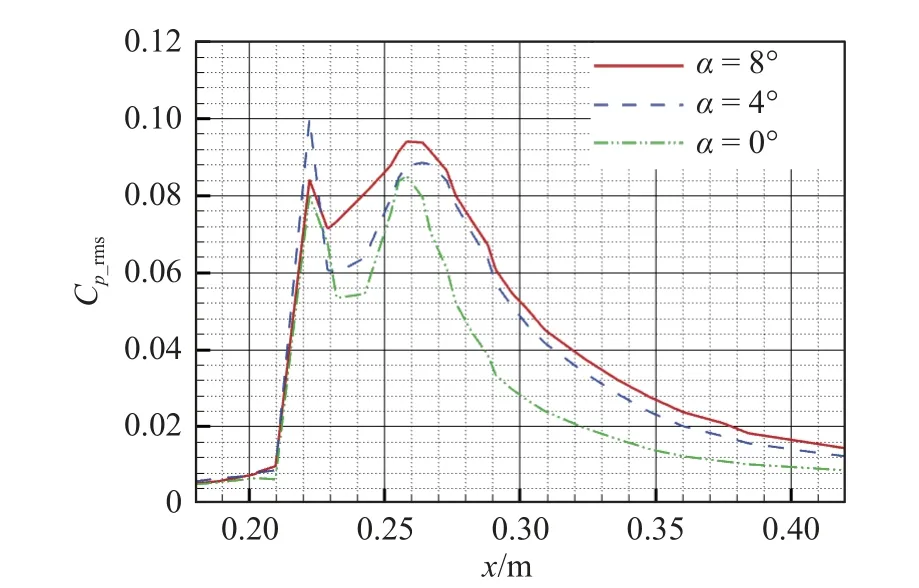
图13 不同迎角下肩部均方根脉动压力系数分布(Ma = 0.8)Fig.13 Root-mean-square fluctuating pressure coefficient Cp_rms distributions on the cone-cylinder at different angles of attack(Ma = 0.8)
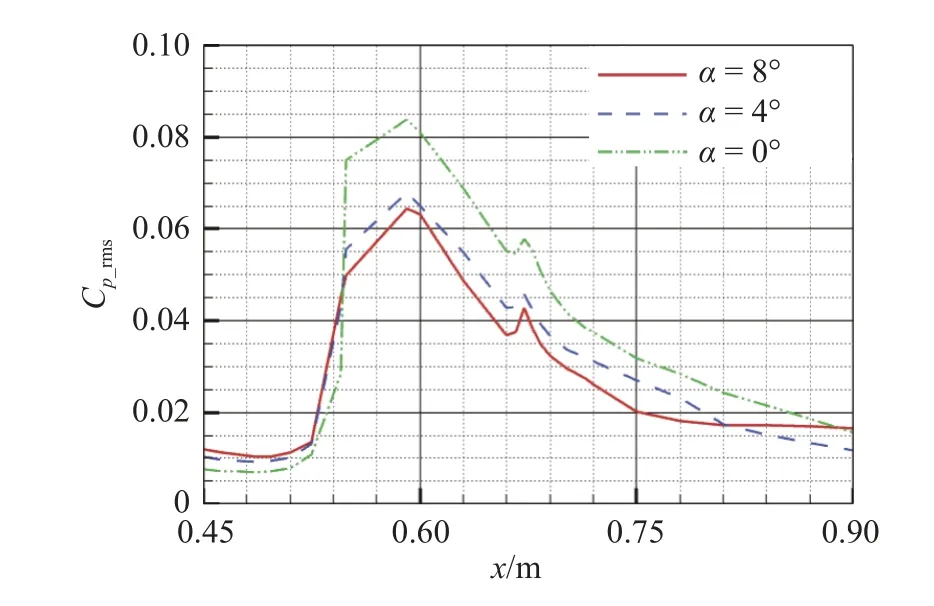
图14 不同迎角下倒锥处均方根脉动压力系数(Ma = 0.8)Fig.14 Root-mean-squarepressure coefficient Cp_rms distributionson the inverted cone at different anglesof attack(Ma = 0.8)
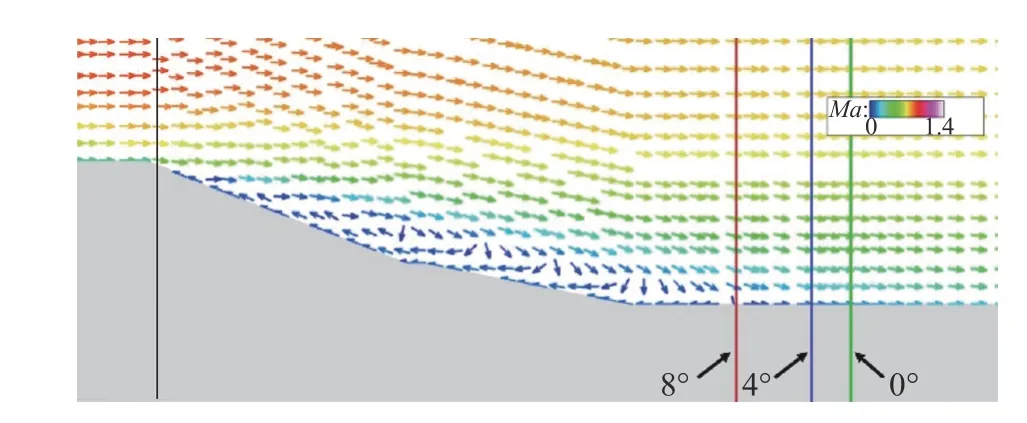
图15 不同迎角下倒锥处分离区大小Fig. 15 Separation zone on the inverted cone at different angles of attack
3.3 倒锥型线优化设计
如图16所示,为抑制整流罩倒锥部位的脉动压力,改善其噪声环境,现设计三种不同的方案进行优化。方案一:采用一段直线连接两端;方案二:采用分别与两端相切的正弦曲线连接两端;方案三:采用“切线弧+圆弧”将两端连接,尾端的圆弧半径为1.8×10-2m。来流工况见3.1节,迎角为8°。
图17为不同外形背风面时均摩擦力系数Cf轴向分布图,其计算公式为:Cf=其中τwall是壁面剪切应力。通过对比可以看出,“切线弧+圆弧”外形的摩擦力系数下降缓慢,到达零值后小幅下降,然后再迅速回升到零值,流动缓慢减速分离,分离点靠后,分离效果较弱,分离区最小;“正弦”外形相较于“切线弧+圆弧”外形效果较差;原始外形和“直线”外形因在起始端的非光滑过渡,导致摩擦力系数迅速下降,而原始外形由于中间段外形的改变,使得摩擦力系数有所回升,两种外形的分离区都较大,分离效果较强。各方案的分离区情况如图18所示。

图16 倒锥部位轮廓线Fig.16 Outline profiles of the inverted cone
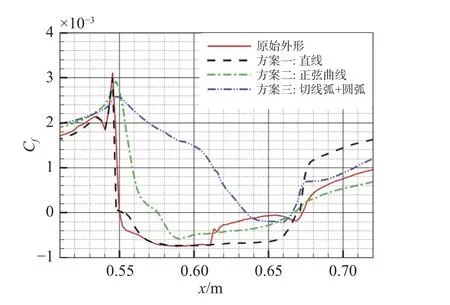
图17 不同外形背风面倒锥处时均摩擦力系数分布Fig.17 Time-averaged friction coefficients Cf distributions in the leeward side of different inverted cones
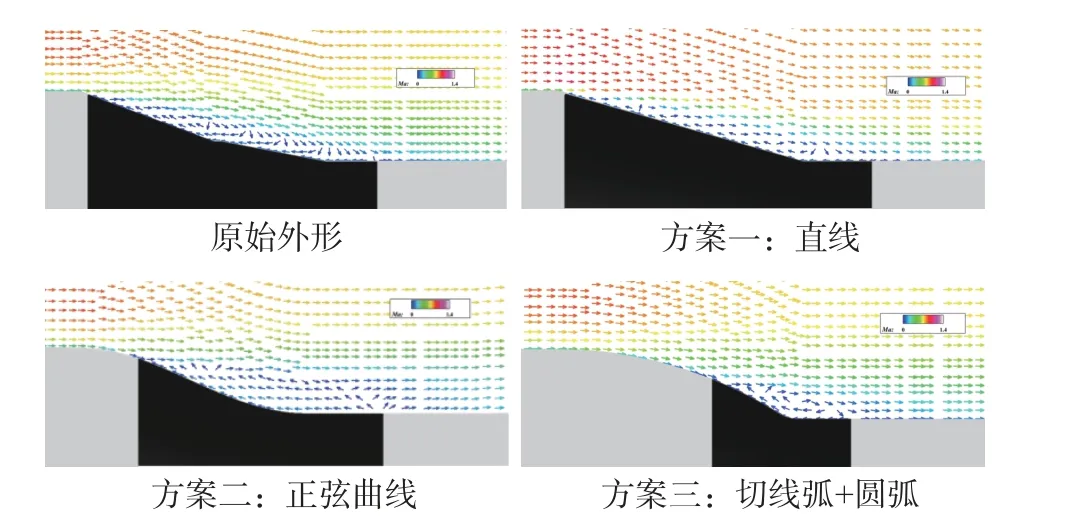
图18 不同倒锥部位分离区Fig.18 Separation zonesof different inverted cones
图19为不同外形背风面均方根脉动压力系数轴向分布对比图。对于“直线”外形与原始外形,在起始端,强烈的流动分离导致该区域压力脉动剧烈,均方根脉动压力系数增大;“直线”外形在肩部之后为直线过渡,脉动压力减弱,而原始外形由于中间依旧存在折角的非光滑过渡,数值波动上升,达到峰值;在尾端,由于非光滑过渡和分离再附的影响两者均再次出现峰值。对于“正弦”外形与“切线弧+圆弧”外形,在起始端,均方根脉动压力系数增长相对缓慢且幅值较小;但在中间段,“正弦”外形斜率较大,会引起较强的脉动压力,达到峰值,而“切线弧+圆弧”外形的连接更为平缓,数值更低;在尾端,“正弦”外形的相切连接减弱了分离再附的剧烈脉动,均方根脉动压力系数快速下降,而“切线弧+圆弧”外形在尾端出现峰值。尾端由于分离再附的脉动影响较为剧烈,数值都相对较高。综合来看,“切线弧+圆弧”外形方案的优化效果更好。
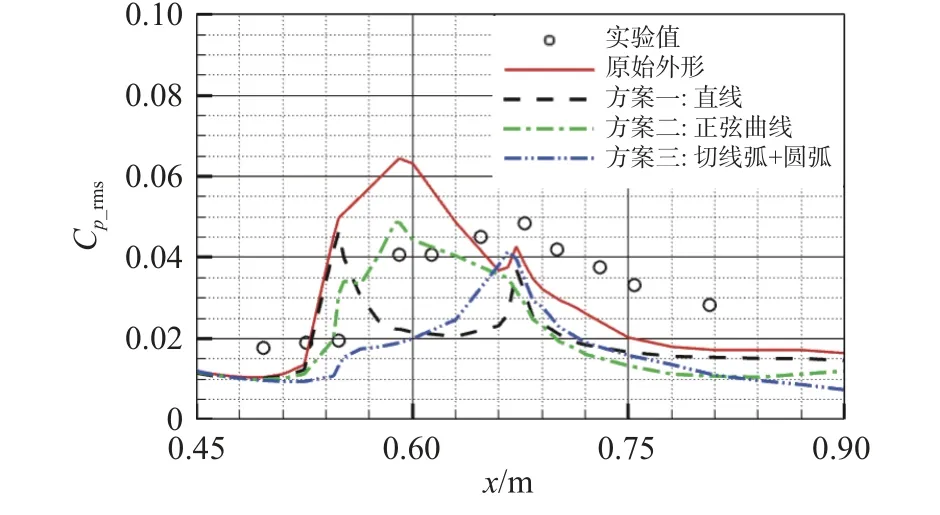
图19 不同外形背风面均方根脉动压力系数分布Fig.19 Root-mean-squarepressure coefficient Cp_rms distributions in the leeward side of different inverted cones
4 结论
本文使用RANS/NLAS的非线性噪声求解方法对跨声速条件下火箭整流罩外部脉动压力环境进行了数值模拟计算,研究了迎角对脉动压力的影响,并采用优化倒锥型线的方式对倒锥部位的脉动压力环境进行了改善。通过算例验证,与试验结果和文献结果对比分析,得出以下结论:
1)RANS/NLAS可以准确预测跨声速条件下整流罩外的非定常流动现象;并且由于NLAS方法对网格要求较低,可减少声场计算的网格数量,降低计算成本,所以其适合于工程复杂外形脉动压力环境计算。
2)在跨声速来流条件下,气流经过火箭整流罩的头锥肩部后会形成“λ”型激波和分离泡;在倒锥部位会产生大范围的分离区,导致两区域的脉动压力环境极为恶劣,均方根脉动压力系数达到峰值。
3)随着迎角的增大,背风面肩部激波/边界层影响的范围增大,均方根脉动压力系数整体有增大的趋势;倒锥处,背风面的分离区减小,由此产生的扰动作用减弱,均方根脉动压力系数有所降低。
4)采用优化倒锥型线的设计方式来抑制倒锥部位的脉动压力,分析了四种外形下的时均摩擦力系数、分离区、均方根脉动压力系数,结果表明,“切线弧+圆弧”外形设计最有利于优化其脉动压力环境。
