直升机旋翼涡环状态的气动噪声特性

2023-01-05王亮权徐国华杨仕鹏

空气动力学学报 2022年6期

王亮权，何龙，3，*，徐国华，杨仕鹏，李丹

(1.中国空气动力研究与发展中心旋翼空气动力学重点实验室，绵阳 621000；2.南京航空航天大学直升机旋翼动力学国家重点实验室，南京 210016；3.北京航空航天大学航空科学与工程学院，北京 100191)

0 引言

能够垂直起降是旋翼飞行器所具备的独特优点，自应用伊始，直升机飞行员就发现在做垂直下降或陡下滑飞行时，若操纵不慎，旋翼会陷入一种紊乱的流场之中，致使机身出现剧烈振动、旋翼拉力急剧下降并迅速丢失高度，进一步导致驾驶杆操纵失效。人们根据这种状态下旋翼的流场特征将其形象地命名为“涡环状态”[1]。当直升机旋翼陷入涡环状态时，如果没有及时采取正确的改出措施，可能造成严重的坠地事故[2-3]。

国内外针对直升机旋翼涡环状态开展了一些地面试验[4-10]和飞行试验[11]。在此基础上，一些学者结合理论分析方法[12-13]提出了有关涡环状态速度边界的简单经验判据[14-17]。这些经验判据为避免直升机进入涡环状态提供了有效参考，但不同经验判据的结论并不一致。另外，在下降飞行时依赖过于保守的经验判据也不利于充分发挥直升机的近地机动能力。

除试验研究和理论分析之外，关于旋翼垂直下降和涡环状态的数值模拟研究开展较少，这主要是由于涡环状态下的旋翼尾迹具有强烈的非周期性和不稳定性，开展有效的模拟对数值计算方法有很高的要求。Leishman和Bhagwat[18]尝试使用自由尾迹方法研究涡环状态下旋翼尾迹的不稳定性，但他们基于单根涡线求解的自由尾迹方法无法模拟流场中涡的破碎、融合等复杂效应。Eric等[19]使用几百万数量的嵌套网格进行涡环状态的计算流体力学（computational fluid dynamics,CFD）数值模拟，由于数值耗散较为严重，对旋翼涡环状态的流场细节捕捉存在不足。国内曹栋和曹义华[20]结合动量叶素理论和CFD方法，模拟了旋翼垂直下降状态的空气流动特性，李高华[21]使用高分辨率自适应动态重叠网格方法，研究了旋翼涡环流场中涡环的生成和非对称破缺机理。

直升机在复杂环境空域下降或着陆飞行时，飞行员需要不断观测地形并进行操纵，很难发现旋翼下降率已进入危险的涡环状态范围。尽管涡环状态可能会带来额外的振动，但旋翼飞行器本身振动水平就较高，当飞行员发现座舱振动水平异常时，旋翼可能已经进入了难以改出的深度涡环状态。美国联邦航空局2000年发布的旋翼飞行器操作手册[22]中指出，在进入涡环状态的早期就必须前推驾驶杆让直升机获得前飞速度，同时降低旋翼总距。因此在涡环状态改出策略已明确的前提下，对涡环状态的及时发现和预警[23-25]变成了一个具有重要工程应用价值的课题。

鉴于目前尚无成熟的旋翼涡环状态预警方法，且缺乏关于涡环状态旋翼气动噪声辐射特性的研究，本文基于一种鲁棒的CFD/涡粒子耦合数值模拟方法，针对Caradonna-Tung旋翼[26]（以下简称C-T旋翼）开展了相关模拟研究。以旋翼悬停流场模拟数据为基础，通过逐步增大垂直下降率的方式模拟旋翼涡环状态。在得到不同下降率条件下的旋翼流场数据后，进行了气动噪声声压时间历程和频谱特性分析。基于气动噪声分析结论，创新地提出通过实时采集和分析旋翼垂直下降时的气动噪声信号，对涡环状态的出现进行预警和及时规避的新方法。该方法不需要依赖飞行员的驾驶经验，有望提升直升机做垂直下降等飞行状态时的安全性，并充分发挥其使用效能。

1 数值计算方法

1.1 旋翼流场及气动噪声数值方法

对于直升机旋翼三维流场数值模拟，考虑到可压缩流场仅存在于靠近桨叶尖部的区域，而远离这一区域以外的流场都可以视作是不可压的，因此可以使用基于拉格朗日描述的涡粒子方法[27]模拟旋翼背景流场，以取代重叠网格方法中密集的背景网格，同时仍然使用贴体网格模拟桨叶周围的可压缩流动和非定常气动力[28]。这种耦合策略能够综合CFD模拟桨尖涡生成，并结合涡粒子方法模拟桨尖涡输运的优势，且具备良好的数值稳定性和计算效率。其中，CFD求解有限体积形式的RANS方程，控制方程可表示为：

式中，Ω表示网格控制体，W是控制体上的守恒变量，S 代表控制体的表面，Fc和Fv分别表示控制体的对流通量和黏性通量。采用Roe格式进行控制方程的空间离散，采用LU-SGS格式进行时间离散，湍流模型则使用Spalart-Allmaras一方程模型。

基于拉格朗日描述的涡粒子控制方程可表示为：

其中，x 为涡粒子的位置矢量，u是粒子的运动速度，ω是粒子的涡量，υ是空气的运动黏性系数，方程（3）右端第一项称为拉伸项，第二项称为黏性扩散项，第三项Sω表示旋翼桨叶产生的涡量源项。对涡粒子控制方程的具体求解算法可参考文献[29]。

CFD/涡粒子耦合方法用于直升机旋翼垂直下降和涡环状态模拟的计算域如图1所示。CFD计算由于受数值稳定性的限制，同时要捕捉桨叶表面的流场细节，需采用较小的时间步，本文计算时取0.5°。而涡粒子计算允许取更大的时间步长，为了便于同CFD区域的信息交换，一般取CFD计算时间步长的整数倍，本文的模拟中取为2.0°。即在每个涡粒子计算时间步中，CFD的求解过程被分解为四个较小的时间步迭代，完成一个涡粒子时间步计算后，CFD和涡粒子计算域进行流场信息交换。CFD计算域向涡粒子计算域传递新生涡的位置及强度，涡粒子计算域则向CFD计算域反馈速度和压力边界条件。从CFD/涡粒子耦合方法模拟得到的旋翼流场中提取数据，作为旋翼气动噪声计算的输入，并基于Ffowcs-Williams和Hawkings推导的FW-H方程[30]进行旋翼气动噪声的求解。忽略FW-H方程中的四极子声源，利用格林函数将微分方程的求解转化为积分方程，可得到FW-H方程的时域求解公式[31]。典型观测位置的噪声时域解可分为厚度噪声和载荷噪声两种成分，对噪声时域信号进行频谱分析，可得到旋翼气动噪声的频谱特征。

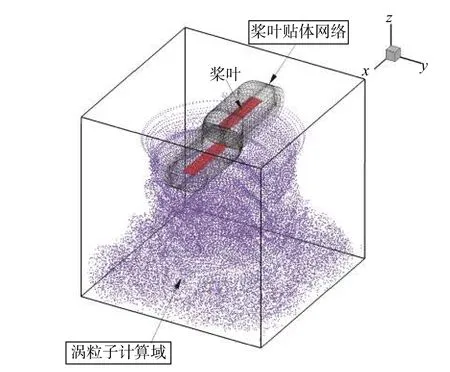
图1 CFD/涡粒子耦合计算域示意图Fig. 1 Schematic of the CFD/vortex particle coupling zone

1.2 旋翼涡环状态模拟策略

由于旋翼涡环状态极不稳定，本文采用由C-T旋翼悬停流场（桨尖马赫数Ma=0.612，总距θ0=8°）开始，逐步提高旋翼垂直下降率从而向涡环状态逼近的数值计算策略。C-T旋翼具有两片桨叶，桨叶半径1.143 m，弦长0.1905 m，使用NACA0012翼型，桨叶无负扭转[26]。旋翼垂直下降率µz使用悬停诱导速度v0无量纲化，其中v0=。涡环状态模拟的具体策略如下：使用计算的悬停流场数据对下降率µz=0.2时的流场进行初始化，以该下降率进行三圈的流场模拟，保存并使用第三圈模拟结束后得到的流场数据初始化下降率µz=0.4的流场，同样计算三圈，以此类推，直到旋翼进入深度涡环状态。

本文计算使用的单片桨叶网格数量约100万，而对于旋翼背景流场的捕捉，需要选择合理的涡粒子数量进行模拟。根据魏鹏等的研究[32]，4万以上的涡粒子可以较好地模拟旋翼悬停流场。考虑到需要在悬停流场的基础上进行旋翼下降状态模拟，本文使用的涡粒子初始数量约7万，在PC上完成一个垂直下降率状态的耦合计算耗时约5.8 h。

2 旋翼涡环状态气动力及流场特性

图2给出了数值模拟得到的C-T旋翼的拉力时间历程，从图中可以看出，旋翼悬停时的初始拉力系数约为0.0043。在小垂直下降率时，旋翼的拉力相对悬停状态略有提升；当下降率达到µz=0.6时，旋翼拉力开始出现较为明显的波动；在µz=0.8时，旋翼拉力波动加剧，但计算三圈之后仍然能保证一定的拉力；当下降率µz≥1.0时，拉力急剧下降，µz=1.2模拟过程中旋翼的平均拉力只有0.0025，相对悬停状态下降了41.8%，旋翼此时早已进入深度涡环状态。在大垂直下降率时，旋翼周围的流场难以保持稳定，十分容易溃散，图3展示了深度涡环状态旋翼周围的代表性瞬时流场。可以看出旋翼周围积聚了大量尺度不均匀且分布不规则的涡，这些涡之间存在复杂的破碎和融合等效应，涡与直升机桨叶之间也会出现强烈的桨-涡干扰现象。从旋翼纵向对称面内的流线图可以看出，大量气流向下通过桨盘后再次回到桨盘上方形成回流，严重降低旋翼产生拉力的能力。

图2 数值模拟过程中C-T旋翼的拉力时间历程Fig.2 Thrust timehistory of the C-T rotor in the numerical simulation

图3 深度涡环状态桨盘周围的代表性瞬时流场(µ z=1.2)Fig.3 Typical instantaneousflow fieldsaround the rotor in the deep vortex ring state(µ z=1.2)

不同垂直下降率状态旋翼桨叶四个展向剖面（图4）的升力系数变化如图5所示，四个剖面离旋翼中心的距离分别为0.68R、0.80R、0.89R和0.96R。从图中可以看出，µz≤0.8时，0.89R剖面的升力系数显著高于其余三个剖面。从图5（c）可以看出，与旋翼的整体拉力系数变化对应，在数值模拟进行到第8圈后，0.80R、0.89R和0.96R三个剖面的升力开始出现较为明显的波动，而0.68R剖面由于更为靠近桨叶内段，升力的波动幅值相对于其他三个剖面较小，从图5（d～f）中也能看出类似的现象。

图4 桨叶展向四个不同的剖面Fig.4 Four spanwise cross sectionsalong the rotor blade

图5 不同垂直下降率下四个桨叶剖面的升力系数变化Fig.5 Variation of lift coefficient at four blade sectionsunder different vertical descent rates

3 旋翼涡环状态的气动噪声特性

在得到旋翼三维流场数据的基础上，选择了三个代表性下降率状态（µz=0.0、0.4、1.0）分析旋翼的气动噪声辐射情况（取相应状态第三圈模拟得到的气动载荷数据）。计算了桨盘下方0.5R处，尺寸为5R×4R的观测平面（图6）上的噪声幅值，观测平面上的计算采样点间距0.25R，采样点数量357个，单个采样点的噪声声压时间历程计算和频谱分析耗时仅需数毫秒。由于旋翼厚度噪声主要沿着桨盘平面内传播，旋翼垂直下降率变化主要影响观测平面上的载荷噪声。从观测平面的载荷噪声分布（图7）可以看出，桨盘正下方存在噪声热区，而从噪声热区向外，噪声幅值逐渐衰减。下降飞行状态下噪声衰减的趋势更为显著，µz=0.4和 µz=1.0两个状态的噪声分布情况十分相似。悬停状态下观测平面内的载荷噪声最大幅值为125.2 dB，而在涡环状态（µz=1.0）下最大噪声幅值为126.4 dB，相对于悬停状态高出1.2 dB，噪声幅值增加并不大。在噪声平面的端点位置，悬停状态对应的载荷噪声幅值约108 dB，而µz=0.4和 µz=1.0两个下降状态该位置处的噪声仅有约100 dB，这可能是由于旋翼有一个较大的向下的运动速度，使得噪声传播更加集中在桨盘正下方的缘故。

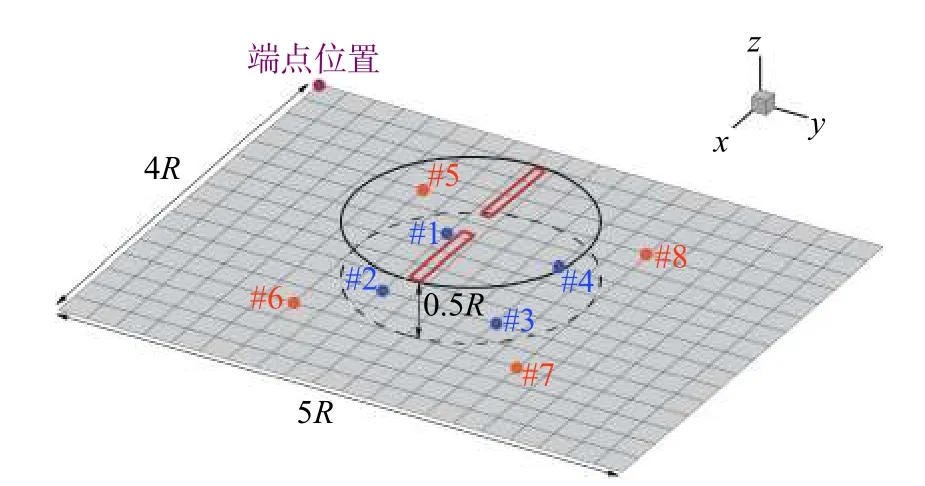
图6 观测点位置示意图Fig.6 Schematic of the observation point locations

图8 给出了三种状态观测平面上最大噪声辐射位置处的声压时间历程和频谱特性（桨叶通过频率BPF=66.2Hz）。可见悬停状态载荷噪声声压波形十分光顺，声压峰值在100 Pa左右。从其频谱图上可以看出，随着频谱阶次的增长，相应阶次对应的噪声幅值下降很快，频谱阶次超过10倍频时，对应的噪声幅值不到50 dB。µz=0.4的下降状态载荷噪声声压时间历程波形相对悬停状态有所不同，声压峰值提高到了120 Pa左右，频谱阶次10到40之间的各阶噪声幅值增加到80 dB左右。而深度涡环状态下的载荷噪声声压呈尖脉冲波形，表现出典型的桨-涡干扰噪声信号特征，声压峰值达到了140 Pa左右；其基频噪声幅值虽然同样保持在120 dB左右，但5～40倍频谱阶次声波对应的噪声幅值却一直处于较高水平，均在100 dB左右。从噪声声压时间历程和频谱分析结果都可以看出，下降状态旋翼气动噪声中的桨-涡干扰噪声成分较为显著。

图7 不同飞行状态的载荷噪声辐射情况Fig.7 Loading noise radiation under different flight states

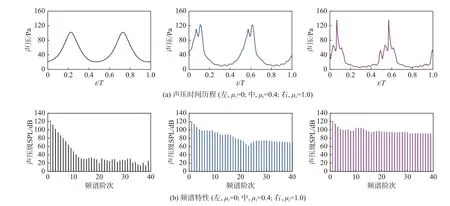
图8 不同飞行状态的载荷噪声特性（最大噪声位置）Fig. 8 Loading noise characteristics under different flight conditions(peak noiselocation)

图9不同飞行状态的载荷噪声特性（端点位置）Fig. 9 Loading noise characteristics under different flight conditions(endpoint location)

图9 给出了观测平面端点位置处的载荷噪声对比结果。该位置对应的悬停噪声波形具有类似于正弦曲线的特征，声压的正负峰值相近，均在9 Pa左右；而小速度下降（µz=0.4）和深度涡环状态（µz=1.0）观测到平面端点位置处的噪声波形负峰值很小，正峰值也小于悬停状态，幅值减小到了约6 Pa。从频谱分析结果上看，悬停状态下的基频噪声幅值略高于小速度下降和深度涡环状态，但当频谱阶次达到20时，悬停噪声对应的幅值很小（仅为20 dB左右），而小速度下降时该频谱阶次对应的噪声幅值仍有约60 dB，深度涡环状态下更是达到了80 dB左右。

为比较涡环状态下不同时刻的旋翼气动噪声辐射特性，图10给出了观测平面上八个观测点处的声压时间历程（#1、#2、#3、#4为一组，#5、#6、#7、#8为一组，每组四个观测点与桨盘中心的距离相等），可以看出两组观测点噪声波形和峰值均存在一定差异，这反映了涡环状态旋翼流场和噪声传播的非周期性。表1给出了相应观测点处计算得到的噪声幅值，观测点#2和#3相差达1.4 dB，观测点#7和#8相差达1.8 dB。图11给出了观测点#1、#2、#3、#4噪声的频谱分析结果，可以看出尽管四个位置的噪声声压波形存在差异，但噪声频谱分布结果却较为相似。

图10 涡环状态不同观测点载荷噪声声压时间历程Fig.10 Time history of loading noise pressure at different observation points in the vortex ring state

表1 不同观测点噪声幅值Table 1 Noise level at different observation points

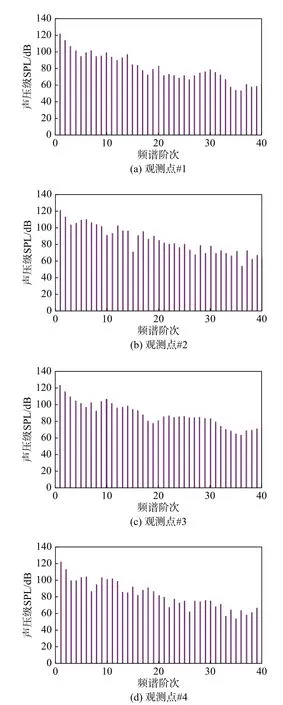
图11 涡环状态不同观测点载荷噪声频谱分析结果Fig.11 Spectral analysisresult for the loading noise at different observation pointsin the vortex ring state

4 基于气动噪声监测的旋翼涡环状态自动预警方法

旋翼涡环状态的高度危险性决定了对其进行预警极为重要。在进入涡环状态的早期，旋翼流场紊乱程度有限，驾驶杆的操纵功效损失也并不严重，直升机飞行员可以通过向前推驾驶杆让直升机尽快转入前飞，使旋翼脱离涡环状态[33]。本文的数值模拟结果表明，下降状态时桨叶通过频率为10倍频以上的载荷噪声（桨-涡干扰噪声成分）幅值会有所提高，下降率越大这种增大趋势越显著。这意味着可以在直升机机身上安装麦克风（如图12所示），通过实时监测并分析旋翼辐射的气动噪声信号来对涡环状态进行预警[34]。