针对高阶DG数值格式的非定常流场预测建模

丁子元，安 慰，刘学军，吕宏强

(1.南京航空航天大学计算机科学与技术学院，模式分析与机器智能工业和信息化部重点实验室，南京 211106；2.空气动力学国家重点实验室，绵阳 621000；3.气动噪声控制重点实验室，绵阳 621000；4.软件新技术与产业化协同创新中心，南京 210023；5.南京航空航天大学航空学院，南京 210016)

0 引言

近三十年来，随着计算能力和数学算法的进步，CFD计算技术取得了长足发展，基于数值模拟技术的设计和优化也日益普及，然而非定常流场的高精度求解计算过程极其耗时，是一个亟待解决的问题。高阶间断伽辽金方法（high-order discontinuous Galerkin,DG）可以在任意几何形状的单元获得高阶精度，被认为是解决这一问题最有前途的技术之一[1]。但是该方法增加了单元内部插值函数的阶数，也提高了单个单元的实际计算量和存储量。总体而言，虽然得到同等精度数值结果的情况下，高阶间断伽辽金所需的未知数自由度较有限体积法要少得多，但长时间的非定常计算量仍然很大。

许多研究者希望通过降阶模型（reduced order models,ROMs）来提高计算效率，比如动态模态分解（dynamic mode decomposition,DMD）方法[2]、库普曼算子（Koopman operator）方法[3]和适用于复杂的高维度的系统降维提取流场主要特征的本征正交分解（proper orthogonal decomposition,POD）方法[4]。但是边界条件、雷诺数等真实流场状态对于这类方法的模型精度影响很大，降阶模型欠缺鲁棒性，并不适合应用于所有条件下的流场[5]。

机器学习方法可以捕获流体力学中主要的动态特性，近年来相关研究取得的进展也证明了其能够作为流场预测的一个有力工具[6-9]。深度学习技术在近些年被广泛关注和应用，其不仅能够挖掘大量数据的内在规律，而且能够构建不同变量之间的非线性映射关系，是一种高效的函数逼近技术。近年来，深度学习在自然语言处理[10]、医疗诊断[11]、图像检测与识别[12]等相关领域都取得了突破性进展。更有研究者将深度神经网络应用在基于雷诺平均模拟（Reynolds average Navier-Stokes,RANS）的湍流建模[9,13-14]以及基于大涡模拟（large-eddy simulation,LES）的亚格子应力项建模[15-16]。这些尝试是对湍流模拟中的某些应力项进行参数化建模，能够通过深度神经网络提高计算精度，在一定程度上缓解耗时计算的压力，但往往会忽略非定常流场的时空特征对建模的重要性。

通过提取输入流场的时间以及空间特征来预测未来时刻的流场可以看作是视频帧的预测。视频预测通过对视频场景的建模帮助机器完成决策，虽然当前的研究还处于早期阶段，但是文献[17-20]利用生成对抗网络、卷积神经网络等方法对这一问题进行了探索，证明了深度学习技术具备学习并预测时空序列信息的潜力。

有研究者将上面提到的相关技术成功应用于流场预测。Lee等[21]将基于质量和动量守恒的损失函数加入到神经网络中，运用生成对抗网络（generative adversarial networks,GAN）等四种不同的方法预测了不同雷诺数下的非定常流场。Han等[22]构建了一个由卷积神经网络（convolutional neural networks,CNN）、卷 积 长 短 期 记 忆 网 络（convolutional long short term memory neural network,ConvLSTM）和反卷积神经网络（deconvolutional neural network,DeCNN）组成的混合神经网络结构，降低了非定常流场维度并且捕获到动态时空特征，成功预测了不同工况下未来时刻的流场。文献[23]提出一种改进的生成对抗网络，可以生成给定时间状态下的非定常周期性流场预测结果。然而上述工作存在局限性，即训练样本是由计算网格上有限个采样点上的物理量构成，若要得到流场中所有位置的物理量，一般采取的是插值方法，这会造成潜在误差。

以上工作均将流场作为图像来处理，区别于之前的工作，本文基于高阶间断伽辽金方法的隐式大涡模拟（implict large eddy simulation,ILES）求解过程，提出一个全新的建模思路，将求解中产生的高阶多项式系数（即高阶间断伽辽金方法的原始变量）依据网格单元的空间相邻关系排列，并按照时序关系组成序列数据。具体来说，基于高阶间断伽辽金方法的原始数据结构构建了一种可行的新型深度神经网络，通过直接预测非定常的高阶多项式系数（即原始未知数）得到全息的非定常流场。本文首先给出了混合深度神经网络的结构设计，然后介绍了针对高阶间断伽辽金数据结构的样本集构造、训练和测试结果。最后给出了结论和展望。

1 混合深度神经网络

1.1 整体结构设计

为了利用深度神经网络捕捉到高雷诺数下非定常流场内隐含的时空特征，并以此来预测未来时刻的流场状态，我们设计了一个由三维卷积、残差网络和通道级别注意力机制三大模块组成的新型深度神经网络，如图1所示。

其中，三维卷积模块由三个三维卷积层组成，通过三维滤波器与时间上连续的多个帧组成的立方体进行卷积操作，从而获取到相邻帧之间的时间特征。在进行二维残差模块之前，需要先将上一个模块的输出矩阵重塑为残差模块的输入矩阵所对应的维度，然后通过由六层残差网络堆叠而成的残差网络模块进一步提取特征表示之间的空间相关性。需要注意的是，在提取空间特征时没有涉及任何下采样或者池化操作，因为这些操作会导致张量的尺寸变小，从而使网络对空间特征不敏感[24]。最后，为了识别和量化特征在局部空间中作用的不同程度，我们引入一个通道级别的注意力机制模块，自适应地重新调整每个通道的重要程度，进一步提升性能，且保证最终的预测值和网络的输入有相同的维度。下面将对构成深度神经网络整体结构的三大模块及其作用进行详细阐述。

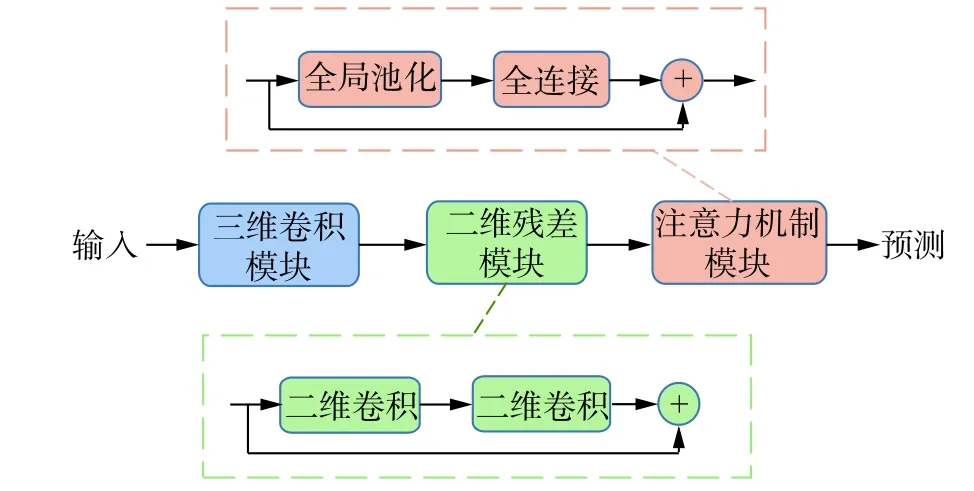
图1 深度神经网络结构Fig. 1 Structure of the deep neural network

1.2 三维卷积模块

三维卷积最早是被提出并应用于识别人体运动行为[18]，因为它可以从多个连续的相邻帧之间捕获隐含的动态信息，所以在视频理解领域，也能够帮助机器更好地学习到数据中包含的时序信息，发现视频帧前后之间的相关性。

三维卷积作用于由多个相邻帧堆叠在一起形成的立方体，然后在这个立方体中利用三维卷积核进行计算。如图2所示，左侧一列在时间上是连续的，右侧的每个特征图与上一层中两个相邻帧相连，且特征图中每一位置处的值，都是通过与上一层三个连续帧的同一处的感受野经过卷积操作之后所得，以此捕捉动态信息。在本文的深度神经网络中，位于第i层第j 个特征图上的点（x,y,z）处的值，其数学表达式为：

图2 三维卷积Fig.2 Three-dimensional convolution

上式中的W、H、D分别表示三维卷积核中的宽度、长度、高度三个维度的大小，tanh是非线性激活函数，是连接到上一层中第 k个特征图的三维卷积核中的(w,h,d)位 置处的值，bij代表偏置参数。

假设图1的三维卷积模块中，总共堆叠了Lc个三维卷积层，下面列出两层之间的数学表达式：

其中，x(l-1)为第l 层的输入，⊗是对应的三维卷积操作，Wl和Bl分别表示三维卷积核以及偏置参数。

1.3 残差网络模块

残差网络可以很好地解决网络退化问题。在三维卷积模块充分提取时间维度上的信息之后，我们采取了文献[25]中提出的一种不会给网络增加额外计算量、更加容易训练的残差网络结构。

如图3所示，每一个残差模块由两个激活函数和两个二维卷积操作构成，将残差单元中的映射表示成f ，并且在三维卷积模块之后堆叠Lr个残差单元，形式上为：

其中，θl表示第l个残差单元中所有可供学习的参数的集合， x(Lc+l-1)是 第l个残差单元的输入。

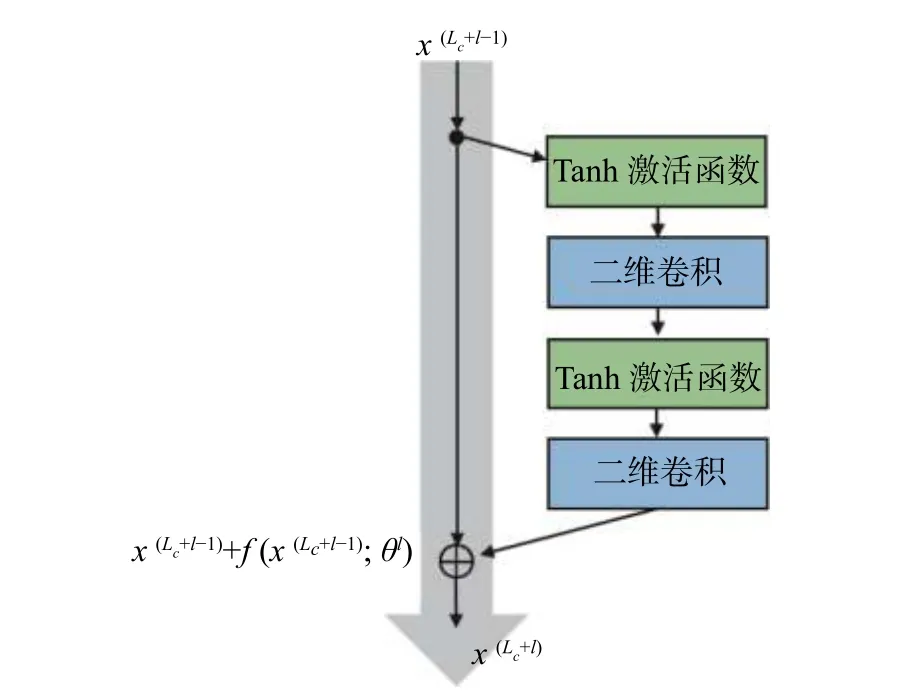
图3 二维残差模块结构Fig.3 Structureof the two-dimensional residual module

1.4 注意力机制模块

注意力机制的灵感来源于对人类视觉的研究，也就是将有限的视觉信息处理资源优先分配给关键的部分，并忽略掉不相关的信息。

在本文中，为了进一步提升模型的能力，一个叫做SENET（squeeze-and-excitation networks）的软注意力机制模块[26]（如图4）被我们嵌入到整体网络结构的最后一部分，用于探索并自动量化通道级别上的特征对于每个区域的贡献程度。

图4 注意力机制模块结构Fig.4 Structure of the attention mechanism module

2 实验设计

2.1 隐式大涡模拟的高阶间断伽辽金求解

非定常可压缩N-S方程形式如下：

二维情况下守恒变量U为：

其中，ρ表示密度，u和 v表示速度的正交分量，E代表单位总能量。

本文采用高阶精度间断伽辽金法[27]对两种不同工况下的二维圆柱绕流进行ILES数值模拟。算例1工 况 为Re=3 900,Ma=0.2，α=0°；算 例2为Re=2×104,Ma=0.2，α=0°。计算域的划分采用了结构化网格，计算网格如图5所示。在网格单元内部用高阶多项式对守恒变量进行表达：

其中， uj(t)为 高阶系数形式的原始变量，ϕj(x)为对应的基函数，N是对应阶数的基函数个数。

首先采用间断伽辽金法对N-S方程进行空间离散，本文采用BR2格式[28]，得到如下离散形式：

其中，Θ=∇U为 引入的辅助变量，F包括对流项和扩散项。Ωe表示单元， ∂Ωe表示单元Ωe的边界，n表示单元边界 ∂Ωe的外法矢。

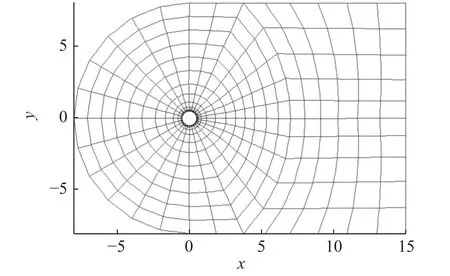
图5 计算网格示意图Fig.5 Schematic of the computational grid

整个离散系统可简写为如下形式：

其 中，u=[u1,u2,···,uk,···,uNele]T是 全 局 自 由 度矢量，uk代表单元k 的自由度，具体表示为uk=其中下标Nele代表全局单元的个数，下标Ne、Nd分别表示单元内方程个数和每个变量的自由度。R(u)=[R1,R2,...,Rk,···,RNele]T为全局残值矢量，Rk代表单元k的残值矢量，M为全局的质量矩阵。

然后进行隐式时间离散，残值项取tn+1时间步变量进行计算，并对式（9）采用向后欧拉差分法，得到如下形式：

定义tn+1步 的非定常残值Re为：

在每个时间步tn+1采用牛顿迭代方法进行求解，直到残值 Re(uk)→0。具体步骤如下：

得到上式中的原始变量uj(t)之后，代入公式（6）得到流场中每个单元内的物理量，即可获得全息流场信息。

2.2 样本集的构造

我们的工作目标是利用计算机视觉领域的先进方法结合间断伽辽金法数据结构的特点，通过先前时间段内的流场信息来预测未来时刻的流场。此处需要特别指出的是本文预测的对象为高阶间断伽辽金数值格式的原始变量，而非前人工作中广泛应用的图像形式。

首先以Re=3 900的圆柱绕流算例为例，详细阐述深度学习数据集的构造，且在所有的实验中，流场数据的生成方式、数据集的构造方式都相同。

由于深度神经网络在图像领域的应用已非常广泛和成熟，因此本文在用于训练以及测试的样本集的构造方面参考了图像数据集的形式。图5是圆柱绕流算例的计算网格，网格总量为476，我们将每一个时刻的流场信息均匀标定在大小为22×26的矩形空间内。在数值模拟实验中，所有的网格都有各自唯一确定的编号，且单元网格为四边形，与之相邻的四个网格（若该网格处于边界，则相邻网格个数小于4）是唯一确定的，所以最终矩形空间的大小由网格单元的数量以及相邻关系唯一确定。如图6所示，每一个小方块类似于像素点，相邻像素点代表相邻的网格单元，其中的数字代表对应的网格单元序号（经过网格单元的重构，图5中的圆柱和网格外围部分退化成了图6右上区域的0号单元区域，不代表任何一个计算网格）。单个时间步内，按如下方法取牛顿法迭代计算所得系数：在每个单元中提取计算守恒变量U（由四个分量组成）所需的插值多项式系数uj(t)(j=1,···,10)，采用三阶格式的情况下每个单元包含40个高阶表达系数。因此采用三维形式的数据22×26×40表示每个时刻的流场信息，最终将数据按照时间顺序排列获得总体数据集。

2.3 模型训练

本文中的两个圆柱绕流算例皆具有准周期性流动的特征，一个周期T内大约有250个时间步求解，其中每个时间步内取7个式（12）～式（15）牛顿迭代步中的收敛结果，即单个时间步内有大小为7×22×26×40的数据作为样本，每一个算例的总体数据集都包含四个周期，由7000个样本组成。

数据归一化是模型训练前的一项基础工作，可以消除维数对预测结果的影响，加快模型的收敛速度[28]。本实验中由于数据本身具有正负属性，为了防止数据特性的丢失，没有采取Min-Max归一化或Z-score归一化，而是将所有用作神经网络输入的样本都在[-1,1]范围内进行缩放。

本文通过最小化损失函数训练深度网络模型，损失函数采用了L1损失和L2损失结合的形式，数学表达式为：

其中，N为训练数据个数，∧y为预测的值，y为通过流场求解器计算所得的对应真实值。利用自适应矩估计[29]和反向传播算法[30]对网络进行训练。前者可以根据训练数据迭代更新神经网络权值；后者是一种广泛使用的参数学习方法，它通过误差反向传播校正每个神经元的权值，最终通过最小化损失函数来得到最优的参数。

深度神经网络的结构参数见表1，其中三维卷积部分的填充方式选择的是“SAME”。在时间维度上，三维卷积层1、2、3的卷积步长分别为1、2、1，根据式（17）特征图大小的计算方法，得到了如表1所示信息。

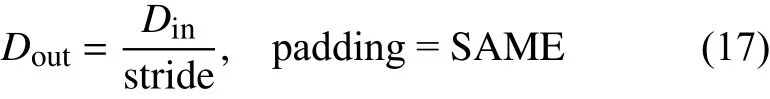
图6 网格相邻关系Fig.6 Neighboring relationship of the grids

需要特别指出的是，隐式时间离散过程中式（9）中的全局自由度矢量 u在 时间步tn+1可以表示为：

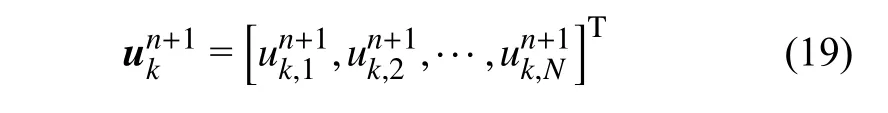
因为计算网格总量为476，本文采取三阶格式，所以上式中 Nele=476 ， N=40。从式（12）～式（15）可以发现时间步tn+1时 刻的uk+1只与u0和uk这两个变量相关。为了和数值模拟过程中流场原始变量的产生保持一致性，混合深度神经网络将u0和uk叠加作为输入，即经过样本集构造输入数据尺寸为22×26×40×2， 模 型 的 输 出 为 时 间 步tn+1时 刻 的uk+1， 数据尺寸为 22×26×40。

表1 深度神经网络结构以及参数设置Table 1 Structureand parameter setting of the deep neural network

优化后的模型能够代替隐式大涡模拟的高阶间断伽辽金求解过程中复杂的空间离散和隐式时间离散计算过程。本文利用训练好的网络来实现动态预测，将预测结果转化为高阶系数，然后代入公式（6）可计算出流场中任意单元内的物理量，从而得到全息流场信息。随着时间的推进，循环地将预测的结果作为下一次的输入，因此网络可以在未来时刻流场未知的情况下，通过前面时间段内已知的流场来完成预测。

2.4 整体工作流程

图7展示了所发展方法的整体工作流程图。对2.1节中所要求解的控制方程进行隐式大涡模拟。首先利用间断伽辽金法对N-S方程进行空间离散，然后采取隐式时间离散方式完成非定常时间推进。其中单个时间步内采用牛顿法进行迭代计算，由此产生的大型线性系统利用预处理的GMERS方法计算，从而得到训练所需的数据，即高阶表达系数。值得注意的是，相应单元上构造出来的高阶函数可以表征网格内任一点的流场信息。按照2.2节中的描述完成样本集的构造，之后训练神经网络直至满足精度要求为止。

下面的章节中，我们将利用两个不同来流工况的算例对所提出方法的准确性及泛化性进行讨论。

3 实验结果及分析

为验证本文所提出的深度神经网络的预测准确性，我们首先利用Re=3 900 、Ma=0.2、α=0°工况下隐式大涡模拟的高阶间断伽辽金方法求解所得的数据对网络进行离线训练。然后用优化完之后的模型进行动态预测，将先前时间步下预测出的流场数据放到输入中，实现递归预测接下来时间步的流场。最后将其预测结果与CFD计算结果做对比。图8～图10分别是紧接着训练所用数据50个时间步之后、100个时间步之后、200个时间步之后的流场情况对比。图11和图12分别是三个时间节点下Ma和 p的预测误差展示图，对比之后发现混合深度神经网络预测结果与CFD计算结果吻合较好。

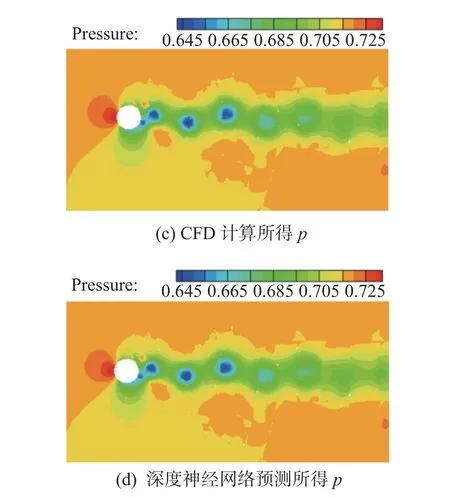
图8 模型预测与CFD计算在50个时间步之后的流场对比（Re = 3 900）Fig.8 Flow field comparison between the modeling prediction and the CFD simulation after 50 time steps (Re = 3 900)

选取如图13所示的两个点P1（1.5，0）和P2（5，0.5）来展示时间序列的预测精度。将深度神经网络在选定位置上预测所得的三个物理量u、v、p和真实样本进行比较，得到结果如图14。其中相对误差曲线图中的纵坐标表示平均百分比误差（mean absolute percentage error,MAPE），表达式如下：

图9 模型预测与CFD计算在100个时间步之后的流场对比（Re = 3 900）Fig.9 Flow field comparison between the model prediction and the CFD simulation after 100 time steps(Re = 3 900)

图10 模型预测与CFD计算在200个时间步之后的流场对比（Re = 3 900）Fig.10 Flow field comparison between the model prediction and the CFD simulation after 200 time steps(Re = 3 900)

图11 Ma 的绝对预测误差（Re = 3 900）Fig.11 Absolute prediction error of Ma between the predicted and CFD results(Re = 3 900)

图12 p 的绝对预测误差（Re = 3 900）Fig.12 Absolute prediction error of p between the predicted and CFD results(Re = 3 900)

图13 计算域中两个指定观测点所处位置Fig.13 Locationsof two specified observation pointsin the computational domain

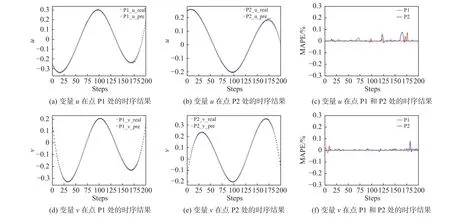
图14 预测过程中两个指定位置处流场变量的演化（Re = 3 900）Fig.14 Evolution of flow field variables at the two specified observation pointsduring the prediction process(Re = 3 900)

为了进一步探索本文所提出模型的泛化能力，我们将神经网络用于预测流动特征更复杂的非定常流场。虽然同样是圆柱绕流，但是该算例具有更高的雷诺数： Re=2×104，Ma=0.2，α=0°。混合深度神经网络预测结果与CFD计算结果的对比如图15～图17所示。图18和图19分别表示三个时间节点下Ma和p的绝对预测误差。可以发现，Ma、p这两个流场变量的预测与CFD模拟流场高度吻合，特别是图15所示较少时间步之后的预测，能够清晰地观测到大尺度涡从物面开始脱落以及尾部区域小尺度结构的耗散。但是随着递归预测过程的推进，来自前面时间步的细微误差将被累积，使得预测结果与真实CFD计算结果相比出现不可避免的差异。例如图16（d）中边界层信息相比图16（c）的真实情况产生了局部细微变化，图17（b）中尾部的涡与图17（a）中同一位置存在很小色差。

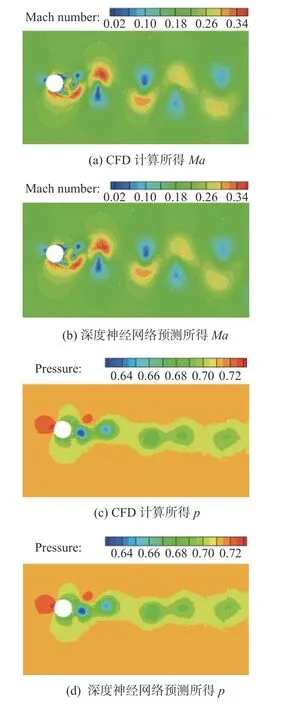
图15 模型预测与CFD计算在50个时间步之后的流场对比（Re = 2×104）Fig.15 Flow field comparison between the model prediction and the CFD simulation after 50 time steps (Re = 2×104)

图16 模型预测与CFD计算在100个时间步之后的流场对比（Re = 2×104）Fig.16 Flow field comparison between the model prediction and the CFD simulation after 100 time steps(Re = 2×104)

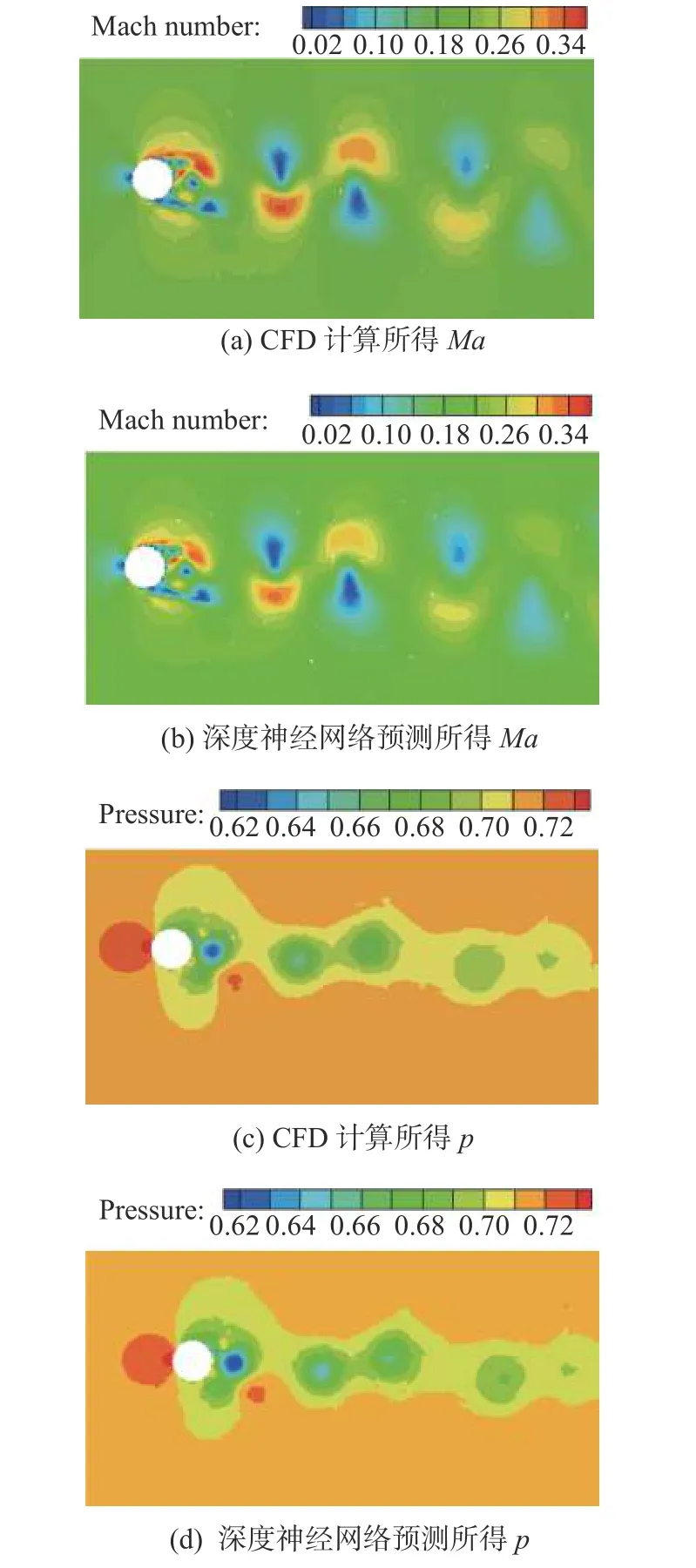
图17 模型预测与CFD计算在200个时间步之后的流场对比（Re = 2×104）Fig.17 Flow field comparison between the model prediction and the CFD simulation after 200 timesteps(Re = 2×104)

将深度神经网络在选定位置上预测所得的三个物理量u、v、p和真实样本进行比较，具体结果展示如图20，所有预测结果与CFD计算结果吻合较好，表明神经网络可以在整体上预测流场特征，而且可以在时空维度上精确地预测流场的变化。

在计算耗时方面，CFD计算以及深度网络训练与测试的具体信息如表2所示（CFD计算的硬件是Intel Xeon E5649 2.53 GHz 4核并行，采用的是并行计算方式；神经网络预测的硬件是Intel Xeon Silver 4210R 2.40 GHz 40核并行，未采用并行计算方式），可以发现在第二个算例中CFD数值模拟一个周期需要7500 s，基于深度学习策略的非定常流场预测方法训练完成之后预测一个周期所需时间为60 s。所有算例中模型预测所需时间降低了两个量级以上，可以显著节约计算成本。

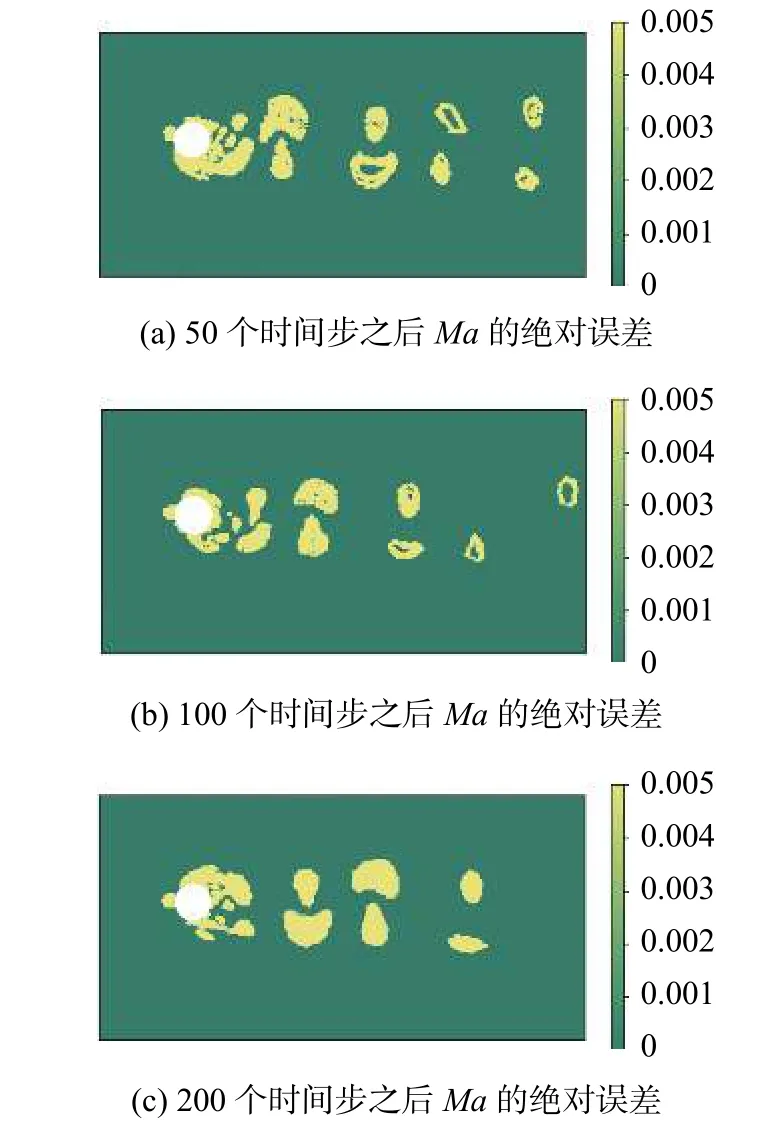
图18 Ma 的绝对预测误差（Re = 2×104）Fig.18 Absolute prediction error of Ma between the predicted and CFD results(Re = 2×104)

图19 p 的绝对预测误差（Re = 2×104）Fig.19 Absolute prediction error of p between the predicted and CFD results(Re = 2×104)

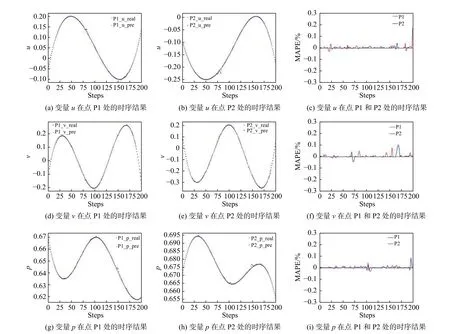
图20 预测过程中两个指定位置处流场变量的演化（Re = 2×104）Fig.20 Evolution of flow field variablesat the two specified observation pointsduring the prediction (Re = 2×104)

表2 CFD计算和深度神经网络训练与测试时长Table 2 Training and testing time of the CFD calculation and the deep neural network modeling

4 结论

目前采用机器学习法预测非定常流场的工作广泛采用图像形式表征流场信息，该路线的优势在于可以充分利用图像处理领域被广泛应用的机器学习方法，缺点在于预测的信息只能用图像表达。区别于已有工作，本文采用机器学习方法直接预测高阶间断伽辽金形式的流场原始变量，保持机器学习模型预测的流场信息形式与CFD方法完全一致。

本文首先针对高阶间断伽辽金的数据特征设计了适用于深度神经网络输入输出的数据结构，然后将三维卷积网络、残差网络、注意力机制相结合，设计了一个新型的深度神经网络。通过对雷诺数3900和雷诺数20000（该工况下的流动具有典型的较复杂多尺度流动特征）下的两个圆柱绕流算例进行数值模拟得到用于训练网络的数据集，将训练完成的网络用于预测未来时刻的流场。将预测结果与直接用CFD求解器计算的结果进行对比，非定常流场预测结果与本文采用的高精度间断伽辽金法流场求解器计算的云图结果高度一致，典型观测点的预测结果与真实结果的平均百分比误差在0.2%之下，反映出本文提出的新型深度神经网络对预测复杂非线性问题的潜力。本文发展的方法优点在于直接预测原始变量而非流场图像，因此获得的是全息的流场信息，但也存在目前普遍都有的长周期预测精度的问题。因此进一步提升小样本量情况下的长周期预测能力是未来研究的一个重要方向。