基于bounding-box与卡尔曼滤波的优化压缩感知算法的目标定位

张小康, 肖本贤, 肖献强,2, 方紫剑

(1.合肥工业大学 电气与自动化工程学院,安徽 合肥 230009; 2.合肥壹恒智能机械人有限公司，安徽 合肥 230000;3.合肥搬易通科技发展有限公司，安徽 合肥 230012)

0 引 言

随着无线通信技术的进步以及无线传感器网络(wireless sensor network,WSN)的广泛应用,精确定位、减小通信开销以及降低节点的能量损耗等成为信号处理领域研究的热点问题。区域的目标精确定位作为无线传感器网络中一个重要研究分支,在军工、航天、石化和建材等领域的室内定位[1]、水体污染定位[2]、位置追踪等诸多场景中得到充分应用,因此提高其定位精度对工业生产和人们日常生活具有重要的实际意义。

近年来,压缩感知(compressive sensing, CS)技术的兴起为目标定位提供了新思路。通过对目标区域进行网格离散化,使得目标位置向量具有天然的稀疏性[3],只需少量的测量信息,便可以通过测量矩阵和测量向量恢复出稀疏信号从而完成网格中多目标的定位。文献[4]将节点之间的连通度作为观测值,通过l1最优化方法从观测向量中重构出目标位置,提高定位精度,但是算法计算量较大;文献[5]利用回溯多分辨率的思想对目标不在网格中心的情况进行网格细分,提高定位精度,但是随着迭代次数的增加计算量大大增加;文献[6]通过LANDMARC结合压缩感知进行室内定位,先利用该算法锁定定位区域,然后利用模拟退火改进的正交匹配追踪算法进行目标位置的定位,兼顾了定位效率和定位精度。通常基于CS的定位方法采用固定的网格划分监测区域[7-9],为了提高定位精度,网格划分宽度应尽量缩小,使得测量矩阵维数急剧上升,压缩感知算法的运算量大大增加。

基于上述问题,本文提出一种优化压缩感知算法,引入bounding-box方法减小未知节点的定位区域,降低测量矩阵维数,从而减小后一阶段压缩感知算法的计算量。利用卡尔曼滤波对同一传感器节点采集到的多个接收信号强度值进行处理,保证观测向量y的准确性,解决了测量向量受噪声干扰导致压缩感知重构精度低的问题。另外针对压缩采样匹配追踪算法(compressive sampling matching pursuit,CoSaMP)候选集冗余度大的缺点提出基于原子相关度阈值的回溯匹配追踪算法,将候选集中的2K个原子相关度的平方平均值作为阈值对候选集进一步筛选,找出相关度较大的原子,避免过多无关原子进入支撑集增加裁剪负担,并在支撑集保留系数较大的原子使得算法以更高的概率获得真正的支撑集,提升重建精度。

1 CS定位模型

基于CS的目标定位模型如图1所示,在无线传感器网络待定位的区域内部署K个可以发出无线电位置未知的目标节点、M个位置已知的传感器。将待定位的区域划分为数量为N的大小均匀的网格,目标位置便离散在这些网格中,这样就将目标的定位问题转化为基于网格的定位问题,通过传感器接收到的信号强度确定目标节点所在的网格位置。

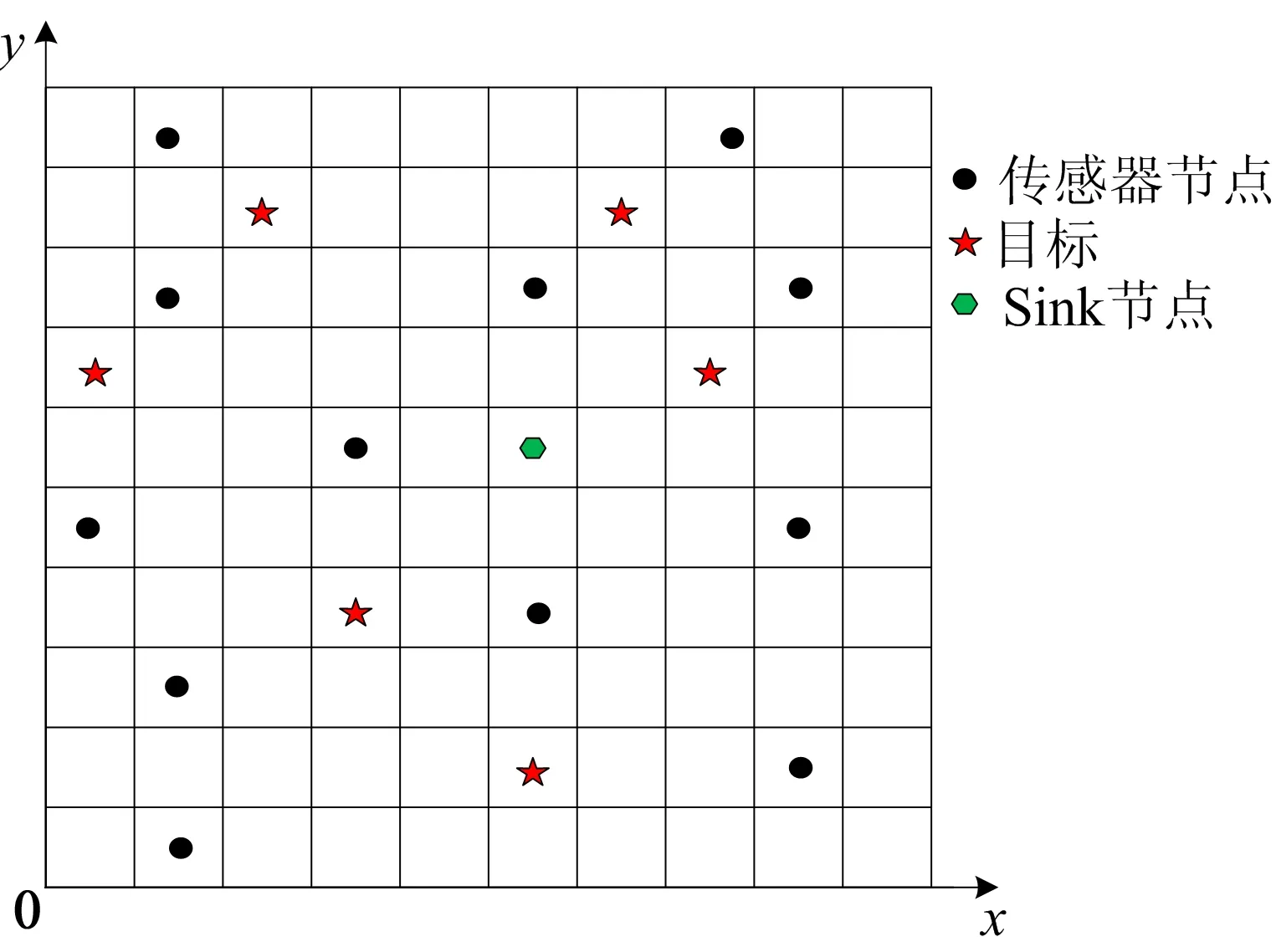
图1 基于CS的目标定位模型

定位区域内M个传感器通过接收信号强度衰减模型获得的观测矩阵P=(Pij)M×N,其中Pij表示第i(1≤i≤M)个传感器到第j(1≤j≤N)个网格的接收信号强度值。传感器接收到目标的信号强度值模型[10]如下:

(1)

其中:d0为参考距离,一般取1 m;P0为在参考距离d0处的接收信号强度;n1为路径衰减指数,一般取2～5;d为传感器到目标的距离;Xσ为高斯噪声变量。

M个位置已知的传感器节点获得K个未知节点的接收信号强度总和得到观测向量y=Pμ,然后将其传送到数据融合中心的sink节点,sink由观测向量y和观测矩阵P重构出稀疏信号μ,信号中系数不为零元素的位置对应着网格中目标所在的位置。

2 基于优化压缩感知算法的目标定位

基于优化压缩感知算法目标定位的流程图如图2所示,整个过程主要由如下3个步骤组成:① 利用bounding-box算法进行区域锁定并获取测量矩阵;② 对传感器节点接收到的接收信号强度值进行卡尔曼滤波处理,构建观测向量;③ 根据获得的测量向量和测量矩阵,采用基于原子相关度阈值的回溯匹配追踪算法进行位置估计。

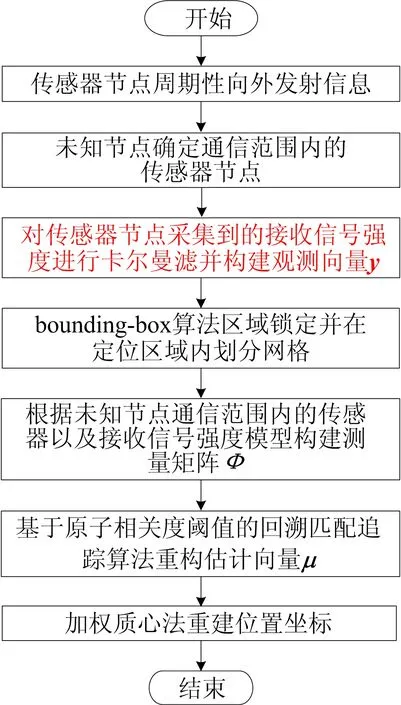
图2 定位流程图

2.1 卡尔曼滤波

观测向量y是传感器节点接收到的未知节点的接收信号强度,决定压缩感知算法的重建精度。在实际测量中因受环境因素的影响,传感器节点的接收信号强度测量值包含数量较小,幅值较大的测量误差。为了保证测量向量的准确性,本文采用卡尔曼滤波对来自同一未知节点多组接收信号强度值进行处理,过滤较大的噪声,使优化后的接收信号强度值更加接近真实值。

卡尔曼滤波是基于线性最小均方误差预测和线性递归更新的优化算法[11]。卡尔曼滤波主要分为预测和更新2个阶段。

(1)预测阶段。t时刻状态预测方程为:

X(t|t-1)=AX(t-1|t-1)+BU(t)

(2)

其中:X(t|t-1)为t时刻的接收信号强度状态预测值;X(t-1|t-1)为t-1时刻的接收信号强度状态值;A为状态转移矩阵;B为控制矩阵;U(t)为状态控制量。在理想状态下,来自同一未知节点的接收信号强度是相同的,因此在实验中A取1,控制量BU(t)取0。

协方差预测方程为:

P(t|t-1)=AP(t-1|t-1)AT+Q

(3)

其中:P(t|t-1)为对应X(t|t-1)的系统误差协方差;P(t-1|t-1)为对应X(t-1|t-1)的系统误差协方差;Q为状态噪声协方差,在实验中,认为预测模型很可靠,因此Q设为1×10-6。

卡尔曼增益为:

K(t)=P(t|t-1)HT(HP(t|t-1)HT+R)-1

(4)

(2)更新阶段。t时刻状态更新方程为:

X(t|t)=X(t|t-1)+

K(t)(Z(t)-HX(t|t-1))

(5)

协方差更新方程为:

P(t|t)=(I-K(t)H)P(t|t-1)

(6)

其中:R为测量噪声协方差;K(t)为t时刻的卡尔曼增益;Z(t)为t时刻的接收信号强度测量值;H为观测状态转移矩阵,传感器节点实际测量的接收信号强度与理想的接收信号强度应该是相同的,因此H取1。

2.2 bounding-box算法获取定位区域

假设待定位目标T通信范围内有3个传感器节点S1、S2、S3,坐标分别为(x1,y1)、(x2,y2)、(x3,y3)。bounding-box算法以及网格划分示意图如图3所示。根据节点通信范围可以获得3个正方形区域,目标就落在这3个矩形的重叠区域,目标T通过通信范围内锚节点获得的定位区域如图3中阴影所示。定位区域的数学表达式为:

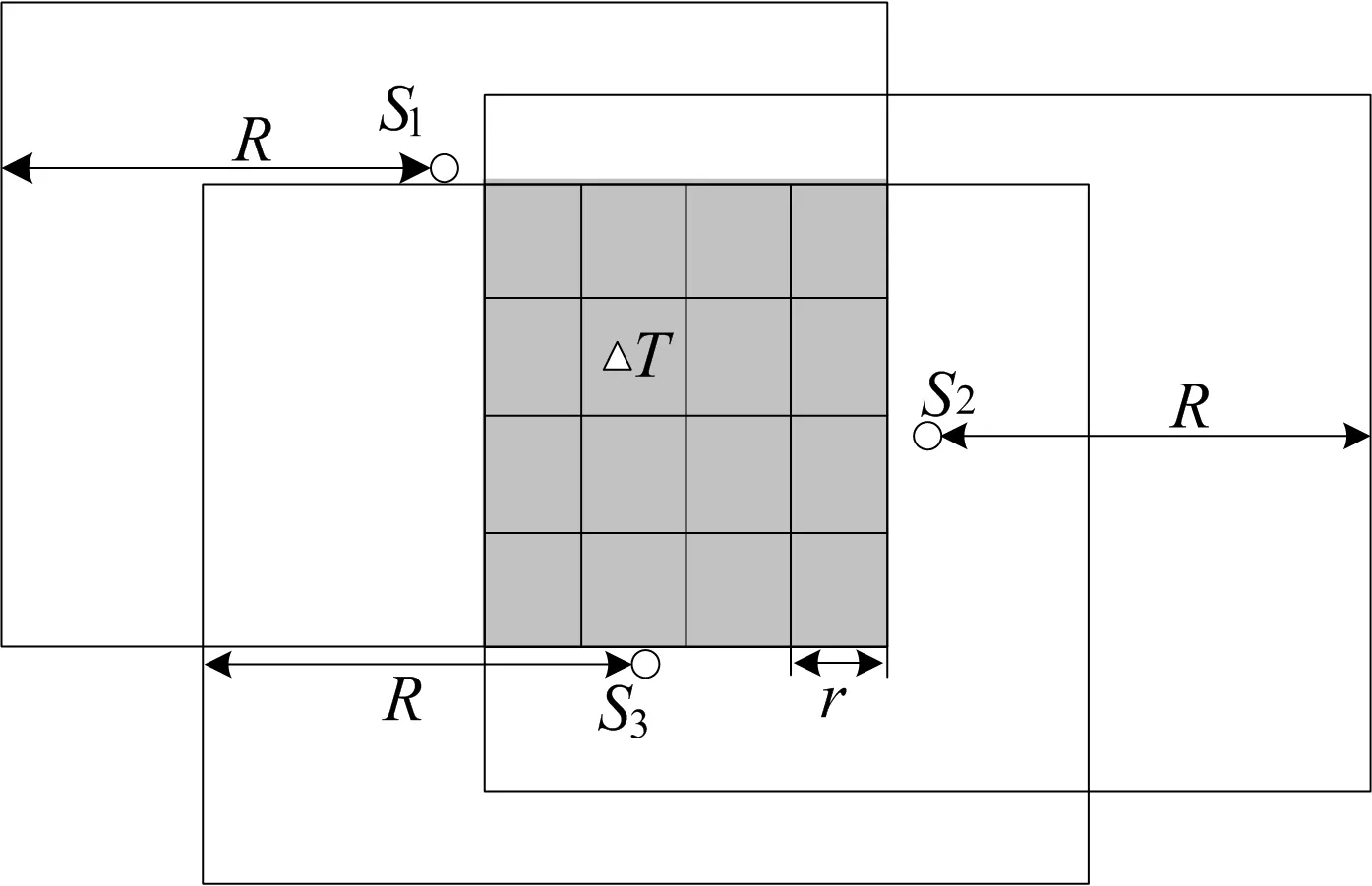
图3 bounding-box算法以及网格划分示意图

(7)

其中:xl、xr、yu、yd分别为重叠区域的左边界、右边界、上边界和下边界；R为节点的通信半径。

将未知节点通信范围内的锚节点作为传感器,根据传感器接收到定位区域内各网格中心的信号强度建立测量矩阵，即

(8)

其中:Pij为第i(1≤i≤M)个传感器节点到第j(1≤j≤N)个网格中心的信号强度由(1)式计算;M为未知节点通信范围内的传感器节点数目;N为网格划分数量。文献[12]表明测量矩阵应当满足:

M≥O(Klg(N/K))

(9)

其中，K为1。因此可以得到:

M≥ClgN

(10)

由此可以推出:

N≤10M/C

(11)

其中:C为测量常数,当网格数N满足(11)式时,压缩感知算法能够精确重建稀疏信号。

在网格定位中感知矩阵列之间相关性较强,无法满足RIP性质[13],需要对测量矩阵P进行预处理才能保证压缩感知算法精确重构。本文采用基于LU分解[14]的方法将原子字典分解为P=LU,然后对观测值y进行下面的变换得到新的观测值y′为:

y′=(L)+y==L+LUμ=Uμ=Φμ′

(12)

其中:L+为L的伪逆;Φ由U列单位化得到,是一个部分正交矩阵,完全满足RIP性质。

2.3 压缩感知算法定位

经过bounding-box算法的区域锁定,目标定位问题转化为1稀疏度的向量的重建问题。稀疏向量重建模型为:

yk=Φμk′

(13)

其中:yk为第k(k≤K)个目标的M×1维观测向量;Φ为经过LU分解的测量矩阵;μk为第k个目标的位置向量,不为0的位置代表可能存在目标的网格。

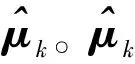
(14)

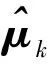
(15)

进一步有:

(16)

利用加权质心算法求解待定位目标位置如下:

(17)

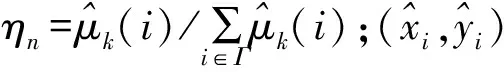
2.4 基于原子相关度阈值的回溯匹配追踪算法

定义原子相关度如下:

u=|ΦTr|

(18)

其中:ΦM×N为测量矩阵;rN×1为残差;u为N×1维的向量,向量中的系数代表ΦM×N中的列和残差r的内积,称为原子相关度。

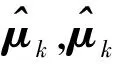
(19)

其中:ui(1≤i≤2K)为原子相关度,由(19)式计算得到。然后根据Υ确定筛选后的候选集λt为:

λt={i||ui|≥Υ}

(20)

每次迭代中,原子相关度阈值Υ随着原子相关度向量u的变化而变化,但总能保留相关度较大的原子,这样既能保证候选原子的可靠性,又能为最终原子集的确定节省时间。

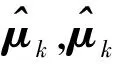
算法的具体步骤如下。

输入:M维测量向量y,M×N维传感矩阵Φ,目标数K,迭代停止阈值Δ。

(1)初始化选取迭代次数t=1,初始支撑集大小为I=K,残差r0=y,迭代停止阈值Δ,初始支撑集F0=∅,支撑集大小Q=δ。

(2)通过u=|ΦTrt-1|计算相关系数u,并从u中取出2K个最大值对应的索引值构成集合T。

(3)在集合T中的2K个原子中求满足|ΦTrt-1|>Υ的原子脚标集合，即

λt=|〈rt-1,Φj〉|>Υ,j=1,2,…,2K。

(4)将挑选出来的原子加入支撑集。计算公式为:

Ft=Ft-1∪λt,Φt=Φt-1∪Φλt。

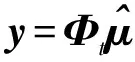
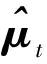
3 实验分析

3.1 仿真环境设置及参数设定

在48 m×48 m的待定位区域内,每隔6 m的间隔均匀布置传感器节点,共形成81个锚节点,K个未知节点随机分布在区域中的任意位置。M为未知节点通信范围内的传感器数量,取决于通信半径R,未知节点根据通信范围内的传感器节点利用bounding-box算法确定定位区域,网格数量N由网格步长r确定。根据已有经验[15-16],并结合本文仿真场景,测量常数C取7,网格划分步长r取2 m,节点通信半径R取20 m,迭代停止阈值Δ设为1×10-6,重构稀疏度δ取4。在仿真实验中加入高斯白噪声来模拟实际环境中的噪声。为了验证本文算法的定位性能,将本文算法与正交匹配追踪算法(orthogonal matching pursuit,OMP)、贪婪匹配追踪算法(greedy matching pursuit,GMP)以及压缩采样匹配追踪算法进行比较。采取传统压缩感知算法定位将整个定位区域划分为20×20的网格,每隔6 m布置传感器节点,共81个传感器节点,未知节点随机分布在网格区域内。为了避免实验受到随机性的影响,每次实验均仿真300次取其平均值使结果稳定。

为了评估定位性能,设第i次定位误差为:

(21)

总的平均误差为:

(22)

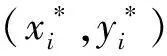
平均定位时间设为:

(23)

其中:K为目标数;Ti为第i次的定位时间。

定义定位成功率为:

(24)

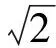
仿真参数见表1所列。

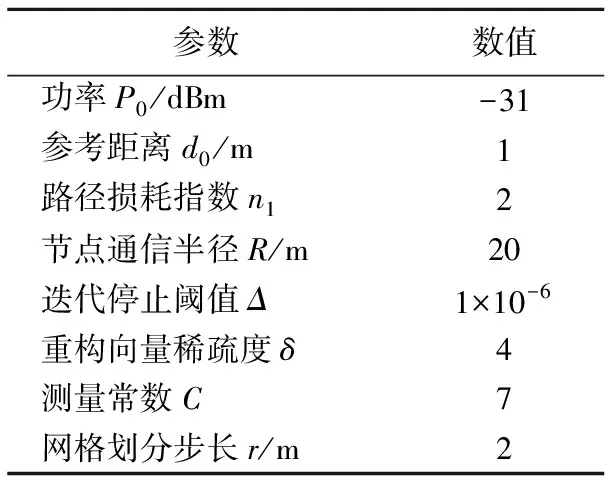
表1 仿真参数

4种算法在K=8、RSN=25 dB时的定位结果对比如图4所示。从图4中可以看出,OMP算法定位效果最差,大多数重建位置距离原始位置较远,定位误差达到2 m以上；CoSaMP算法和GMP算法定位效果优于OMP算法,定位误差分别为1.3、1.5 m;本文算法定位效果最好,重建位置与原始位置几乎重合,平均定位误差为0.71 m,远小于对比算法。

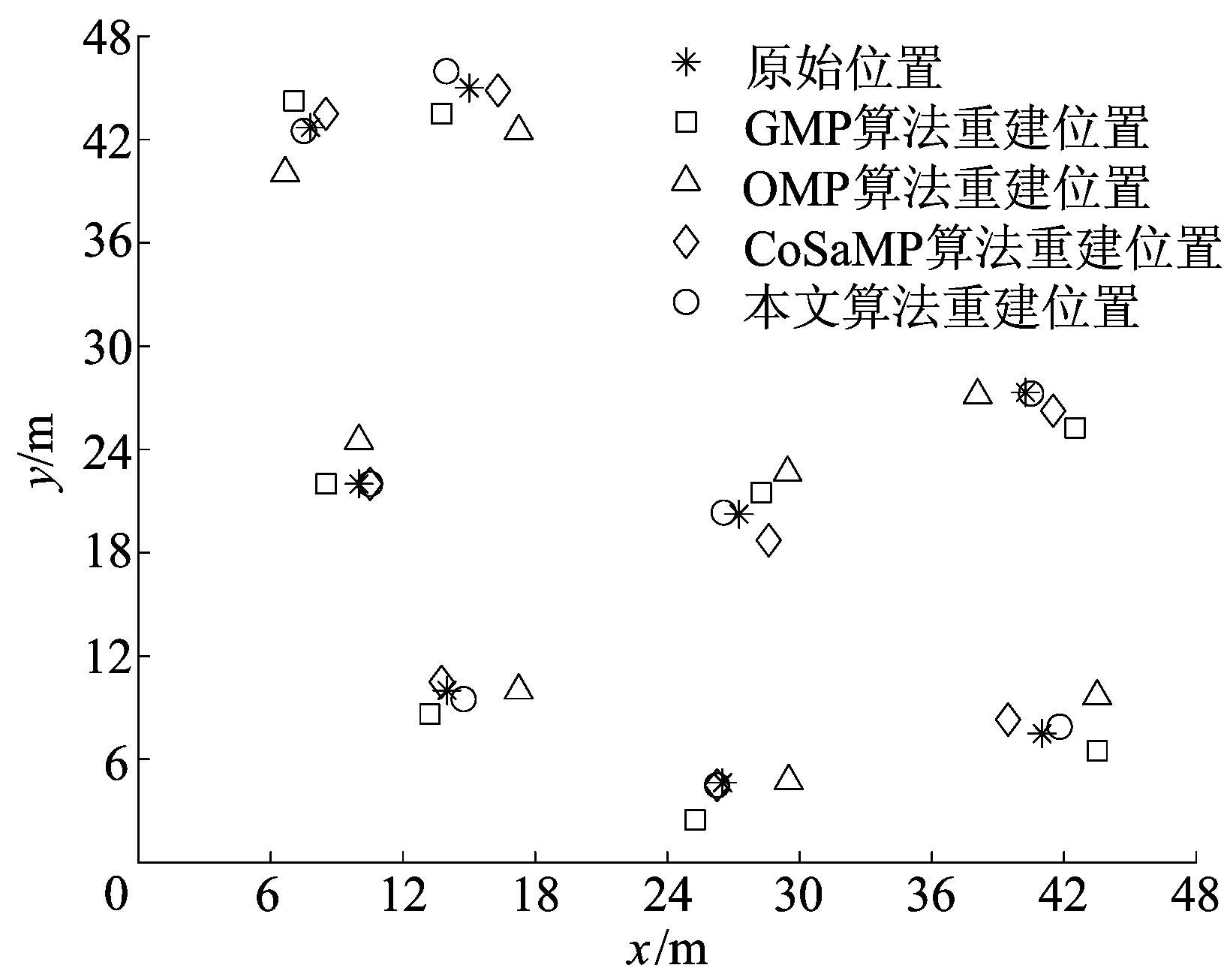
图4 4种算法定位结果对比

4种算法在K=8时不同信噪比下的定位成功率如图5所示。随着信噪比的上升,节点接收到的信号强度准确性显著上升,4种算法的定位成功率均呈上升的趋势,当信噪比达到一定程度时,定位成功率趋于稳定。在噪声为5 dB时,OMP算法、GMP算法以及CoSaMP算法定位成功率分别为0.15、0.24、0.42,大多数目标无法正确定位,本文算法的定位成功率为0.61,相比OMP算法、GMP算法以及CoSaMP算法,相应提高3倍、1.5倍以及45%,在噪声较大的条件下依然能够保持较高的定位成功率,表明本文算法抗噪性能较好,鲁棒性较强。

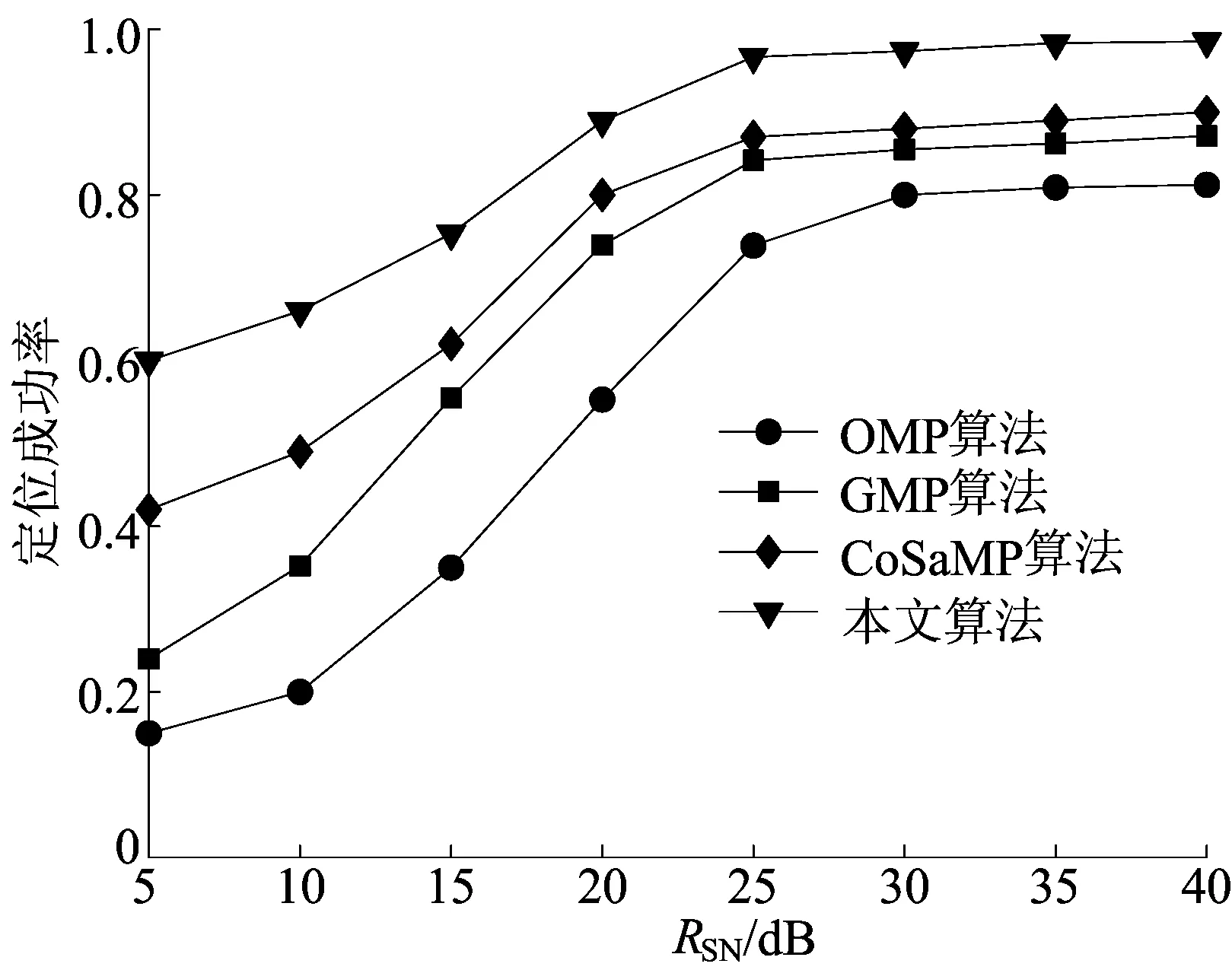
图5 4种算法在不同信噪比下的定位成功率对比

当K=8时，4种算法的定位误差随信噪比的变化如图6所示。在信噪比为5 dB时, OMP算法、GMP算法、CoSaMP算法定位误差分别为6.02、5.13、4.37 m,本文算法的定位误差为2.31 m,远小于对比算法。随着信噪比的增加,4种算法的定位误差逐渐减小,当信噪比达到20 dB之后4种算法的定位误差减小趋势较缓,当信噪比为40 dB时,本文算法的定位误差为0.66 m左右,OMP算法、GMP算法和CoSaMP算法定位误差分别为1.72、1.24、1.04 m。由此看出,在相同噪声的条件下,本文算法的抗噪性能要优于对比算法,鲁棒性较强。

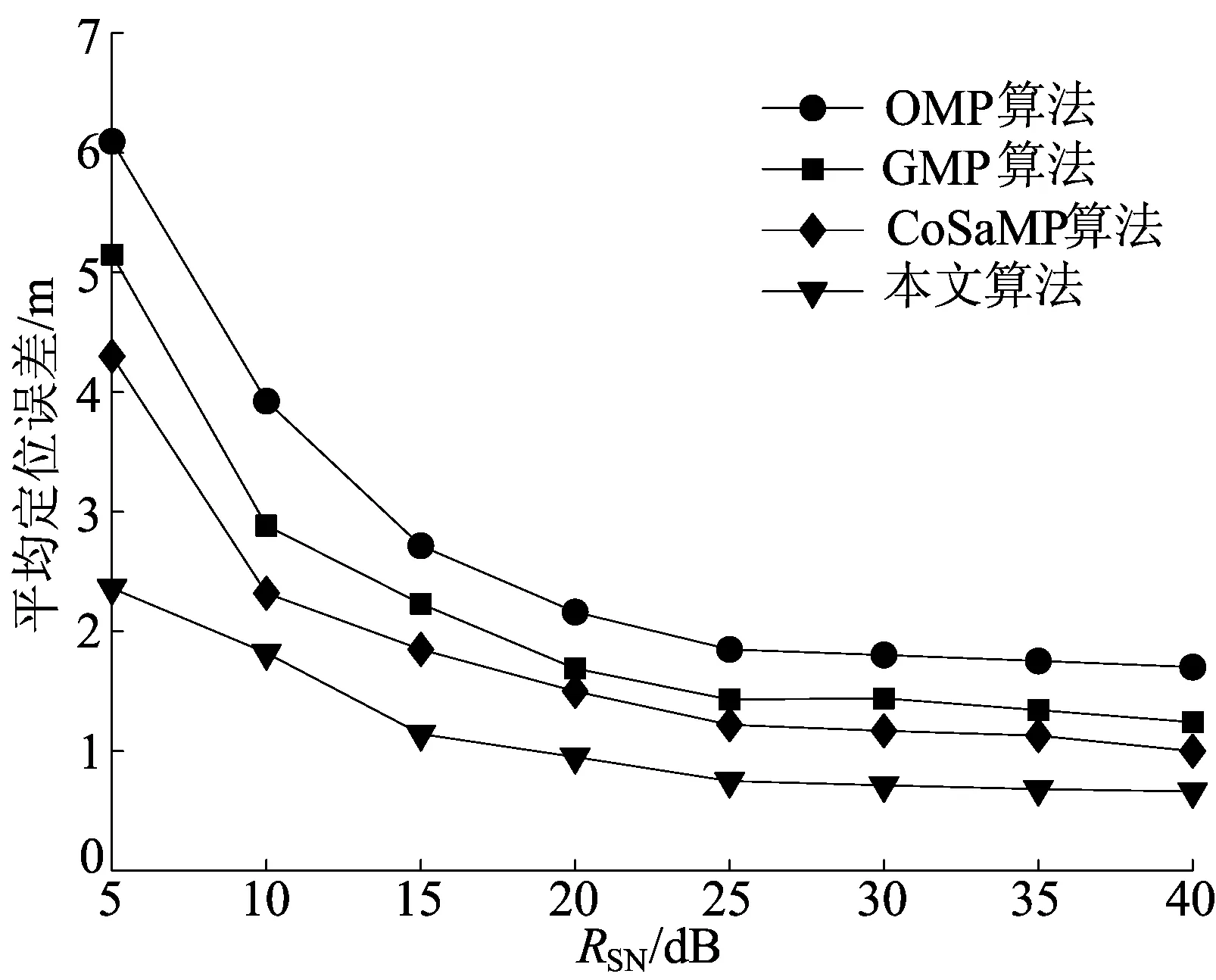
图6 4种算法在不同信噪比下的定位误差对比

当RSN=25 dB时,4种算法的定位误差随着目标数目变化情况如图7所示。从图7可以看出，随着目标数的增多,4种算法定位误差增大,这是由于压缩感知算法的重建性能随着稀疏度的增加而下降。在相同目标数下,本文算法的定位误差始终小于其他算法。从图7中还可以看出，本文算法随着目标数的增加定位误差上升较慢,其他算法误差增长较快。当目标数为20时,本文算法定位误差为1.05 m,对比3种算法误差均超过2 m,进一步表明本文算法受目标数影响较小,适应性更强。

图7 4种算法在不同目标数目的定位误差对比

4种算法在K=8时在不同信噪比下的定位时间如图8所示。在RSN=25 dB时,OMP算法、CoSaMP算法、GMP算法以及本文算法的平均定位时间分别为0.002 71、0.034 50、0.042 60、0.030 90 s。OMP算法定位时间短,但定位精度远远小于其他算法。GMP算法每次迭代需要遍历所有的网格找到使残差衰减最大的网格位置作为目标位置,计算量较大,定位时间较长。本文算法引入bounding-box算法减小定位区域有效地降低测量矩阵的维数,相较于GMP算法以及CoSaMP算法,本文算法的运算量分别减少29.6%、18.7%,因此具有更低的定位时延。

图8 4种算法在不同信噪比下的定位时间对比

3.2 实物验证

为验证算法的定位性能,在空旷的操场设置相应的物理实验。实验区域大小为6 m×6 m,使用CC2530芯片作为无线信号发射节点,CC2530芯片的发射频率为2 405.0～2 583.5 MHz,节点功率为-25 dBm,利用安捷伦频谱仪E440测量接受信号强度。在中心放置CC2530芯片,每隔0.5 m使用安捷伦频谱仪测量接收信号强度,每个点测量20次进行卡尔曼滤波处理,过滤数量小、幅度大的噪声,由此可以近似获得(1)式所示的接受信号强度模型的参数,其中P0≈-31 dBm,n≈2.1。将CC2530芯片放置在定位区域内,在定位区域内设立9个观测点,利用安捷伦频谱仪测出观测点的接收信号强度,每个位置测量20次进行卡尔曼滤波处理从而得到测量向量。将接受信号强度小于-40 dBm视为节点的通信范围之外,由此得到通信半径。利用接收信号强度大于-40 dBm的观测点计算出估计区域,划分网格,根据接收信号强度模型构建测量矩阵,然后利用本文算法进行压缩感知位置估计。传统压缩感知算法将网格划分为6×6的网格,即网格步长为1 m,同样用安捷伦频谱仪测得9个观测点的接收信号强度值获取测量向量,然后根据信号接受强度模型获得基于接收信号强度模型的观测字典,利用GMP算法、CoSaMP算法、OMP算法进行定位。改变CC2530芯片的位置,重复上述实验得到3个未知节点的定位数据，见表2所列。

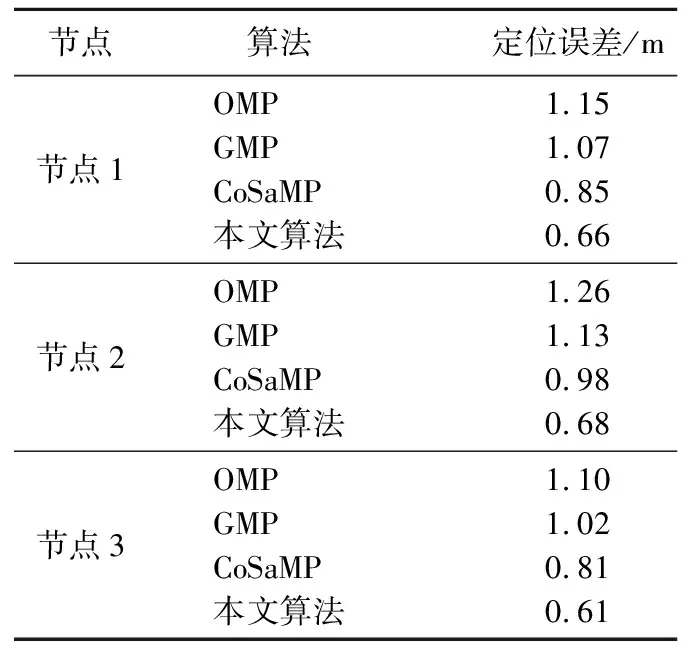
表2 定位实验结果对比

对3个节点的误差取平均值可以得到OMP算法、GMP算法、CoSaMP算法以及本文算法的平均定位误差分别为1.13、1.07、0.88、0.65 m,本文算法定位精度最高,相较OMP算法、GMP算法、CoSaMP算法分别提升了41.7%、39.3%、26.14%。实际定位中受到环境因素的干扰,接收信号强度测量不准确,影响压缩感知重构精度,本文对接收信号强度进行卡尔曼滤波能够有效过滤掉噪声从而提高压缩感知重建精度,进而减小定位误差。

4 结 论

本文在分析已有压缩感知算法不足的基础上,提出了一种优化压缩感知算法。首先利用卡尔曼滤波对传感器节点采集的接收信号强度值过滤噪声信号提高测量精度;然后引入bounding-box算法进行区域锁定,有效减小定位区域从而降低压缩感知测量矩阵的维数,减小运算量。针对压缩采样匹配追踪算法候选集原子冗余度大,支撑集选择精度低的问题,本文采取原子相关度阈值的控制策略对候选集中的原子进行二次筛选,并在支撑集保留相关系数较大的原子,提高压缩感知重建精度。实验表明,本文算法的定位速度较传统的GMP算法以及CoSaMP算法有所提升,在不同的目标数以及不同噪声下的定位精度均优于对比算法,具有更好的抗噪性和鲁棒性。