变胞机器人腿部结构轻量化设计
2023-01-05阮小栋
刘 俊, 阮小栋, 李 睿
(合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)
变胞机器人是一种能用于多种路况的可变形机构,能在结构路面以汽车态轮式行驶,在非结构路面可变形为两足机器人(类人态)以轮足式行走。变胞机器人主要通过折叠腿等变胞机构实现汽车态与类人态间的变形,而所谓变胞机构[1]是由戴建生教授在1998年提出来的一种新型机构,这种机构能够根据工作环境的改变而改变自身的拓扑结构、功能及自由度。
为了降低变胞机器人变形及行走(行驶)时的能量消耗,有必要在有限元理论基础上运用优化方法对变胞机器人的腿部机构进行轻量化设计。在优化设计研究方面,文献[2]将均匀化方法应用于多工况条件下的结构拓扑和形状优化;在多目标优化方面;文献[3]提出了最优拉丁超立方法来进行实验设计,最优拉丁超立方的提出克服了全因子法选点过多和拉丁超立方选点不均的缺点;文献[4-7]通过不同的方式对近似模型的精度进行评价,以确保后续研究中所获得的结果与真实情况一致;文献[8]提出了NSGA-II方法,该方法在寻优中能够快速准确地获得全局最优点;文献[9]提出了最小距离选择法,能够从Pareto前沿点中选择一个中庸的解。
本文基于设计的变胞机器人腿部结构,通过ADAMS仿真获得变胞机器人关键点处载荷谱,并利用仿真结果对腿部各构件进行多目标优化,实现变胞机器人腿部的轻量化设计,最后对优化后的构件进行仿真及试验验证。
1 变胞机器人结构及建模仿真
1.1 变胞机器人结构及构态分析
变胞机器人的整体结构复杂,包括车轮、转向总成、制动总成、悬架总成、举升机构、变质心机构、车架以及腿部机构等,其中腿部机构是最复杂的部分,也是本文的研究对象。腿部机构中左、右腿均包含6个自由度,分别位于车底板与髋关节连接处、髋关节与十字筒连接处、十字筒与大腿连接处、大腿与小腿连接处、小腿与踝关节连接处、踝关节与脚连接处。腿部完全折叠状态如图1所示。
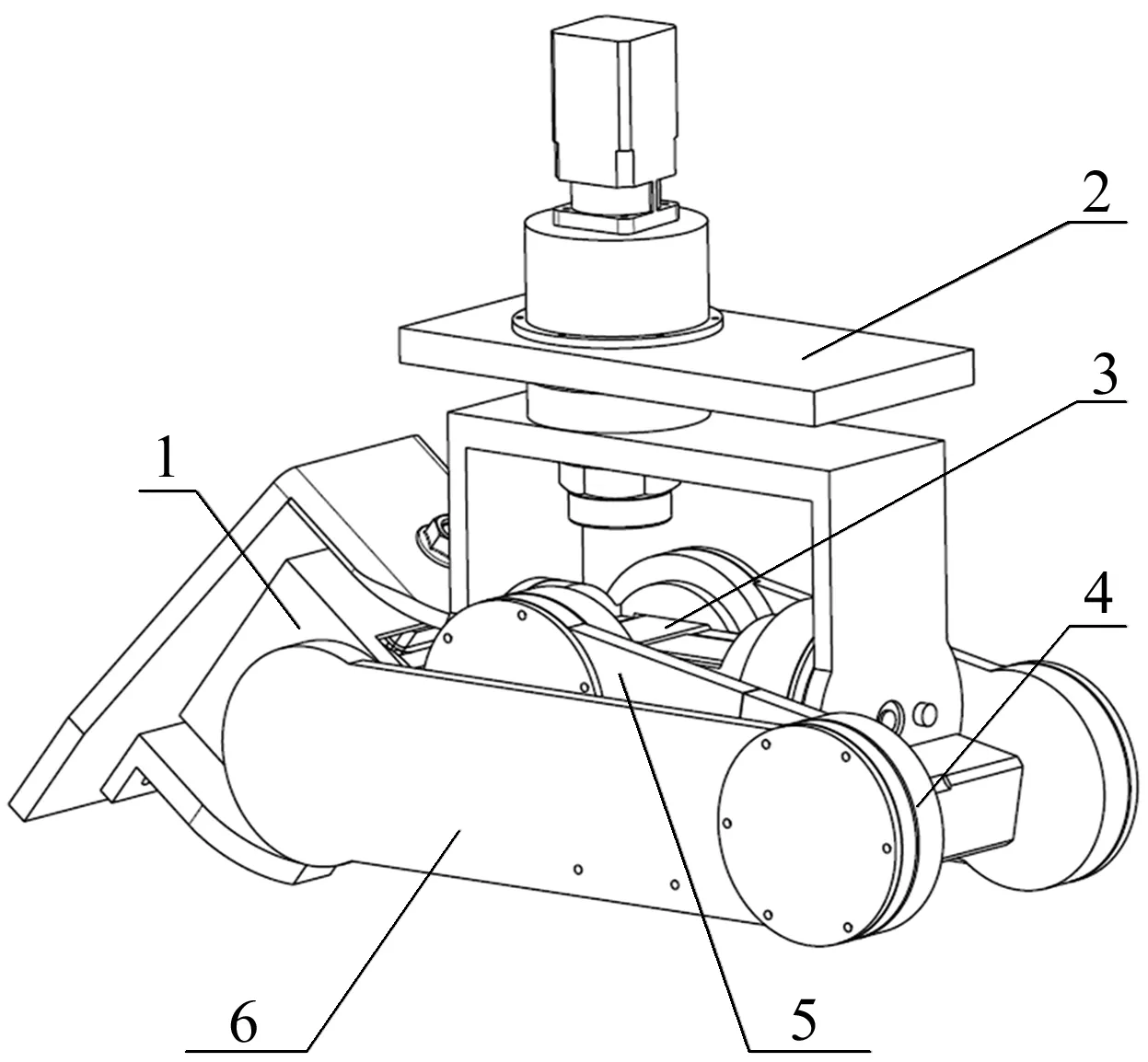
1.踝关节机构 2.车底板 3.髋关节机构 4.膝关节结构 5.大腿构件 6.小腿构件
为了实现变胞机器人在结构路面上的行驶与非结构路面上站立行走,要求其能够在汽车态与类人态之间快速、平稳地重构。变胞机器人由汽车态向类人态重构的过程共分为4种构态,分别为汽车态、支撑态、举升态、类人态。变胞机器人的4种构态如图2所示。
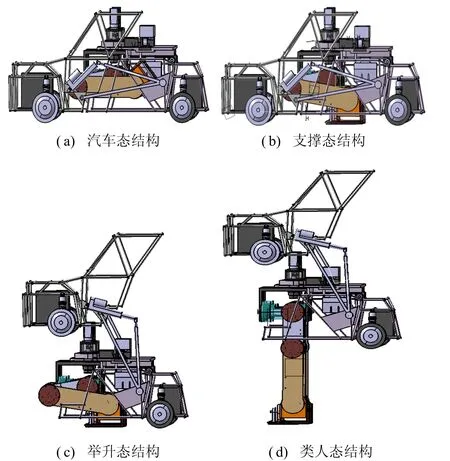
图2 变胞机器人重构构态
变胞机器人从汽车态到支撑态的过程是腿部由完全折叠到脚部与地面接触的过程,在整个过程中腿部各构件只承受自身重力,受力较小,可以不予考虑。因此使用ADAMS仿真时,获取的是从支撑态开始重构为类人态这一过程的载荷谱。
1.2 多体动力学建模
变胞机器人的运动工况包括汽车态行驶、类人态行走以及汽车态与类人态间的重构。其中,在汽车态重构为类人态的过程中,腿部机构受力最大,因此需要在ADAMS中建立变胞机器人的虚拟样机,通过仿真求取汽车态向类人态重构时腿部的载荷谱。在进行仿真之前,需要对变胞机器人的重构时间进行规划,正常的重构过程中举升所占时间为15 s,起立为18 s。而为了提高轻量化设计的可靠性,在后续仿真求取载荷谱时,通过缩短正常重构时间使得重构时腿部机构承受比正常重构时高得多的工作载荷(2.5~3.0倍正常重构时的工作载荷),并要求在该载荷下进行轻量化设计。
快速重构的时间规划是举升6 s、起立6 s,2种时间序列见表1所列。

表1 重构过程时间序列
因为在CATIA中已经建立变胞机器人的三维模型,所以首先要将CATIA中建立的三维模型导入ADAMS中,然后在ADAMS中对模型进行连接和运动的设置。在举升过程中,举升机构类似于平面四杆机构有2个驱动源,步进电机提供旋转运动,电动推杆提供平移运动,同时在四杆机构中的4个铰链处添加4个转动副;在立起过程中,变胞机器人腿部髋关节、膝关节及踝关节共有6个自由度,在这6处均添加转动副,并在每一处转动副添加1个旋转运动。为获得脚底板处受力,在脚底板与大地之间建立接触。最后建立的ADAMS动力学模型如图3所示。

图3 ADAMS多体动力学模型
1.3 仿真求取载荷谱
对建立的ADAMS多体动力学模型进行支撑态至类人态的快速重构仿真,仿真后获得关键部位的载荷谱。在重构过程中,Z向载荷最大,而X向及Y向载荷非常小,因此在分析时不予考虑。通过仿真得到车底板与髋连接处、髋与十字筒连接处、十字筒与大腿连接处、大腿与小腿连接处、小腿与踝连接处、踝与脚连接处、脚与地面接触处各关键部位Z向受力曲线,以小腿与踝连接处Z向受力曲线为例,如图4所示。
从图4可以看出:0~1 s,整个变胞机器人处于静止状态,所有受力点载荷大小基本不变,约为整车重量的1/2;1~6 s的举升过程中,由于受内部惯性力影响,载荷有轻微波动,呈现正弦曲线样式;在第6 秒举升过程结束时,载荷大小恢复为初始值;在6~12 s的起立过程中,其载荷变化与举升过程类似。起立过程结束后,载荷大小恢复为初始值。
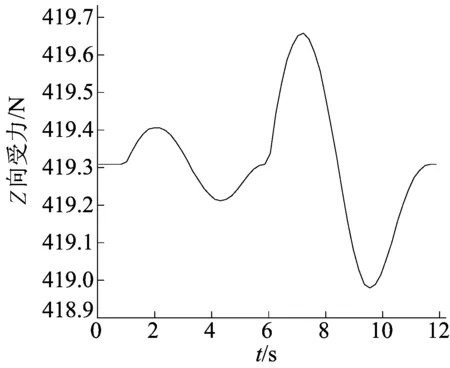
图4 小腿与踝连接处Z向受力曲线
整个仿真过程中,所有腿部关节所受扭矩最大处为小腿与脚踝连接处,其扭矩变化曲线如图5所示。
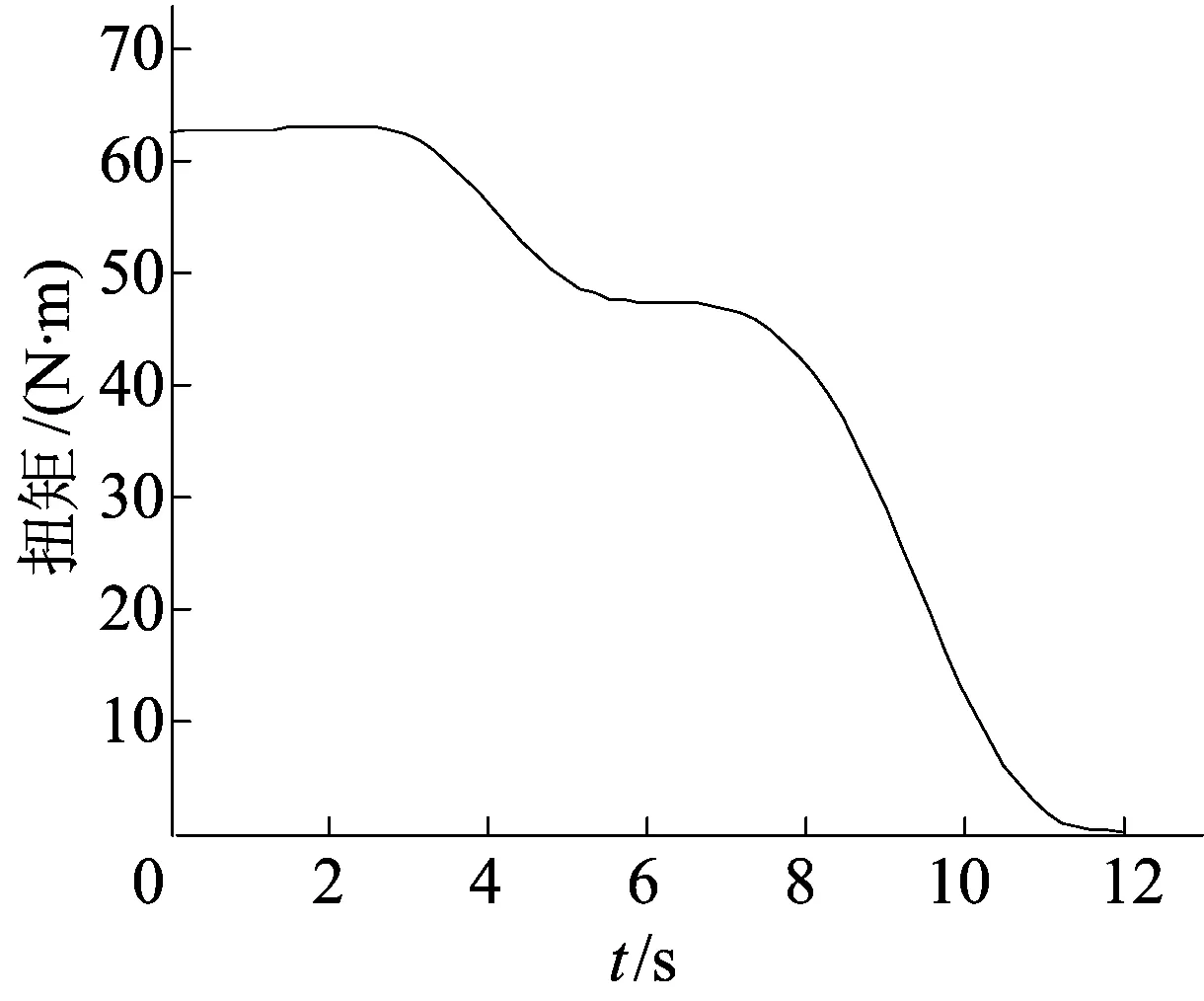
图5 起立过程中最大扭矩变化曲线
从图5可以看出,重构过程中所受最大扭矩不超过65 N·m。在重构过程开始时,腿部完全折叠,小腿与地面之间的夹角很小,重力在膝关节处垂直于小腿的分力最大,而此时小腿充当杆臂,因此初始时刻所受扭矩最大;1~6 s的举升过程中,扭矩逐渐减小,这是因为举升过程中前车身被举升起来,前车身质心发生变化,逐渐靠近小腿与踝连接处,质心与连接处距离逐渐减小,力臂逐渐缩短,所以扭矩逐渐减小;6~12 s是起立过程,在此过程中扭矩进一步减小,并在重构结束前趋近于0,这是因为在起立过程中腿部伸直,大小腿与地面夹角逐渐变为直角,所以扭矩逐渐趋近于0。
2 基于多目标优化的轻量化设计
2.1 变胞机器人腿部有限元建模
将CATIA中建立的腿部机构三维模型导入Hypermesh,在Hypermesh中对三维模型进行清理、简化和网格划分。本文将腿部各构件划分为四边形网格,并将网格尺寸选择为5 mm。在网格划分完成后,对网格赋予材料属性,其中变胞机器人采用全铝合金结构,铝合金的许用应力为112 MPa。
根据实际工况和设计要求,对变胞机器人腿部结构添加载荷,其中力和扭矩已经通过ADAMS仿真求得。但由于在Hypermesh仿真分析时,添加随时间历程变化的载荷会使计算过于复杂,为降低计算量,本文添加的是大小确定的固定载荷。同时为了提高优化设计的可靠性,在添加载荷时,将ADAMS中变胞机器人快速重构仿真得到的载荷最大值作为添加到有限元模型中的载荷,并进行计算。
2.2 试验设计
在进行多目标优化时,为了不增大计算负荷,同时又能保证计算精度,试验设计使用最优拉丁超立方采样法。因为腿部各构件均为薄壁结构,所以在对髋、大腿、小腿、踝和脚底板5个腿部构件进行试验变量设计时,将壁厚选定为设计变量,构件有限元类型划分为壳单元,这既能保证仿真优化的准确性,又能极大地提高工作效率。
腿部各构件变量设计如图6所示,其变量数量和采样点数量见表2所列。

图6 腿部各部件变量展示
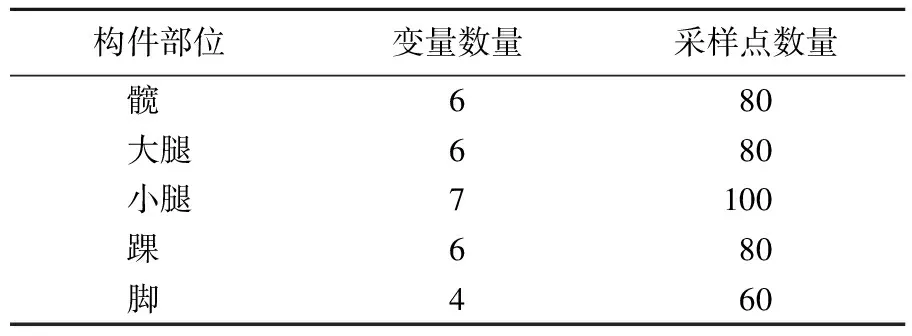
表2 构件试验设计变量及采样点数量
变胞机器人腿部构件均采用铝合金加工制作,具有重量轻、结构强度高的特点,因此将变量设计范围设定为2~8 mm。
优化目标需根据构件的实际性能确定。为了提高腿部的抗外在负荷能力,将构件所受应力作为一项优化目标。此外,为降低变胞机器人的能耗和生产成本,需要尽可能地降低构件的质量,将构件的质量也设定为一项优化目标。因此,优化目标分别为质量和应力。
优化变量和优化目标确定后,需在Isight中进行试验设计,试验设计完成后,按照试验设计的结果,对每一个采样点进行有限元仿真,并记录每次仿真的结果。
2.3 模型近似及精度评估
采用最优拉丁超立方试验设计方法对设计变量进行抽样,同时对比不同模型的误差及模拟精准度,最终选择响应面法近似模型。
由于在采样过程中有很大范围是没有进行采样的,近似模型建立完成后,必须验证其精度,以确保近似模型能够最大程度地还原真实模型,保证后续结果的可靠性。在评估过程中,将决定系数R2作为评估标准,R2给出了近似模型的整体拟合优度。R2的数学表达式[10]如下:
(1)
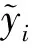
应用四次响应面法建立的各个部件近似模型评估结果见表3所列。
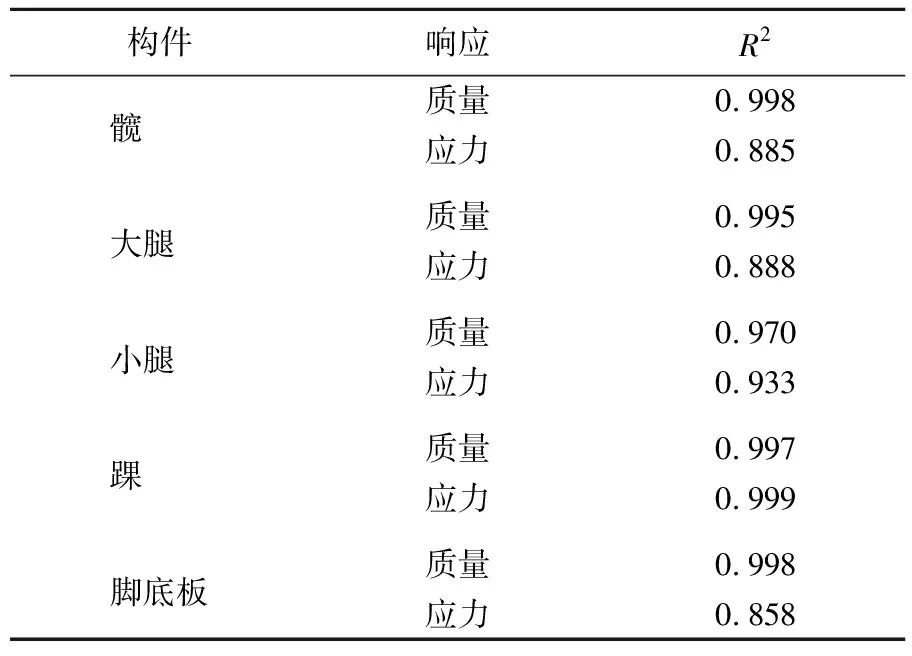
表3 腿部各构件评估结果
从表3可以看出,用四次响应面法建立的近似模型误差较小,决定系数均大于0.85,满足要求。
因此,后续优化过程可以在以上模型的基础上进行。
2.4 NSGAII多目标优化
目前多目标优化算法有很多种,各种多目标优化算法都能够在每一次运算中得到多个Pareto前沿解,并最终获得一系列前沿解[11-13]。在众多算法中,非支配排序遗传算法(NSGA-II)因具有多样性保证策略、拥挤度计算策略和快速非支配策略,且能够准确寻找到Pareto前沿解,已经成为目前应用最广的一种优化算法。NSGA-II算法寻优的基本步骤如下:
(1)对算法初始化,并产生规模为N的随机种群。
(2)对步骤(1)产生的随机种群进行非支配排序后,通过传统遗传算法的选择、交叉、变异获得第1代子种群。
(3)从第2代开始,将父种群与子种群相互融合并进行非支配排序,同时对每个非支配层中的个体进行拥挤度计算,从而挑选出合适的个体组成新一代父种群。
(4)使用传统遗传算法的相应机制获得新一代子种群,重复上述迭代步骤,直至满足NSGA-II算法的终止条件时停止迭代,输出所获得的Pareto前沿。
由于NSGA-II算法迭代次数过少将会导致部分区域遗漏,使得计算结果不准确,而迭代次数过多也会使计算时间过长,降低效率。因此设置迭代次数为115次,并设置质量和应力的目标为最小。
优化完成后,导出腿部各构件Pareto前沿,如图7所示。
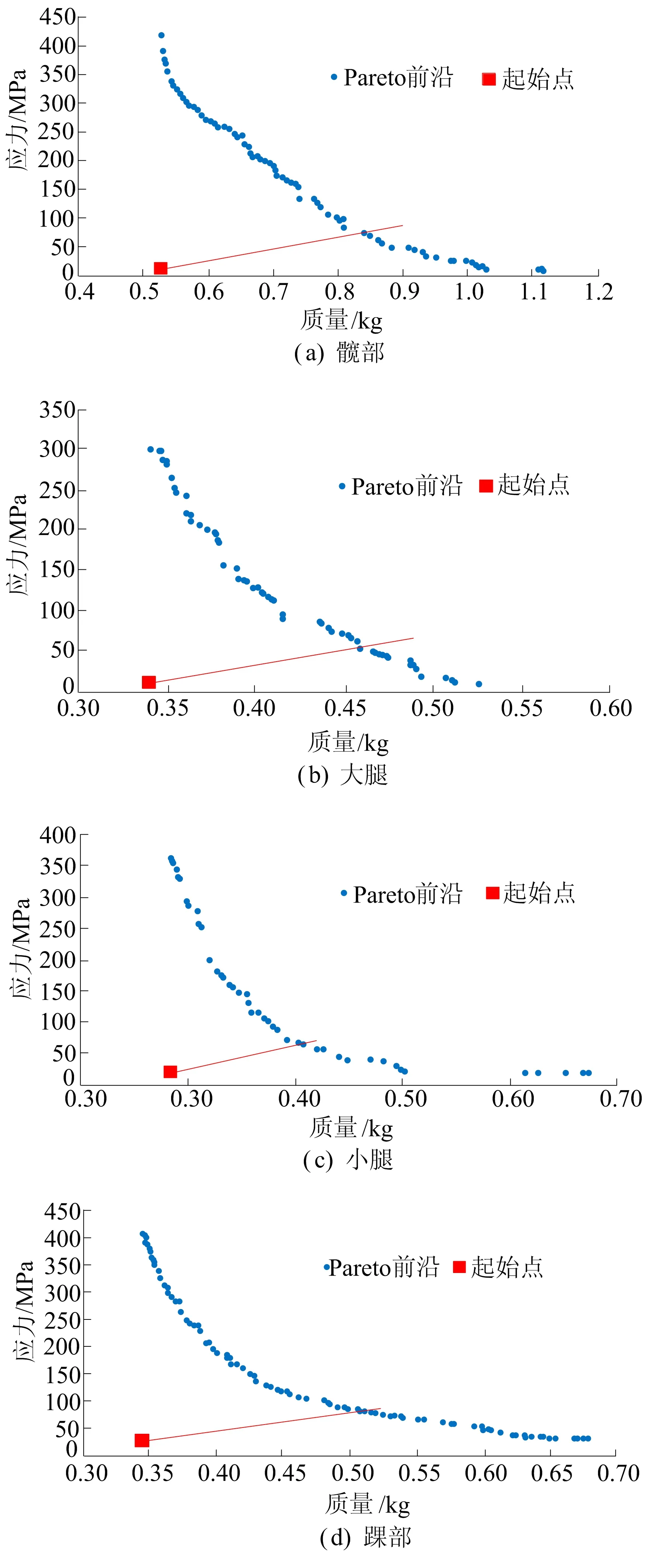
图7 腿部各构件Pareto前沿点图
2.5 权重选择法
经过不断地迭代,可以得到Pareto前沿,然而Pareto前沿是针对优化目标的很多个非劣解的集合,如何从Pareto前沿中选取最理想的点,成为接下来需要解决的问题。目前选点方法很少,比较常用的有最小距离选择法和公差分配最优解选择法。在绝大多数情况下,设计时选用的点都是工程师根据自己的工程经验和对优化目标的重要程度选择的,这样的方式虽具有一定的科学依据,但过程非常不规范,而且很难在一个行业内达成共识。
本文针对目前选点不规范的问题,提出了一种规范的方法,即权重选择法。该方法引入了权重的概念,通过将更重要的目标设定为大权重,将相对次要的目标设置为小权重,使最终的选点倾向于更重要的优化目标。
权重选择法的数学模型如下:
Y=(-1)αaβKX+b
(2)
(3)
(4)
b=起始点纵坐标-
(-1)αaβK×起始点横坐标
(5)
其中:a为权重系数;K为修正系数;b为常数项;α、β为优化目标极值组合选择系数;X、Y分别对应所选优化目标的质量和应力。
(5)式中,起始点横坐标为Pareto前沿点中横坐标最小值,起始点纵坐标为Pareto前沿点中纵坐标最小值,该点也称为‘乌托邦’点。此外α、β的选择如下所述:若优化目标1与优化目标2取值均为最大值或均为最小值,则α=0,β=1;若优化目标1与优化目标2取值为最大最小或最小最大,则α=1,β=-1。由于优化目标质量和应力都要求最小,因此(5)式中,α=0,β=1。
所优化的腿部结构中强度的重要性要高于质量,因此,将质量权重定为1,应力权重定为3,则a=1/3。其余参数计算结果见表4所列。
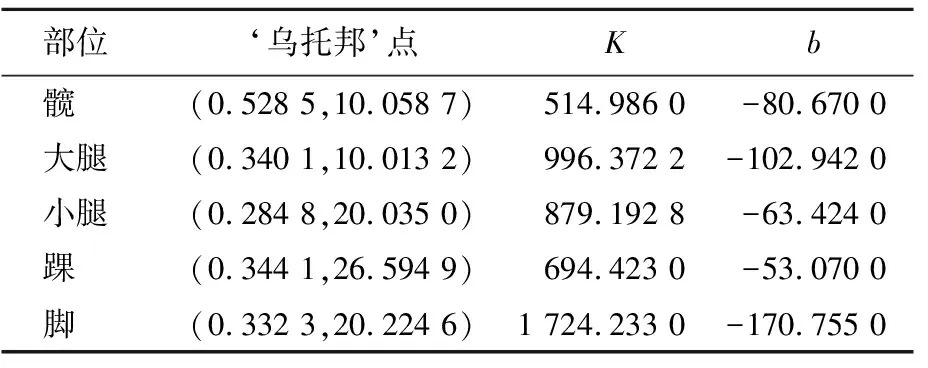
表4 权重选择法参数
在获得起始点坐标及K、b等参数后,将参数代入(2)式,得到一条直线,即图7中红色直线。
然后通过点到直线距离公式计算每个Pareto前沿点到直线的距离,计算完成后,将距离最小的点筛选出来,得到的最优解见表5所列。

表5 腿部各部位选点结果及距离
为了尽可能保证构件的工作可靠性,在设计时,一般选取的最优解点要低于材料屈服强度的80%。因为铝合金的屈服强度为140 MPa,所以选择的最优解必须小于112 MPa。
从表5可以看出,腿部各构件所选择的最优解均小于112 MPa,保证了各构件工作的可靠性。得到Pareto最优解后,需要按照最优解结果对构件重新建模。
3 仿真验证分析
对优化设计后的构件进行有限元分析,分析结果如图8所示。
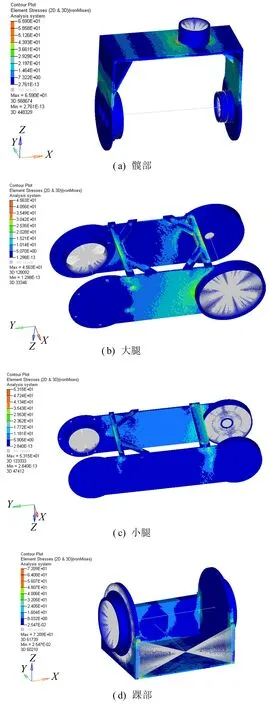
图8 优化后腿部各部件应力图
优化后各构件质量、应力最大值见表6所列。其中,误差表示为有限元分析值与近似模型预测值之间的误差。
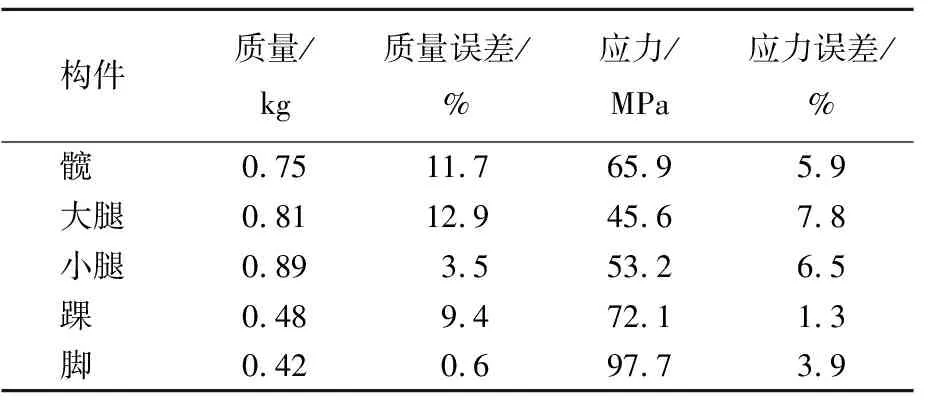
表6 优化后各构件的质量、应力和位移
从表6可以看出:无论是质量还是应力,误差均控制在较小的范围内,这也进一步验证了之前所建立的近似模型的准确性;同时优化后最大应力为97.7 MPa,满足强度要求。
优化前、后各构件质量见表7所列。
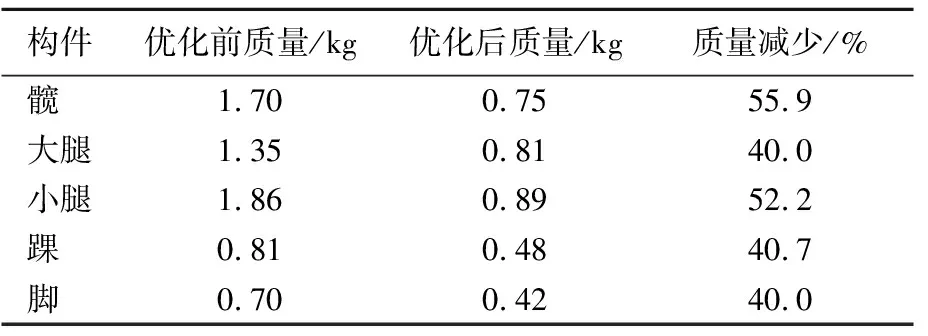
表7 腿部各构件优化前、后质量比较
从表7可以看出,优化前、后构件质量下降明显,这是因为优化前进行保守设计时的构件厚度很大,优化后构件质量出现大幅下降。在满足强度要求的前提下,大幅度降低了构件的质量,表明多目标优化效果明显,也进一步说明了本文提出的权重选择法是一种切实可行的方法。
4 变胞机器人的腿部应力测试
在由汽车态重构为类人态的过程中,对轻量化后的变胞机器人腿部机构的关键受力部位进行应力测试[14-15]。为了便于分析对比,该测试分正常重构和快速重构2种工况(与1.2节的仿真工况一致)。在测量腿部机构重构过程中的应力变化时,根据变胞机器人腿部机构的结构特点和仿真得到的静态强度应力云图,选取腿部结构中各组成部分的最大受力点作为试验测试点。在机器人腿部的相应位置按照实际受力方向进行应变片布置,应变片粘贴时先要将粘贴部位打磨抛光,用胶水均匀地涂附在粘贴表面,再将应变片按指定方向粘贴在测试点处,并在其上面覆盖一层聚氯乙烯薄膜,用手指顺着应变片的长度方向用力挤压,挤出应变片下面的气泡和多余的胶水,最后用手指压紧,直到应变片与测试部位紧密粘合为止。本文应力测试用到的应变片如图9所示。

图9 应变测量采用的应变片
将已经粘贴好应变片的变胞机器人放置在应力测试场地上,为了避免机器人在重构过程中可能会出现倾倒所带来的安全问题,试验时机器人通过2根绳索悬置在支撑架上,以保证试验过程中机构以及人员的安全,如图10所示。

图10 整车应力测试台架(左)和测试设备(右)
在重构过程中,变胞机器人质心和各关节处的电机扭矩均会发生变化,因此腿部各试验测试点处的载荷也会随之发生变化。在变化载荷作用下,腿部各部件将产生变形,应变片也随着部件的变形而产生弹性应变,应变通过电流信号进行检测并传送,由信号采集仪进行收集。应变片发生的是弹性应变,因此符合胡克定律的基本要求,即
σ=Eε
(6)
其中,E为弹性模量,整车材料铝合金一般取作7.2×104MPa。
应变信号通过采集仪收集后导入到计算机,在应力处理软件中进行分析处理,即可得到各试验点在重构过程中的最大应力输出,结果见表8所列。
从表8可以看出,通过静态加载最大载荷仿真得到的有限元分析值和实物进行快速重构时的实测值基本吻合,应力值最大误差为6.0%。误差的存在可能是由于实物状态和模型有一定的差异,且加载过程中也会发生一定的偏差。另外,从表8还可以看出,变胞机器人在快速重构过程中的实测值均明显大于正常重构过程中的实测值。这表明当重构时间缩短时,机构会承受一定的冲击载荷,造成整体应力值有增大的迹象。在5个测试点中,踝关节处测试点的应力最大,最大应力为99.9 MPa,但还是在所采用的材料铝合金许用应力范围内。
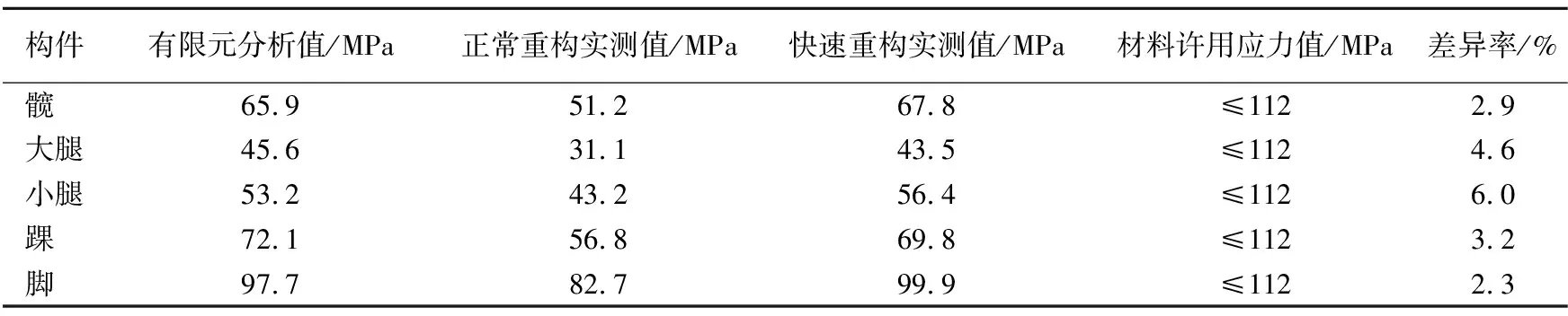
表8 各构件最大受力点处应力测试值与分析值对比
上述结果表示,本文所建立的有限元模型是较准确的,轻量化设计是有效且安全的。
5 结 论
(1)本文对变胞机器人腿部构件进行多目标优化,选取质量和应力作为优化目标,建立近似模型,并进行寻优,获得Pareto前沿。
(2)提出了一种新的最优解选择方法权重选择法。此方法是一种程式化的方法,可以根据优化目标的重要程度设置不同的权重系数,并通过计算从Pareto前沿中选取最优解。经仿真对比验证,此方法切实可行。
(3)所进行的腿部多目标优化是在第1轮保守设计的基础上进行的,因为最初设计的构件厚度很大,构件的所有厚度均需优化,所以本文并没有进行灵敏度分析,这也是优化完成后质量下降明显的原因。
(4)本文研究对象是一种新型的特种机器人,具有广泛的军民应用前景,该研究结果可以为后续的重构运动控制打下坚实的基础。
